Введение
В рамках неоклассической теории производства оптимальный размер производственного сегмента корпорации (предприятия акционерной формы собственности) – суммарная величина активов, включенных в этот сегмент, обеспечивающая максимальную эффективность затрат собственного и заемного капитала по критерию валового дохода с учетом сложившихся на момент принятия решения об объемах производства цен на готовую продукцию, факторы производства, ставок заемного финансирования, налогов и пр. Проблематика экономико-математического моделирования производственной сферы предприятия, функционирующего в изменчивой рыночной среде, достаточно полно представлена в трудах зарубежных [1, 2, 3, 4, 5, 6, 7, 8, 9] и отечественных исследователей [10, 11, 13], включая и работы авторов [13, 14, 15, 16].
В работах перечисленных авторов оптимальный размер производственного сегмента предприятия оценивается, однако, исключительно по критерию доходности производственной программы, включающей продукцию основного и вспомогательного производств. Однако, в условиях сегментации бизнеса по центрам ответственности, ставшей заметной особенностью современной организации производства, такой подход не может быть признан удовлетворительным. Производственный сегмент корпорации, как и любой другой центр ответственности (центр прибыли, затрат, инвестиций), кроме функции обеспечения доходности основной производственной деятельности, выполняет функции по организации ее финансирования, снабжения – сбыта продукции, эффективного использования основного и оборотного капитала и др. Очевидно, что учет в оценках валового дохода производственного сегмента предприятия объектов неосновной деятельности существенно отразится на основных его финансово-экономических и производственных показателях, включая и такие, как точка безубыточности и оптимальный размер выпуска.
Оптимальный размер предприятия в рамках неоклассической теории производства
В неоклассической теории производства [1, 2] аналитическое выражение оптимального по критерию доходности основной производственной деятельности объема производства получено для предприятия с однородной производственной функцией, являющейся:
– дважды непрерывно дифференцируемой в экономической области Ω (области задания);
– монотонно неубывающей и выпуклой вверх по каждому аргументу (в качестве аргумента выступает объем переменного или условно-постоянного ресурса – актива, включаемого в рабочий капитал (капитал производственного сегмента предприятия);
– однородной (степени r > 0):
f(αx1,..., αxi,..., αxI) = αrf(x1,…, xi,…, xI), (1)
где I – число учитывающих в модели предприятия активов; xi – объем i-го актива; α > 0, xi, αxi∈Ω.
В силу теоремы Эйлера об однородных функциях:
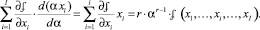 (2)
(2)
В точке 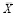 =
= 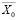 оптимального объема выпуска:
оптимального объема выпуска:
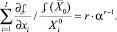 (3)
(3)
Учитывая, что левая часть соотношения (3) совпадает с суммарной эластичностью 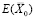 выпуска по факторам затрат (активов), запишем для α = 1:
выпуска по факторам затрат (активов), запишем для α = 1:
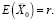 (4)
(4)
Обозначим выпуск (объем производства) предприятия переменной у:
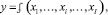 (5)
(5)
а валовые (переменные плюс условно-постоянные) затраты на объем выпуска у – через с(у). Тогда соотношение 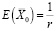 можно записать в виде:
можно записать в виде:
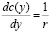 , (4`)
, (4`)
откуда получим следующее выражение для функции полных затрат на объем производства, равный у:
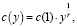 (6)
(6)
где с(1) – удельные валовые затраты (затраты в расчете на единичный объем производства).
Пусть p0 – валовый удельный доход для произведенной в производственном сегменте предприятия и реализованной продукции. Если ввести в рассмотрение функцию прибыли предприятия:
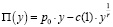 , (7)
, (7)
то оптимальный yопт объем производства для предприятия с неоклассической производственной функцией можно получить из условия экстремума для функции прибыли:
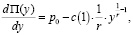 (8)
(8)
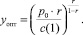 (9)
(9)
Комментарий. Для r > 1 объем производства, устанавливаемый на основе выражения (9), – точка минимума функционала (7). Для r > 1 – точка максимума.
В реальной производственной практике наиболее распространенным является второй случай: переменные и условно-постоянные затраты растут быстрее выпуска по причине нарастания косвенных затрат на входе и выходе производственного сегмента и нарастания трансакционных затрат сбыта и реализации.
Таким образом, оптимальный объем уопт производства для предприятия с неоклассической производственной функцией степени однородности, меньшей 1, задается выражением (8).
В общем случае (функция «затраты-выпуск» не обязательно является однородной) оптимальный размер производственного сегмента предприятия с учетом рыночного риска производственной программы может быть определен на основе следующей модели:
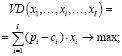 (10)
(10)
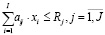 ; (11)
; (11)
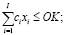 (12)
(12)
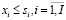 ; (13)
; (13)
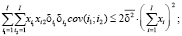 (14)
(14)
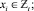
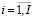 , (15)
, (15)
где VD – валовый доход при выборе производственной программы, задаваемой вектором 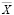 ; pi,, ci – средние за период наблюдения и принимаемые в расчетах за актуальные соответственно, рыночная цена и удельные производственные затраты по i – му изделию производственной программы; J – число технологических операций, используемых в производственном сегменте предприятия; aij – технологическая фондоемкость производства i-го изделия на j-й операции; Rj – эффективное время работы технологического оборудования на j-й операции; OK – оборотный капитал (текущие активы производственного сегмента предприятия); Si – рыночные спрос на i-е изделие производственной программы предприятия; δi – дисперсия доходности i-го вида продукции за период наблюдения; cov(i1; i2) – ковариация доходностей продукции с индексами i1 и i2 (за период наблюдения); δ – пороговое значение риска производственной программы принимаемого собственниками и менеджментом.
; pi,, ci – средние за период наблюдения и принимаемые в расчетах за актуальные соответственно, рыночная цена и удельные производственные затраты по i – му изделию производственной программы; J – число технологических операций, используемых в производственном сегменте предприятия; aij – технологическая фондоемкость производства i-го изделия на j-й операции; Rj – эффективное время работы технологического оборудования на j-й операции; OK – оборотный капитал (текущие активы производственного сегмента предприятия); Si – рыночные спрос на i-е изделие производственной программы предприятия; δi – дисперсия доходности i-го вида продукции за период наблюдения; cov(i1; i2) – ковариация доходностей продукции с индексами i1 и i2 (за период наблюдения); δ – пороговое значение риска производственной программы принимаемого собственниками и менеджментом.
Экзогенные (неуправляемые) параметры модели Pi, Ci, Si определяются рыночной конъюнктурой. Эндогенными (управляемыми) параметрами являются: эффективное время работы 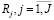 основного и вспомогательного оборудования на технологических позициях, OK – оборотный капитал производственного сегмента предприятия, авансируемый в покрытие затрат;
основного и вспомогательного оборудования на технологических позициях, OK – оборотный капитал производственного сегмента предприятия, авансируемый в покрытие затрат; 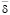 – предельный риск производственной программы.
– предельный риск производственной программы.
Если 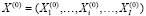 – оптимальное решение нелинейной целочисленной задачи (10) – (15), то оптимальные размер производственного сегмента предприятия определим по формуле:
– оптимальное решение нелинейной целочисленной задачи (10) – (15), то оптимальные размер производственного сегмента предприятия определим по формуле:
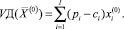 (16)
(16)
Учитывая выпуклость критерия (10) и ограничений (11), (12), (14), можно утверждать о наличии однозначной зависимости между оптимальным решением модели (10) – (15) и вектором (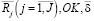 ) регулируемых параметров. А именно, если
) регулируемых параметров. А именно, если  – двойственные оценки соответственно ограничений (11), (12), (14), то оптимальные размер
– двойственные оценки соответственно ограничений (11), (12), (14), то оптимальные размер 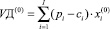 производственного сегмента предприятия соответствует значению функционала:
производственного сегмента предприятия соответствует значению функционала:
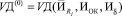 , (17)
, (17)
связывающего оптимальное решение модели (10) – (15) с вектором двойственных оценок регулируемых параметров.
Концепция и теоретические положения задачи выбора оптимального варианта производственной деятельности и размера производственного сегмента предприятия
Выше рассмотрены модели определения оптимального объема производства предприятия, функция «затраты-выпуск» которого корректно описывается соотношениями неоклассической теории производства или может быть получена на основе двойственных оценок регулируемых и нерегулируемых параметров внутренней (производственно-технологической) и внешней (рыночной) сред предприятия.
Важной особенностью этих моделей является их сугубо «производственная» направленность, в рамках которой производственный сегмент предприятия представляется классическим «черным ящиком» [15], на вход которого поступают производственные ресурс, а на выходе реализуется конечный продукт, стоимостная оценка которого (разница рыночной цены реализации и затрат в цепочке «снабжение-производство-сбыт») учитывается в финансовом результате основной производственной деятельности предприятия.
В реальной практике функционирующего в условиях рыночной экономики хозяйствующего субъекта деятельность его производственного сегмента не ограничивается только собственно выпуском продукции традиционного или инновационного ассортиментов, но включает и объекты внепроизводственной деятельности: сдача/взятие в аренду эксплуатационных и производственных мощностей, управление финансовыми активами и др. виды деятельности, приносящие доход. Учет операций внепроизводственной деятельности в оценках «рыночной» мощности производственного сегмента предприятия существенно отражается на результатах моделирования и на стоимостной оценке его оптимального размера.
Ниже рассмотрим формальную постановку и математическую модель определения оптимального размера производственного сегмента предприятия в условиях изменчивых товарных и финансовых рынков, параметры которых составляют экзогенную часть переменных.
Отметим, что модели производственной сферы предприятия можно рассматривать и в статическом (для выбранного временного интервала) и в динамическом (для последовательности временных интервалов) вариантах, которые существенно отличаются критериями и составом ограничений [12].
Остановимся на более простом статическом варианте модели с критерием на максимум валового дохода производственного сегмента предприятия, производственно-технологическими, финансово-ресурсными и рыночными ограничениями, характеризующими условия основной и внепроизводственной деятельности предприятия.
Формальная постановка задачи и статичный вариант модели определения оптимального размера производственного сегмента предприятия
Введем следующие обозначения для параметров и переменных модели определения оптимального размера предприятия (для упрощения восприятия интервал планирования t будем считать присутствующим в этих обозначениях):
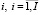 , индекс производимой продукции;
, индекс производимой продукции;
xi – планируемый объем производства i-того вида продукции;
pri(xi) – цена реализации единицы i-го вида продукции в объеме xi (в общем случае нелинейная функция объема реализации);
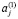 – стоимость эксплуатации и затрат на восстановление изношенной части j-го постоянного актива в основных активах (рабочем капитале) предприятия:
– стоимость эксплуатации и затрат на восстановление изношенной части j-го постоянного актива в основных активах (рабочем капитале) предприятия:
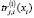 – эффективная нагрузка на j-й постоянный актив в рабочем капитале предприятия при производстве единицы i-го вида продукции в объеме xi (в общем случае нелинейная функция объема производства);
– эффективная нагрузка на j-й постоянный актив в рабочем капитале предприятия при производстве единицы i-го вида продукции в объеме xi (в общем случае нелинейная функция объема производства);
J1 – число составляющих постоянных активов, учитываемых в оценках себестоимости производимой продукции;
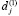 – средняя плата в расчете на единиц j-го постоянного актива, сдаваемого в аренду;
– средняя плата в расчете на единиц j-го постоянного актива, сдаваемого в аренду;
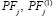 – соответственно, общая величина j-го постоянного актива в рабочем капитале предприятия и оставшаяся после сдачи в аренду часть эксплуатационных и производственных мощностей, используемая при производстве изделий из номенклатурного перечня предприятия;
– соответственно, общая величина j-го постоянного актива в рабочем капитале предприятия и оставшаяся после сдачи в аренду часть эксплуатационных и производственных мощностей, используемая при производстве изделий из номенклатурного перечня предприятия;
J2 – число составляющих оборотных активов, учитываемых в калькуляции переменных затрат производственной деятельности предприятия;
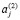 – стоимость единицы j-го переменного актива;
– стоимость единицы j-го переменного актива;
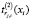 – объем затрат j-го переменного актива на производство единицы i-го вида продукции в объеме xi (в общем случае нелинейная функция в объеме производства);
– объем затрат j-го переменного актива на производство единицы i-го вида продукции в объеме xi (в общем случае нелинейная функция в объеме производства);
SK – собственный капитал предприятия, размещенный в производственном сегменте;
SK(1) – собственный капитал, используемый на финансирование затрат переменных активов;
β – планируемое значение коэффициента автономии (отношение собственного капитала к полному капиталу) – риск структуры капитала производственного сегмента предприятия;
βп – пороговое (минимальное) значение коэффициента автономии;
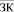 – максимально возможный объем заемного финансирования производственного сегмента предприятия;
– максимально возможный объем заемного финансирования производственного сегмента предприятия;
p1 – эффективная ставка по депозиту для предприятия в выбранном банке;
p2 – номинальная ставка по краткосрочному кредиту для предприятия в выбранном банке;
Si – спрос на i-е изделие, сложившийся на рынке для рассматриваемого периода времени.
Максимальный валовый доход VD (до налогообложения) производственного сегмента предприятия, покрывающий затраты переменных активов и по обслуживанию кредита (для рассматриваемого интервала времени), может быть рассчитан на основе следующей статичной модели производственного сегмента предприятия:
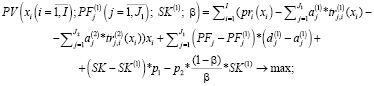 (18)
(18)
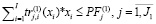 ; (19)
; (19)
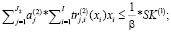 (20)
(20)
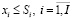 ; (21)
; (21)
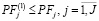 ; (22)
; (22)
SK(1) ≤ SK; (23)
β ≥ βп; (24)
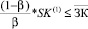 ; (25)
; (25)
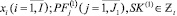 ; (26)
; (26)
β∈(0; 1). (27)
В составе переменных критерия (18) модели (18)-(27) перечислены эндогенные (управляемые), соответственно: объемы производимой продукции; постоянные активы, резервируемые для целей собственного производства; собственный капитал предприятия, планируемый для финансирования переменных затрат; коэффициент автономии.
Регулируемыми (определяемыми по результатам предыдущего производственно-коммерческого цикла) параметрами модели являются: объемы постоянных активов (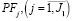 , собственного капитала (SK) производственного сегмента предприятия и пороговое значение (βп) коэффициента автономии.
, собственного капитала (SK) производственного сегмента предприятия и пороговое значение (βп) коэффициента автономии.
Нерегулируемыми (экзогенными) параметрами модели являются: рыночный спрос 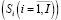 , цены
, цены 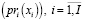 на изготавливаемую продукцию и факторы производства
на изготавливаемую продукцию и факторы производства 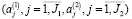 , рыночные ставки
, рыночные ставки 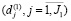 доходности по операциям сдачи/взятия активов производственного назначения в аренду, (p1, p2) по депозитам и краткосрочным кредитам и емкость
доходности по операциям сдачи/взятия активов производственного назначения в аренду, (p1, p2) по депозитам и краткосрочным кредитам и емкость 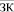 рынка заемного капитала).
рынка заемного капитала).
В группу «технологических» параметров модели включены коэффициенты 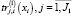 и
и 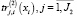 фондоемкости изделий производственной программы соответственно по элементам постоянных и переменных активов рабочего капитала производственного сегмента предприятия.
фондоемкости изделий производственной программы соответственно по элементам постоянных и переменных активов рабочего капитала производственного сегмента предприятия.
Соответствие модели (18)-(27) заявленной концепции определения оптимального размера предприятия обосновывается содержанием критерия и ограничений. В критерии (18) предложено учитывать одновременно и финансовый результат основной производственной деятельности в форме разницы стоимостей реализованной продукции и затрат на ее производство, лимитированный рыночным спросом и величинами рабочего капитала в части активов и пассивов, и альтернативные доходы производственного сегмента предприятия, связанные со сдачей в аренду излишка производственных мощностей и размещением свободных средств на банковском депозите.
Если рентабельность производимой продукции по совокупным производственным затратам, рассчитанная на основе первого слагаемого в выражении (18), выше доходности внепроизводственной деятельности (второе слагаемое в выражении (18), то приоритет будет отдан основной производственной деятельности, а для обеспечения большего объема выпуска (в пределах рыночного спроса) будут запланированы большие объемы постоянных активов 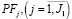 и денежных средств SK(1), направляемых в покрытие переменных затрат.
и денежных средств SK(1), направляемых в покрытие переменных затрат.
В случае невысокой рентабельности основной производственной деятельности по затратам постоянных и переменных активов и (или) низкого рыночного спроса на конечную продукцию приоритетной окажется внепроизводственная деятельность, результат которой описывается вторым слагаемым выражения (18). В этом случае резервируемая для осуществления основной производственной деятельности величина постоянных активов 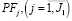 соответствует производственной мощности, обеспечивающей производство на уровне рыночного спроса на продукцию предприятия.
соответствует производственной мощности, обеспечивающей производство на уровне рыночного спроса на продукцию предприятия.
Изменяя регулируемые параметры производственного сегмента предприятия: объемы постоянных активов 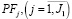 и рабочего капитала SK и пороговое значение βп коэффициента автономии (правые части ограничений (2), (6), (7), лицо, принимающее решение, имеет возможность планировать и управлять финансовым результатом производственного сегмента предприятия в случае стабильных параметров товарного и финансового рынка: спроса и цен на готовую продукцию, цен на факторы производства, процентных ставок по депозитам и кредитам, емкости рынка краткосрочных кредитов и других параметров.
и рабочего капитала SK и пороговое значение βп коэффициента автономии (правые части ограничений (2), (6), (7), лицо, принимающее решение, имеет возможность планировать и управлять финансовым результатом производственного сегмента предприятия в случае стабильных параметров товарного и финансового рынка: спроса и цен на готовую продукцию, цен на факторы производства, процентных ставок по депозитам и кредитам, емкости рынка краткосрочных кредитов и других параметров.
Таким образом, для фиксированных значений экзогенных параметров товарного и финансового рынка, перечисленных выше, оптимальный размер производственного сегмента предприятия на выбранном интервале планирования t зависит от установленных значений регулируемых параметров состава постоянных активов, объема и структуры капитала, инвестируемого в производственную сферу его рыночной деятельности. Эти значения используются в правых частях ограничений (19), (23), (24), что позволяет утверждать о наличии следующей зависимости, устанавливающей связь между оптимальным размером производственного сегмента предприятия для временного интервала t и двойственными оценками этих ограничений, соответствующих ему:
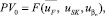 (28)
(28)
где PV0 – оптимальный размер производственного сегмента предприятия для периода t, соответствующий максимальному значению критерия (18) модели (18)-(27); 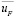 – вектор двойственных оценок ограничения на объемы постоянных активов
– вектор двойственных оценок ограничения на объемы постоянных активов 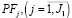 ; uSK –двойственная оценка ограничения на объем оборотного капитала производственного сегмента;
; uSK –двойственная оценка ограничения на объем оборотного капитала производственного сегмента; 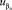 – двойственная оценка ограничения на пороговое значение риска структуры капитала.
– двойственная оценка ограничения на пороговое значение риска структуры капитала.
Комментарий 1. Для случая непрерывной задачи (в отсутствии ограничения (26)), линейных критерия и ограничений модели (18) – (27) функционал (28) может быть представлен линейной сверткой двойственных оценок и абсолютных значений правых частей ограничений (19), (23), (24).
В общем случае непрерывной нелинейной задачи (18) – (25), (27) учитывая выпуклость критерия (18) и ограничений (19) – (25) для нахождения двойственных оценок ограничений (19), (23), (25) следует составить функцию Лагранжа исследуемой модели, выписать необходимые условия её экстремума и, опираясь на соотношения теоремы Куна-Таккера, определить двойственные оценки ограничений (2) – (8) и, в том числе, (19), (23) [16, 17]. (25).
Комментарий 2. Модель (18) – (27) может быть «усилена» ограничением (14), что позволит в расчетах оптимального размера производственного сегмента предприятия учесть предельный уровень принимаемого риска потери доходности основной производственной деятельности.
Введение в модель дополнительного нелинейного ограничения типа «≤» сохранит разрешимость полной системы ограничений модели (18) – (27), (14) (легко видеть, что «тривиальное» решение 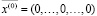 ей удовлетворяет), но повысит вычислительную сложность численного алгоритма ее решения, который рассмотрим в следующем разделе.
ей удовлетворяет), но повысит вычислительную сложность численного алгоритма ее решения, который рассмотрим в следующем разделе.
Численный алгоритм решения дискретной нелинейной задачи (18) – (25), (27), (14)
На первом этапе рассмотрим численный метод решения дискретной нелинейной задачи (18) – (25), (27) (без ограничения (14) на предельный допустимый риск производственной программы). В качестве основной идеи численной процедуры используем метод линеаризации, предложенный М.А. Горским [13].
По результатам решения задачи (18) – (25), (27) на предыдущих временных интервалах 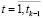 , (tk – текущий временной интервал) для каждого продукта из производственной программы предприятия определим минимальный
, (tk – текущий временной интервал) для каждого продукта из производственной программы предприятия определим минимальный 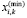 и максимальный
и максимальный 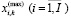 объемы его производства.
объемы его производства.
Аналогично поступим для нелинейных функционалов 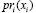 ,
, 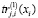 и
и 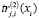 , входящих в качестве составляющих в критерий (18) и левые части ограничений (19) и (20)
, входящих в качестве составляющих в критерий (18) и левые части ограничений (19) и (20) 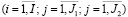 .
.
Линейные представления этих функционалов для временного интервала tk определим, используя метод «двух точек» [18, 19]:
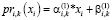 ; (29)
; (29)
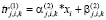 ; (30)
; (30)
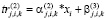 , (31)
, (31)
где
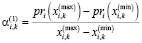 ; (32)
; (32)
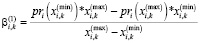 ; (33)
; (33)
(По аналогичным формулам определяются коэффициенты линеаризации 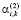 ,
, 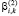 ,
, 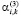 ,
, 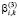 и для функционалов
и для функционалов 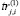 и
и 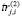 ).
).
С использованием коэффициентов линеаризации, приведенных выше, получим линейную дискретную модель следующего вида:
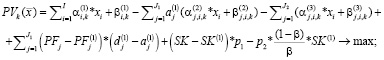 (18’)
(18’)
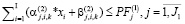 ; (19’)
; (19’)
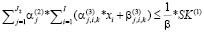 ; (20’)
; (20’)
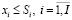 ; (21’)
; (21’)
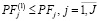 ; (22’)
; (22’)
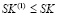 ; (23’)
; (23’)
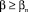 ; (24’)
; (24’)
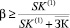 ; (25’)
; (25’)
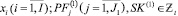 ; (26’)
; (26’)
β∈(0; 1). (27’)
Если учесть, что параметр β относится к регулируемым, то модель (19’) – (26’) эффективно решается с использованием алгоритмов дискретной оптимизации, например, методом «ветвей и границ» [16, 20, 21].
Рассмотрим алгоритм решения нелинейной задачи (19’) – (26’), (14) (с включением ограничения (14) на предельный допустимый риск производственной программы).
На временном интервале k проводим линеаризацию основной задачи (18) – (26) и решаем целочисленный аналог линейной задачи (18’) – (26’), (27’). Пусть 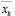 – оптимальный набор продуктов для временного интервала k.
– оптимальный набор продуктов для временного интервала k.
Если набор 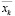 удовлетворяет ограничению (14), то оптимальное целочисленное решение для шага k найдено.
удовлетворяет ограничению (14), то оптимальное целочисленное решение для шага k найдено.
В противном случае, учитывая, что ограничение (14) задает выпуклую область допустимых решений и в совокупности с критерием (18) и другими ограничениями (19) – (26) является «стандартной» задачей линейного непрерывного программирования, то, применяя к ней симплекс – процедуру, выпишем множество базисных решений, удовлетворяющих этому ограничению:
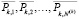 (где N(k) – число базисных решений задачи для шага k).
(где N(k) – число базисных решений задачи для шага k).
Введем в рассмотрение набор весов 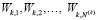 , удовлетворяющих условиям:
, удовлетворяющих условиям:
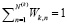 ; (34)
; (34)
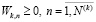 , (35)
, (35)
и вектора 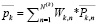 , каждый из которых удовлетворяет ограничениям (19’), (20’), (21’) и (14).
, каждый из которых удовлетворяет ограничениям (19’), (20’), (21’) и (14).
Таким образом, оптимальный набор весов (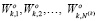 и соответствующий ему вектор
и соответствующий ему вектор 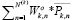 оптимального решения непрерывной задачи квадратичного выпуклого программирования (18’) – (25’), (27’), (14) могут быть получены как решение более простой задачи линейного программирования:
оптимального решения непрерывной задачи квадратичного выпуклого программирования (18’) – (25’), (27’), (14) могут быть получены как решение более простой задачи линейного программирования:
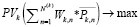 ; (18’’)
; (18’’)
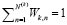 ; (34’)
; (34’)
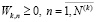 . (35’)
. (35’)
Соответствующие вектору 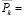
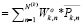 квазиоптимальное решение дискретной (с учетом ограничения (26’)) задачи может быть получено с использованием метода локальной оптимизации непрерывного решения, приведенного в работе [14].
квазиоптимальное решение дискретной (с учетом ограничения (26’)) задачи может быть получено с использованием метода локальной оптимизации непрерывного решения, приведенного в работе [14].
Заключение и выводы
В статье представлен теоретический подход, экономико-математические модели и методы оценки оптимального размера производственного сегмента промышленной корпорации в условиях изменчивых параметров рынков готовой продукции и факторов производства.
Важной особенностью подхода, моделей и методов является их реализация в рамках неоклассической теории и фирмы, предполагающая широкое использование при выборе оптимальных вариантов основной производственной и внепроизводственной деятельности производственного сегмента корпорации двойственных оценок ограничений по внешним (рыночным) и внутрифирменным параметрам, характеризующим текущее состояние внешней и внутренней её сред.
С учетом этого аспекта полученные результаты являются новыми, имеющими важное значение для современной теории и практики производственного менеджмента.
Библиографическая ссылка
Горский М.А., Халиков М.А. МОДЕЛИ И МЕТОДЫ ОЦЕНКИ ОПТИМАЛЬНОГО РАЗМЕРА ПРОИЗВОДСТВЕННОГО СЕГМЕНТА ПРЕДПРИЯТИЯ // Вестник Алтайской академии экономики и права. 2020. № 1-1. С. 23-32;URL: https://vaael.ru/ru/article/view?id=935 (дата обращения: 01.01.2026).
DOI: https://doi.org/10.17513/vaael.935

