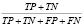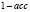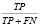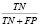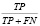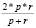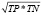Научный журнал

Вестник Алтайской академии экономики и права

Print ISSN 1818-4057

Online ISSN 2226-3977

Перечень ВАК

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Архипов В.А. 1

---

1 РЭУ им. г.В. Плеханова

Разработка моделей машинного обучения, помимо прочего, включает в себя определение оптимальной для конкретной бизнес-задачи метрики качества. Выбор корректной метрики зачастую связан с изменениями в подходе к моделированию, т.к. одни модели машинного обучения в результате оптимизации внутренней функции потерь более ориентированы на решение задачи ранжирования, другие модели – на минимизацию ошибки 1-го рода и т.д. На примере кредитного скоринга показано, что выбор оптимальной метрики качества является нетривиальной задачей с учётом особенностей различных доступных метрик. Например, максимизация интегральной метрики качества ROC-AUC далеко не всегда может приводить разработчика к желаемому в смысле бизнес-эффекта результату. Использование исключительно интегральных метрик качества может приводить к негативным результатам при применении модели. Например, в случае использования модели для принятия решения о выдаче кредита клиенту, более правильным является подход на основе балансировки показателей Precision/Recall, т.к. он позволит выбрать оптимальную модель с точки зрения стратегии кредитной организации. В данной статье рассматриваются наиболее распространенные метрики качества моделей бинарной классификации, которые позволяют принять решение о превосходстве одной модели над другой с учётом сформулированных бизнес-требований к модели. Приведенные методики расчёта метрик и их особенности позволяют выработать правила по выбору метрики качества под конкретную задачу.

Статья в формате PDF

0 KB

моделирование

кредитный скоринг

машинное обучение

метрики качества

бинарная классификация

1. Rezac M., Rezac F. How to measure the quality of credit scoring models // Finance a Uver. – 2011. – Т. 61. – № 5. – С. 486.

2. Frunza M.C. Computing a standard error for the Gini coefficient: an application to credit risk model validation // The Journal of Risk Model Validation. – 2013. – Т. 7. – № 1. – С. 61.

3. Friedman J., Hastie T., Tibshirani R. The elements of statistical learning. – New York, NY, USA: Springer series in statistics, 2001. – Т. 1. – № 10.

4. Hand D.J., Henley W.E. Statistical classification methods in consumer credit scoring: a review // Journal of the Royal Statistical Society: Series A (Statistics in Society). – 1997. – Т. 160. – № 3. – С. 523–541.

5. Siddiqi N. Credit risk scorecards: developing and implementing intelligent credit scoring. – John Wiley & Sons, 2012. – Т. 3.

6. C. Sammut and G.I. Webb, Eds., Encyclopedia of Machine Learning. New York: Springer, 2011.

Введение

Бинарная классификация – одна из наиболее распространенных проблем прикладной статистики и машинного обучения, которая решается во множестве прикладных областей – в медицине, биологии, метеорологии, анализе почтовых сообщений, кредитном скоринге, классификации текстов, изображений и т.д.

Оценка качества моделей классификации является важным аспектом во многих областях, для которых разрабатываются модели машинного обучения. Данная оценка качества отвечает на вопрос, насколько хорошо полученный классификатор разделяет интересующие нас классы на некоторой выборке. Сравнение моделей между собой на основе исключительно 4-х базовых показателей (табл.1) не представляется возможным в силу невозможности оптимизировать данные показатели под конкретную задачу, стоящую перед исследователем. В то же время, существуют метрики качества, которые позволяют сравнивать модели между собой и выбирать оптимальные, не забывая при этом о желаемом бизнес-эффекте.

В данной статье основной акцент сделан на решении задачи бинарной классификации в главном её экономическом приложении – проблеме кредитного скоринга.

Проблема кредитного скоринга является важнейшей составляющей процесса кредитования в банковской сфере. На основе результатов моделей кредитного скоринга, среди прочего, рассчитывается средний уровень вероятности дефолта (Probability of Default – PD) – одного из факторов, участвующих в расчете норматива достаточности капитала в соответствии с требованиями Базельского комитета в рамках продвинутого подхода на основе внутренних рейтингов (A-IRB). Модель напрямую влияет на предсказанные значения долгосрочной вероятности дефолта, что может приводить к существенным изменениям требований к резервному капиталу банка.

Метрики качества моделей бинарной классификации

Оценка качества построенных тем или иным методом классификаторов является важнейшей компонентой жизненного цикла моделей, особенно в сфере экономики и финансов, где эффект от ошибок 1-го и 2-го рода может генерировать существенные потери для бизнеса.

Наиболее распространенная метрика качества для моделей бинарной классификации – Area Under (ROC) Curve (AUC) позволяет получить интегральную оценку качества модели, не принимая во внимание эффекты от вариации порога отсечения (threshold). Для задачи кредитного скоринга используется иной интегральный показатель качества ранжирующей способности модели – коэффициент Джини.

Метрикой качества алгоритмов принимается коэффициент Джини [1], который непосредственно связан с CAP-кривой (Cumulative Accuracy Profile) [2].

CAP-кривая показывает, какой части дефолтных клиентов модель присваивает относительно худший скоринговый балл. Соответствующий CAP-кривой коэффициент Джини (Gini) вычисляется следующим образом [3, 4]:

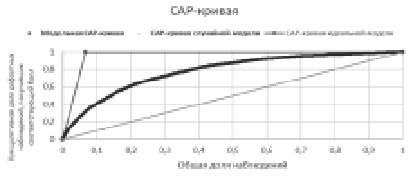
Пример CAP-кривой

Коэффициент Джини варьируется в интервале [0, 1], где 1 – идеальная модель, 0 – случайные результаты (аналогичные подбрасыванию монеты).

Тем не менее, существуют другие метрики качества моделей бинарной классификации, которые могут использоваться для идентификации сильных и слабых сторон модели применительно к конкретному бизнес-процессу, что подробно описано в работе [5].

Перед тем, как перейти к конкретным метрикам качества, стоит рассмотреть 4 базовых показателя результатов модели на некоторой выборке, для которой известны «правильные ответы» – True Positives (TP), False Positives (FP), True Negatives (TN) и False Negatives (FN). Разместив эти показатели в матрицу 2x2, мы получим матрицу неточностей для конкретной модели бинарной классификации на конкретной выборке.

Используя приведенную выше матрицу неточностей, представляется возможным и полезным получить целую серию метрик качества модели бинарной классификации, которые при это не являются взаимоисключающими, но дополняют друг друга и могут быть использованы в процессе принятия решения об оптимальной модели в каждом конкретном случае. К примеру, в задаче кредитного скоринга, ошибка 1-го рода может быть не столь критична, как ошибка 2-го рода, если глобальная стратегия банка направлена на наращивание кредитного портфеля. Напротив, если говорить о медицинской сфере, то ошибка 1-го рода является наиболее критичной, т.к. может быть более предпочтительно поставить чересчур пессимистичный диагноз, чем чересчур оптимистичный. [6]

Таблица 1

Матрица неточностей для бинарной классификации

Таблица 2

Таблица специальных метрик для конкретных порогов отсечения

Таблица 3

Метрики качества для 3-х вариантов построенных моделей

Таким образом, используя 4 приведенных выше показателя, можно прийти к следующим метрикам качества модели (в таблице приведены названия метрик качества, формулы их расчета, а также интерпретация результатов).

Проиллюстрируем важность проверки модели бинарной классификации специальными метриками помимо интегральных показателей для задачи кредитного скоринга.

Было построено 3 варианта модели бинарной классификации на данных заемщиков юридических лиц одного из крупных банков РФ, табл. 3 содержит результаты оценки качества данных моделей.

Можно видеть, что интегральный показатель ранжирующей способности модели, а также базовая точность отдают предпочтение модели 2, однако гармоническое среднее между точностью и полнотой после оптимизации порога отсечения выше для модели 3. Такое расхождение может быть вызвано более уверенным разделением модели 3 классов к «положительным» и «отрицательным», что особенно релевантно для задачи кредитного скоринга.

При этом, в конкретный момент времени финансовая организация может быть заинтересована в первую очередь в наращивании своего кредитного портфеля, допуская при этом повышенный уровень риска. В такой ситуации уместно сравнивать модели между собой на уровне конкретных порогов отсечения по метрика Precision/Recall, F-мера.

Заключение

Выбор оптимальной метрики для конкретной бизнес-задачи является ключевым шагом в разработке «правильной» модели. Корректный выбор метрики обеспечит достижение поставленных показателей эффективности процесса в целом. В статье были рассмотрены основные метрики качества моделей бинарной классификации, которые могут быть использованы при принятии решения об оптимальности разработанной модели. Было показано, что интегральные метрики качества, такие как ROC-AUC или Gini не всегда могут однозначно свидетельствовать о превосходстве одной модели над другой, т.к. оценивают исключительно ранжирующую способность, но не анализируют ошибки классификаторов при конкретных порогах отсечения.

Рассмотренные в табл. 2 метрики, в свою очередь, оперируют значениями, соответствующими именно конкретным порогам, оптимизация которых в соответствии с поставленными бизнес-задачами является главной задачей владельцев моделей для их оптимального применения.

Библиографическая ссылка