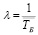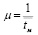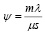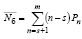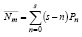Научный журнал

Вестник Алтайской академии экономики и права

Print ISSN 1818-4057

Online ISSN 2226-3977

Перечень ВАК

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Гарифуллина З.А. 1 Степанова Р.Р. 1 Хакимова И.И. 2

---

1 Филиал Уфимского государственного нефтяного технического университета

2 ЗАО «Консалтинговый Центр»

Важным признаком научной организации труда является ее направленность на решение трех взаимосвязанных задач: экономических, психофизиологических и социальных. Экономические деятельности достигаются рациональным разделением и кооперацией труда, при помощи которых обеспечивается полное использование во времени всех работников, распределение работ в соответствии с уровнем их квалификации, исключение непроизводительных простоев оборудования, минимизация длительности производственного цикла. Однако обеспечение такой организации при строительстве скважин в соответствии с месячным (годовым) планом производственно-хозяйственной деятельности предприятия возможно только при наличии определенного соотношения полностью укомплектованных буровых, вышкомонтажных бригад и других производственных звеньев. В связи с этим возникает необходимость проектирования оптимального соотношения между названными выше производственными звеньями предприятия. При проектировании структуры и размера бурового предприятия в зависимости от планируемого объема строительства скважин наиболее важным является вопрос эффективного сопряжения работы буровых и вышкомонтажных бригад, так как они наиболее тесно взаимодействуют в циклах строительства скважин, характеризуются относительно большой численностью и используют дорогостоящую технику. При этом простои этих бригад по организационным причинам связанны с наибольшими потерями материальных, трудовых и денежных средств. Авторами предлагается проводить проверку оптимального соотношения буровых и вышкомонтажных бригад плана производственно-хозяйственной деятельности на основе теории систем массового обслуживания. В работе был проведен расчет оптимального соотношения буровых и вышкомонтажных бригад с использованием системы массового обслуживания, который показал, что оптимальным с точки зрения убыточности деятельности условного предприятия необходимо следующее соотношение производственных звеньев: буровых бригад – 12; вышкомонтажных бригад – 6; бригад освоения – 5. В то время как фактически на предприятии имеются: буровых бригад – 13; вышкомонтажных бригад – 5; бригад освоения – 4.

Статья в формате PDF

0 KB

организация производства

производственный процесс

программное обеспечение

строительство скважин

система массового обслуживания

1. Особенности научной организации труда // Особенности научной организации труда. – URL: https://monographies.ru/ru/book/section?id=2094 (дата обращения 19.12.2018).

2. Андреев А.Ф. [и др.] Основы менеджмента (нефтяная и газовая промышленность): учебник / под ред. А.Ф. Андреева. – М.: ФГУП Изд-во «Нефть и газ» РГУ нефти и газа им. И.М. Губкина, 2007. – 264 с.

3. Основы экономической деятельности на буровом предприятии [Электронный ресурс]: учебное пособие для студентов очного и заочного обучения специальности 130504 «Бурение нефтяных и газовых скважин» / сост. Н.Р. Поздеева. – Уфа: УГНТУ, 2013.

4. Гарифуллина З.А. Определение критериев успеха реализации IT-проектов на предприятиях нефтяной отрасли с позиций теории функциональных систем // Нефть, газ и бизнес. – 2013. – № 6. – С. 27–34.

5. Менеджер нефтегазового предприятия [Электронный ресурс]: программа «Экономика и управление на предприятии нефтегазового комплекса»: 1 семестр: электронные учебно-методические комплексы по дисциплинам / УГНТУ, ИДПО, ЦИОТ, каф. ЭНГП. – Уфа: Изд-во УГНТУ, 2009 (дата обращения: 19.12.2018).

6. Теория массового обслуживания [Электронный ресурс] // Теория массового обслуживания. – URL: https://ru.wikipedia.org/wiki/Теория_ массового_обслуживания (дата обращения 19.12.2018).

Введение

Прикладной аспект научной организации труда направлен на поиск эффективных способов, методов формирования оптимальной организации производственного процесса. Оптимизация производственного процесса строительства скважин достигается через обеспечение полного использования во времени всех работников, распределение работ в соответствии с уровнем квалификации рабочих, максимальное исключение непроизводительных простоев оборудования, сокращение длительности производственного процесса [1].

Цель исследования

Многоэлементные процессы производства требуют правильного их сочетания в пространстве и во времени. Правильность сочетания во многом зависит от уровня организации производственного процесса и является результатом работы менеджера в рамках научной организации труда на производстве. В данной работе рассматривается совершенствование временной организации производства при строительстве скважин. Эта задача может быть решена путем моделирования, с применением теории систем массового обслуживания (СМО).

Материал и методы исследования

Теоретическое исследование, теория систем массового обслуживания, дедукция, анализ данных, итеративный метод поиска оптимального решения.

Результаты исследования и их обсуждение

В работе был проведен расчет оптимального соотношения буровых и вышкомонтажных бригад с использованием системы массового обслуживания, который показал, что оптимальным с точки зрения безубыточной деятельности, с данной производственной программой условного предприятия, является следующее соотношение производственных звеньев: буровых бригад – 12; вышкомонтажных бригад – 6. В то время как фактически на предприятии имеются: буровых бригад – 13; вышкомонтажных бригад – 5. Оптимизация количественного соотношения бригад позволит увеличить коэффициент пропорциональности до 1,00.

Производственный процесс строительства скважины обеспечивается с привлечением буровых бригад и целого ряда сервисных служб, с использованием весьма дорогостоящего оборудования, спецтехники, инструментов и электронной аппаратуры.

Строительство скважин непрерывный процесс, причем совокупность процессов должна быть последовательной, поэтому, любой сбой, несвоевременное или некачественное выполнение любого из этапов работ нарушит технологический цикл строительства скважины. В свою очередь это приведет к длительным простоям других сервисных служб, и как следствие к убыткам [2].

Обеспечить непрерывность организационно-технологического цикла строительства скважины должно четкое и своевременное выполнение каждой бригадой своей работы, как интегральной части полного цикла буровых работ.

При заключении годовых контрактов буровое предприятие исходит из своей производственной мощности, возможности эффективного сопряжения работы буровых и вспомогательных бригад, наличия техники и оборотных средств. Выполнение плана производственно-хозяйственной деятельности предприятия, в разрезе годовых либо ежемесячных показателей возможно при оптимальном соотношении между буровыми и вышкомонтажными бригадами, буровыми бригадами и бригадами освоения и т.д. В силу специфики ведения работ в строительстве скважин используется дорогостоящие машины и оборудование (до 73% в структуре стоимости основных фондов) [3], поэтому простои в строительстве по организационным причинам связанны с большими потерями материальных, трудовых и денежных средств.

Проверку оптимального соотношения между производственными подразделениями предприятия (либо сервисными службами) видится необходимым проводить до утверждения производственной программы бурового предприятия, на заключительной стадии бюджетирования [4]. Итогом проверки должны быть рассчитанные коэффициенты использования буровых и вышкомонтажных бригад, стремящиеся к 1; суммарные убытки от простоя буровых и вышкомонтажных бригад минимальные. Методика расчета приведена в [5]. Применение теории систем массового обслуживания (СМО) для проверки оптимального соотношения между производственными подразделениями предприятия при формировании производственной программы бурового предприятия видится весьма перспективным направлением в совершенствовании организации ведения буровых работ.

Теория системы массового обслуживания использует математические методы: теорию вероятности и математическую статистику. В системе массового обслуживания создается модель системы, в которой в случайные моменты времени из внешней либо внутренней среды поступают заявки, которые система должна обслужить, при наличии определенных средств производства (буровых станков) и обслуживающего персонала (вышкомонтажные бригады). Экономическим показателем эффективности системы является минимальная стоимость потерь, связанных с возможным уходом необслуженной заявки из системы (потери от простоя буровых, либо вышкомонтажных бригад) [6].

Рассмотрим методику расчета вышкомонтажных бригад с применением теории СМО при заданном количестве буровых бригад, так как эти звенья наиболее тесно взаимодействуют в цикле строительства скважин, характеризуются относительно большой численностью и используют дорогостоящую технику. Исходные данные являются условными.

Исходные данные и результаты расчета сведены в табл. 1.

Таблица 1

Расчет оптимального количества вышкомонтажных бригад

*где Pn = anP0, и 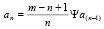для 0 < n ≤ s – 1

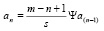для s ≤ n ≤ m

Работа системы должна быть организована так, чтобы суммарные убытки от простоя буровых и вышкомонтажных бригад были минимальны. Соответственно при поиске величины суммарных убытков задача сводится к оптимизации, на каждом шаге:

- при известных m, λ, μ определим наименьшее целое s при котором ψ < 1;

- вычисляются Nб и Nm ;

- подсчитываются убытки Уо , Уб , Ум;

- задается s+1 и осуществляется переход к следующей итерации;

- определяется sопт при котором Уо минимально,

Коэффициенты использования буровых и вышкомонтажных бригад рассчитываются по формулам:

; .

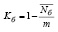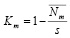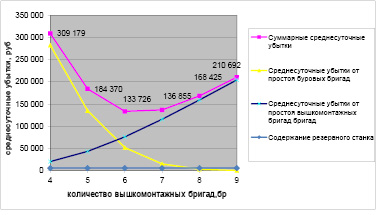
Рис. 1. Графический поиск оптимального количества вышкомонтажных бригад

На рис.1 приведен графический поиск оптимального количества вышкомонтажных бригад.

Рассчитаем коэффициенты использования буровых и вышкомонтажных бригад:

Кб = 0,99 и Км = 0,72.

Как видно из табл. 1 и рис. 1 для выполнения плана строительства скважин условному предприятию потребуется содержать 12 буровых бригад. При этом буровое предприятие будет функционировать в оптимальном режиме, если в циклах строительства скважин будет участвовать 6 вышкомонтажных бригад, при наличии одного резервного станка. Суммарные убытки при этом соотношении минимальны и составляют 133726 рублей.

Формирование дополнительной вышкомонтажной бригады и сокращение буровой бригады приведут к дополнительным расходам предприятия. Видится наиболее целесообразным иметь в наличии одну универсальную бригаду, которая могла бы совмещать разные функции, согласно производственной необходимости.

Приведенные результаты научно обоснованы, несложно решаемы и специалистам ИТ вполне по силам создать программное обеспечение, которое можно было бы встроить в расчет производственной программы бурового предприятия. Причем для проведения проверки не потребуется дополнительного ввода исходных данных, так как все эти данные рассчитаны в рамках производственной программы. Авторы считают, что внедрение в планирование буровых работ модуля проверки по расстановке в пространстве и во времени буровых и вышкомонтажных бригад на основе теории СМО позволило бы эффективно решить задачу оптимизации производственных процессов при строительстве скважин.

Заключение

Высокоорганизованное производство предполагает рациональное сочетание, чередование частных процессов во времени. Основными критериями временной организации производства служит недопущение значительных простоев вышкомонтажных бригад из-за отсутствия фронта работ, и роста незавершенного строительства из-за невостребованности соответствующего этапа работы. Авторами предлагается проводить проверку производственной программы на оптимальное соотношение буровых и вышкомонтажных бригад на основе теории систем массового обслуживания.

Библиографическая ссылка