Научный журнал

Вестник Алтайской академии экономики и права

Print ISSN 1818-4057

Online ISSN 2226-3977

Перечень ВАК

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Алексеев М.А. 1 Дудин С.А. 1 Лихутин П.Н. 1

---

1 ФГБОУ ВО Новосибирский государственный университет экономики и управления «НИНХ»

Авторами актуализирована общеэкономическая проблематика выявления таких видов мошенничества как участие в ценовом сговоре и манипулирование бухгалтерской отчетностью. Реальные совокупности, отражающие деятельность экономических субъектов, обладают свойствами турбулентности, порождаемыми информационной рефлексией хаотичной полисубъектной среды. На основе совокупностной (кейсовой) модели данных предложена методология анализа турбулентных совокупностей экономических субъектов, предположительно участвующих в ценовом сговоре и\или манипулирующих бухгалтерской отчетностью. Поставлена и последовательна решена задача на построение результирующей вероятностной модели, позволяющей построить интегральные показатели, оценивающие как достоверность ценового сговора, так и степень манипулирования бухгалтерской (финансовой) отчетностью. Логически обоснован переход от пробит моделей бинарного выбора к пробит модели множественного выбора. Проведена апробация предложенного подхода и деланы соответствующие выводы на примере таких видов деятельности как добыча сырой нефти и газа и производство пищевых продуктов. Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (РФФИ), проект № 18-010-00700.

Статья в формате PDF

435 KB

методология

совокупностная (кейсовая) модель

полисубъектная среда

теоретические выборки

турбулентные совокупности

кавитационный след

пробит регрессия

1. Алексеев М.А. Информационное пространство финансового рынка: монография. – Новосибирск: НГУЭУ, 2017. – 427 с.

2. Алексеев М.А., Дудин С.А. Показатель выявления искажения результатов деятельности компании // Вестник ИПБ (Вестник профессиональных бухгалтеров). – 2017. – № 6. – С. 36-48.

3. Алексеев М.А., Дудин С.А., Лихутин П.Н. Методология исследования турбулентных совокупностей // Вестник НГУЭУ. – 2018. – № 3. – С. 106-121.

4. Алиев А.А., Соловьева М.Г., Качалина А.Д. Интегральная оценка финансового состояния предприятия // Финансы и кредит. – 2018. – Т. 24, № 2. – С. 288-303.

5. Воищева О.С. Эконометрические модели качественных переменных в прогнозных задачах маркетинга // Вестник ВГУ. Серия: Экономика и управление. – 2006. – № 2. – С. 261-268.

6. Давнис В.В., Тинякова В.И. Прогнозные модели экспертных предпочтений: монография. – Воронеж: Изд-во Воронеж. гос. ун-та, 2005. – 248 с.

7. Лихутин П.Н., Дарьина А.А., Засеева В.В. Распознавание неявного ценового сговора на продовольственном рынке // Вестник НГУЭУ. – 2018. – № 1. – С. 103-121.

8. Лихутин П.Н., Иванова Е.С. Некоторые методические аспекты оценки вероятности ценового сговора // Сибирская финансовая школа. – 2017. – № 1 (120). – С. 66-72.

9. Страусе А., Корбин Дж. Основы качественного исследования: обоснованная теория, процедуры и техники / пер. с англ. и послесловие Т.С. Васильевой. – М: Эдиториал УРСС, 2001. – 256 с.

10. Becker H.S. Problems of Inference and Proof in Participant Observation // American Sociological Review. – 1958. – № 23(6). – С. 652-660.

11. Charmaz K. Constructing grounded theory: A practical guide through qualitative analysis. – London: Sage, 2006. – 224 с.

12. Corbin J., Strauss A. Grounded Theory Research: Procedures, Canons, and Evaluative Criteria // Qualitative Sociology. – 1990. – Vol. 13. – № 1. – С. 3-21.

13. Glaser B.G., Strauss A.L. The Discovery of Grounded Theory: Strategies for Qualitative Research / Aldine Transaction A Division of Transaction Publishers New Brunswick (U.S.A.) and London (U.K.). – 1968. – 284 c.

14. Mason J. Qualitative Researching (2nd ed.). – London: Sage, 2002. – 234 c.

15. Patton M. Purposeful sampling // Qualitative evaluation and research methods. Beverly Hills. – CA: Sage, 1990. – С. 169-186.

Введение

В России в 2012–2016 гг., несмотря на общую тенденцию снижения преступлений экономической направленности, наиболее распространенным по-прежнему остается мошенничество. Одними из основных видов мошенничества является участие в ценовом сговоре и манипулирование бухгалтерской отчетностью. Мировое профессиональное сообщество считает картельные соглашения наиболее опасными нарушениями антимонопольного законодательства. По мнению руководителя ФАС России И.Ю. Артемьева, высказанном на Правительственном часе в Государственной Думе РФ в ноябре 2016 года происходит всеобщая картелизация экономики России. За последнее время ФАС России выявила многочисленные картели в различных сферах экономики: массовые картельные сговоры на поставку имущества для МВД России, ФСБ России и ФТС России, картели на рынке лекарств, контейнерных линейных перевозок, нефтедобыча и др. Одновременно с этим практическое подтверждение получает и практика существования случаев манипулирование бухгалтерской отчетностью экономическими субъектами как в Российской Федерации, так и за рубежом. В результате опросов сотрудников 127 российских компаний в ходе всероссийского исследования, организованного Российским союзом промышленников и предпринимателей совместно с юридической фирмой VEGAS LEX, было выяснено, что 60% участников опросов сталкивались в своей деятельности с фактами корпоративных мошенничеств в своих компаниях, причем 22% из них признают, что понесли убытки свыше 100 тыс.долл. [4].

Цель исследования

Вышесказанное указывает на практическую значимость и необходимость разработки инструментария идентификации вероятности ценовых сговоров и выявления манипулирования бухгалтерской отчетностью.

По мнению авторов статьи, одним из перспективных направлений исследования проблем идентификации вероятности ценовых сговоров и оценки достоверности бухгалтерской отчетности видится построение результирующей вероятностной модели, позволяющей построить интегральные показатели, оценивающие как достоверность ценового сговора, так и степень манипулирования бухгалтерской (финансовой) отчетностью.

Материал и методы исследования

Общий методологический подход к решению поставленной задачи базируется на том факте, что реальные совокупности экономических субъектов, предположительно участвующих в ценовом сговоре и\или манипулирующих бухгалтерской отчетностью турбулентны, вследствии информационной рефлексии полисубъектной среды в условиях неопределенности, на фоне хаотичных процессов в социально-экономических системах различного уровня сложности и соподчиненности. В целях анализа турбулентных совокупностей, авторами была предложена и апробирована Совокупностная (кейсовая) модель данных, где логика исследования основывается на оценке значений заранее выделенных признаков для отнесения объекта к обучающему множеству определенного типа. [3] В рамках предложенной методологии применяются следующие подходы к анализу турбулентных совокупностей для реализации первого и второго этапов исследования [3].

Построение через противопоставление изменчивости и однородности. Цель применения данного подхода заключается в установлении логической связи между изменчивостью (однородностями) признаков множества и возникающими откликами [3,7].

Построение через противопоставление типичности и специфичности. Теоретическая выборка строится из выделения типичных и специфичных объектов наблюдения [3,2].

Построение на основе цепного отбора. Объекты в попадающие в теоретическую выборку отбираются исходя из существования формальных и/ или неформальных взаимосвязей между ними [3,7].

Построение на основе критериального отбора. В рамках подхода в теоретическую выборку отбираются объекты наблюдения, отвечающие определенным критериям [3,2].

Построение на основе доступности информации. Попадающие в теоретическую выборку объекты отбираются исходя из существования возможности доступа к внешней (общедоступной) и/или внутренней (труднодоступной) финансовой и экстрафинансовой (нефинансовой) информации [3,7,8].

Исследование совокупности экономических субъектов, предположительно участвующих в ценовом сговоре и\или манипулирующих бухгалтерской отчетностью реализуется путем последовательного прохождения следующих этапов:

Первый этап. Определение поведенческих типов экономических субъектов (таблица 1).

В целях выявления вероятности наличия ценового сговора предлагаются следующие типы: экономические субъекты, участвующие в сговоре с большой вероятностью; экономические субъекты, не участвующие в сговоре с большой долей вероятности; экономические субъекты, которые находятся «в подвешенном» состоянии, то есть они не относятся к предыдущим двум группам, и, возможно, реализуют стратегии «преследования лидера», подстраивая свое экономическое поведение под поведение экономических субъектов находящихся в ценовом сговоре. С точки зрения анализа манипулирования бухгалтерской отчетностью выделяются следующие типы: те, кто занижают результаты хозяйственной деятельности, те кто не искажают хозяйственной деятельности и те, кто завышают результаты хозяйственной деятельности.

Второй этап. Построение обучающих множеств с использованием следующих подходов: построение через противопоставление изменчивости и однородности [3,7]; построение через противопоставление типичности и специфичности [3,2]; построение на основе цепного отбора [3,7]; построение на основе критериального отбора [3,2]; построение на основе доступности информации [3,7,8].

Третий этап. Построение результирующей вероятностной модели пробит-регрессии: в случае оценки вероятности ценового сговора для компаний, участвующих с большой вероятностью в ценовом сговоре и не участвующих в ценовом сговоре; в случае анализа манипулирования бухгалтерской отчетностью для компаний, занижающих и завышающих результаты хозяйственной деятельности.

Таблица 1

Группы вероятного участия в ценовом сговоре и\или вероятного искажения финансовых результатов

Реализация первого и второго этапа достаточно полно представлена в следующих работах [2,7,8].

Реализация третьего этапа логически требует расширения пробит моделей бинарного выбора путем аналитического перехода к пробит модели множественного выбора. В рамках логики, представленной в работе Воищевой О.С. [5], начнем с рассмотрения альтернатив (используются обозначения групп из таблицы 1), заключающихся в выборе между группой «a» – (альтернатива 1) и группой «c» – (альтернатива 0). Подобный анализ, как правило, осуществляется в рамках класса моделей бинарного выбора. Введем в рассмотрение линейные функции, характеризующие экономический эффект при выборе соответствующей альтернативы.

Определим, что u1,0 – экономическая выгода для компаний группы «c» , а u1,1 – экономическая выгода для компаний группы «a».

Предположим, что экономическая выгода, для каждой из рассматриваемых альтернатив, линейно зависит от значений оцениваемого набора финансовых показателей (x1, x2, … xm), объективно отражающего результаты соответствующего выбора экономического субъекта в информационном пространстве – кавитационного следа [3]. При этом, предполагается существование непустого множества наборов финансовых показателей, включающего в себя n различных наборов Xk = (x1, x2, … xm) (где k ∈ 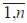), отличающихся друг от друга всеми или некоторыми своими компонентами. Обозначим через Xk вектор строку показателей, позволяющую определить экономическую выгоду при реализации k-ой альтернативы. Для каждой из рассматриваемых альтернатив экономическая выгода описывается соответствующим уравнением, что позволяет формализовать процесс выбора альтернативы экономическим субъектом через систему 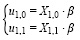(1):

(1)

где β – расширенный вектор столбец коэффициентов.

Отметим, что решение задачи определения экономической выгоды при выборе одной из альтернатив не осуществимо в явном виде. Преобладание субъективного фактора способствует тому, что экономическая выгода является не наблюдаемой (скрытой) величиной. Названная особенность выступает существенным препятствием в использовании эконометрических методов в определении коэффициентов линейных функций системы (1). Одновременно с этим, несмотря на отсутствие реальных функций, имеющих формализованное представление, в каждом конкретном случае экономический субъект имеет некоторым образом обоснованное представление о том, какая экономическая выгода последует при принятии того или иного решения об участии или не участии в ценовом сговоре или качестве составления финансовой отчетности и, как следствие, в состоянии осуществить выбор между рассматриваемыми альтернативами, таким образом, чтобы в результате получить максимальную величину чистой экономической выгоды.

Величина чистой экономической выгоды y1* может быть представлена как:

y1* = u1,1 – u1,0 = X′₁ • b + ε₁* (2)

где X′₁– различия в наборах финансовых показателей, при реализации рассматриваемых альтернатив; ε₁* – случайная ошибка, которая может быть допущена при оценке чистой экономической выгоды.

Тогда, в предположении рациональности поведения экономического субъекта, решение компании, по выбору из альтернатив, характеризующихся компаниями группы «a» и компаниями группы «c», описывается системой (3), использующей скрытую переменную y1*:

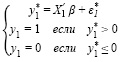(3)

где y1 – бинарная переменная, отражающая результаты выбора; y1* – чистая экономическая выгода хозяйствующего субъекта, возникающая при определенной вероятности участия в ценовом сговоре или определенном представлении результатов финансовой деятельности; X′₁ – значения объясняющих переменных (предикторов), позволяющих оценить величину чистой экономической выгоды.

Введённая выражением (2), скрытая переменная y1* в системе (3) позволяет получить отклик, выражающийся в том, что бинарная переменная y1 принимает значение равное единице для компаний группы «a» и y1 = 0, для компаний группы «с». Таким образом, переменная y1 изменяется дискретно, принимая всего два значения, что требует для установления статистической зависимости между переменной y1 и количественными данными X построения специальных регрессионных моделей [6, с.51].

Аналогичным образом, через использование скрытой переменной y2*, строится модель, представленная системой (4), описывающая решение для экономических субъектов, участвующих в ценовом сговоре или по искажению бухгалтерской (финансовой) отчетности в сторону завышения или:

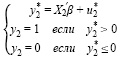(4)

где y2* – чистая экономическая выгода хозяйствующего субъекта для компаний группы «e»; X′₂ – множество объясняющих переменных (предикторов), позволяющие оценить величину чистой экономической выгоды; u2*– случайная ошибка. Так же, как и в предыдущем случае, скрытая переменная y2* позволяет получить бинарный отклик, выражающийся в том, что y2 = 1, для компаний группы «e» и y2 = 0, для компаний группы «с».

Отметим, что в общем виде множества X′₁ и X′₂ не являются тождественными.

Описанные системами (3) и (4) возможные решения экономических субъектов являются независимыми и взаимоисключающими. При независимости выбора вариантов решения совмещение систем (3) и (4) допустимо через использование бивариантной (двухвариантной) пробит модели множественного выбора.

Переход к порядковой пробит-регрессии представим путем осуществления ряда преобразований (обозначения соответствующих групп компаний из таблицы 1):

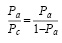(5)

где Pa – значение порядковой регрессии для компаний группы «a»;

Pc – значение порядковой регрессии для компаний группы «c».

Аналогичным образом осуществляются преобразования для компаний группы e.

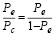(6)

где Pe – значение порядковой регрессии для компаний группы «e».

Дальнейшие преобразования полученного выражения позволяют получить следующий вид:

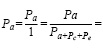
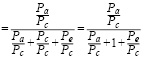(7)

Для упрощения расчетов представим сумму находящуюся в знаменателе выражения 7 через переменную А. Тогда выражение 7 для порядковой пробит-регрессии, примет следующий вид:

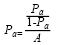(8)

Для компаний группы c выражение принимает следующий вид:

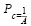(9)

Проведя аналогичные преобразования для компаний группы «e», получаем следующие выражение:

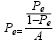(10)

Осуществив вычисления в соответствии с выражениями (8,9,10) для каждой компании, получили значения порядковой пробит-регрессии.

Полученные результаты позволяют оценить вероятность в пространстве трех возможных направлений. Полученные значения порядковой пробит-регрессии позволят осуществить распределение компаний по шести группам (таблица 1).

Результаты исследования и их обсуждение

Апробация последовательного прохождения рассмотренных этапов построения результирующей вероятностной модели пробит-регрессии осуществлена авторами на примере таких видов деятельности, как:

- добыча сырой нефти и газа в случае оценки вероятности ценового сговора для компаний, участвующих с большой вероятностью в ценовом сговоре и не участвующих в ценовом сговоре (рисунок 1);

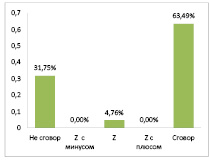
Рис. 1. Распределение компаний для оценки вероятности ценового сговора для вида деятельности добыча сырой нефти и газа в 2016 году (соответствующие обозначения в таблице 1)

Из рисунка 1 видно, что почти 64% компаний, осуществлявших деятельность по добыче сырой нефти и газа в 2016 году с высокой долей вероятности возможно участвуют в неявном ценовом сговоре. Более 30% предположительно не участвуют в ценовом сговоре. И 4,76% это экономические субъекты, которые находятся «в подвешенном» состоянии, то есть они не относятся к предыдущим двум группам. При этом доля неопределенных равна нулю.

- производство пищевых продуктов и напитков в случае анализа манипулирования бухгалтерской отчетностью для компаний, занижающих и завышающих результаты хозяйственной деятельности.

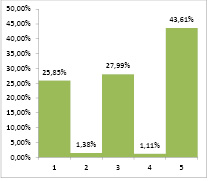
Рис. 2. Распределение компаний для анализа манипулирования бухгалтерской отчетностью, осуществляющих деятельность по производству пищевых продуктов и напитков в 2016 году (соответствующие обозначения в таблице 1)

Из рисунка 2 видно, что почти 70% компаний осуществлявших деятельность по производству пищевых продуктов и напитков в 2016 году искажают финансовые результаты хозяйственной деятельности. Из них более 43% искажают свои финансовые результаты в сторону завышения. При этом доля неопределенных совсем незначительна.

Итоги описанного подхода позволяют количественно оценить вероятность ценового сговора и определить вероятность искажения финансовых результатов деятельности экономических субъектов. Что дает нам основание считать полученные характеристики интегральным показателем, способствующим пониманию процессов, сопровождающих турбулентные совокупности в экономической среде.

Выводы или заключение

Авторами актуализирована общеэкономическая проблематика выявления таких видов мошенничества как участие в ценовом сговоре и манипулирование бухгалтерской отчетностью. Предложена методология анализа турбулентных совокупностей экономических субъектов, предположительно участвующих в ценовом сговоре и\или манипулирующих бухгалтерской отчетностью. Поставлена и последовательна решена задача: определение поведенческих типов экономических субъектов, построение обучающих множеств с использованием предложенной методологии, построение результирующей вероятностной модели пробит-регрессии для компаний, участвующих с большой вероятностью в ценовом сговоре и не участвующих в ценовом сговоре и для компаний, занижающих и завышающих результаты хозяйственной деятельности. Проведена апробация предложенного подхода и деланы соответствующие выводы на примере таких видов деятельности как добыча сырой нефти и газа и производство пищевых продуктов.

Библиографическая ссылка