Введение
Данная публикация посвящена проблематике разработки экономико-математического инструментария моделирования оптимальной по рыночному критерию динамики операционного (производственного) сегмента предприятия акционерной формы собственности с учетом ограничений по внешним и внутренним параметрам и, в том числе, риску потери финансовой устойчивости, что весьма актуально для производственной корпорации, функционирующей в условиях турбулентной рыночной среды.
В методологическом плане работа продолжает исследования по динамическим моделям микроэкономики, представленным в монографии А.М. Антиколь и М.А. Халикова [1]. В этой публикации авторы приводят оригинальные модели, в которых наряду с идеями традиционных задач производственного планирования в детерминированной и стохастической постановках, изложенных в цитируемой монографии, рассматривается новый аспект – возможность учета в моделируемой динамике «затраты-выпуск» временного лага между осуществленными инвестициями в операционный сегмент предприятия и их реальной отдачей в производственно-технологическом процессе.
Объектом исследований является производственная сфера предприятия, в которой осуществляются планирование и организация основного производственного процесса, снабжение, подготовка производства и сбыт (реализация) готовой продукции.
Цель статьи – разработка и адаптация экономико-математической модели и инструментального комплекса выбора оптимального по критерию валового маржинального дохода варианта финансирования затрат и осуществления инвестиций в операционный сегмент предприятия из собственных и заемных источников с учетом параметров товарных, материальных и финансовых рынков, риска структуры капитала производственной сферы и временного лага между инвестициями в рабочий капитал предприятия и их отдачей в форме расширения базы постоянных и переменных активов, используемых в производственно-технологическом процессе.
Материалы и методы исследования
Математический аппарат, использованный авторами при разработке методов и численных алгоритмов решения задач линейной и нелинейной оптимизации в непрерывном и целочисленном вариантах, частично заимствован из работ М. Аоки [2], Н.С. Бахвалова, Н.П. Жидкова, Г.М. Кобелькова [3], А.Ф. Грибова [17], В.А. Колемаева [8], А.А. Миролюбова, М.А. Солдатова [10], А.С. Хасанова [18], Р. Дорфмана [20], Д. Лунбергера [22]. При разработке численного алгоритма линеаризации нелинейной дискретной модели авторы использовали идеи метода, предложенного М.А. Горским [5, 13-15].
При выборе критериев и ограничений динамической модели авторы обращались к работам Д.А. Безухова [11], М.А. Бендикова, И.Э. Фролова [4], М.А. Горского [14,16].
При изложении тезисов неоклассической концепции производства, эффективности производственных факторов, оценки и управления рисками производственной сферы предприятия авторы активно цитировали работы М.А. Горского [21], Г. Б. Клейнера [6], Б. Колосса [7], М. Круи [9], О.Е. Хрусталева [19], Д. Луинбергера [10] и др. авторов [23-25],
Результаты исследования и их обсуждения
1. Динамическая модель производственной сферы предприятия.
Будем считать корректными следующие предположения:
1) зависимость в паре «затраты – выпуск» на всех интервалах планирования (t = 1,T) являются неоклассической зависимостью:
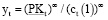
или 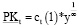 (1)
(1)
где yt – выпуск в натуральном выражение; α – степень однородности производственной функции (α > 0); ct(1) – удельные затраты (затраты на единицу выпуска) для периода t; PKt – сумма постоянных и переменных активов рабочего капитала (капитал производственной сферы предприятия) на начало временного интервалаt;
2) прибыль, полученная в операционном сегменте предприятия в периоде t, оценивается выражением:
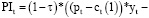
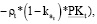 (2)
(2)
где PIt – прибыль производственного сегмента предприятия для периода t; τ – налог на прибыль хозяйствующего субъекта; pt – цена реализации продукции для периода t; pt – ставка по краткосрочному кредиту для периода t; 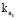 – коэффициент автономии (доля собственных средств в пассивах рабочего капитала для временного интервала t);
– коэффициент автономии (доля собственных средств в пассивах рабочего капитала для временного интервала t);
3) рабочий капитал на начало очередного планового интервала формируется из восстановленной на конец текущего периода части и собственных инвестиций из прибыли предыдущего периода, направляемых на пополнение активов операционного сегмента (инвестиции с «задержкой (лагом) на один производственно-коммерческий цикл»):
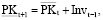 (3)
(3)
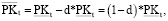 (4)
(4)
где d – коэффициент списания на амортизацию материальных активов рабочего капитала (принятый постоянным на всем горизонте при линейном способе начисления амортизации).
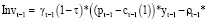
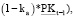 (5)
(5)
где γt–1 – доля средств из полученной на временном интервале (t-1) прибыли операционного сегмента, направляемая на собственные инвестиции в рабочий капитал в периоде (t+1).
С учетом выражения (1) балансовое соотношение (3) запишем в виде:
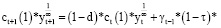
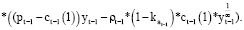 (6)
(6)
Для первого интервала будем использовать следующее соотношение:
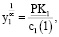 (7)
(7)
где PKt – величина активов рабочего капитала на начало первого планового периода.
Соотношение (6) является основным, связывающим динамику выпусков для производственной сферы предприятия на последовательных временных интервалах (t–1); t; (t+1) (t≥2).
Отдельно рассмотрим случай линейной производственной функции (α=1). В этом случае соотношение (6) примет вид:
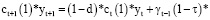
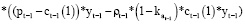
или
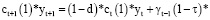
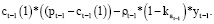 (8)
(8)
Для повышения наглядности полученного уравнения, связывающего выпуски на временных интервалах (t–1); t; (t+1), рассмотрим важный частный случай постоянных удельных затрат на всем временном горизонте: ct(1)=const, t = 1,T
В этом случае уравнение примет вид:
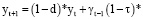
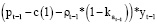 (9)
(9)
Если дополнительно предположить, что все рыночные параметры производственной сферы постоянны на всем рассматриваемом горизонте 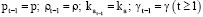 , то можно констатировать, что динамика выпусков на любых трех последовательных интервалах корректно задается однородным разностным уравнением второго порядка:
, то можно констатировать, что динамика выпусков на любых трех последовательных интервалах корректно задается однородным разностным уравнением второго порядка:
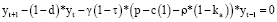 (10)
(10)
или
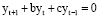 (10’)
(10’)
где b = –(1 – b); 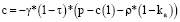 .
.
Численный алгоритм решения однородного разностного уравнения второго порядка описан в ряде работ (например, рассмотрена работа Миролюбова А.А., Солдатова М.А.) [10]. Опишем его с некоторыми изменениями, позволяющими адаптировать к рассматриваемому уравнению (10’).
Пусть λ1 и λ2 – корни характеристического уравнения:
λ2 + bλ + c = 0 (11)
Тогда общее решение исходного уравнения (10’) может быть представлено в виде:
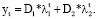 (12)
(12)
Для нахождения D1 и D2 запишем начальные точки траектории:
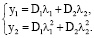 (13)
(13)
Решая эту задачу, определим значения констант D1 и D2:
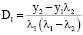 ;
; 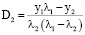 . (14)
. (14)
Из уравнения (11) следует, что
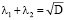 , а λ1 * λ2 = c
, а λ1 * λ2 = c
(D – дискриминант характеристического уравнения). Получим следующее выражение для решения разностного уравнения (11):
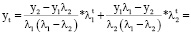
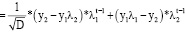 (15)
(15)
Таким образом, соотношение (15) связывает оптимальный по критерию маржинального дохода выпуск yt с оптимальными значениями выпусков на первых двух интервалах.
Если корни характеристического уравнения (11) совпадают, то решение однородного разностного уравнения (10’) может быть представлено в виде:
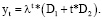 (16)
(16)
Также как и выше, для нахождения D1 и D2 используем данные о первых двух точках траектории:
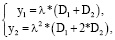 (17)
(17)
где λ = λ1 = λ2.
Решая систему (17), найдем:
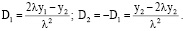 (18)
(18)
Подставим полученные значения констант D1 и D2 в соотношение (13) и получим следующую формулу для нахождения общего решения уравнения (10’) в случае совпадения корней характеристического уравнения (11):
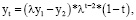 (19)
(19)
справедливую для временных интервалов t ≥ 3. Кроме того, в (19) можно дополнительно учесть, что 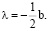
Стационарная (растущая или убывающая) динамика выпуска, задаваемого уравнением (10) или (10’) и описываемая соотношениями (15) – (18), возможна в случае, если дискриминант уравнения (11) неотрицателен, т.е.:
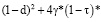
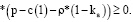 (20)
(20)
Знак левой части неравенства (20) определяется знаком выражения, состоящего в круглых скобках. Достаточным условием стационарной динамики выпуска производственного сегмента предприятия является полное покрытие из выручки удельных производственных затрат и затрат на привлекаемый заемный капитал:
p ≥ c(1) + ρ(1 – ka), (21)
что является реалистичным в условиях безубыточного производства.
2. Практические расчеты на основе динамической модели (10)-(15).
Практические расчеты динамики выпусков для производственной сферы предприятия на последовательных временных интервалах, проведены для случая α = 1 и различных комбинаций управляемых параметров ka и γ (ka=0,2; 0,4; 0,6; 0,8; γ = 0,2; 0,5; 0,8) и для следующих констант: τ=0,2; p=2; c(1)=1,2; ρ=0,15; y1=10; y2=12; d=0,04. Характер динамики конечного продукта (выпуск в натуральном выражении) для различных комбинаций отражен ниже (табл. 1-12; рис. 1-12).
Таблица 1
Динамика выпуска и рабочего капитала для α=1; ka=0,2 и γ=0,2
|
t |
PKt |
PKt |
yt |
Invt |
|
1 |
12,00 |
11,52 |
10,00 |
1,05 |
|
2 |
14,40 |
13,82 |
12,00 |
1,26 |
|
3 |
15,13 |
14,52 |
12,61 |
1,32 |
|
4 |
17,09 |
16,41 |
14,24 |
1,50 |
|
5 |
20,39 |
19,57 |
16,99 |
1,78 |
|
6 |
25,73 |
24,70 |
21,44 |
2,25 |
|
7 |
34,34 |
32,96 |
28,62 |
3,00 |
|
8 |
48,49 |
46,55 |
40,41 |
4,24 |
|
9 |
72,47 |
69,57 |
60,39 |
6,34 |
|
10 |
114,63 |
110,05 |
95,53 |
10,03 |
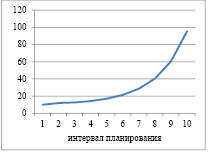
Рис. 1. Динамика выпуска и рабочего капитала для α=1; ka=0,2 и γ=0,2
Таблица 2
Динамика выпуска и рабочего капитала для α=1; ka=0,2 и γ=0,5
|
t |
PKt |
PKt |
yt |
Invt |
|
1 |
12,00 |
11,52 |
10,00 |
2,62 |
|
2 |
14,40 |
13,82 |
12,00 |
3,15 |
|
3 |
17,15 |
16,46 |
14,29 |
3,75 |
|
4 |
24,39 |
23,42 |
20,33 |
5,33 |
|
5 |
40,26 |
38,65 |
33,55 |
8,80 |
|
6 |
77,73 |
74,62 |
64,77 |
17,00 |
|
7 |
175,72 |
168,69 |
146,43 |
38,42 |
|
8 |
466,27 |
447,62 |
388,56 |
101,96 |
|
9 |
1455,0 |
1396,83 |
1212,53 |
318,17 |
|
10 |
5349,1 |
5135,15 |
4457,59 |
1169,67 |
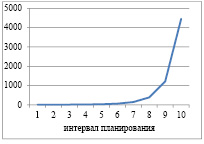
Рис. 1. Динамика выпуска и рабочего капитала для α=1; ka=0,2 и γ=0,5
Таблица 3
Динамика выпуска и рабочего капитала для α=1; ka=0,2 и γ=0,8
|
t |
PKt |
PKt |
yt |
Invt |
|
1 |
12,00 |
11,52 |
10,00 |
4,20 |
|
2 |
14,40 |
13,82 |
12,00 |
5,04 |
|
3 |
19,03 |
18,27 |
15,86 |
6,66 |
|
4 |
24,53 |
23,54 |
20,44 |
8,58 |
|
5 |
53,35 |
51,22 |
44,46 |
18,67 |
|
6 |
137,72 |
132,21 |
114,76 |
48,18 |
|
7 |
450,53 |
432,51 |
375,44 |
157,62 |
|
8 |
1863,1 |
1788,54 |
1552,55 |
651,82 |
|
9 |
9784,5 |
9393,11 |
8153,74 |
3423,27 |
|
10 |
65497,5 |
62877,6 |
54581,21 |
22915,37 |
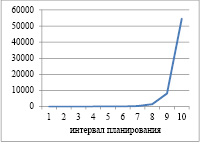
Рис. 1. Динамика выпуска и рабочего капитала для α=1; ka=0,2 и γ=0,8
Таблица 4
Динамика выпуска и рабочего капитала для α=1; ka=0,4 и γ=0,2
|
t |
PKt |
PKt |
yt |
Invt |
|
1 |
12,00 |
11,52 |
10,00 |
1,11 |
|
2 |
14,40 |
13,82 |
12,00 |
1,33 |
|
3 |
15,19 |
14,58 |
12,66 |
1,40 |
|
4 |
17,29 |
16,60 |
14,41 |
1,60 |
|
5 |
20,86 |
20,02 |
17,38 |
1,92 |
|
6 |
26,70 |
25,63 |
22,25 |
2,46 |
|
7 |
36,28 |
34,83 |
30,24 |
3,35 |
|
8 |
52,36 |
50,26 |
43,63 |
4,83 |
|
9 |
80,23 |
77,02 |
66,86 |
7,40 |
|
10 |
130,59 |
125,36 |
108,82 |
12,05 |
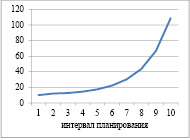
Рис. 1. Динамика выпуска и рабочего капитала для α=1; ka=0,4 и γ=0,2
Таблица 5
Динамика выпуска и рабочего капитала для α=1; ka=0,4 и γ=0,5
|
t |
PKt |
PKt |
yt |
Invt |
|
1 |
12,00 |
11,52 |
10,00 |
2,77 |
|
2 |
14,40 |
13,82 |
12,00 |
3,32 |
|
3 |
17,23 |
16,54 |
14,36 |
3,97 |
|
4 |
24,70 |
23,71 |
20,58 |
5,70 |
|
5 |
41,22 |
39,57 |
34,35 |
9,51 |
|
6 |
80,74 |
77,51 |
67,28 |
18,62 |
|
7 |
185,81 |
178,38 |
154,84 |
42,86 |
|
8 |
503,74 |
483,59 |
419,79 |
116,20 |
|
9 |
1611,9 |
1547,43 |
1343,25 |
371,81 |
|
10 |
6099,2 |
5855,23 |
5082,66 |
1406,88 |
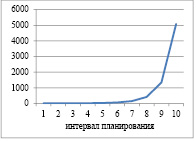
Рис. 1. Динамика выпуска и рабочего капитала для α=1; ka=0,4 и γ=0,5
Таблица 6
Динамика выпуска и рабочего капитала для α=1; ka=0,4 и γ=0,8
|
t |
PKt |
PKt |
yt |
Invt |
|
1 |
12,00 |
11,52 |
10,00 |
4,43 |
|
2 |
14,40 |
13,82 |
12,00 |
5,31 |
|
3 |
19,28 |
18,51 |
16,06 |
7,11 |
|
4 |
32,81 |
31,49 |
27,34 |
12,11 |
|
5 |
69,70 |
66,91 |
58,08 |
25,72 |
|
6 |
187,35 |
179,86 |
156,13 |
69,15 |
|
7 |
638,68 |
613,13 |
532,23 |
235,72 |
|
8 |
2778,48 |
2667,34 |
2315,40 |
1025,45 |
|
9 |
15487,11 |
14867,62 |
12905,92 |
5715,77 |
|
10 |
111040,6 |
106598,9 |
92533,82 |
40981,38 |
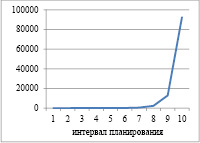
Рис. 1. Динамика выпуска и рабочего капитала для α=1; ka=0,4 и γ=0,8
Таблица 7
Динамика выпуска и рабочего капитала для α=1; ka=0,6 и γ=0,2
|
t |
PKt |
PKt |
yt |
Invt |
|
1 |
12,00 |
11,52 |
10,00 |
1,16 |
|
2 |
14,40 |
13,82 |
12,00 |
1,40 |
|
3 |
15,24 |
14,64 |
12,70 |
1,48 |
|
4 |
17,49 |
16,79 |
14,58 |
1,70 |
|
5 |
21,33 |
20,48 |
17,77 |
2,07 |
|
6 |
27,70 |
26,59 |
23,08 |
2,69 |
|
7 |
38,32 |
36,78 |
31,93 |
3,72 |
|
8 |
56,47 |
54,21 |
47,06 |
5,48 |
|
9 |
88,70 |
85,16 |
73,92 |
8,61 |
|
10 |
148,52 |
142,58 |
123,77 |
14,42 |
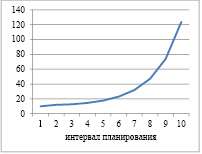
Рис. 1. Динамика выпуска и рабочего капитала для α=1; ka=0,6 и γ=0,2
Таблица 8
Динамика выпуска и рабочего капитала для α=1; ka=0,6 и γ=0,5
|
t |
PKt |
PKt |
yt |
Invt |
|
1 |
12,00 |
11,52 |
10,00 |
2,91 |
|
2 |
14,40 |
13,82 |
12,00 |
3,49 |
|
3 |
17,38 |
16,68 |
14,48 |
4,22 |
|
4 |
25,25 |
24,24 |
21,04 |
6,13 |
|
5 |
42,95 |
41,23 |
35,79 |
10,42 |
|
6 |
86,25 |
82,80 |
71,88 |
20,93 |
|
7 |
204,76 |
196,57 |
170,63 |
49,69 |
|
8 |
576,19 |
553,14 |
480,16 |
139,82 |
|
9 |
1925,94 |
1848,90 |
1604,95 |
467,36 |
|
10 |
7662,24 |
7355,75 |
6385,20 |
1859,37 |
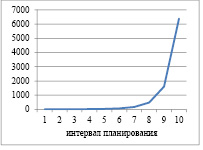
Рис. 1. Динамика выпуска и рабочего капитала для α=1; ka=0,6 и γ=0,5
Таблица 9
Динамика выпуска и рабочего капитала для α=1; ka=0,6 и γ=0,8
|
t |
PKt |
PKt |
yt |
Invt |
|
1 |
12,00 |
11,52 |
10,00 |
4,66 |
|
2 |
14,40 |
13,82 |
12,00 |
5,59 |
|
3 |
19,51 |
18,73 |
16,26 |
7,57 |
|
4 |
33,76 |
32,41 |
28,14 |
13,11 |
|
5 |
73,46 |
70,52 |
61,22 |
28,52 |
|
6 |
203,75 |
195,60 |
169,79 |
79,11 |
|
7 |
722,17 |
693,28 |
601,81 |
280,39 |
|
8 |
3292,89 |
3161,17 |
2744,08 |
1278,52 |
|
9 |
19397,81 |
18621,90 |
16164,84 |
7531,52 |
|
10 |
148243,8 |
142314,1 |
123536,5 |
57558,1 |
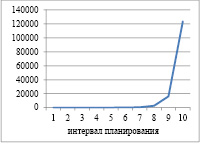
Рис. 1. Динамика выпуска и рабочего капитала для α=1; ka=0,6 и γ=0,8
Таблица 10
Динамика выпуска и рабочего капитала для α=1; ka=0,8 и γ=0,2
|
t |
PKt |
PKt |
yt |
Invt |
|
1 |
12,00 |
11,52 |
10,00 |
1,22 |
|
2 |
14,40 |
13,82 |
12,00 |
1,47 |
|
3 |
15,30 |
14,69 |
12,75 |
1,56 |
|
4 |
17,69 |
16,98 |
14,74 |
1,80 |
|
5 |
21,81 |
20,93 |
18,17 |
2,22 |
|
6 |
28,72 |
27,57 |
23,94 |
2,93 |
|
7 |
40,44 |
38,82 |
33,70 |
4,12 |
|
8 |
60,86 |
58,43 |
50,72 |
6,20 |
|
9 |
97,96 |
94,04 |
81,63 |
9,98 |
|
10 |
168,67 |
161,92 |
140,55 |
17,18 |
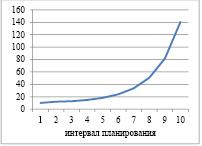
Рис. 1. Динамика выпуска и рабочего капитала для α=1; ka=0,8 и γ=0,2
Таблица 11
Динамика выпуска и рабочего капитала для α=1; ka=0,8 и γ=0,5
|
t |
PKt |
PKt |
yt |
Invt |
|
1 |
12,00 |
11,52 |
10,00 |
3,06 |
|
2 |
14,40 |
13,82 |
12,00 |
3,67 |
|
3 |
17,52 |
16,82 |
14,60 |
4,46 |
|
4 |
25,80 |
24,77 |
21,50 |
6,57 |
|
5 |
44,72 |
42,93 |
37,27 |
11,39 |
|
6 |
92,03 |
88,35 |
76,70 |
23,44 |
|
7 |
225,24 |
216,23 |
187,70 |
57,36 |
|
8 |
657,41 |
631,11 |
547,84 |
167,42 |
|
9 |
2293,57 |
2201,82 |
1911,31 |
584,10 |
|
10 |
9585,37 |
9201,95 |
7987,80 |
2441,07 |
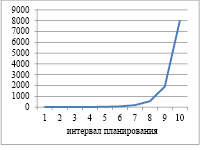
Рис. 1. Динамика выпуска и рабочего капитала для α=1; ka=0,8 и γ=0,5
Таблица 12
Динамика выпуска и рабочего капитала для α=1; ka=0,8 и γ=0,8
|
t |
PKt |
PKt |
yt |
Invt |
|
1 |
12,00 |
11,52 |
10,00 |
4,66 |
|
2 |
14,40 |
13,82 |
12,00 |
5,59 |
|
3 |
19,51 |
18,73 |
16,26 |
7,57 |
|
4 |
33,76 |
32,41 |
28,14 |
13,11 |
|
5 |
73,46 |
70,52 |
61,22 |
28,52 |
|
6 |
203,75 |
195,60 |
169,79 |
79,11 |
|
7 |
722,17 |
693,28 |
601,81 |
280,39 |
|
8 |
3292,89 |
3161,17 |
2744,08 |
1278,52 |
|
9 |
19397,81 |
18621,90 |
16164,84 |
7531,52 |
|
10 |
148243,8 |
142314,1 |
123536,5 |
57558,14 |
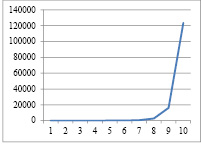
Рис. 1. Динамика выпуска и рабочего капитала для α=1; ka=0,8 и γ=0,8
Выводы
Анализируя результаты практических расчетов по динамической модели, сделаем следующие выводы:
– доля собственных инвестиций в рабочий капитал операционного сегмента предприятия – управляемый параметр, существенно влияющий на динамику выпуска, что отчетливо прослеживается по приведенным таблицам и графикам;
– чем выше доля средств, направляемая на собственные инвестиции в рабочий капитал, тем меньшее влияние на динамику выпуска оказывает коэффициент автономии (доля собственных средств в пассивах рабочего капитала);
– зависимость динамики «коэффициент автономии – темп роста выпуска» является прямо пропорциональной: с ростом коэффициента автономии растет и темп выпуска продукции, причем, весьма значительно. Данная взаимосвязь особенно прослеживается для случая γ = 0,8 (таблица 12, рис. 12).
Последний вывод особенно важен в свете рассматриваемого варианта модели операционного сегмента с учетом временного лага инвестиций в рабочий капитал предприятия; модели динамики операционного сегмента с «временным лагом» существенно отличаются от моделей динамики без его учета (модели без учета временного лага и соответствующие им расчеты динамики в паре «затраты-выпуск», подтверждающие этот вывод, приведены в работе Безухова Д.А. [11]).
Библиографическая ссылка
Халиков М.А., Стецук Ю.Ю., Струкова А.А. МОДЕЛИРОВАНИЕ ДИНАМИКИ ОПЕРАЦИОННОГО СЕГМЕНТА ПРЕДПРИЯТИЯ С УЧЕТОМ ВРЕМЕННОГО ЛАГА ИНВЕСТИЦИЙ В РАБОЧИЙ КАПИТАЛ // Вестник Алтайской академии экономики и права. 2022. № 2-2. С. 269-278;URL: https://vaael.ru/ru/article/view?id=2086 (дата обращения: 18.02.2026).
DOI: https://doi.org/10.17513/vaael.2086

