Введение
В современной экономике приоритетом рыночной деятельности производственной корпорации становится не краткосрочный критерий ее доходности и прибыльности, а долгосрочный критерий стоимости денежного потока, генерируемого в этой сфере, на величину которого существенное влияние оказывают неопределённость внешних товарных и финансовых рынков, внешние и внутренние риски и наиболее важный из них – потеря платежеспособности и банкротство. Для управления этими рисками важное значение приобретают инструменты экономико-математического моделирования и выбора оптимального варианта управления денежными потоками предприятия, реализованные в статичном и динамическом вариантах. Тематика разработки и адаптации таких моделей не является новой и представлена в работах, цитируемых ниже, а также опубликованных авторами ранее. Однако в этих работах модели денежных потоков предприятия не являются в полном смысле универсальными и не учитывают значительное число факторов его внешней и внутренней сред. В частности, в них е учитывается фактор риска структуры капитала, покрывающего затраты производственной деятельности, и стоимость заемного финансирования, влияющего на их эффективность и зависящего от этой структуры.
Цель исследования – разработка и верификация динамической модели управления денежными потоками производственной сферы предприятия с неоклассической функцией «затраты-выпуск» с учетом риска структуры рабочего капитала, влияющего на стоимость заемного финансирования затрат производственной деятельности
Методологическая основа исследования
Настоящая работа является прямым продолжением более ранних исследований проф. М.А. Халикова и его учеников, опубликованных в статьях [2,9,10]. Вид, свойства и формальные соотношения неоклассической зависимости в паре «выпуск-затраты» авторы заимствовали из работ Г.Б. Клейнера [4,5,6], Ф. Турино, П. Самуэльсона и Р. Солоу [14,15,16]. Необходимо отметить определенную связь изложенного материала с работами М.А. Бендикова [2], Б. Коласса [7], М. Круи [8] и Ю. Е. Хрусталева [11], посвященными повышению эффективности и устойчивости высокотехнологичных предприятий и холдингов, функция «выпуск-затраты» которых адекватно описывается аналитической зависимостью в неоклассической форме. Математический инструментарий методов и численных алгоритмов расчетов по динамической модели авторы разработали самостоятельно, а также частично заимствовали из работ Н.П. Бахвалова [1,12,13 (в части аппроксимации зависимости в паре «риск структуры рабочего капитала-эффективная ставка по краткосрочному банковскому кредиту)], Р. Дорфмана [12] и Д. Лиенберга [13] (в части методов решения задач математического программирования, заданных в параметрическом варианте).
Результаты исследования и их обсуждение
1. Основные понятия и соотношения динамической модели «затраты-выпуск».
В соответствии с функциями и особенностями управления рабочим (производственным) капиталом производственной сферы предприятия (отметим, что употребление термина «рабочий капитал предприятия» связано с процитированными выше работами М.А. Халикова и его учеников, в которых он связывается с переменными активами производственной сферы и покрывающими их пассивами, а также амортизируемой частью постоянного капитала) приведем следующую принципиальную схему денежных потоков его производственной сферы (рис. 1) и описание балансов их составляющих, задаваемых следующими соотношениями:
Xt = Wt + Ot + Yt ; (1)
Xt ≤ min{F(t;PKt);Spt}; (2)
Ot = τ (Xt – Wt – ρt · ЗKt-1) + (1 + ρt) · ЗKt-1 = = τ (Xt – Wt) + (1 + ρt(1–τ)) · ЗKt-1; (3)
Yt = It + Dt ; (4)
PKt+1 = Wt + It + ЗKt+1; (5)
Wt, It, Dt ≥ 0, (6)
PK0 = PKн, (7)
где t – индекс интервала планирования (t = 0,T); F(t;PKt) – производственная функция, устанавливающая зависимость в паре «валовый доход производственной деятельности – затраты производственного капитала» в условиях реализации выбранного на шаге t варианта производственной деятельности (производственной программы); Spt – рыночный спрос (в стоимостном выражении) для шага t; τ – налог на прибыль хозяйствующего субъекта; ρt – ставка по кредитам для периода t; PKн – величина производственного капитала в конце нулевого интервала планирования, равная сумме первоначального объема текущих активов и первоначальным собственным инвестициям в капитал производственной сферы.
Из (1), (3) и (4) следует:
Xt = τ Xt + (1–τ)Wt + (1 + ρt(1–τ))·ЗKt-1 + Dt + It,
откуда:
(1–τ) Xt = (1–τ)Wt + (1 + ρt(1–τ))·ЗKt-1 + Dt + It,
или
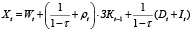 (8)
(8)
На основании (8) можно привести выражение для остаточного дохода (суммы чистых инвестиций и непроизводственного потребления):
Dt + It = (1–τ) (Xt – Wt) – (1 + ρt(1–τ))·ЗKt-1. (9)
Отметим, что соотношения (1)–(9), описывающие трансформацию производственного капитала предприятия на этапах производственно-коммерческого цикла, не включают элементы, связанные с амортизацией основного капитала. В данном случае это сделано сознательно с целью упрощения модели.
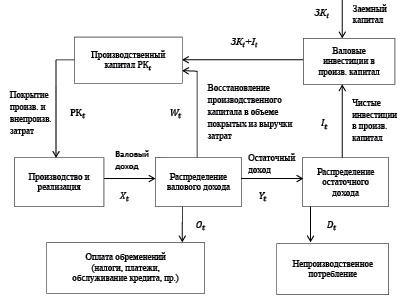
Рис.1. Схема денежных потоков производственной сферы предприятия (производственной корпорации)
Однако, здесь и далее будем считать, что амортизация используется исключительно для восстановления (реновации) основного капитала в данном или следующих плановых периодах и не используется в финансировании затрат текущей производственной деятельности (включая и оплату труда).
С учетом сделанных замечаний можно утверждать, что система уравнений (1)–(9) корректно задает Т-шаговую процедуру трансформации производственного капитала по величине и структуре и может служить основой динамической модели выбора их оптимальных по выбранному критерию величин. В качестве таких критериев рассматриваются:
- дисконтированный поток доходов собственников:
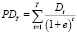 , (10)
, (10)
где е – ставка дисконтирования доходов (как правило, планируемая ставка доходности собственного капитала);
- средняя за период отдача (рентабельность) производственного капитала, авансированного в затраты:
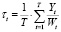 , (11)
, (11)
- средний за период индекс доходности собственных инвестиций в производственный капитал:
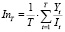 . (12)
. (12)
При этом в составе системы ограничений динамической модели предлагается дополнительно учитывать: максимально допустимый риск структуры капитала (доля заемных средств в производственном капитале) – для моделей с критериями (11), (12); минимально допустимую рентабельность и максимально допустимый риск структуры производственного капитала – для модели с критерием (10).
2. Постановка задачи моделирования экономической динамики предприятия с неоклассической производственной функцией.
Рассмотрим постановку задачи моделирования экономической динамики предприятия для важного частного случая, когда зависимость между выпуском и затратами задается неоклассической производственной функцией степени однородности α (α > 0). Напомним, степень однородности (масштаб производства) – характеристика роста объема выпуска при росте совокупных затрат рабочего капитала на один процент. Если в границах экономической области предприятия производственная функция является однородной степени α, то зависимость в паре «выпуск-затраты» корректно описывается соотношением:
c(vt) = c(1) · vt1/α, (13)
где vt – величина выпуска (в натуральном или стоимостном выражениях) для периода планирования t; c(vt) – совокупные затраты на объем выпуска vt; c(1) – удельные затраты.
Из (13) следует:
vt = (c(vt) / c(1))α. (13’)
Так как производственный капитал полностью покрывает затраты, то представим (13’) в виде:
vt = (PKt)α / z, (14)
где PKt – производственный капитал, сформированный в начале периода t и направляемый на покрытие затрат операционной деятельности этого периода; z = (c(1))α.
Если βt – доля заемного капитала, а CsPKt – величина собственных средств в производственном капитале для периода t, то
PKt = CsPKt / (1 – βt). (15)
CsPKt – часть собственного капитала Cst предприятия в начале периода t, который образуется из чистой прибыли и покрытых из выручки затрат операционной деятельности периода (t – 1).
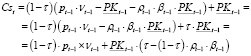 (16)
(16)
где τ – налог на прибыль; pt–1 – стоимость продукции для периода (t – 1); ρt–1 – стоимость заёмных средств (в объёме βt–1 · PKt–1), включаемых в производственный капитал для периода (t – 1).
Производственный капитал PKt, формируемый для периода t, образуется путем выделения собственниками регулируемой доли γt из собственных средств Cst на начало периода t и краткосрочного кредита, доля которого соответствует рычагу капитала βt:
PKt = γt · Cst / (1 – βt) (17)
или с учетом (16):
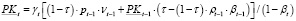 . (18)
. (18)
На основании (14) делаем вывод, что:
PKt = (vt-1 · z)1/α или
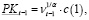 (14’’)
(14’’)
С учетом (14’’) представим (18) в виде:
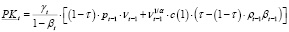 . (19)
. (19)
Используя соотношения (14) и (19), получим следующее рекуррентное уравнение, связывающее выпуски vt и vt-1 на последовательных интервалах планирования:
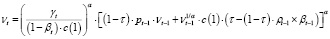 . (20)
. (20)
Возвращаясь к формуле (16) расчета величины Cst собственного капитала по завершении периода (t – 1), определим ту его часть, которая направляется в фонд потребления и в дальнейшем выплачивается акционерам в форме дивидендов.
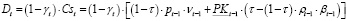 , (21)
, (21)
где Dt – абсолютный прирост фонда потребления в конце периода t.
В динамической модели предприятия, задаваемой соотношениями (19)–(21), экзогенными (неуправляемыми) параметрами являются: ставка τ налогообложения прибыли, вектора р и ρ цен соответственно товарного и финансового рынков (по интервалам планирования).
Детерминантами модели являются показатели используемой технологии: α – степень однородности (суммарная эластичность производственной функции), c(1) – удельные затраты.
Эндогенными (управляемыми) параметрами являются: vt – объем выпуска в первом плановом периоде, вектора 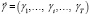 и
и 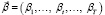 относительных долей соответственно пополнения производственного капитала предприятия из собственных средств и финансирования операционной деятельности из заёмных источников.
относительных долей соответственно пополнения производственного капитала предприятия из собственных средств и финансирования операционной деятельности из заёмных источников.
Таким образом, уравнения (19)–(21) задают возможные траектории изменения объемов средств в производственном капитале и в фонде потребления предприятия в зависимости от проводимой собственниками и менеджментом политики в сфере финансирования производственной деятельности. Последняя включает выбор структуры производственного капитала (управление долей βt заёмных средств) и его объёма (управление долей γt собственных средств, вкладываемых в производство).
3. Эмпирические расчеты по динамической модели.
Практическое значение динамической модели (19)–(21), заключается в возможности решения следующих задач производственного и финансового планирования:
- выбор оптимального по рыночному критерию (максимум финансового результата операционной деятельности) объёма производства, величины и структуры производственного капитала для следующего интервала планирования, исходя из его величины и структуры в текущем периоде, изменений экзогенных и эндогенных параметров функционирования предприятия;
- определение оптимальных пропорций в собственные инвестиции в рабочий капитал и непроизводственное потребление.
Для исследования экономической динамики предприятия с нелинейной неоклассической производственной функцией, задаваемой уравнениями (19)–(21), будем предполагать заданными: ставку τ налогообложения прибыли, цены p – товарного и ρ – финансового рынков, а также технологические константы: c(1) (удельные затраты) и v1 (выпуск на первом интервале планирования – в натуральных единицах).
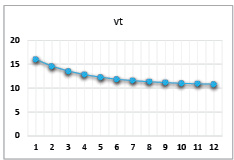
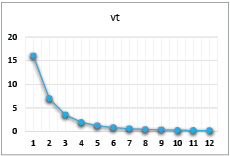
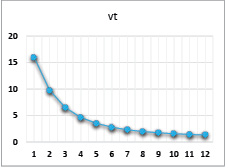
В первой части эмпирических исследований экономической динамики предприятия с неоклассической производственной функцией представим результаты расчетов по динамической модели для случая функции степени однородности α = 0,8 по нашим исследованиям достаточно приближенный к реальной практике реального сектора экономики масштаб производства производственных корпораций) и для различных комбинаций управляемых параметров γt и βt. Эти расчеты проведены для следующих рыночных и технологических констант: τ = 0,20; p = 2; c(1) = 1,2; ρ= 0,15; v1 = 16; CS1 = 0. Характер динамики выпуска для различных комбинаций параметров γt, βt отражен в табл. 1-4, а результаты расчетов приведены на рисунках 2-4.
Таблица 1
(расчеты для параметров α = 0,8, β = 0,4, γ = 0,4)
|
t |
PKt |
vt |
Dt |
|
1 |
0 |
16 |
0 |
|
2 |
5,8027 |
7,9414 |
15,3600 |
|
3 |
3,7782 |
4,5733 |
8,1262 |
|
4 |
2,5241 |
2,9578 |
4,7176 |
|
5 |
1,7896 |
2,0955 |
3,0581 |
|
6 |
1,3477 |
1,5950 |
2,1666 |
|
7 |
1,0704 |
1,2848 |
1,6479 |
|
8 |
0,8890 |
1,0823 |
1,3261 |
|
9 |
0,7659 |
0,9447 |
1,1160 |
|
10 |
0,6798 |
0,8480 |
0,9732 |
|
11 |
0,6181 |
0,7784 |
0,8730 |
|
12 |
0,5729 |
0,7272 |
0,8008 |
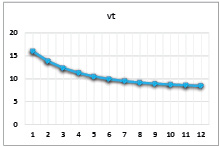
Рис. 2. Динамика выпуска при значениях параметров α = 0,8, β = 0,4, γ = 0,4
Таблица 2
(расчеты для параметров α = 0,8, β = 0,8, γ = 0,4)
|
t |
PKt |
vt |
Dt |
|
1 |
0 |
16 |
0 |
|
2 |
-31,7440 |
17,2322 |
15,3600 |
|
3 |
-35,8610 |
18,2269 |
15,7323 |
|
4 |
-39,2911 |
19,0165 |
16,5821 |
|
5 |
-42,0786 |
19,6351 |
17,2525 |
|
6 |
-44,3013 |
20,1150 |
17,7751 |
|
7 |
-46,0489 |
20,4847 |
18,1791 |
|
8 |
-47,4081 |
20,7677 |
18,4894 |
|
9 |
-48,4568 |
20,9836 |
18,7264 |
|
10 |
-49,2610 |
21,1477 |
18,9069 |
|
11 |
-49,8750 |
21,2721 |
19,0439 |
|
12 |
-50,3420 |
21,3663 |
19,1476 |
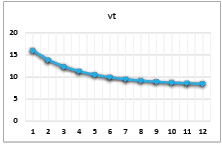
Рис. 3. Динамика выпуска при значениях параметров α = 0,8, β = 0,8, γ = 0,4
Таблица 3
(расчеты для параметров α = 0,8, β = 0,4, γ = 0,8)
|
t |
PKt |
vt |
Dt |
|
1 |
0 |
16 |
0 |
|
2 |
11,6053 |
13,8268 |
5,1200 |
|
3 |
10,7267 |
12,3264 |
4,7596 |
|
4 |
10,0364 |
11,2605 |
4,2541 |
|
5 |
9,5006 |
10,4863 |
3,8931 |
|
6 |
9,0861 |
9,9139 |
3,6298 |
|
7 |
8,7651 |
9,4849 |
3,4347 |
|
8 |
8,5162 |
9,1598 |
3,2882 |
|
9 |
8,3225 |
8,9114 |
3,1769 |
|
10 |
8,1716 |
8,7202 |
3,0919 |
|
11 |
8,0536 |
8,5724 |
3,0263 |
|
12 |
7,9614 |
8,4576 |
2,9756 |
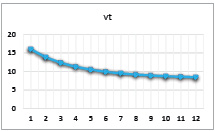
Рис. 4. Динамика выпуска при значениях параметров α = 0,8, β = 0,4, γ = 0,8
Таблица 4
Характер экономической динамики предприятия с неоклассической производственной функцией
|
α |
γt |
βt |
Динамика «выпуск-затраты» |
|
0,8 |
0,4 |
0,4 |
Экспоненциальное падение |
|
0,8 |
0,8 |
0,4 |
Квазилинейный рост |
|
0,83 |
0,8 |
0,3 |
Умеренное экспоненциальное падение |
Модель адекватна и корректно описывает характер поведения динамики выпуска в производственной сфере предприятия в соответствии с изменениями параметров γt, βt (растут инвестиции в рабочий капитал – растет выпуск конечного продукта; растет доля заемных средств и увеличивается риск рабочего капитала – растет выпуск не только по причине роста объема финансирования затрат, но и по причине положительного влияния заемного финансирования на эффективность затрат собственного капитала).
В целом, приведенные теоретические обоснования модели «выпуск-затраты» и практические расчеты убедительно демонстрируют актуальность постановки задачи оптимизации структуры производственного капитала предприятия на основе корректного определения управляемых параметров, в качестве которых предложено использовать темп накопления в производственном капитале собственных средств и коэффициент долга.
Однако в модели не учтена зависимость ставки заемного финансирования от плеча финансового рычага, в связи с чем предлагается установить эту зависимость с использованием интерполяционного многочлена Лагранжа.
Рассмотрим математический инструментарий методов конструирования функциональной зависимости в паре «уровень риска структуры капитала – процентная ставка по кредиту». В качестве такого предложено использовать интерполяционный многочлен Лагранжа [3] степени n-1, построенный на основе известных значений пары «структура капитала-стоимость заемного финансирования»: {(lk, rk), k = 1,n}
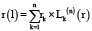 , (22)
, (22)
где n – степень интерполяционного многочлена, k – индекс узловой точки; Lk(n) – лагранжевый коэффициент:
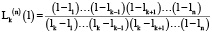 . (23)
. (23)
Представим полином (23) в виде:
y = Ln(x) = a0 + a1x + a2x2 + … + anxn (24)
где ak (k = 0,n) – коэффициенты, полученные на основе пар (xk; yk) (k = 0,n).
Для целей минимизации возможной ошибки аппроксимации функции y = f(x) полиномом (24) степени n рекомендуется использовать контрольную процедуру, включающую следующие этапы:
- построить полиномы (24) для различных значений n;
- определить значение полинома оцениваемой степени n в отдельно выбранных (не используемых в основном алгоритме) контрольных узлах и сопоставить фактические значения зависимой переменной y с истинными значениями yk;
- рассчитать ошибку аппроксимации для каждого построенного полинома и выбрать полином, обеспечивающий наименьшую погрешность.
Однако приведенная схема выбора интерполяционного полинома не является идеальной, поскольку ошибка аппроксимации непосредственно зависит от выбора узловых точек xk.
Тем не менее, предполагая определенной аналитическую форму интерполяционного полинома, перейдем к описанию процедуры формирования барьерного значения коэффициента автономии на основе задаваемого значения цены заемного финансирования.
В качестве цены заемного финансирования y в силу отсутствия иной информации нами принято решение использовать средневзвешенную ставку по рублевым кредитам, предоставляемых Центральным банком РФ за период 2014-2019 гг. нефинансовым организациям на срок до одного года (в этом качестве выбрано ОАО «Сургутнефтегаз») (таблица 5). Значение коэффициента автономии и для ОАО «СУРГУТНЕФТЕГАЗ» приведено в таблице 6.
За исследуемый временной интервал принимается период с 2014 по 2019 гг., все показатели являются среднегодовыми. На основе данных таблиц 5 и 6 построим полином третьей степени с рассчитанными лагранжевыми коэффициентами ak:
r(l) = 117968,541 – 385989,0819 × x + + 420817,9832 × x2 + 152841,08375 × x3 (26)
Произведем исследование экономической динамики предприятия с нелинейной неоклассической производственной функцией при заданном значении отдачи от масштаба производства α = 0,8 и со следующими фиксированными показателями: ставкой τ = 0,20 налогообложения прибыли, ценами p = 2 – товарного и ρ = 0,15 – финансового рынков, а также с технологическими константами: c(1) = 1,2 (удельные затраты) и v1 = 16 (выпуск на первом интервале планирования – в натуральных единицах), CS1 = 0.
Пусть ставка кредита зависит от доли заёмных средств в производственном капитале в соответствии с формулой (26) (в которой, х = β). Проведем расчеты экономической динамики предприятия (в данном случае, аналога ОАО «СУРГУТНЕФТЕГАЗ») с переменной ставкой заемного финансирования, задаваемой формулой (26).
Таблица 5
Средневзвешенная ставка по рублевым кредитам нефинансовым организациям сроком до одного года
|
Год |
2014 |
2015 |
2016 |
2017 |
2018 |
2019 |
|
r (ставка, %) |
12,32 |
16,46 |
13,7 |
11,17 |
9,28 |
9,52 |
Таблица 6
Значение коэффициента автономии для ОАО «СУРГУТНЕФТЕГАЗ»
|
Год |
2014 |
2015 |
2016 |
2017 |
2018 |
2019 |
|
коэффициент автономии |
0,919 |
0,866 |
0,932 |
0,975 |
0,985 |
0,940 |
Таблица 7
(расчеты для параметров α = 0,8, β = 0,2, γ = 0,4)
|
t |
PKt |
vt |
Dt |
|
1 |
0 |
16 |
0 |
|
2 |
16,161 |
6,494 |
15,360 |
|
3 |
6,284 |
3,172 |
7,932 |
|
4 |
2,982 |
1,793 |
3,705 |
|
5 |
1,652 |
1,138 |
2,034 |
|
6 |
1,034 |
0,793 |
1,266 |
|
7 |
0,713 |
0,594 |
0,870 |
|
8 |
0,530 |
0,472 |
0,645 |
|
9 |
0,419 |
0,393 |
0,509 |
|
10 |
0,347 |
0,339 |
0,421 |
|
11 |
0,299 |
0,302 |
0,362 |
|
12 |
0,265 |
0,275 |
0,321 |
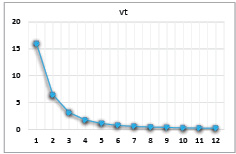
Рис. 5. Динамика выпуска при значениях параметров α = 0,8, β = 0,2, γ = 0,4
Таблица 8
(расчеты для параметров α = 0,8, β = 0,6, γ = 0,4)
|
t |
PKt |
vt |
Dt |
|
1 |
0 |
16 |
0 |
|
2 |
29,520 |
10,537 |
15,360 |
|
3 |
19,184 |
7,617 |
11,923 |
|
4 |
13,738 |
5,916 |
8,488 |
|
5 |
10,596 |
4,857 |
6,521 |
|
6 |
8,655 |
4,163 |
5,312 |
|
7 |
7,389 |
3,690 |
4,527 |
|
8 |
6,530 |
3,357 |
3,995 |
|
9 |
5,928 |
3,118 |
3,623 |
|
10 |
5,495 |
2,942 |
3,356 |
|
11 |
5,179 |
2,811 |
3,161 |
|
12 |
4,943 |
2,712 |
3,015 |
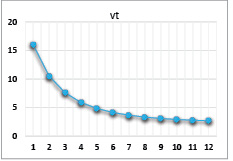
Рис. 6. Динамика выпуска при значениях параметров α = 0,8, β = 0,6, γ = 0,4
Таблица 9
(расчеты для параметров α = 0,8, β = 0,8, γ = 0,4)
|
t |
PKt |
vt |
Dt |
|
1 |
0 |
16 |
0 |
|
2 |
54,469 |
17,232 |
15,360 |
|
3 |
58,729 |
18,227 |
17,934 |
|
4 |
62,173 |
19,016 |
18,998 |
|
5 |
64,909 |
19,635 |
19,843 |
|
6 |
67,054 |
20,115 |
20,507 |
|
7 |
68,719 |
20,485 |
21,023 |
|
8 |
70,002 |
20,768 |
21,420 |
|
9 |
70,985 |
20,984 |
21,725 |
|
10 |
71,735 |
21,148 |
21,957 |
|
11 |
72,305 |
21,272 |
22,134 |
|
12 |
72,737 |
21,366 |
22,268 |
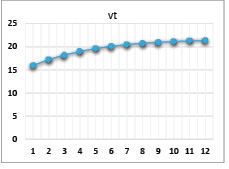
Рис. 7. Динамика выпуска при значениях параметров α = 0,8, β = 0,8, γ = 0,4
Таблица 10
(расчеты для параметров α = 0,8, β = 0,2, γ = 0,6)
|
t |
PKt |
vt |
Dt |
|
1 |
0 |
16 |
0 |
|
2 |
24,241 |
8,983 |
10,240 |
|
3 |
13,229 |
5,678 |
7,446 |
|
4 |
8,194 |
3,942 |
4,560 |
|
5 |
5,606 |
2,949 |
3,097 |
|
6 |
4,147 |
2,340 |
2,280 |
|
7 |
3,264 |
1,947 |
1,788 |
|
8 |
2,698 |
1,681 |
1,474 |
|
9 |
2,319 |
1,496 |
1,265 |
|
10 |
2,056 |
1,363 |
1,120 |
|
11 |
1,868 |
1,266 |
1,016 |
|
12 |
1,730 |
1,193 |
0,941 |
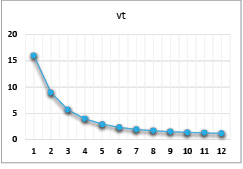
Рис. 8. Динамика выпуска при значениях параметров α = 0,8, β = 0,2, γ = 0,6
Таблица 11
(расчеты для параметров α = 0,8, β = 0,6, γ = 0,6)
|
t |
PKt |
vt |
Dt |
|
1 |
0 |
16 |
0 |
|
2 |
44,280 |
14,574 |
10,240 |
|
3 |
40,209 |
13,556 |
11,135 |
|
4 |
37,313 |
12,815 |
10,317 |
|
5 |
35,211 |
12,268 |
9,725 |
|
6 |
33,661 |
11,859 |
9,289 |
|
7 |
32,504 |
11,550 |
8,964 |
|
8 |
31,633 |
11,316 |
8,719 |
|
9 |
30,972 |
11,137 |
8,534 |
|
10 |
30,468 |
11,000 |
8,392 |
|
11 |
30,081 |
10,895 |
8,284 |
|
12 |
29,784 |
10,814 |
8,201 |
Таблица 12
(расчеты для параметров α = 0,8, β = 0,8, γ = 0,6)
|
t |
PKt |
vt |
Dt |
|
1 |
0 |
16 |
0 |
|
2 |
81,703 |
23,835 |
10,240 |
|
3 |
122,476 |
32,193 |
16,645 |
|
4 |
166,276 |
40,322 |
22,689 |
|
5 |
209,114 |
47,681 |
28,637 |
|
6 |
248,066 |
53,987 |
34,076 |
|
7 |
281,560 |
59,171 |
38,775 |
|
8 |
309,163 |
63,300 |
42,662 |
|
9 |
331,197 |
66,514 |
45,775 |
|
10 |
348,372 |
68,973 |
48,207 |
|
11 |
361,524 |
70,830 |
50,073 |
|
12 |
371,465 |
72,219 |
51,486 |
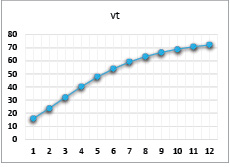
Рис. 10. Динамика выпуска при значениях параметров α = 0,8, β = 0,8, γ = 0,6
Таблица 13
(расчеты для параметров α = 0,83, β = 0,2, γ = 0,4)
|
t |
PKt |
vt |
Dt |
|
1 |
0 |
16 |
0 |
|
2 |
15,765 |
6,986 |
15,360 |
|
3 |
6,681 |
3,523 |
8,362 |
|
4 |
3,297 |
2,001 |
4,084 |
|
5 |
1,843 |
1,253 |
2,267 |
|
6 |
1,140 |
0,851 |
1,396 |
|
7 |
0,767 |
0,618 |
0,936 |
|
8 |
0,553 |
0,474 |
0,673 |
|
9 |
0,422 |
0,380 |
0,513 |
|
10 |
0,337 |
0,317 |
0,409 |
|
11 |
0,280 |
0,273 |
0,340 |
|
12 |
0,240 |
0,241 |
0,291 |
Таблица 14
(расчеты для параметров α = 0,83, β = 0,6, γ = 0,4)
|
t |
PKt |
vt |
Dt |
|
1 |
0 |
16 |
0 |
|
2 |
29,058 |
11,648 |
15,360 |
|
3 |
20,997 |
9,001 |
12,962 |
|
4 |
16,130 |
7,298 |
9,927 |
|
5 |
13,019 |
6,152 |
7,994 |
|
6 |
10,936 |
5,352 |
6,703 |
|
7 |
9,488 |
4,778 |
5,808 |
|
8 |
8,451 |
4,355 |
5,168 |
|
9 |
7,690 |
4,038 |
4,699 |
|
10 |
7,120 |
3,797 |
4,348 |
|
11 |
6,686 |
3,610 |
4,081 |
|
12 |
6,351 |
3,465 |
3,875 |
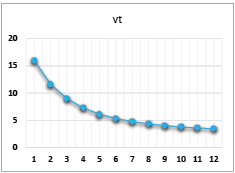
Рис. 12. Динамика выпуска при значениях параметров α = 0,83, β = 0,6, γ = 0,4
Таблица 15
(расчеты для параметров α = 0,83, β = 0,8, γ = 0,4)
|
t |
PKt |
vt |
Dt |
|
1 |
0 |
16 |
0 |
|
2 |
54,084 |
19,576 |
15,360 |
|
3 |
66,320 |
22,994 |
20,174 |
|
4 |
78,044 |
26,137 |
23,767 |
|
5 |
88,847 |
28,940 |
27,084 |
|
6 |
98,497 |
31,378 |
30,051 |
|
7 |
106,902 |
33,457 |
32,638 |
|
8 |
114,077 |
35,203 |
34,849 |
|
9 |
120,106 |
36,649 |
36,708 |
|
10 |
125,106 |
37,837 |
38,250 |
|
11 |
129,211 |
38,803 |
39,518 |
|
12 |
132,555 |
39,585 |
40,550 |
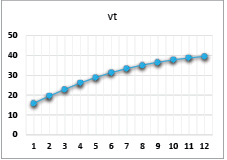
Рис. 13. Динамика выпуска при значениях параметров α = 0,83, β = 0,8, γ = 0,4
Таблица 16
(расчеты для параметров α = 0,83, β = 0,2, γ = 0,6)
|
t |
PKt |
vt |
Dt |
|
1 |
0 |
16 |
0 |
|
2 |
23,648 |
9,781 |
10,240 |
|
3 |
14,195 |
6,514 |
7,915 |
|
4 |
9,323 |
4,656 |
5,163 |
|
5 |
6,592 |
3,527 |
3,632 |
|
6 |
4,952 |
2,804 |
2,719 |
|
7 |
3,910 |
2,319 |
2,141 |
|
8 |
3,217 |
1,982 |
1,758 |
|
9 |
2,738 |
1,741 |
1,494 |
|
10 |
2,396 |
1,564 |
1,306 |
|
11 |
2,146 |
1,431 |
1,168 |
|
12 |
1,959 |
1,329 |
1,066 |
Таблица 17
(расчеты для параметров α = 0,83, β = 0,6, γ = 0,6)
|
t |
PKt |
vt |
Dt |
|
1 |
0 |
16 |
0 |
|
2 |
43,588 |
16,309 |
10,240 |
|
3 |
44,449 |
16,564 |
12,217 |
|
4 |
45,161 |
16,773 |
12,416 |
|
5 |
45,747 |
16,946 |
12,579 |
|
6 |
46,229 |
17,087 |
12,713 |
|
7 |
46,623 |
17,202 |
12,823 |
|
8 |
46,946 |
17,296 |
12,913 |
|
9 |
47,209 |
17,373 |
12,986 |
|
10 |
47,424 |
17,436 |
13,046 |
|
11 |
47,599 |
17,486 |
13,095 |
|
12 |
47,741 |
17,528 |
13,135 |
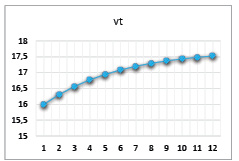
Рис. 15. Динамика выпуска при значениях параметров α = 0,83, β = 0,6, γ = 0,6
Таблица 18
(расчеты для параметров α = 0,83, β = 0,8, γ = 0,6)
|
t |
PKt |
vt |
Dt |
|
1 |
0 |
16 |
0 |
|
2 |
81,126 |
27,408 |
10,240 |
|
3 |
139,833 |
42,076 |
18,922 |
|
4 |
215,832 |
59,086 |
29,309 |
|
5 |
304,487 |
77,216 |
41,489 |
|
6 |
399,451 |
95,262 |
54,602 |
|
7 |
494,371 |
112,264 |
67,768 |
|
8 |
584,105 |
127,597 |
80,265 |
|
9 |
665,242 |
140,950 |
91,606 |
|
10 |
736,062 |
152,266 |
101,533 |
|
11 |
796,180 |
161,651 |
109,981 |
|
12 |
846,109 |
169,305 |
117,011 |
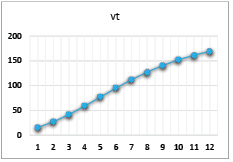
Рис. 16. Динамика выпуска при значениях параметров α = 0,83, β = 0,8, γ = 0,6
Таблица 19
(расчеты для параметров α = 0,86, β = 0,2, γ = 0,4)
|
t |
PKt |
vt |
Dt |
|
1 |
0 |
16 |
0 |
|
2 |
15,439 |
7,512 |
15,360 |
|
3 |
7,105 |
3,930 |
8,833 |
|
4 |
3,660 |
2,255 |
4,519 |
|
5 |
2,074 |
1,400 |
2,549 |
|
6 |
1,276 |
0,931 |
1,562 |
|
7 |
0,841 |
0,655 |
1,027 |
|
8 |
0,588 |
0,485 |
0,717 |
|
9 |
0,433 |
0,375 |
0,527 |
|
10 |
0,333 |
0,300 |
0,405 |
|
11 |
0,266 |
0,248 |
0,323 |
|
12 |
0,219 |
0,211 |
0,266 |
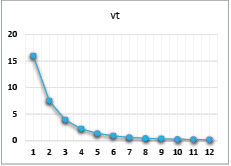
Рис. 17. Динамика выпуска при значениях параметров α = 0,86, β = 0,2, γ = 0,4
Таблица 20
(расчеты для параметров α = 0,86, β = 0,2, γ = 0,4)
|
t |
PKt |
vt |
Dt |
|
1 |
0 |
16 |
0 |
|
2 |
28,678 |
12,859 |
15,360 |
|
3 |
22,961 |
10,686 |
14,101 |
|
4 |
19,022 |
9,134 |
11,665 |
|
5 |
16,219 |
7,997 |
9,934 |
|
6 |
14,169 |
7,144 |
8,670 |
|
7 |
12,635 |
6,492 |
7,726 |
|
8 |
11,465 |
5,985 |
7,006 |
|
9 |
10,557 |
5,586 |
6,448 |
|
10 |
9,844 |
5,269 |
6,010 |
|
11 |
9,276 |
5,014 |
5,661 |
|
12 |
8,820 |
4,806 |
5,381 |
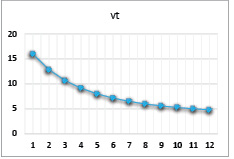
Рис. 18. Динамика выпуска при значениях параметров α = 0,86, β = 0,6, γ = 0,4
Таблица 21
(расчеты для параметров α = 0,86, β = 0,8, γ = 0,4)
|
t |
PKt |
vt |
Dt |
|
1 |
0 |
16 |
0 |
|
2 |
53,767 |
22,179 |
15,360 |
|
3 |
74,725 |
29,148 |
22,665 |
|
4 |
98,428 |
36,620 |
29,890 |
|
5 |
123,907 |
44,299 |
37,669 |
|
6 |
150,144 |
51,911 |
45,691 |
|
7 |
176,201 |
59,233 |
53,669 |
|
8 |
201,303 |
66,099 |
61,363 |
|
9 |
224,874 |
72,403 |
68,596 |
|
10 |
246,540 |
78,090 |
75,249 |
|
11 |
266,102 |
83,144 |
81,262 |
|
12 |
283,503 |
87,582 |
86,614 |
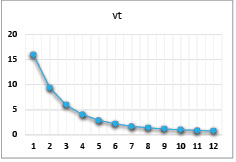
Рис. 19. Динамика выпуска при значениях параметров α = 0,86, β = 0,8, γ = 0,4
Таблица 22
(расчеты для параметров α =0,86, β =0,2, γ=0,6)
|
t |
PKt |
vt |
Dt |
|
1 |
0 |
16 |
0 |
|
2 |
23,158 |
10,647 |
10,240 |
|
3 |
15,241 |
7,510 |
8,435 |
|
4 |
10,654 |
5,568 |
5,873 |
|
5 |
7,841 |
4,308 |
4,309 |
|
6 |
6,031 |
3,458 |
3,306 |
|
7 |
4,816 |
2,863 |
2,635 |
|
8 |
3,971 |
2,436 |
2,170 |
|
9 |
3,366 |
2,120 |
1,837 |
|
10 |
2,922 |
1,882 |
1,593 |
|
11 |
2,588 |
1,700 |
1,409 |
|
12 |
2,332 |
1,557 |
1,269 |
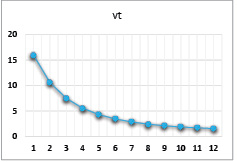
Рис. 20. Динамика выпуска при значениях параметров α = 0,86, β = 0,2, γ = 0,6
Таблица 23
(расчеты для параметров α = 0,86, β = 0,6, γ = 0,6)
|
t |
PKt |
vt |
Dt |
|
1 |
0 |
16 |
0 |
|
2 |
43,017 |
18,224 |
10,240 |
|
3 |
49,108 |
20,346 |
13,420 |
|
4 |
54,937 |
22,335 |
15,027 |
|
5 |
60,408 |
24,168 |
16,537 |
|
6 |
65,461 |
25,836 |
17,934 |
|
7 |
70,065 |
27,335 |
19,208 |
|
8 |
74,211 |
28,671 |
20,355 |
|
9 |
77,907 |
29,851 |
21,380 |
|
10 |
81,176 |
30,886 |
22,286 |
|
11 |
84,045 |
31,788 |
23,081 |
|
12 |
86,550 |
32,572 |
23,776 |
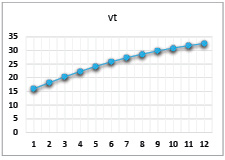
Рис. 21. Динамика выпуска при значениях параметров α = 0,86, β = 0,6, γ = 0,6
Таблица 24
(расчеты для параметров α = 0,86, β = 0,8, γ = 0,6)
|
t |
PKt |
vt |
Dt |
|
1 |
0 |
16 |
0 |
|
2 |
80,650 |
31,433 |
10,240 |
|
3 |
159,320 |
55,273 |
21,490 |
|
4 |
281,584 |
88,442 |
38,087 |
|
5 |
452,633 |
130,643 |
61,397 |
|
6 |
671,330 |
180,401 |
91,317 |
|
7 |
930,316 |
235,415 |
126,885 |
|
8 |
1217,741 |
293,036 |
166,503 |
|
9 |
1519,766 |
350,717 |
208,274 |
|
10 |
1822,934 |
406,318 |
250,331 |
|
11 |
2115,854 |
458,264 |
291,077 |
|
12 |
2390,047 |
505,554 |
329,309 |
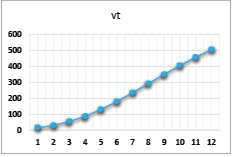
Рис. 22. Динамика выпуска при значениях параметров α = 0,86, β = 0,8, γ = 0,6
Выводы
Анализ эмпирических расчётов по динамической модели с учетом риска структуры капитала, алеющего на стоимость заемного финансирования затрат производственной сферы корпорации реального сектора экономики, продемонстрировал следующие закономерности:
- наибольшее влияние на анализируемую динамику оказывает риск структуры капитала: начиная со значения коэффициента финансового рычага 0,8 динамика финансового результата, несмотря на рост стоимости заемных средств, приобретает характер экспоненциального (с расширением горизонта планирования) роста. Особенно это характерно для предприятий с масштабом производства в диапазоне 0,8-0,83. Наоборот, для предприятий с большим масштабом (например, 0,86) эта закономерность не отмечается. Тем самым подтверждается гипотеза проф. Халикова М.А. о стратегических преимуществах производственных корпораций с масштабом производства, близких или равных 0,83;
- влияние масштаба производства на динамику товарного выпуска и результат в производственной сфере корпорации отмечено характером ее роста/падения (высокий/низкий);
- эндогенный параметр доли собственных инвестиций в рабочем капитале корпорации также оказывает о посредственное влияние на динамику выпуска товарной продукции и финансовый результат производственной сферы. Можно с уверенностью предполагать, что рассмотренная динамическая модель «настроена» на кратко- и среднесрочные интервалы планирования, у которых ведущая роль отводится объему и стоимости располагаемых предприятием активов, авансированных или прямо образующих его затраты, тогда как инвестиции в рабочий капитал-инструмент долгосрочной стратегии предприятия.
Библиографическая ссылка
Халиков М.А., Кулинченко Е.С., Струкова А.А. ДИНАМИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПРОИЗВОДСТВЕННОЙ СФЕРЫ ПРЕДПРИЯТИЯ С УЧЕТОМ РИСКА СТРУКТУРЫ РАБОЧЕГО КАПИТАЛА // Вестник Алтайской академии экономики и права. 2021. № 3-2. С. 239-253;URL: https://vaael.ru/ru/article/view?id=1636 (дата обращения: 11.03.2026).
DOI: https://doi.org/10.17513/vaael.1636