Значительную роль, особенно в военном деле, играют методы и модели распределения военных расходов при обеспечении мероприятий боевой подготовки войск (сил). Появление и становление методов и моделей прежде всего и было обусловлено потребностями военно-научных исследований, решением задач планирования военных операций (боевых действий) и анализа их эффективности. В современных условиях основными направлениями применения метода геометрической интерпретации задач линейного программирования в военном деле является оценивание эффективности применения вооружения по назначению, обеспечиваемо обоснованный выбор его тактико-технических характеристик и способов боевого применения; военно-экономическое оценивание качества вооружения и связанное с решением задач выбора оптимального варианта развития вооружения и научно обоснованного планирования в области военного строительства, научно обоснованного решения задач планирования боевых действий войск:
- прогнозирование возможного хода и исхода боевых действий;
- оценивание эффективности вариантов выполнения различных организационно-технических мероприятий в течение жизненного цикла образцов вооружения и т.д.
Владение аппаратом теории эффективности и исследования операций способствует повышению эффективности работы специалистов по обеспечению выбора вариантов действий, давших возможность наилучшим образом использовать ресурсы, выделяемые на выполнение разнообразных организационно-технических мероприятий, в том числе и мероприятий оборонного характера. Оно позволяет военному экономисту более качественно решать задачи обоснования в достаточно эффективные способы их применения по назначению, рациональным образом организовывать работу по распределению военных расходов, решать и многие другие военно-экономические проблемы и задачи, возникающие в практической деятельности.
Единый комплекс графоаналитического метода геометрической интерпретации задач линейного программирования исследуемых объектов и моделей для принятия решений, реализованных на базе современных технологий, составляет основу автоматизированных систем многовариантного анализа и прогнозирования характеристик сложных технических спотов, (Спот (англ. spot – «место, точка»)), а так же принятия рациональных решений по вариантам проектных разработок и способов применения этих систем по назначению математической модели объекта исследования, которые с требуемой точностью воспроизводят все процессы его функционирования от данных внешних воздействующих факторов, которые обеспечивают получение дополнительной к экспериментальным данным информации, необходимой для принятия соответствующих решений.
Разнообразие и сложность исследований современных технических систем обусловливают необходимость использования широкого диапазона катодов и средств научных исследований, начиная с классических и кончая современными методами и средствами, учитывающими программно-системный характер объекта исследования.
Это затрудняет подготовку специалистов в области исследований графоаналитического метода геометрической интерпретации задач линейного программирования в области военного применения. По-видимому, основным принципом которым необходимо руководствоваться при отборе изучаемых методов исследований, следует считать принцип отбора информации по признакам их результативности и экономичности частоты применения полноты охвата решаемых задач и степени адекватности этим задачам, точности и достоверности получаемых экономических результатов степени учета свойства системности объекта исследования.
Данный метод является универсальным методом исследований. Наличие модели, адекватной в определенном смысле реальному объекту, дает возможность переносить исследование объекта на модель и затем по характеристикам модели делать вывода о характеристиках объекта-оригинала посредством умозаключения по аналогии. Особенно результативным при исследовании сложных систем оказалось имитационное моделирование, основанное на применении современных технологий, воспроизводящих процессы функционирования систем с сохранением их логической структуры и последовательности чередования во времени происходящих событий.
Конкретизацией графоаналитического метода геометрической интерпретации задач линейного программирования является применение специальных приемов (частных методов) исследования макроэкономических процессов и достигнутых результатов военно-экономической деятельности. К числу основных методов относятся сравнение, группировка, элиминирование, балансовый, графический, экономико-математическое моделирование.
Действительно, военную экономику и военно-экономический анализ роднит единство объекта изучения – система действий по экономическому обеспечению военной безопасности страны. С другой стороны, военно-экономический анализ вполне логично рассматривать как специфическую разновидность общей теории и практики экономического анализа различных видов хозяйственной деятельности (в военной сфере военно-хозяйственной деятельности) [1].
За многие десятилетия анализ хозяйственной деятельности разработан достаточно фундаментально, изданы работы по общей теории анализа, созданы методики анализа финансового состояния и в целом хозяйственной деятельности промышленных предприятий [10].
Объекты непроизводственной сферы, анализа не только предприятий, но и отрасли народного хозяйства, виды и направления деятельности, [9] нуждаются в изучении с применением графоаналитического метода геометрической интерпретации задач линейного программирования, которые более глубоко раскроют систему расходов хозяйственной деятельности. Владение данными навыками позволяет в условиях конкурентной экономики не только строго исполнять директивные указания, но и оценивать конкурентоспособные варианты организации деятельности, уметь выбирать оптимальные решения.
Знание методов и методик линейного программирования, прописанные профессором Викуловым С.Ф. в военно-экономическом анализе, дают возможность специалистам выбирать наиболее экономичные варианты в различных областях: в войсковой сфере деятельности при решении задач тылового обеспечения и организации боевой подготовки, при оптимизации программ вооружения и государственного оборонного заказа, при формировании путей военного строительства и реформы Вооруженных Сил Российской Федерации, других войск и войсковых формирований, входящих в военную организацию государства. В военной сфере конкурентный подход проявляется при оптимизации программ развития ВВТ, военно-экономическом обосновании тактико-технических характеристик ВВТ, проведении конкурсов на поставку продукции для государственных нужд, оптимизации военной деятельности и совершенствовании механизма финансово-экономического обеспечения военного строительства [5].
Как и все методы математического программирования, графоаналитический метод геометрической интерпретации задач линейного программирования применяется для обоснования распределения сил, средств и других ресурсов по задачам или объектам [6].
Предметом графоаналитического метода геометрической интерпретации задач линейного программирования являются специфические военно-экономические отношения по поводу наиболее эффективных путей использования материальных, трудовых и финансовых ресурсов, выделяемых из федерального бюджета для решения задач обеспечения военной безопасности. Его можно использовать как инструмент обоснования способов применения сил и средств в военном деле, как инструмент параметрической оптимизации проектируемых расходов и т.д., когда показатель расходов и ограничения являются линейными или могут быть сведены к линейным зависимостям от искомых величин. Рассмотрим простейший случай, когда задача линейного программирования содержит всего две переменные [7]:
F(x1, x2) = c1x1 + c2x2 → max;
a11x1 + a12x2 ≤ b1,
… (1)
am1x1 + am2x2 ≤ bm ,
x1 ≥ 0, x2 ≥ 0
Вводим на плоскости декартову прямоугольную систему координат x1 O x2 и сопоставим каждой паре чисел (x1, x2) точку на плоскости с координатами x1 и x2. Каждое ограничение задачи (1) вида ai1x1 + ai2x2 ≤ bi i = 1…m, задает в системе координат x1 O x2, полуплоскость (рисунок), включающую и граничную прямую ai1x1 + ai2x2 = bi. Общая часть (пересечение) всех m, полуплоскостей, лежашая в первой четверти x1 ≥ 0, x2 ≥ 0 координатной плоскости x1 O x2, является геометрическим образом допустимого множества ωx задачи линейного программирования (областью допустимых решений задачи). Допустимая область может быть пустой (ограничения несовместимы, и задача не имеет решения), представлять собой некоторый многоугольник (рисунок), может быть неограниченной в направлении возрастания целевой функции (задача (2) не имеет решения). Оптимальными являются те точки допустимой области, координаты которых доставляют целевой функции наибольшее значение.
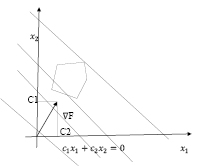
Графическое представление процедуры нахождения решения задачи линейного программирования в пространстве двух переменных
Линейная функция F(x1, x2) = c1x1 + c2x2 принимает одно и то же значение a во всех точках прямой c1x1 + c2x2 = a, где a – некоторое действительное число. Урaвнeние этой прямой, называемой линией уровня функции F(x1, x2) = c1, можно записать в следующем виде [8]:
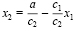 (2)
(2)
Из выражения (2) следует, что угловой коэффициент этой прямой равен c1/c2 и не зависит от a. Если мы будем изменять величину a, то прямая (3.13) будет передвигаться, оставаясь параллельной самой себе (угловой коэффициент, определявший угол наклона прямой к осям координат, не изменяется). Таким образом, различным значениям a соответствуют разные прямые на плоскости, но все они параллельны между собой. Считая a параметром, получаем семейство параллельных прямых – линий уровня функции F(x1, x2) = c1x1 + c2x2.
Значения a (а значит, и значения функции F = c1x1 + c2x2 возрастают неограниченно, если перемещать прямую c1x1 + c2x2 = a в направлении градиента функции F(x1, x2):
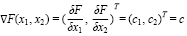 (3)
(3)
т.е. в направлении нормали к линии уровня функции F(x1, x2). Следовательно, чтобы найти оптимальные точки допустимого множеств, в которых функция F(x1, x2) принимает наибольшее значение, нужно перемешать прямую c1x1 + c2x2 = a в направлении вектора c = (c1, c2)T, начиная с какого-нибудь фиксированного положения, при котором она пересекается с допустимой областью, до тех пор, пока она не станет пересекаться с ней (рисунок). Пересечение допустимой области с линией уровня в том ее положении, когда дальнейшее перемещение дает пустое пересечение, и будет множеством оптимальных точек задачи линейного программирования.
Анализируя рассмотренный графоаналитический метод решения задачи линейного программирования, можно заметить следующие закономерности:
- оптимальное решение, если оно существует, не может лежать внутри области допустимых решений, а может находиться только в ее границе;
- решение может быть и не единственным. Действительно, если линия уровня целевой функции параллельна той стороне многоугольнике допустимых, решений, где достигается максимум F, то он достигается не в одной точке, а во всех точках этой стороны;
- задача может и не иметь решения даже в случае, когда существует непустая область допустимых решений. Это бывает тогда, когда в направлении роста целевой функции (в задаче на максимум) допустимая область не ограничена;
- решение задачи линейного программирования, максимизирует функцию F (оптимальное решение), всегда достигается в одной из вершин многоугольника допустимых решений (если оно достигается на целой стороне, то оно же достигается и каждой из вершин через которые проходит эта сторона);
- решение, лежащее в одной из вершин допустимой области, называется опорным решением, а сама вершина – опорной точкой;
- для того, чтобы найти оптимальное решение, в принципе достаточно перебрать все вершины допустимой области (опорные точки) и выбрать из них ту, где функция F достигает максимума.
Графоаналитический метод, основанный на геометрической интерпретации задачи линейного программирования, применяется при решении задач двумерного пространства. В трехмерном пространстве этот метод также принципиально может быть применен, однако его практическая реализация затруднена из-за необходимости пространственных (а не на плоскости) графических построений. Задачу пространства размерности больше трех представить графически вообще невозможно. Поэтому для нахождения решения задачи линейного программирования в общем случае применяются не геометрические, а алгебраические методы.
Автоматизированная система анализа и прогнозирования, предназначенная для повышения эффективности исследований при научно-техническом сопровождении сложных объектов, должна строиться в соответствии с принципами модульности, расширяемости и машинной независимости ее программного обеспечения. Это позволяет, при необходимости, изменять структуру системы анализа и прогнозирования, подстраивая ее под решаемую задачу, осуществлять быструю замену используемых модулей новыми при совершенствовании системы, непрерывно пополнять ее новыми программными средствами. Разработка автоматизированной системы анализа и прогнозирования требует затрат значительных средств и времени.
Таким образом эта система должна создаваться для решения задач исследований, т.е. она должна быть инструментов постоянного его анализа.
Библиографическая ссылка
Башашкина Г.Ю. ГРАФОАНАЛИТИЧЕСКИЙ МЕТОД ГЕОМЕТРИЧЕСКОЙ ИНТЕРПРЕТАЦИИ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ ПРИ ПРИМЕНЕНИИ В ВООРУЖЕННЫХ СИЛАХ // Вестник Алтайской академии экономики и права. 2020. № 12-2. С. 223-227;URL: https://vaael.ru/ru/article/view?id=1500 (дата обращения: 08.03.2026).
DOI: https://doi.org/10.17513/vaael.1500

