Введение
Традиционная модель планово-производственной задачи, широко представленная в публикациях отечественных исследователей (например, Д. Безухова, Е. Дорохиной, Б. Лагоши, А. Мищенко, М. Халикова [5, 10, 12, 14]), отличается детерминированным характером и может быть использована в условиях невысокой изменчивости товарных, материальных и финансовых рынков. В случае нестабильных рынков, характеризующихся высокой изменчивостью спроса и цен, сфера приложения статичных моделей ограничивается, как правило, краткосрочным интервалом планирования.
С другой стороны, для моделей «рюкзачного» типа, к которым относится и указанная модель, эффективным способом учета динамики экзогенных параметров является подход, основанный на использовании в моделях альтернативного доходности критерия рыночного риска производственной программы.
Методологическая основа исследования
Методологическую основу работы составили труды отечественных и зарубежных ученых и исследователей-практиков по проблемам:
– экономико-математического моделирования производственной деятельности предприятия в условиях стабильной макроэкономической среды [2, 4, 10, 12];
– экономико-математического моделирования производственной деятельности предприятия в условиях изменчивой макроэкономической среды [5, 6, 14];
– построения моделей производственной функции предприятия в статичном и динамическом вариантах [4, 6, 9];
– оценки и учета затрат на производство машиностроительной продукции в рамках управленческого учета и сегментарной отчетности [1];
– построения моделей и выбора численных алгоритмов задач линейной и нелинейной оптимизации в сфере моделирования производственных и инвестиционных программ на уровне предприятий и производственных комплексов [3, 7];
– оценки и управления риском производственных предприятий и бизнес-единиц [8, 11, 13-18];
– построения моделей производственной функции предприятия в статичном и динамическом вариантах [7, 8, 15];
– институциональных преобразований в экономике хозяйствующих субъектов и инициируемых ими особенностей внутрифирменной деятельности российских промышленных предприятий на этапах завершения рыночных реформ [13, 14, 17, 19].
Цель и задачи исследования связаны с разработкой и адаптацией моделей и методов выбора оптимальной производственной программы предприятия с учетом дополнительного ограничения на допустимый риск.
Результаты исследования и обсуждение
В теории портфеля под риском понимается отклонение доходности портфеля от планируемого значения. Несомненным достоинством этого подхода, подтвержденным экономической практикой, начиная с момента публикации работы Г. Марковица, является удовлетворительная точность управленческих решений, принимаемых на основе информации о изменении экзогенных параметров за достаточно непродолжительный период наблюдений.
Рассмотрим один из возможных подходов к учету риска производственной программы в модели выбора оптимального варианта производственной деятельности предприятия.
Введем следующие обозначения:
Т – число временных интервалов, на которых фиксировались значения доходности (прибыльности) изделий производственной программы;
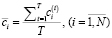 – средний за период наблюдений удельный маржинальный доход производства и реализации ед. продукции вида i;
– средний за период наблюдений удельный маржинальный доход производства и реализации ед. продукции вида i;
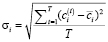 – дисперсия доходности продукции i-го вида за период наблюдений;
– дисперсия доходности продукции i-го вида за период наблюдений;
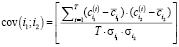 – ковариация доходностей продукции видов i1 и i2 (
– ковариация доходностей продукции видов i1 и i2 (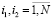 ) за период наблюдений;
) за период наблюдений;
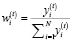 – доля продукции i-го вида в производственной программе в периоде t;
– доля продукции i-го вида в производственной программе в периоде t;
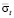 – пороговое (допустимое) значение риска производственной программы для периода t.
– пороговое (допустимое) значение риска производственной программы для периода t.
В этих обозначениях ограничение на риск производственной программы может быть представлено неравенством:
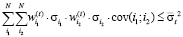 (3.1)
(3.1)
или
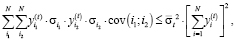 (3.1')
(3.1')
а в записи критерия следует учитывать не прогнозируемую, а среднюю (за период наблюдений) доходность изделий производственной программы:
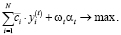 (2.1'')
(2.1'')
Включение в модель (2.1''), (2.15'), (2.18'), (2.23'), (2.25), (2.26') ограничения (3.1) переводит ее в класс задач нелинейной дискретной оптимизации большой размерности. Как известно, эти задачи относятся к NP-полным, отличающимся отсутствием универсальных численных методов поиска оптимального решения. В связи с этим используются методы, учитывающие специфику постановки задачи или особенности ее математической формализации.
Рассмотрим задачу оптимизации производственной деятельности предприятия с учетом ограничения на риск производственной программы в непрерывной постановке:
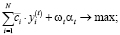 (1)
(1)
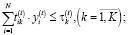 (2')
(2')
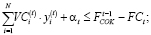 (3)
(3)
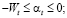 (4)
(4)
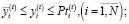 (5)
(5)
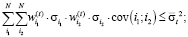 (6)
(6)
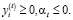 (7)
(7)
Отметим, что в модели (1)-(7) функционал и ограничения являются выпуклыми, дважды дифференцируемыми функциями, то открывает возможность использования в численной процедуре оптимизации метода множителей Лагранжа.
Параметрическое представление «затраты-выпуск» и задачи выбора производственной стратегии предприятия.
Составим функцию Лагранжа 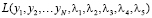 :
:
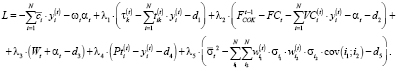 (3.2)
(3.2)
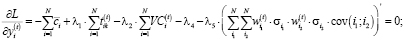 (8)
(8)
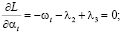 (9)
(9)
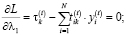 (10)
(10)
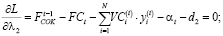 (11)
(11)
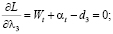 (12)
(12)
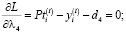 (13)
(13)
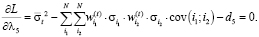 (14)
(14)
Согласно теореме Куна-Таккера: λi•di = 0.
Если 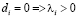 – ресурс дефицитен
– ресурс дефицитен
Если 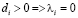 – ресурс недефицитен
– ресурс недефицитен
Опишем генерируемую ПФ с использованием следующих обозначений: 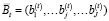 – вектор ограничений,
– вектор ограничений, 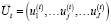 – вектор двойственных оценок задачи (1)–(7).
– вектор двойственных оценок задачи (1)–(7).
Представим функцию «выпуск- затраты» в виде:
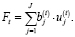 (15)
(15)
Модель (1)–(7) формирования производственной стратегии предприятия и построенная с использованием множителей Лагранжа функция «затраты-выпуск» (15) открывают перспективы решения следующих задач:
– анализ эффективности использования собственного и заёмного капиталов с учётом запланированного экономического результата производственной деятельности;
– определение норм замены ресурсов при планировании деятельности предприятия;
– определение изменения валового дохода при изменении принимаемого риска в финансовой и производственной сферах деятельности.
Продемонстрируем подходы к решению перечисленных задач.
Обозначим предельную норму замены i-го фактора j-ым как Rij. Она обратно пропорциональна предельным отдачам факторов:
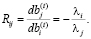 (16)
(16)
Однако на практике в расчетах замены факторов необходимо последние группировать в однородные классы, например, «заемные – собственные средства».
В этом случае можно рассчитать показатели нормы их замены:
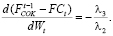 (17)
(17)
В свою очередь, полученное соотношение дает возможность оценить взаимозависимость между заёмным и собственным финансированием производственной деятельности предприятия и сформировать кредитную политики предприятия.
Для проведения ретроспективного анализа экономического результата необходимо рассчитать прирост экономического эффекта, который может быть получен в результате роста составляющих производственного капитала:
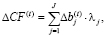 (18)
(18)
где ΔCF(t) – прирост денежного потока;
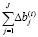 - прирост факторов.
- прирост факторов.
Практические расчеты вариантов производственных программ с учетом риска.
Расчеты, связанные с выбором оптимального варианта производственной программы предприятия с учетом риска, проводились на базе ФГУП «НИИЭМП».
В рамках конверсии одноименное научно-производственное объединение перешло на выпуск пользующихся спросом приборов для топливно-энергетического комплекса, автомобильной электроники и школьное оборудование.
В настоящее время предложена концепция развития института на ближайшие десять лет, которая включает разработку нового поколения приборов в интересах естественных монополий и собственных нужд, связанных с модернизацией метрологической и испытательной базы.
С целью увеличения объемов производства до уровня предполагаемого спроса, а также для расширения ассортимента выпускаемой продукции принято решение о привлечении заемного финансирования.
При рассмотрении задачи оптимального управления заемным капиталом предполагалось, что цена изделия, затраты на производство продукции, спрос и др. параметры являются заранее известными величинами. Однако в действительности эти параметры распределены по случайному закону. В связи с этим особый интерес представляют модели стохастической оптимизации.
Как и выше, риск производственной программы предлагается оценивать дисперсией маржинального дохода.
Предположим, что маржинальный доход ед. реализованной продукции i-го вида является дискретной случайной величиной, которая принимает значения с вероятностью, указанной в табл. 1.
Сформулируем двухкритериальную задачу о распределении кредитных ресурсов на максимум прибыли и минимум риска портфельных закупок материальных ресурсов.
Исходные данные приведены в табл. 2 (производственная база предприятия), в табл. 3 и 4 (затраты ресурсов на производство ед. продукции), и в табл. 5 (стоимость ед. ресурса). Исходя из требования возвратности кредита в 2 000 000 руб. и ставки 15 % годовых, минимальное значение маржинального дохода – 2 300 000 руб.
Задача минимизации риска производственной программы при ограничении на доходность представлена ниже – объемами выпускаемой продукции (табл. 6) и производственных ресурсов производства (табл. 7).
Из данных табл. 7 следует, что в условиях неопределенности следует отказаться от производства изделия К427ПА5Т, что связано с высокими удельными затратами и недостаточностью кредита.
Таблица 1
|
Наименование изделия |
МД с вероятностью 0,69 |
МД с вероятностью 0,04 |
МД с вероятностью 0,57 |
МД с вероятностью 0,23 |
|
НР1-17 |
255,93 |
276,4 |
253,37 |
273,64 |
|
НР1-22 |
231,84 |
250,39 |
229,52 |
247,88 |
|
НР1-33 |
243,28 |
262,74 |
240,85 |
260,11 |
|
НР1-43 |
240,81 |
260,07 |
238,4 |
257,47 |
|
НР1-53 |
900,48 |
972,52 |
891,48 |
962,79 |
|
НР1-54 |
335,84 |
362,71 |
332,48 |
359,08 |
|
НР1-55 |
160,78 |
173,64 |
159,17 |
171,91 |
|
НР1-60 |
386,51 |
417,43 |
382,64 |
413,26 |
|
313НР310-311 |
248,33 |
268,2 |
245,85 |
265,51 |
|
ТРП |
175,52 |
189,56 |
173,76 |
187,67 |
|
427ПА2 |
1512,3 |
1633,28 |
1497,18 |
1616,95 |
|
427ПА4 |
1860,99 |
2009,87 |
1842,38 |
1989,77 |
|
К427ПА5Т |
1816,26 |
1961,56 |
1798,1 |
1941,95 |
Таблица 2
|
Технологические пределы (операции) |
Время загрузки, (час) |
Время эффективного использования, (час) |
Количество, (ед.) |
|
УВН71-ПЗ |
0,23 |
13867 |
1 |
|
Термокамера |
0,8 |
13867 |
3 |
|
Термостат |
0,22 |
13867 |
3 |
|
Установка сварки |
0,11 |
13867 |
3 |
|
Установка совмещения и экспонирования |
0,1 |
13867 |
5 |
Таблица 3
|
Производственный фактор |
Затраты по изделиям (кг, м) |
|||||||
|
НР1-17 |
НР1-22 |
НР1-33 |
НР1-43 |
НР1-53 |
НР1-54 |
НР1-55 |
НР1-60 |
|
|
Кермет К20С |
1,7E-05 |
0,00001 |
1,5E-05 |
1,7E-05 |
5E-06 |
7E-06 |
3E-06 |
9E-07 |
|
Дозированные гранулы алюминия |
3,2E-05 |
1,9E-05 |
2,9E-05 |
3,2E-05 |
9,6E-06 |
1,4E-05 |
5,7E-06 |
1,7E-06 |
|
Краска черная МА-514 |
0,00004 |
2,4E-05 |
0,00004 |
0,00004 |
0,00002 |
0,00002 |
0 |
0 |
|
Лак ЭП-730 |
0,00024 |
0,00024 |
0,00024 |
0,0001 |
0,0001 |
0 |
0,0001 |
|
|
Паста У2 |
3,7E-05 |
6,1E-06 |
6,1E-06 |
3,7E-05 |
0,00037 |
0,00026 |
0,00015 |
0 |
|
Катализатор № 28 |
8E-07 |
1,2E-06 |
1,2E-06 |
8E-07 |
8E-06 |
8E-06 |
5E-06 |
3E-06 |
|
Гидрофобизир. жид. 136-41 |
8E-07 |
1,2E-06 |
1,2E-06 |
8E-07 |
8E-06 |
8E-06 |
5E-06 |
3E-06 |
|
Толуол |
1,1E-05 |
0,00004 |
1,1E-05 |
0,00011 |
0,00011 |
7,9E-05 |
4,5E-05 |
|
|
Алюминиевая проволока АК 0,9 ПМ-50 |
0 |
0,00024 |
0,00047 |
2,6E-06 |
0,00069 |
0,00092 |
0,00572 |
0,00015 |
Таблица 4
|
Производственный фактор |
Затраты по изделиям (кг, м) |
||||
|
313НР310-311 |
ТРП |
427ПА2 |
427ПА4 |
К427ПА5Т |
|
|
Кермет К20С |
0,00004 |
0,0000045 |
0,000038 |
0,000038 |
0,000227 |
|
Дозированные гранулы алюминия |
0,000083 |
0 |
0,000073 |
0 |
0,000125 |
|
Краска черная МА-514 |
0,00005 |
0 |
0,0000384 |
0,0000384 |
0 |
|
Лак ЭП-730 |
0 |
0 |
0,0002 |
0,0002 |
|
|
Паста У2 |
0,000175 |
0 |
0,0000061 |
0,0000061 |
0,000148 |
|
Окончание табл. 4 |
|||||
|
Производственный фактор |
Затраты по изделиям (кг, м) |
||||
|
313НР310-311 |
ТРП |
427ПА2 |
427ПА4 |
К427ПА5Т |
|
|
Катализатор № 28 |
0 |
0 |
0,0000012 |
0,0000012 |
0,0000032 |
|
Гидрофоби-зир. жид. 136-41 |
0 |
0 |
0,0000012 |
0,0000012 |
0,0000454 |
|
Толуол |
0 |
0 |
0,00004 |
0,00004 |
0,0000454 |
|
Алюминиевая проволока АК 0,9 ПМ-50 |
0 |
0 |
0,001188 |
0,0000008 |
0,24 |
|
Нефрас - С 50/170 |
0 |
0 |
0 |
0 |
0,00033 |
|
Припой ПОС-61 |
0,000143 |
0,002 |
0,000182 |
0 |
0 |
|
Канифоль сосновая |
0,000001 |
0,000001 |
0,000001 |
0,000001 |
0,000001 |
|
Подложка ситалловая СТ 50-1-1-0,6 |
0,183 |
0,044 |
0,183 |
0,183 |
0,4036 |
|
Проволока кр.Зл. 999,9-0,04 |
0,0000016 |
0 |
0 |
0 |
0 |
|
Аноды серебряные |
0,0000394 |
0 |
0 |
0 |
0 |
|
Дицианоар-гентат калия |
0,0000727 |
0 |
0 |
0 |
0 |
|
Прессматериал АГ-4В |
0,00293 |
0 |
0 |
0 |
0 |
|
Смола эпоксидная ЭД- 20 |
0,000125 |
0 |
0,000049 |
0,000052 |
0,000021 |
|
Пластификат ДБФ |
0,000012 |
0 |
0 |
0 |
0 |
|
Полиэтилен-полиамин |
0,000012 |
0 |
0 |
0 |
0 |
|
Ситалл ЭА-1-Б |
0,000125 |
0 |
0 |
0 |
0 |
|
Компаунд КЭ-14В |
0,000312 |
0 |
0 |
0 |
0 |
|
Лента Л63 ДПрНТ 0,15 |
0,00204 |
0 |
0 |
0 |
0 |
|
Проволока медная 0 0,6 |
0 |
0,003 |
0 |
0 |
0 |
|
Кристалл Б572ПП1-4 |
0 |
0 |
1 |
0 |
1 |
|
Никель НПА-1 |
0 |
0 |
0,000179 |
0 |
0 |
|
Гелий |
0 |
0 |
0 |
0 |
0,002 |
Таблица 5
|
Наименование ресурса |
Цена (руб.) |
|
Кермет К20С |
1534 |
|
Дозированные гранулы алюминия |
825 |
|
Краска черная МА-514 |
4000 |
|
Лак ЭП-730 |
305 |
|
Паста У2 |
349,6 |
|
Гидрофобизир. жид. 136-41 |
600 |
|
Толуол |
144,27 |
|
Алюминиевая проволока АК 0,9 ПМ-50 |
0,85 |
|
Нефрас - С 50/170 |
55,6 |
|
Припой ПОС-61 |
351,69 |
|
Канифоль сосновая |
150 |
|
Подложка ситалловая СТ 50-1-1-0,6 |
85 |
|
Проволока кр.Зл. 999,9 - 0,04 |
1463,95 |
|
Аноды серебряные |
18,19 |
|
Дицианоаргентат калия |
16,65 |
|
Прессматериал АГ-4В |
250 |
|
Смола эпоксидная ЭД-20 |
149,05 |
|
Пластификат ДБФ |
261 |
|
Полиэтиленполиамин |
106,6 |
|
Ситалл ЭА-1-Б |
5000 |
|
Компаунд КЭ-14В |
6058 |
|
Лента Л63 ДПрНТ 0,15 |
296,61 |
|
Проволока медная 0 0,6 |
285 |
|
Кристалл Б572ПП1-4 |
248,18 |
|
Никель НПА-1 |
932,2 |
|
Гелий |
712,5 |
Таблица 6
|
Наименование изделия |
Объем выпуска (шт.) |
|
НР1-17 |
457 |
|
НР1-22 |
794 |
|
НР1-33 |
350 |
|
НР1-43 |
340 |
|
НР1-53 |
375 |
|
НР1-54 |
802 |
|
НР1-55 |
3678 |
|
НР1-60 |
152 |
|
313НР310-311 |
337 |
|
ТРП |
327 |
|
427ПА2 |
195 |
|
427ПА4 |
52 |
|
К427ПА5Т |
0 |
Таблица 7
|
Наименование ресурса |
Объем закупки (ед.) |
|
Кермет К20С |
71 |
|
Дозированные гранулы алюминия |
39 |
|
Краска черная МА-514 |
187 |
|
Лак ЭП-730 |
15 |
|
Паста У2 |
426 |
|
Катализатор № 28 |
188 |
|
Толуол |
28 |
|
Алюминиевая проволока АК 0,9 ПМ-50 |
6 |
|
Нефрас-С 50/170 |
400 |
|
Припой ПОС-61 |
400 |
|
Окончание табл. 7 |
|
|
Наименование ресурса |
Объем закупки (ед.) |
|
Канифоль сосновая |
16 |
|
Подложка ситалловая СТ 50-1-1-0,6 |
7 |
|
Проволока кр.Зл. 999,9-0,04 |
125 |
|
Аноды серебрянные |
125 |
|
Дицианоаргентат калия |
1 |
|
Прессматериал АГ-4В |
1 |
|
Смола эпоксидная ЭД-20 |
2 |
|
Пластификат ДБФ |
2 |
|
Полиэтиленполиамин |
12 |
|
Ситалл ЭА-1-Б |
5 |
|
Компаунд КЭ-14В |
1 |
|
Лента Л63 ДПрНТ 0,15 |
1 |
|
Проволока медная 0 0,6 |
2 |
|
Кристалл Б572ПП1-4 |
2 |
|
Никель НПА-1 |
200 |
|
Гелий |
200 |
Ожидаемый валовый маржинальный доход, генерируемый в производственной сфере предприятия в условиях риска, составляет 2,3 млн руб., что заметно ниже результата, полученного для условий стабильной рыночной среды.
Однако даже и для случая недетерминированных экзогенных параметров существует производственная программа, реализуемая с привлечением заемных средств.
Заключение
В работе представлено описание инструментария экономико-математических моделей и методов выбора оптимального по критерию валового маржинального дохода и с учетом производственно-технологических, финансово-ресурсных, рыночных и рисковых ограничений варианта производственной программы предприятия. Предложен оригинальный подход к моделированию функции «затраты-выпуск», основанный на использовании в качестве двойственных оценок ограничений по производственным факторам и допустимому риску актуальных значений множителей Лагранжа, получаемых при решении соответствующей нелинейной задачи выпуклого программирования. Практическая ценность предложенных подхода и методов оптимизации заключается в возможности прогнозирования дохода, получаемого в производственной сфере предприятия, при изменении уровней внешних и внутренних рисков.
Библиографическая ссылка
Максимов Д.А. МОДЕЛИРОВАНИЕ ПРОИЗВОДСТВЕННОГО СЕГМЕНТА ПРЕДПРИЯТИЯ С УЧЁТОМ РИСКА ПРОИЗВОДСТВЕННОЙ ПРОГРАММЫ // Вестник Алтайской академии экономики и права. 2020. № 6-2. С. 262-270;URL: https://vaael.ru/ru/article/view?id=1192 (дата обращения: 01.01.2026).
DOI: https://doi.org/10.17513/vaael.1192

