Научный журнал

Вестник Алтайской академии экономики и права

Print ISSN 1818-4057

Online ISSN 2226-3977

Перечень ВАК

Статья посвящена исследованию инновационной деятельности предприятий и построению модели оценки эффективности внедрения инноваций в производство. Основной задачей является определение степени влияния на экономическую эффективность тех факторов, воздействие которых наиболее существенно. Достижению поставленной цели поможет использование многомерного статистического анализа, т.е. применение методов многомерного корреляционного анализа, позволяющего выявить взаимосвязи между факторами, и многомерного регрессионного анализа, в результате которого получаем многомерную модель исследуемого процесса.

ОАО «Денеб» – один из крупнейших заводов по выпуску безалкогольной продукции на Северном Кавказе. С начала своего основания и по сегодняшний день он занимает лидирующие позиции на рынке.

Основными видами выпускаемой продукции предприяти являются безалкогольные напитки. Основными потребителями является Республика Дагестан и другие регионы России. Продукция выпускается в ПЭТ-бутылках объемом 1,25 л., 0,5 л., 5,0 л., стекло – бутылках объемом 0,33 л, 0,5 л.

Инновации на предприятии в основном носят продуктовый характер.

Они представлены следующими инновационными продуктами:

1. Функциональные напитки («Шиповник», «Курага», «Фейхоа», «Кизил», «Гранат»).

2. Напитки «Диет».

3. Запуск новой линии и ввод ее в действие.

Исследованию подлежит результат внедрения выше перечисленных инноваций в производстве. То есть, необходимо определить экономическую эффективность этого внедрения.

Для этой цели проанализированы данные отчетов ОАО «Денеб» за пять лет выбранного периода. Из множества показателей, оказывающих влияние на экономическую эффективность, выделены наиболее важные, которые будут составлять перечень факторов, включаемых в модель. Для учета влияния всех факторов предпочтительней построить многофакторную модель линейного типа, что обеспечит возможность проследить долю воздействия каждого из факторов.

Проанализировав деятельность предприятия, можно сделать вывод о том, что для построения модели целесообразно в качестве факторов использовать следующие показатели:

– прибыль;

– инвестиции в инновации (средства, направляемые на внедрение инноваций);

– затраты на ресурсы;

– трудовые ресурсы предприятия;

– отчисления за негативное воздействие на окружающую среду.

Далее строим многофакторную модель, содержащую пять факторов:

X1 – прибыль;

X2 – инвестиции в инновации (средства, направляемые на внедрение инноваций);

X3 – затраты на ресурсы;

X4 – трудовые ресурсы предприятия;

X5 – отчисления за негативное воздействие на окружающую среду.

Количественным показателем экономической эффективности является прибыль, следовательно, целесообразно обозначить как Y, т.е. как результирующий показатель.

Данные по этим показателям представлены в таблице 1.

Таблица 1

Проведем корреляционный анализ. Основная задача корреляционного анализа состоит в оценке корреляционной матрицы генеральной совокупности по выборке и определении на ее основе оценок частных и множественных коэффициентов корреляции и детерминации.

Парный (частный) коэффициент корреляции характеризует тесноту линейной зависимости между двумя переменными соответственно на фоне действия (при исключении влияния) всех остальных показателей, входящих в модель. Они изменяются в пределах от -1 до +1, причем чем, ближе коэффициент корреляции к +1, тем сильнее зависимость между переменными. Если коэффициент корреляции больше 0, то связь положительная, а если меньше нуля – отрицательная.

Множественный коэффициент корреляции характеризует тесноту линейной связи между одной переменной (результативной) и остальными, входящими в модель; изменяется в пределах от 0 до 1. Квадрат множественного коэффициента корреляции определяет множественный коэффициентом детерминации, характеризующий долю дисперсии одной переменной (результативной), обусловленной влиянием всех остальных (аргументов), входящих в модель.

По выборке определим оценки параметров генеральной совокупности, а именно: вектор средних (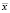), вектор средне-квадратических отклонений s и корреляционная матрица (R) порядка k:

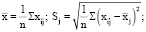
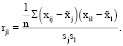
Получим, соответственно

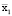= 185165195,8; 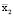= 491316279,8;

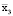= 283; 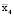= 7436,754;

Уср = 143707002,2

S1 = 162086741,8; S2 = 816721540,4;

S3 = 44,362146; S4 = 1058,673;

Sу = 110075370,1.

Среди полученных коэффициентов парной корреляции есть как положительные, так и отрицательные, что свидетельствует о наличии как прямой, так и обратной зависимости между факторами. Например, r12 = –0,32919 (характеризует взаимозависимость между прибылью и инвестициями в инновации). Также можно говорить о степени взаимной корреляции. Так, например, r32 = 0,098254 (характеризует взаимозависимость между трудовыми ресурсами и инвестициями в инновации) свидетельствует о слабой зависимости, в свою очередь, r04 = 0,609873 (характеризует взаимозависимости эффективности и экологического фактора) свидетельствует о достаточно сильной зависимости. Для нахождения матрицы частных коэффициентов корреляции необходимо найти алгебраические дополнения.

Далее, используя алгебраические дополнения по формуле

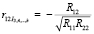
найдем частные коэффициенты корреляции (табл. 4).

Таблица 2

Матрица парных коэффициентов корреляции

Таблица 3

Матрица алгебраических дополнений

Таблица 4

Матрица частных коэффициентов корреляции

Для проверки значимости частных коэффициентов корреляции найдем rкр(β = 0,05, v = n – l – 2) = 0,378. Так как |r|<rкр, , то гипотезы Н0: ρ = 0 не отвергаются, т.е. предположение о равенстве нулю не противоречит наблюдениям. Но по данному критерию нельзя делать однозначные выводы. Для точности найдем интервальные оценки.

Определим интервальные оценки для коэффициентов корреляции при γ = 0,95. Для этого используем Z-преобразование Фишера и предварительно найдем интервальную оценку для Z из условия:

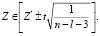
По таблице Z-преобразования Фишера получим таблицу значений Z’ для каждого частного коэффициента корреляции:

Таблица 5

И, далее, подставляя в формулу, получим интервальные оценки для Z. По таблице Z-преобразования найдем соответствующие интервальные оценки для частных коэффициентов корреляции:

r12∈[-0,582; 0,364]; r13∈[-0,054; 0,758]; r14∈[-0,392; 0,562]; r15∈[0,278; 0,87]; r23∈[-0,576; 0,374]; r24∈[-0,444; 0,514]; r25∈[-0,066; 0,754]; r34∈[-0,382; 0,568]; r35∈[-0,748; 0,078]; r45∈[-0,390; 0,562].

По проведенному анализу можно говорить о том, что все коэффициенты, кроме r15∈[0,278; 0,87] незначимы, так как нуль находится внутри интервала.

Вычислим множественные коэффициентов корреляции

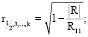
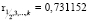; r2 = 0,56968;

r3 = 0,566859; r4 = 0,333501; r5 = 0,796927.

По значениям этих коэффициентов можно сделать следующие выводы:

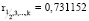– свидетельствует о том, что изменение прибыли на 74 % обусловлено влиянием остальных четырех факторов: инвестиций в инновации, затрат на ресурсы, трудовых ресурсов, экологического фактора. Выводы по остальным коэффициентам делаются аналогичным образом.

Проверим значимость по F-критерию. Найдем для каждого коэффициента Fнабл:

Fнабл =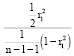

Fкр. (α = 0,05; v1 = 4; ν2 = 15) = 2,36, значит все коэффициенты кроме r4, значимы, т.к. Fнабл > Fкр, что свидетельствует о наличии линейной статистической зависимости между анализируемыми и остальными факторами за исключением фактора трудовых ресурсов.

Множественные коэффициенты детерминации соответственно равны:

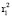= 0,534583, 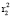= 0,324535,

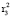= 0,321329, 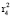= 0,111223,

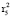= 0,635093.

Проведем регрессионный анализ.

Определим оценки параметров уравнения регрессии вида

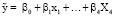
Для нахождения вектора оценок воспользуемся формулой

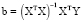
Пошагово перемножая матрицы, получим следующий вектор b: b = col(b0 = -504168863; b1 = -0,1410004; b2 = 0,03124761; b3 = 393523,838; b4 = 75008,9103).

Следовательно, уравнение регрессии будет иметь следующий вид:

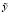= -504168863-0,1410004X1 +

+ 0,03124761X2 + 393523,838X3 +

+ 75008,9103X4.

Проверим значимость уравнения и коэффициентов регрессии.

1) Для проверки значимости уравнения регрессии используется статистика:

Fнабл = ,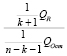

которая при выполнении гипотезы имеет F-распределение с (к + 1) и (n-k-1) степенями свободы, где Qост = 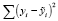; QR = ;

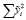В результате получим Fнабл = 3,874. Fкр(0,05; 6; 14) = 2,24. Так как Fнабл > Fкр, то гипотеза о равенстве всех коэффициентов нулю отвергается, т.е. хотя бы один коэффициент не равен нулю. Следовательно, уравнение значимо.

Перед проверкой значимости отдельных коэффициентов найдем несмещенную оценку остаточной дисперсии, которая равна:

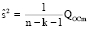
Найдем оценку ковариационной матрицы вектора b (табл. 6).

Таблица 6

Из статистического смысла ковариационной матрицы следует, что оценки дисперсий коэффициентов равны элементам главной диагонали матрицы.

Значимость коэффициентов регрессии можно проверить с помощью t-критерия:

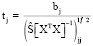
Tкр = 0,263, следовательно, значимыми можно считать коэффициенты b1 и b2, так как только t1 и t2 превышают критическое значение данного критерия. Проведем алгоритм пошагового регрессионного анализа и исключим из рассмотрения переменные Х3, Х4, Х5. Соответственно исключению подлежат коэффициенты b0, b3, b4, b5. Следовательно, уравнение регрессии будет иметь вид 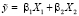. Исходными данными теперь являются показатели инвестиций в инновации и затрат на ресурсы.

Проделав аналогичные процедуры, как и в первый раз, на основании данных матриц по формуле МНК: 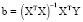найдем вектор оценок коэффициентов b: b = col(0,486119301; 0,041214565).

Вычислим tнабл: t1 = 27,86372869; t = 7,929776743.

Относительно критического значения они велики, следовательно, оба коэффициента значимы. Регрессионное уравнение имеет вид:

Y = 0,486X1 + 0,041X2.

То есть, основное влияние на эффективность оказывают инвестиции в инновации и затраты на ресурсы.

Коэффициенты же регрессионного уравнения показывают:

1. при изменении на единицу измерения инвестиций в инновации экономический эффект, в свою очередь, изменится на 0,486 единиц измерения.

2. Изменение на единицу измерения затрат на ресурсы повлечет изменение экономической эффективности на 0,0412 единиц.

На примере ОАО «Денеб» сделана попытка показать, как применение математических методов позволило для решения поставленной задачи построения модели оценки эффективности внедрения инноваций выделить совокупность тех факторов, изменение которых оказывает существенное влияние на величину экономической эффективности. На первом этапе отбираются факторы в общем определяющие экономическую эффективность. Между этими факторами существует определенная взаимосвязь, которая определяется с помощью корреляционного анализа. И его применение позволяет определить степень этой взаимосвязи.

Регрессионный анализ, на основе результатов корреляционного анализа, дает возможность построения модели, которая включает выделенные факторы, и позволяет, соответственно,исключить из модели те факторы, влияние которых несущественно и рассмотрение которых может отрицательно повлиять на качество модели.

В итоге получена модель, с меньшим числом факторов с наибольшим удельным весом во влиянии на результирующий показатель (экономическую эффективность).