В конце XX – начале XXI вв. в связи с усложнением организационной структуры компаний и на фоне масштабной трансформации технологий и экономической конъюнктуры рынков теория и практика инвестиционного анализа и проектирования столкнулись с проблемой достоверной оценки новых инструментов принятия решений. Ключевое значение получила парадигма стоимости активов, которая предполагает оценку эффективности бизнеса не по абсолютным показателям валовой или чистой прибыли. Возникшее понятие стоимости предполагает качественно новые подходы к оценке качества управления бизнесом в условиях быстрой смены технологических укладов, высокой изменчивости рынков готовой продукции и факторов производства, появления новых рисков, роста трансационных издержек на фоне укрупнения бизнеса. Изменившиеся экономические условия управления бизнесом предопределили появление качественно новых подходов к анализу и управлению проектами, особенно в венчурном бизнесе, где инвестиции оказывают непосредственное влияние на стоимость компании [1]. Традиционные и хорошо зарекомендовавшие себя подходы, математические модели и методы анализа инвестиционных проектов с использованием методологии чистой приведенной стоимости, основанной на анализе дисконтированных денежных потоков, принимаются экономическим сообществом с большой долей осторожности, т.к. они не позволяют должным образом учесть возможную гибкость менеджмента при адаптации управленческих решений в ответ на неожиданные изменения на рынке. Действительно, метод чистой приведенной стоимости предполагает наличие некоторого сценария изменения денежных потоков и пассивную приверженность менеджмента к изначально выбранной стратегии [2]. Однако реальные рынки характеризуются неопределенностью и значительными изменениями конъюнктуры даже в краткосрочной перспективе. По мере поступления новой информации и уменьшения неопределенности касательно рыночной ситуации менеджмент должен использовать гибкие инструменты оперативного реагирования и изменения первоначальной стратегии с целью извлечь выгоду из благоприятных будущих возможностей или уменьшить текущие потери.
Такая гибкость свойственна финансовым опционам, а в области инвестиционной оценки – стратегическим или реальным опционам. В связи с этим традиционные модели инвестиционного анализа могут быть дополнены, а в некоторых случаях заменены альтернативными подходами, например, методом оценки текущей стоимости опциона колл (пут) с использованием формулы Блэка-Шоулза-Мертона [2]. Эти подходы позволяют нивелировать указанные выше недостатки традиционных методов, но предполагают корректное использование включенных в них параметров и переменных, а главное, – предположений, на основе которых эти формулы выведены.
Напомним, что модель Блэка-Шоулза или Блэка-Шоулза-Мертона представляет собой математическую модель динамики финансового рынка, содержащего производные инвестиционные инструменты [3]. Это модель ценообразования опционов, используемая для предсказания тенденции изменения рыночной цены или дохода во времени, а также изменения стоимости финансовых инструментов, таких, например, как акции.
Рассмотрим вывод классической формулы – модели ценообразования опционов Ф. Блэка – М. Шоулза. Сделаем некоторые предположения.
Важнейшее заключается в том, что цена премии опциона испытывает дискретное логарифмическое блуждание:
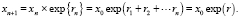 (1)
(1)
Если итоговая доходность через n торговых дней является случайным числом с распределением Гаусса r = μ + σε, то распределение цены опциона характеризуется логнормальным распределением:
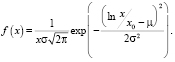 (2)
(2)
Получаем:
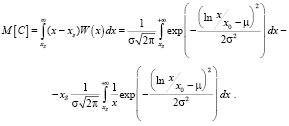 (3)
(3)
В первом интеграле (3) сделаем замену 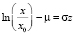 , получаем
, получаем
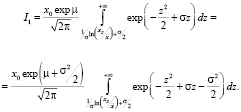 (4)
(4)
Заметим, что среднее значение (медиана) 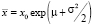 . Нижний придел объясняется эквивалентным равенством
. Нижний придел объясняется эквивалентным равенством 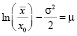 . Следовательно, выделяя полный квадрат последнем интеграле и заменяя z – σ = t, а также учитывая симметрию нормального распределения, наблюдаем, что этот интеграл преобразуется к виду:
. Следовательно, выделяя полный квадрат последнем интеграле и заменяя z – σ = t, а также учитывая симметрию нормального распределения, наблюдаем, что этот интеграл преобразуется к виду:
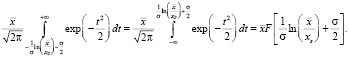 (5)
(5)
Во втором интеграле (3) делаем замену 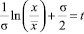 . Получаем на основе тех же суждений равенство:
. Получаем на основе тех же суждений равенство:
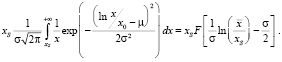 (6)
(6)
Объединяя оба интеграла, получим выражение:
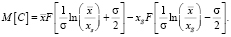 (7)
(7)
Здесь M[C] средняя цена call – опциона, 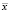 – средняя цена, F[y] – интегральная функция распределения нормального закона с единичной дисперсией и нулевым математическим ожиданием.
– средняя цена, F[y] – интегральная функция распределения нормального закона с единичной дисперсией и нулевым математическим ожиданием.
Если учитывать изменения стоимости во времени, то необходимо сделать провести уточнение выражения (7). Пусть актив на интервале Т оценен как 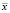 , а процентная ставка составляет величину υ, тогда сегодняшняя его стоимость
, а процентная ставка составляет величину υ, тогда сегодняшняя его стоимость 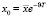 . Аналогично с ценой опциона:
. Аналогично с ценой опциона: 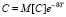 . В результате получим известную формула Ф. Блэка и М. Шоулса:
. В результате получим известную формула Ф. Блэка и М. Шоулса:
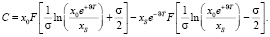 (8)
(8)
ЗФормула (8) ценообразования опционаи её аналоги произвели большой социальный резонанс, вызвали споры и восторженные отклики. Действительно, благодаря свойством нормального и логнормального распределений формула и выводится, и выглядит изящно. С течением времени представления о практической пользе этой формулы, например, для формирования оптимального портфеля, подверглись критике, стало очевидно, что, являясь вкладом в математическое моделирование процессов, протекающих на финансовых рынках, формула (8) не в полной мере адекватна рыночной практике: финансовые рынки- нестационарны, волатильность изменяется со временем, простое логарифмическое блуждание оказывается достаточно грубым приближением к реальности, непрерывная реструктуризация портфеля затруднена.
Тем не менее, модель (8) широко используется (часто с корректировками и исправлениями) участниками рынка опционов, при управлении рисками в страховании, торговле на фондовом рынке и инвестировании, находит широкое применение в практике анализа инвестиционных проектов при оценке капитальных вложений в разных отраслях: горнодобывающей, перерабатывающей, машиностроении и др.
Институциональные инвесторы широко используют модель (8) при составлении портфеля ценных бумаг, соответствующего их инвестиционным целям. Производные финансовые инструменты часто являются дешевым и эффективным способом изменения инвестиционного микса портфеля. Производные инструменты можно использовать для изменения воздействия портфеля на определенный риск. Например, в случае, когда портфельный менеджер входит в длинную позицию в фьючерсном контракте, это определяет такой же тип риска, как и владение базовой ценной бумагой: дешевле и эффективнее использовать фьючерсный контракт, чем покупать базовую ценную бумагу. Производные инструменты могут также обеспечивать защиту от падения путем покупки опционов на покупку или заключения короткой позиции в фьючерсном контракте.
Многие продукты, которые продаются розничным инвесторам в настоящее время, содержат встроенные опционы, и потребитель покупает пакет в виде полного контракта. Например, договоры страхования жизни и сбережений содержат встроенные производные инструменты. В США примером являются так называемые аннуитеты с индексом акций (определенная денежная сумма, которую ежегодно выплачивают кредитору в счет погашения полученного займа, включая проценты, зависящие от выбранного фондового индекса).
Эти продукты включают опционную функцию, которая позволяет клиенту извлекать выгоду из хорошей работы на фондовом рынке. Как правило, такие контракты будут содержать встроенный опцион колл в портфеле акций, например, на индекс S&P, они также гарантируют, что клиент получит минимальную норму прибыли независимо от того, как работает фондовый рынок [4]. Преимущество для потребителей заключается в том, что они участвуют на фондовом рынке, когда он преуспевает, и имеют гарантию базового возврата, когда рынок работает «плохо».
Подход Блэка-Шоулза-Мертона может быть экстраполирован на многие другие области оценки инструментов, относительно будущей стоимости которых имеется значительная неопределенность:
- страховые контракты и гарантии. В той или иной степени они обладают признаками опциона;
- принятие решений об инвестициях. В этой ситуации опционом является эффект от реализации проекта в условиях изменения конъюнктуры рынка. Чаще всего речь идет о таких крупных проектах, как переключение с одного источника энергии на другой (в случае, если значительно изменяются цены на газ или электричество), закрытие и повторное открытие производства (например, при падении цен на металлы и комплектующие) и др.;
- определение стоимости новых финансовых инструментов или оценка специфических активов по заказу клиента. Модель Блэка-Шоулза активно используется инвестиционными банками при решении этой задачи;
- реальные опционы. Речь идет о том, что собственный капитал компании может быть представлен в виде опциона-колл с учетом того, что собственник бизнеса в любой момент может его ликвидировать [5].
Логика реальных опционов основана тех же принципах, что и теория финансовых: реальный опцион, как и финансовый, создает значительную гибкость в оценке альтернатив для инвестирования. Анализ на основе реальных опционов позволяет определить, когда и в каком объеме необходимо выполнять конкретные капитальные вложения. Таким образом, процесс принятия решений, основанный на реальных опционах, является приближением к инвестированию и оценке в условиях высокой неопределенности и риска [6].
Ярким примером возможностей использования метода реального опциона является случай корпорации, рассматривающей покупку или продажу участков земли, содержащих месторождения золота. Если чистая приведенная стоимость (net present value, NPV) проектов по добыче золота оказывается положительной, компания начинает разработку соответствующих участков [7]. Если же участки оцениваются как неперспективные (таких может быть большинство, поскольку необходимые издержки, как правило, оказываются слишком высокими по сравнению с ожидаемыми доходами), их разработка откладывается. Чтобы избавиться от малопривлекательных для инвестиций участков, требующих расходов, корпорация принимает решение выставить их на продажу. Ее руководители полагают, что другие фирмы могут заинтересоваться предложением дешево приобрести права на разработку участков, подходящих им с географической или стратегической точки зрения [5].
Менеджерами компании, выполняющим программу реализации активов, предложено изменить способ расчета стоимости участков. Обычный подход заключается в том, чтобы определить стоимость участка, если начать освоение немедленно. Суть нового метода состоит в оценке самой возможности начать эксплуатацию участка в будущем, если объем извлекаемых запасов золота возрастет в результате внедрения новых технологий добычи. Иными словами, руководство корпорации должно применить к условиям своей отрасли идею, заложенную в опционах.
С помощью простой финансовой модели менеджеры могут определить опционную стоимость участков на пять лет вперед, учитывая неопределенность в отношении запасов золота и будущих цен на него, а также возможность гибкой реакции компании на изменения этих факторов. После переоценки портфеля руководители могут принять решение сохранить те участки, опционная стоимость которых окажется высокой, а остальные выставить на продажу уже не по символической цене, а по соответствующей их истинной стоимости [5].
Общий вид модели Блэка-Шоулза расчета стоимости финансового опциона, используемый далее, следующий:
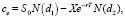 (9)
(9)
где ce – премия европейского опциона колл; S0 – курс спот акции; X – цена исполнения опциона; N(d) – функция нормального распределения; N(d1) – риск-нейтральная вероятность события, что опцион принесёт выигрыш; N(d2) – как вероятность события, что опцион будет исполнен. Модель Блэка-Шоулза-Мертона однозначно отражает влияние ключевых параметров на стоимость опциона (таблица 1).
Таблица 1
Влияние параметров модели Блэка-Шоулза на стоимость опциона (колл)
|
Фактор |
Влияние на цену опциона |
|
Текущая цена базового актива S0 |
прямое |
|
Цена исполнения опциона X |
обратное |
|
Время до истечения опциона t |
прямое |
|
Риск (изменчивость цены) актива |
прямое |
|
Безрисковая ставка |
прямое |
|
Промежуточная доходность актива |
обратное |
Для интерпретации переменных формулы (9) в приложении к реальным проектам необходимо установить, как в контексте решаемой задачи будут преобразованы параметры «традиционной» модели Блэка-Шоулза (таблица 2).
Таблица 2
Соответствие параметров модели Блэка-Шоулза и модели реального опциона
|
Параметр |
Модель Блэка-Шоулза |
Модель реального опциона |
|
S0 |
цена базового актива |
текущая стоимость объекта инвестирования |
|
X |
цена исполнения опциона |
Финансовые обязательства, которые необходимо выполнить, чтобы достичь цель проекта |
|
T |
время до истечения опциона |
период времени, на который отложено решение об инвестировании |
|
R |
безрисковая ставка процента, соответствующая сроку опциона |
безрисковая ставка процента, соответствующая сроку опциона |
|
σ |
дисперсия доходности актива |
степень неопределенности или риска проекта |
В контексте этой статьи дополнительный интерес представляет учет специфичности базового актива в модели реальных опционов.
Понятие специфического актива определяется следующим образом: активы, которые являются результатом специализированной инвестиции, и которые не могут быть перепрофилированы для использования в альтернативных целях или альтернативными пользователями без потери производственного потенциала. Иначе говоря, это активы с низкой альтернативной стоимостью, которые, например, сложно продать или применить в другой области. Примерами специфических активов могут- являться: узкоспециализированное оборудование или автоматизированные производственные комплексы [8].
Специфические активы подразделяют в соответствии с [8]:
– специфичностью местоположения, обуславливающей низкую мобильность активов и с высокие издержки ввода в эксплуатацию;
– специфичностью физических активов, определяемой физическими свойствами (например, печи электростанций обычно рассчитаны на определенный тип угля (с определенной влажностью, содержанием серы, химическим составом);
– специфичностью нематериального актива (человеческого капитала), возникающей вследствие приобретения работником навыков, которые могут быть применены только на этой позиции;
– целевыми активами – результатами инвестиций, направленных на расширение производственных мощностей в целях удовлетворения спроса конкретной группы покупателей.
Таким образом, специфическими могут выступать не только активы, выраженные в виде оборудования или ресурсов, но и в виде знаний и профессиональных навыков специалистов различного профиля, которые работают в определенной области. Например, специфичность нематериальных или физических активов может выражаться, соответственно, в особенностях трудовой деятельности специалистов данного профиля (оператор автоматической линии, технолог высокой квалификации, инженеры на производстве оптических приборов и т.д.) и в уникальности оборудования (доменные печи, бурильное оборудование и т.п.). Для таких отраслей как добывающая промышленность также характерна и специфичность местоположения.
В целях настоящей работы разработана система экспертной оценки специфичности актива (таблица 3).
Для учета вклада в стоимость базового актива его специфичности предлагается модифицировать исходную модель Блэка-Шоулза, используя коэффициент балльной оценки специфичности актива, который интегрирует следующие критерии:
1. если сумма баллов меньше 25 % от всей совокупности, то актив следует считать обычным;
2. если сумма баллов в диапазоне 25 %-75 % от общей суммы, то актив следует считать специфическим;
3. если сумма баллов больше 75 % от общей суммы, то актив следует считать интерспецифическим.
Специфичность актива определяется с использованием балльной оценки, представленной в таблице 3.
Таблица 3
Экспертная балльная оценка специфичности актива
|
Классификационный признак актива |
Балльная оценка |
|
1. Специфичность по месту расположения актива: |
|
|
– перемещаемый |
0 |
|
– стандартизированный неперемещаемый |
1 |
|
– уникальный неперемещаемый |
2 |
|
2. Технологическая специфичность: |
|
|
– стандартная |
0 |
|
– специализированная |
1 |
|
– уникальная |
2 |
|
3. Специфичность человеческого капитала: |
|
|
– неквалифицированный персонал |
0 |
|
– квалифицированный персонал |
1 |
|
– уникальные специалисты в данной сфере деятельности |
2 |
|
4. Защищенность торговой маркой (товарным знаком): |
|
|
– актив не защищен |
0 |
|
– актив защищен |
2 |
|
5. Специфичность инвестиций в производственную инфраструктуру, рассчитанную на потребности определенной группы потребителей: |
|
|
– универсальные объекты инфраструктуры |
0 |
|
– объекты инфраструктуры, специализированные под конкретного потребителя (конкретный продукт), но допускающие возможность переналадки |
1 |
|
– объекты инфраструктуры, специализированные под конкретного потребителя (конкретный продукт), не допускающие возможности переналадки |
2 |
|
6. Специфичность активов во времени: |
|
|
– актив может быть замещен в любое время |
0 |
|
– актив может быть приобретен или замещен только в долгосрочном периоде |
1 |
|
– актив не может быть замещен ни в краткосрочном, ни в долгосрочном периоде |
2 |
|
7. Компенсация ущерба |
|
|
– не будет покрывать ущерб |
0 |
|
– покроет только небольшую часть или четверть от суммы ущерба |
1 |
|
– покроет половину суммы ущерба |
2 |
|
– покроет либо две трети, либо всю сумму ущерба |
3 |
|
8. Доля от финансового результата |
|
|
– получает треть и менее от доходов |
0 |
|
– получает половину всех доходов |
1 |
|
– получает две трети и более от дохода |
2 |
Коэффициент, основанный на экспертной балльной оценке, рассчитывается как:
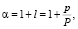 (10)
(10)
где α – индекс специфичности актива (мультипликатор стоимости); l – доля баллов; p – сумма баллов при оценке специфичности активов; P – максимальная сумма баллов (максимальная сумма баллов равна 17).
В виду того, что специфичность актива подразумевает повышенные риски, то необходимо ввести коэффициент, влияющий на волатильность актива. Одним из основных рисков является риск оппортунизма. В балльном методе оценки специфичности активов выделяется три уровня этого риска: высокий уровень, средний уровень и практически отсутствующий. В первых двух случаях рассматриваемые баллы будут иметь отрицательные значения (-2 балла и -1 балл соответственно), так как оппортунизм влечет за собой неминуемые потери и повышение вероятности банкротства, или полного поглощения. Свяжем отсутствие риска с нулевым значением вероятности появления оппортунизма. На основе вышеописанной классификации можно использовать следующий коэффициент волатильности:
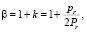 (11)
(11)
где β – коэффициент волатильности актива; k – доля баллов (не должно превышать 0,5); pr – балл при экспертной оценке риска; Pr – максимально возможный балл.
Модифицированная модель Блэка-Шоулза с использованием вышеописанных коэффициентов выглядит следующим образом:
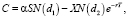 (12)
(12)
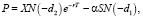 (13)
(13)
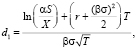 (14)
(14)
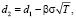 (15)
(15)
где C – цена опциона «call»; P – цена опциона «put»; S – приведенное значение денежных потоков выгод от реализации инвестиционного проекта; α – коэффициент специфичности актива; β – коэффициент волатильности актива; N(x) – кумулятивная функция распределения стандартного нормального распределения; X – приведенное значение потока инвестиций; r – безрисковая процентная ставка; T – время до экспирации опциона; σ – уровень риска проекта.
Рассмотрим модифицированный вариант модели Блэка-Шоулза для реального опциона на отказ [9].
В случае опциона на отказ от проекта в качестве базового актива выступает поток выгод от реализации проекта, а цена исполнения опциона задает либо нижнюю границу убытков, либо экономию от отказа реализации проекта [10] Степень неопределенности представляет собой стандартное отклонение стоимости проекта от средней величины. Также проект имеет ограниченный срок, а, следовательно, приведенная стоимость со временем снизится- сокращается промежуток времени лет, в течение которого будут возникать денежные потоки. Предположим, что эта стоимость пропорциональна времени, оставшегося до срока окончания проекта. Тогда модель Блэка-Шоулза для оценки стоимости опциона на отказ может быть уточнена следующим образом:
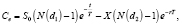 (16)
(16)
где
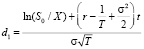 , (17)
, (17)
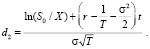 (18)
(18)
Как и в классической модели оценки финансового опциона величину N(d1) можно рассматривать как риск-нейтральную вероятность, что опцион принесёт выигрыш, а N(d2) – вероятность его исполнения.
Для оценки эффекта от применения коэффициентов рассчитаем стоимость опциона «call» на основе модели (16) и ее модификации (12) с учетом специфичности базового актива. Параметры классической и модифицированной моделей будем рассматривать с позиции реальных опционов. Рассмотрим пример некоторого инвестиционного проекта, для которого существует опцион «call», параметры которого принимают следующие значения (табл. 4) [11].
Таблица 4
Параметры реального опциона
|
Параметр |
Значение |
|
Текущая стоимость актива, S0 |
750 000 руб. |
|
Остаточный срок, T |
5,5 лет |
|
Цена исполнения опциона, X |
675 000 руб. |
|
Процентная ставка, r |
10 % |
|
Степень риска, σ |
23 % |
Таблица 5
Экспертная оценка актива
|
Классификационный признак актива |
Балльная оценка |
|
1. Специфичность по месту расположения актива: Перемещаемый |
0 |
|
2. Технологическая специфичность: Специализированная технология |
1 |
|
3. Специфичность человеческого капитала: Уникальные специалисты в данной сфере деятельности |
2 |
|
4. Защищенность торговой маркой: Актив защищен |
2 |
|
5. Специфичность инвестиций в производственную инфраструктуру, рассчитанную на потребности определенной группы потребителей: Объекты инфраструктуры, специализированные под конкретного потребителя (конкретный продукт), но допускающие возможность переналадки |
1 |
|
6. Специфичность активов во времени: Может быть приобретен или замещен только в долгосрочном периоде |
1 |
|
7. Компенсация ущерба: Покрытие только небольшой части или четверти от суммы ущерба |
1 |
|
8. Доля от финансового результата: Получение трети и менее от доходов |
0 |
|
Итого баллов |
8 |
В качестве базового актива выступает актив, который был оценен экспертом по критериям, приведенным в таблице 3. В результате была получена экспертная оценка, приведенная в табл. 5.
Так как оценка составляет 47 % от общего количества баллов, то данный актив является специфическим. Далее экспертом оценен риск оппортунизма со стороны контрагента на основе его репутации. В результате анализа деятельности контрагента был сделан вывод о среднем уровне риска оппортунизма.
На основе полученной оценки были рассчитаны коэффициенты α и β для модифицированной модели Блэка-Шоулза:
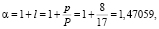 (19)
(19)
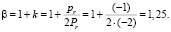 (20)
(20)
По значениям этих коэффициентам однозначно определяются параметры модели:
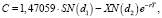 (21)
(21)
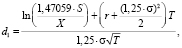 (22)
(22)
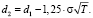 (23)
(23)
Далее рассчитаем стоимость опциона «call», используя классическую и модифицированную модели Блэка-Шоулза. Результаты вычислений параметров и стоимости представлены в табл. 6.
Таблица 6
Результаты вычислений
|
Показатели |
Классическая модель |
Модифицированная модель |
|
d1 |
1,48468 |
1,88110 |
|
d2 |
0,94529 |
1,20686 |
|
N(d1) |
0,93119 |
0,97002 |
|
N(d2) |
0,82774 |
0,88626 |
|
C |
376 032,27 руб. |
724 732,85 руб. |
Стоимость опциона «call» по классической модели Блэка-Шоулза составила 376 032,27 руб., а по модифицированной – 724 732,85 руб. Эффект от модификации составил 93 %, то есть учет уровня специфичности актива повысил стоимость опциона на 348 700,58 руб.

