Введение
Контакт-центр или колл-центр (call center) представляет собой централизованный офис, предоставляющий услуги населению, который используется при организации работы компаний, работающих в сфере транспортных услуг, связи, продаж и т. п. В современном мире контакт-центры играют важную роль. Известно из [1], что все крупные мировые компании имеют по крайней мере один контакт-центр для обслуживания своих клиентов.
Как известно [2], большая часть операционных затрат таких центров составляет заработная плата операторов. В связи с этим одной из ключевых задач планирования и организации работы контакт-центров является оценка оптимальной численности обслуживающих операторов. Решение этой задачи невозможно без разработки, анализа и исследования математической модели современного контакт-центра, а также без нахождения и оценки ее основных вероятностных характеристик.
В моделировании работы контакт-центров широко применяются методы теории массового обслуживания. Наиболее простой моделью контакт-центра является система массового обслуживания M/M/N. Ее называют C-система Эрланга. В этой модели предполагается, что процесс поступления звонков является пуассоновским, а времена обслуживания звонков клиентов имеют экспоненциальное распределение. Эта модель не учитывает отказы в обслуживании и нетерпеливость клиентов. Другой известной и достаточно простой моделью является система M/M/N/0. Ее принято называть B-система Эрланга без буфера. В работе [3] исследована система обслуживания M/M/N/R-N c конечным буфером и нетерпеливыми запросами. Ее называют A-система Эрланга. В работе [4] определены характеристики производительности для такой системы найдены характеристики с произвольным распределением времен нетерпеливости запросов. В работе [5] исследована зависимость характеристик A-система Эрланга от ее параметров, в [6] рассмотрена возможность совершения запросами повторных попыток попасть на обслуживание, а в работе [7] рассмотрена система обслуживания с двумя типами запросов с уходом и без ухода из-за нетерпеливости. В [8] показана двухуровневая модель контакт-центра, которая учитывает возможность того, что оператор в случае невозможности обслужить запрос, переводит клиента на второй уровень, где его будет обслуживать другой более компетентный оператор. Обзор литературы по моделированию работы контакт-центров приведен в работах [2, 9].
Анализ существующих математических моделей показывает, что классический подход при их разработке не учитывает некоторые важные технологические процессы, которые имеют место в современных контакт-центрах. Например, очень важными являются: наличие предварительного многоуровневого голосового обслуживания (IVR–Interactive Voice Response) и досрочное покидание системы нетерпимыми клиентами в период ожидания ответа оператора.
Целью данной работы является построение обобщенной математической модели контакт-центра, учитывающей влияние перечисленных выше факторов, ее исследование и анализ, а также нахождение и оценка основных вероятностных характеристик. Эта постановка в большей степени согласуется с реалиями функционирования контакт-центров, хотя и приводит к достаточно сложной математической модели.
Математическое описание модели
Структура основных элементов разрабатываемой модели контакт-центра изображены на рисунке.
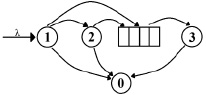
Модель работы контакт центра
Будем полагать, что поступление запросов в систему образуют пуассоновский процесс, т. е. процесс прибытия происходит по Пуассону с интенсивностью независимой от времени.
Запросы клиентов для получения разного рода информационных услуг, поступившие в контакт-центр, далее обслуживаются устройствами IVR или операторами. Обслуживание клиента может включать в себя четыре стадии: двухуровневое обслуживание с помощью IVR, нахождение в очереди к оператору и обслуживание оператором:
τ = τ1 + τ2 + τ3 + τ4,
где τi – независимые и экспоненциально распределенные случайные величины с параметрами μi, которые характеризуют длительность этапа обслуживания.
С помощью IVR клиент может самостоятельно получить необходимую информацию. IVR система предварительно записанных голосовых сообщений, которая выполняет функцию перенаправления звонков внутри контакт-центра с помощью вводимой клиентом на клавиатуре телефона информации. На каждом этапе IVR воспроизводится голосовое меню или аудиосообщение. Будем полагать, что продолжительность таких сообщений в среднем одинакова, а значит параметры μ1 = μ2. Обслуживание каждого нового запроса начинается на первой фазе. Звонок клиента после первой фазы с вероятностью pi переходит к обслуживанию на (i + 1) фазу, а с вероятностью qi переходит на третью фазу в очередь. А получив необходимою информацию, клиент с вероятностью (1 – pi – qi) завершает обслуживание и покидает систему. Известно из [2], что около 65 % клиентов контакт-центров фактически завершают свое обслуживание через IVR. Остальные 35 % выражают необходимость поговорить с оператором.
Если есть свободный оператор, клиента немедленно соединяют с ним для обслуживания. В противном случае запрос клиента присоединяется к очереди, при этом ему могут сообщать его номер в очереди и ориентировочное время ожидания. Будем предполагать, что длительность нахождения каждой заявки в очереди распределена по экспоненциальному закону с параметром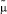 
, характеризующим время ожидания в очереди. В зависимости от его номера в очереди клиент принимает решение, ожидать или уйти из системы досрочно без обслуживания из-за нетерпеливости. Заявка переходит из очереди на третью фазу с вероятностью s или с вероятность (1 – s) покидает очередь и систему, не дождавшись ответа оператора. Обслуживание клиента всегда завершается после третьей фазы, т. е. после общения с оператором контакт-центра.
Считаем, что от обслуживания каждого абонента система получает прибыль, в то время как содержание оператора требует затрат. Необходимо определить такое число операторов, при котором прибыль центра была бы максимальной. Проведем исследование процесса изменения числа обслуживаемых запросов клиентов на каждом этапе, применяя подход, описанный в [10].
Исследование процесса изменения числа обслуживаемых запросов
Состояние системы массового обслуживания в произвольный момент времени t определяется вектором:
n(t) = {n1(t), n2(t), n3(t), m(t)}T,
где ni(t) – число клиентов, обслуживаемых на i-й фазе в момент t, а m(t) – число клиентов в очереди к оператору. Случайный процесс n(t) является четырехмерной цепью Маркова с непрерывным временем. Определим распределение вероятностей
P(n1, n2, n3, m, t) = = P{n1(t) = n1, n2(t) = n2, n3(t) = n3, m(t) = m}
и найдем первые и вторые моменты числа обслуживаемых запросов клиентов на каждом этапе. Данный подход применялся в работах [11, 12, 13].
По формуле полной вероятности запишем систему дифференциальных уравнений
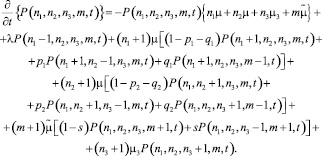
Обозначим характеристическую функцию числа запросов клиентов в такой системе в произвольный момент времени t в виде:
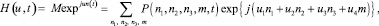
где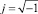 
– мнимая единица.
Учитывая, что
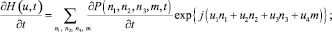
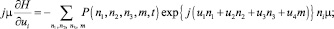
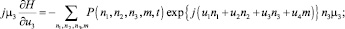
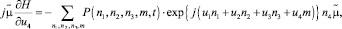
из системы дифференциальных уравнений Колмогорова для распределения вероятностей P(n1, n2, n3, m, t) запишем систему для функции H(u, t):
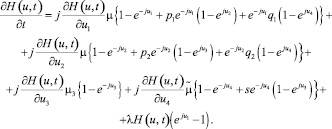
В явном виде не представляется возможным записать характеристическую функцию H(u, t), поэтому для нахождения вероятностных характеристик математической модели применим метод моментов, изложенный подробно в [14, 15].
Нахождение вероятностных характеристик числа обслуживаемых запросов
Согласно методу моментов для нахождения моментов первого порядка найдем производные 1-го порядка в нуле от характеристической функции. Для этого необходимо подставить в дифференциальное уравнение его решение и продифференцировать полученное тождество поочередно по u1, u2, u3, u4. Обозначив
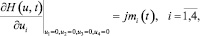
получим следующую систему четырех обыкновенных дифференциальных уравнений, определяющих mi(t):
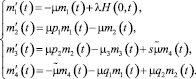
Из начального условия H(0, t) = 1, запишем:
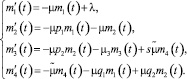(1)
Поскольку первый начальный момент является математическим ожиданием, то функции mi(t) – определяет среднее число запросов клиентов, находящихся на обслуживании на первой, второй, третьей фазе и в очереди перед третьей фазой в произвольный момент t. Система (1) является линейной системой дифференциальных уравнений с постоянными коэффициентами. Решение данной системы не представляет затруднений, если разбить ее на две подсистемы и решать отдельно.
Учитывая, что в начальный момент времени в системе на всех этапах отсутствуют запросы клиентов, получим решение системы (1). Найдено, что среднее число запросов клиентов, находящихся на первом этапе, может выть вычислено по формуле
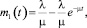
на втором этапе по формуле
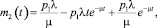
среднее число запросов третьей фазы рассчитывается по формуле
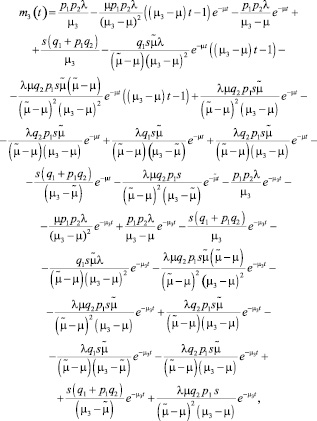
в буфере по формуле
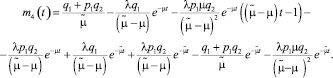
Таким образом, были найдены решения четырех дифференциальных уравнений системы, определяющие средние вероятностные характеристики числа обслуживаемых запросов клиентов на каждой фазе (первые моменты). Аналогичным методом могут быть найдены вторые моменты.
Заключение
В данной статье исследуется система массового обслуживания с многофазным обслуживаем запросов с многоуровневым IVR и нетерпеливыми запросами, которая может использоваться для моделирования и оптимизации функционирования контакт-центра. В данной модели предполагается, что входной поток запросов является стационарным, который не учитывает изменение интенсивности потока звонков во времени. Предложенная математическая модель процесса обработки вызовов в виде четырехфазной системы массового обслуживания, позволяет оптимизировать деятельность контакт-центра. Задача данной модели состоит в обработке максимального количества заявок с помощью автоинформатора (IVR), тем самым уменьшится число клиентов, переходящих на последний уровень (общение с оператором). Такая модель позволит ускорить процесс обслуживания клиентов и оптимизировать расходы.