Научный журнал

Вестник Алтайской академии экономики и права

Print ISSN 1818-4057

Online ISSN 2226-3977

Перечень ВАК

Введение

Уровень успеваемости студента в ВУЗе является своеобразной формой диагностики и прогнозирования степени отдачи будущего специалиста. В свою очередь успехи студентов – это показатель деятельности ВУЗа в решении учебно-воспитательных задач. Для того, чтобы решать данные задачи максимально эффективно требуется постоянная объективная оценка, корректировка и управление. Однако, без прогнозирования управление невозможно. Поэтому возникает необходимость прогнозирования посещаемости, и, как следствие, успеваемости студентов на всех этапах обучения [6].

Целью данного исследования является разработка прогнозных моделей для оценки успеваемости и посещаемости занятий студентами, возможности их отчисления из ВУЗа.

Наличие таких моделей позволит уделять более пристальное внимание студентам, которые попадают в группу риска большого количества долгов по учебным дисциплинам, а как следствие, будут претендентами на отчисления. Определение таких студентов на ранних этапах позволит более детально и персонально работать с ними для того, чтобы они более успешно справлялись с учебной нагрузкой [6].

Выбытие студентов – явление значимое и для вуза в силу его экономических интересов, и для общества в целом, поскольку порождает социальные проблемы, такие как нехватка квалифицированных специалистов. Например, в США уровень отчислений является одним из важнейших показателей конкурентоспособности вуза и отражает, с одной стороны, привлекательность вуза (его способность удержать студентов, предотвратить их переход в другой вуз), а с другой – эффективность образовательной политики университета в адаптации студентов к обучению, помощи им в учебном процессе. И если в зарубежных вузах сложилась традиция исследования выбытия из университетов студентов, то в России вопросу отсева студентов из вузов до сих пор уделялось мало внимания [3].

Материалы и методы исследования

В данной работе речь пойдет о создании прогнозных моделей успеваемости студентов по текущим оценкам с помощью технологий анализа данных. Методы прикладной статистики являются надежным математическим инструментом, позволяющим обрабатывать и анализировать собранные статистические данные. Для проведения исследования был использован ППП Statistica, в качестве инструментальных методов регрессионный анализ, модели бинарного выбора, кластерный анализ.

Основным информационным источником для проведения исследования стали данные проведенного анкетирования среди студентов экономического, физико-математического и электроэнергетического факультетов (студенты 38 академических групп), также данные по отчисленным студентам, представленным деканатами ЭФ и ФМФ Института цифровых технологий Марийского государственного университета [1].

В работе представлена методика построения прогнозных оценок студентов института цифровых технологий Марийского государственного университета, выполненная на основании данных электронной системы «Студент» и проведенного анкетирования 290 студентов по 12 параметрам, охватывающим показатели, характеризующие умение учиться (результаты ЕГЭ, средний балл по аттестату), подготовленность к самостоятельной жизни (проживание в общежитии) и желание и умение учиться (текущая посещаемость и успеваемость) и др. [1].

Результаты исследования и их обсуждение

В рамках исследования были рассмотрены три модели.

В первой, в качестве зависимой переменной выступает показатель «Количество долгов», во второй – показатель «Количество пропусков», в третьей – показатель «Количество отчислений». Для каждой из моделей были построены регрессионные статистические модели, классификации и кластеризации, вероятностные модели дискриминантного и логит-анализа.

Таблица 1

Матрица парных корреляций

Для определения набора независимых переменных, влияющих на количество долгов и пропуски студентов была построена корреляционная матрица.

Анализируя значения коэффициентов корреляции можно сделать вывод, что наибольшее влияние на «Количество долгов» студента оказывают такие переменные как «Пол», «Территориальное происхождение», «Количество пропусков», «Средний балл зачетной книжки» и «Средний балл по аттестату». При этом, чем выше «Средний балл зачетной книжки» и «Средний балл по аттестату», тем меньше количество долгов.

Что касается «Количества пропусков» студента, то здесь наибольшее влияние оказывают «Возраст», «Количество долгов», «Результаты ЕГЭ» и «Средний балл по аттестату». При увеличении «Количества долгов», «Количество пропусков» увеличивается, а при увеличении других переменных – уменьшается.

Анализ показателя: «Количество долгов»

Для исследования связи между результатами успеваемости студентов – переменная «Количество долгов» -Y и массивом данных, включающих обезличенную информацию о студентах (табл.1) были построены регрессионные модели в пакете Statistica:

Модель с включением всех переменных имеет вид:

R2 = ,19387646, F (7,231) = 7,9367, p < 0,00000, SE = 0,39839.

По значениям стандартизованных коэффициентов β видно, что наиболее значимыми переменными, влияющими на Количество долгов, т.е. успеваемость студентов оказывают показатели: Территориальное происхождение (откуда приехали студенты – городские, сельские или из других городов (чаще иностранцы), Количество пропусков и Средний балл зачётной книжки. Причем, сем выше средний балл по аттестату у студента, тем меньше у него долгов (привык учиться).

В данном уравнении не все переменные по критерию Стъюдента являются значимыми, окончательная модель имеет вид:

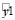= 0,84 + 0,22 Территориальное происхождение + 0,004 Количество пропусков – – 0,24 Средний балл по аттестату

где 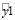– Количество долгов.

Уравнение статистически значимо.

R2 = 0,16, F (3,235) = 15,52,

p<0,00000, SE=0,40

Коэффициенты уравнения показывают, что чем больше количество пропусков, тем больше у студентов долгов, чем выше средний балл по аттестату (хорошо учился в школе), тем долгов у студента меньше. В данную модель не вошла переменная – средний балл ЕГЭ, т.к. видимо при сдаче ЕГЭ школьники показывают определенные знания, а не уровень своей подготовки за время учебы в школе.

Анализ показателя: «Средний балл зачетной книжки»

Анализ показателя: «Средний балл зачетной книжки» в основном зависит отСреднего балла по аттестату и, в меньшей степени от среднего балла ЕГЭ:

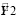= 0,85 + 0,004 Результаты ЕГЭ +

+ 0,55 Средний балл по аттестату

R2 = 0, 35, F (2,236) = 62,87,

p<0,00000, SE=0,40,

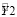– Средний балл зачетной книжки.

Анализ показателя: «Количество пропусков»

Для определения зависимости количества пропусков от переменныхY2 и массивом данных, включающих обезличенную информацию о студентах (табл.1) были построены регрессионные модели в пакете Statistica:

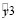= 72,42 – 2,5 Курс + 7,62 Общежитие + +6,4 Количество долгов + 6,07 Средний балл зачетной книжки – 0,09 Результаты ЕГЭ – – 15,8 Средний балл по аттестату

R2 = 0,28, F(6,232) = 14,79,

p < 0,00000,SE = 14,82.

По стандартизованным коэффициентам β, можно сделать вывод, что на количество пропусков большее влияние оказывает переменная – «Средний балл по аттестату», причем, чем выше балл у студента был в школе (ответственность за обучение), тем меньше пропусков у данного студента (β = -0,38). Студенты, проживающие в общежитии, имеют большее количество пропусков (отсутствует самодисциплина).

Анализ показателя: «Отчисления студентов»

Для определения причин и возможностей отчисления студентов были построены две вероятностные модели. Инструментами для решения выбраны методы логистической регрессии и дискриминантного анализа (методы машинного обучения). Таким образом, была создана новая база данных, состоящая из студентов ЭФ и ФМФ включающая облачающихся на данный момент студентов и отчисленных по результатам осенней сессии. База составила 160 записей.

Анализ (прогноз) отчислений студентов. Решение с использованием логистической регрессии

Логит-модель – это эконометрическая модель, которая относится к классу моделей, для которых традиционные методы регрессионного анализа не подходят. Ее основное отличие заключается в том, что зависимая переменная может принимать только ограниченное количество значений, обычно 0 или 1. Основная цель анализа заключается в оценке вероятности того, что зависимая переменная примет одно из этих значений. Для решения этой задачи используется логистическая функция, представленная в логарифмической форме [8]. В данной модели в качестве зависимой переменной Y приняты следующие обозначения:

1 – студент отчислен,

0 – студент учится.

В качестве независимых переменных также использованы данные:

Форма финансирования, Курс, Пол, Возраст, Территориальное происхождение, Общежитие, Количество пропусков, Количество долгов, Средний балл зачётной книжки, Результаты ЕГЭ – используемые при анкетировании (табл. 2).

Теперь рассмотрим р-уровень гипотезы. В нашем случае р-уровень ниже 5% (р=0,00000). Значение статистики χ2-квадрат для разницы между текущей моделью и моделью, содержащей лишь свободный член, высоко значимо (χ2 = 166,1128). Поэтому можно сделать вывод, что вошедшие в модель переменные влияют на принятие решения об отчислении студента. Для построения бинарной логистической модели использовался многошаговый регрессионный анализ, основанный на исключении из модели несущественных факторов по тесту Вальда, которая показала значимость только четырех коэффициентов (рис. 1) при переменной Количество пропусков, Количество долгов, Средний балл зачетной книжки и результаты ЕГЭ. Задавая различные методы оценивания параметров, был выбран метод оценивания: Метод оценивания Розенброка и Квази-Нъютоновский.

Таблица 2

Статистические характеристики полученной модели – результаты логит-регрессии

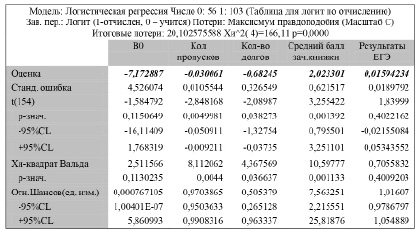
Рис. 1. Результаты решения

Модель бинарного выбора имеет вид:

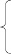Y = (1 + e-z)-1

z = –7,17 – 0,03*Кол. пропусков – 0,68*Кол. долгов +2,02*Средний балл зач. книжки + 0,016*Результаты ЕГЭ

Для оценки качества моде6ли используют аналог R2 линейной регрессии McFadden. Индекс McFaddenR2 называют индексом отношения правдоподобия.

R2 = 1 – ,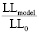

где – логарифм функции правдоподобия – (Likelihood): forthismodel = 40,25, а LL0 –логарифм функции правдоподобия модели только с константой =interceptonly: 206,31. Очевидно, что LL0>LLmodel. Чем больше различаются их значения, тем лучше модель.

McFaddenR2 = 0,83 или 83%. Т.е. на 83% выбранные показатели оказывают влияние на принятие решение об отчислении студента.

LRstatistic (-2 *(l – 1)) – тест отношения правдоподобия является аналогом F –статистики в линейных регрессионных моделях. Используется для проверки значимости модели. χ2 = 166,11.

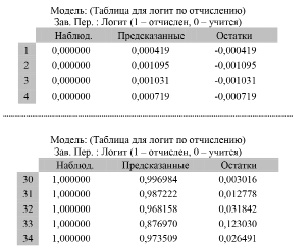
Рис. 2. Наблюдаемые, предсказанные и значения остатков

Логит-модель гарантирует, что предсказанные значения всегда будут находиться внутри отрезка [0,1]. Поэтому можем рассматривать полученные значения как вероятности (рис. 2).

Например, по рисунку 2 можно увидеть, что предсказанная вероятность того, что третий студент не будет отчислен, подтверждается вероятностью равной 0,001031, что и соответствует исходным данным. Мы видим, что действительно третий респондент будет учиться.

Для студента под номером 30, 31, 32, 33 и 34 вероятность отчисления близка к 1, что и соответствует исходным данным, данные студенты были отчислены (по данным деканата).Построенная модель бинарного выбора позволяет прогнозировать возможность отчисления любого студента. Подставляя конкретные данные в модель можно получить прогнозную оценку студента.

ПРИМЕР 1.

Проверим студента под номером 3 в базе данных -01.03.01 Математика (Математические и инструментальные методы в экономике), группа ММ-11 к какой категории (отчислен или учится) будет отнесен наш студен, согласно построенной модели. По данным деканата ЭФ данный студент отчислен. Подставим значения его параметров в модель:

Согласно модели бинарного выбора, мы подставляем в модель вместо переменных конкретные значения студента из базы данных:

Количество пропусков – 366 часов;

Количество долгов – 8;

Средний балл зачетной книжки – 2,2;

Результаты ЕГЭ – 154.

Модель будет иметь вид:

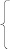Y = (1 + e-z)-1

z = -7,17 – 0,03*366 – 0,68*8 +2,02*2,2 + 0,016*154

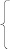Z= -16,682;

Y = 1/(1 + exp-(-16,682)) = 0,9999999943,

т.е. его вероятность равна 1 – студент должен быть отчисленным, что соответствует записи деканата.

ПРИМЕР 2

Проверим другого студента под номером 30 в базе данных 01.03.01 Математика (Математические и инструментальные методы в экономике), группа ММ-11 к какой категории (отчислен или учится) будет отнесен наш студен, согласно построенной модели. Подставим значения его параметров в модель:

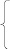Y = (1 + e-z)-1

z = -7,17 – 0,03*2 – 0,68*0 + 2,02*4,5 + 0,016*221

Z=6,33;

Y = Y= 1/(1+exp6,33))= 0,001779,

т.е. его вероятность равна 0 –студент учится (не отчислен).

Таблица 3

Корректно классифицированные наблюдения

Оценить качество построенной модели можно также, используя параметр Отношение несогласия. В таблице 3 отображены наблюдения, которые были правильно и неправильно классифицированы в соответствии с полученной моделью.

Из данной таблицы видно, что модель правильно прогнозирует ответ для 101 из 103 опрошенных респондентов (98% правильных ответов). Модель также правильно предсказала отчисление студентов для 52 из 56 опрошенных (92,85% правильных ответов). Элементы, расположенные вне главной диагонали, показывают количество неверно классифицированных студентов. В нашем случае таких оказалось 6. Всего были правильно классифицированы 153 из 159 студентов, т.е. 96,23%.Подводя итоги, можно сказать, что построенная модель адекватна исходному процессу и с известной долей уверенности с ее помощью можем определять целевую аудиторию студентов.

Анализ (прогноз) отчислений студентов. Решение с использованием дискриминантного анализа

Для проведения дискриминантного анализа использовались данные по 159 студентам по экономическому и физико-математическому факультету. В качестве независимых переменных также использованы данные: Форма финансирования, Курс, Пол, Возраст, Территориальное происхождение, Общежитие, Количество пропусков, Количество долгов, Средний балл зачётной книжки, Результаты ЕГЭ- используемые при анкетировании. Группирование данных проводилось по переменной группа, которой присваивалось два значения:

группа G_1:0 – студент учится,

группа G_2:1 – студент отчислен

По таблице исходных данных в пакете Statistica была построена матрица классификации, которая показала процент правильно и неправильно отнесенных наблюдений к своим группам (табл. 4).

Таблица 4

Матрица классификации

Таблица 5

Итоги анализа дискриминантной функции

Лямбда Уилкса: 0,23078, прибл. F (10,148) = 49,331 p < 0,0000 показатели качества модели.

По данной матрице видно, что по студентам, которые учатся, все были правильно отнесены к данной группе. По отчисленным студентам 7 человек из 56 неверно отнесены к данной группе. Это объясняется тем, что не все студенты, были отчислены по неуспеваемости. Есть студенты, которые перешли в другой вуз, или факультет. Итоги анализа дискриминации отражены в таблице 5.

Такие показатели, как Курс, Пол, Возраст, Территориальное происхождение, Общежитие и Результаты ЕГЭ не имеют больших различий при разделении студентов на группы. Наиболее значимыми при разбиении на группы являются показатели: Форма финансирования, Количество пропусков, Количество долгов, Средний балл зачетной книжки.Для возможности отнесения новых студентов к группам: студент учится или студент может быть отчислен, были построены Функции классификации (табл. 6).

Таблица 6

Функции классификации

Функции классификации в виде уравнений:

S1 (G_1:0) =57.991* Форма финансирования – 4.363* Курс + 4.642* Пол – – 0.061* Возраст + 5.046* Территориальное происхождение + 1.446* Общежитие – – 0.012* Количество пропусков + 0.697* Количество долгов + + 5.035* Средний балл зачётной книжки + 0.269* Результаты ЕГЭ – 68.255;

S2 (G_2:1) = 68,881* Форма финансирования – 5,226* Курс + 4.104* Пол – – 0.079* Возраст + 6,196* Территориальное происхождение + 0,019* Общежитие + + 0.012* Количество пропусков + 1,315* Количество долгов + + 1,430* Средний балл зачётной книжки + 0.266* Результаты ЕГЭ – 70,781;

Программа настроена, по ней можно обучаться, т.е. любых студентов по таким же показателям можно сразу отнести к одной из групп.Для этого значения студента по показателям подставить в оба уравнения. В каком уравнении сумма будет максимальной, к той группе и будет отнесен студент.

ПРИМЕР 1

В качестве примера выберем любого студента из базы данных, например, студент под номером 7 (табл. 7).

Таблица 7

Информация по студенту №7 (из базы данных)

Подставим значения данного студента в уравнения функций классификации:

S1 (G_1:0) =57.991* 1 – 4.363* 2 + 4.642* 1 – 0.061* 22 + 5.046* 3 + 1.446* 1 – – 0.012* 224 + 0.697* 10 + 5.035* 2,7 + 0.269* 179 – 68.255 = 66,864;

S2 (G_2:1) = 68,881*1 – 5,226* 2 + 4.104* 1 – 0.079* 22 + 6,196* 3 + 0,019* 1+ + 0.012* 224 + 1,315* 10 + 1,430* 2,7 + 0.266* 179 – 70,781= 75,991;

Т.к. сумма по группе 2 (75,99139)> суммы по группе 1 (66,86418) студент должен быть отнесен к группе 2 -отчисленных студентов. Студент под №7 по данным деканата отчислен (Абдувахабов Жахонгир Вохиджон угли).

ПРИМЕР 2

В качестве примера выберем любого студента из базы данных, например, студент под номером 30 (табл. 8).

Подставим значения данного студента в уравнения функций классификации:

S1 (G_1:0) =57.991*1 – 4.363* 1 + 4.642* 0 – 0.061* 18 + 5.046* 1 + 1.446* 1 – – 0.012* 2 + 0.697* 0 + 5.035* 5 + 0.269* 183 – 68.255 = 65,156;

S2 (G_2:1) = 68,881*1 – 5,226* 1 + 4.104* 0 – 0.079* 18 + 6,196* 1 + 0,019* 1+ + 0.012* 2 + 1,315* 0 + 1,430* 5 + 0.266* 183 – 70,781 = 53,494;

Таблица 8

Информация по студенту №30 (из базы данных)

Таблица 9

Дискриминантный анализ средние значения по группам группа G_1:0 – студент учится, группа G_2:1 – студент отчислен

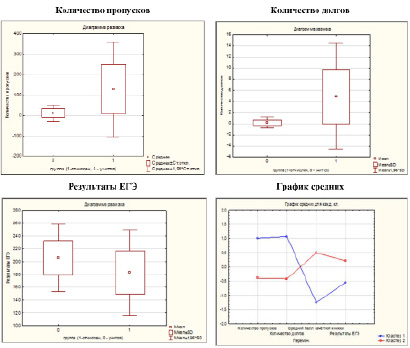
Рис. 3. Классификация студентов по основным показателям: количество пропусков, количество долгов, средний балл зачетной книжки и результаты ЕГЭ Источник: построено авторами с использованием программы Statistica 7.0

Т.к. сумма по группе 1 (65,15631> суммы по группе 2 (53,494) студент должен быть отнесен к группе студентов 1, которые учатся. Студент под №30 по данным деканата – учиться.

Проведенная классификация студентов на две группы методом кластерного анализ, метод итераций – k-средних, наглядно подтвердил разницу между студентами, которые учатся и теми, кто отчислен, или может быть отчислен (рис. 3). Средние значения по группам представлены в таблице 9 и на рисунке 3.

Графическое представление средних значений по показателям двух групп (рис. 3).

Заключение

Предложенные прогнозные модели с использованием машинного обучения помогут своевременно оценить работу любого студента в вузе и своевременно принять меры уже после первой сессии. Более того, основываясь на построенных моделях возможна корректировка учебных планов и планов набора абитуриентов для повышения показателей успеваемости студентов.