Научный журнал

Вестник Алтайской академии экономики и права

Print ISSN 1818-4057

Online ISSN 2226-3977

Перечень ВАК

Введение

В условиях жесткой конкуренции и быстрого изменения внешней среды инвестиционные проекты становятся ключевым механизмом для достижения устойчивого развития и роста компаний. Их успешная реализация напрямую влияет на конкурентоспособность и финансовую стабильность строительных организаций, что подчеркивает актуальность исследований в данной области.

Одним из основных инструментов оценки эффективности инвестиционных проектов является метод определения чистой приведенной стоимости (NPV). Этот показатель позволяет не только оценить экономическую выгоду от реализации проекта, но и сравнить различные альтернативные варианты, что является важным шагом в процессе принятия инвестиционных решений.

В рамках исследования будет проведено сравнение двух альтернатив реализации проекта – «Эконом» и «Комфорт» – с целью выявления оптимальных значений ключевых показателей, включая эффективную ставку, свободный денежный поток строительной организации (FCFF), NPV и чистую прибыль. Для этого будет использована «Мета-модель», разработанная авторами, которая позволит провести комплексный анализ и принять обоснованные инвестиционные решения с учётом всех значимых факторов. Таким образом, данное исследование направлено на углубление знаний в области оценки инвестиционных проектов и совершенствование методов принятия решений в условиях неопределённости.

Материалы и методы исследования

Цель исследования – разработка и внедрение метода оценки инвестиционных проектов экономико-математических методов.

Основными инструментами в процессе исследования выступили: экономико-математические методы: использовались для определения оптимальных параметров модели, включая размеры инвестиционных расходов и доходной части проекта. Имитационное моделирование – применялось для достижения максимальной прибыли и минимизации срока окупаемости инвестиций в условиях неопределенности. Метод обобщенного понижающего градиента использовался для оптимизации целевой функции NPV, что позволило сравнить различные варианты реализации проекта и выбрать наиболее выгодный.

Использованы материалы научных работ, представленных в электронном формате и опубликованные в общедоступной сети «Интернет».

Результаты исследования и их обсуждение

В рамках оценки инвестиционного проекта экономико-математическими методами решение сводится к поиску оптимальных значений переменных, при которых достигается максимальный положительный эффект. Под положительным эффектом понимается чистая прибыль и чистый денежный поток, а также соблюдение параметров LLCR.

Таблица 1

Сравнительный анализ основных экономико-математических методов и моделей оценки инвестиционной проектов

В целях изучения возможности применения различных методов и моделей экономико-математического моделирования для инвестиционного проекта, была проведена оценка существующих моделей. Результат анализ представлен в таблице 1.

В целом, сочетание метода NPV и нелинейного программирования может обеспечить более точную и подробную оценку инвестиционных проектов в недвижимости, особенно при строительстве жилых комплексов, учитывая их сложность, долгосрочность и множество зависимостей между переменными [1, 2, 4, 5, 8].

Для оценки инвестиционного проекта с использованием метода нелинейного программирования, сначала необходимо сформулировать задачу оптимизации. В данном случае, задача заключается в максимизации чистой прибыли от продажи квартир, учитывая переменные затрат и доходов.

Целевая функция для максимизации NPV с использованием метода обобщенного понижающего градиента (GRG) будет представлена в виде формулы NPV, зависящей от переменных проекта. В общем виде, NPV можно представить следующим образом:

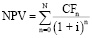
где CFn – денежный поток в периоде;

N – общее количество периодов реализации проекта.

Во вторую очередь необходимо определить переменные, которые будут использоваться для решения целевой функции задачи.

K – класс жилья. Для оценки проекта необходимо определить оптимальный для данной локации класс жилья: эконом, комфорт, бизнес (таблица 2).

SK – суммарная продаваемая площадь проекта, выраженная в квадратных метрах (таблица 2).

CK – общая себестоимость реализации проекта. Переменная будет принимать вид при различном классе жилья (таблица 3).

PK – средневзвешенная цена реализации квадратного метра по проекту. Переменная будет принимать вид при различном классе жилья. Разбивка представлена в таблице 3.

TK – темп реализации жилья, в квадратных метрах. Для расчета темпов продажи жилья были проанализированы среднемесячные продажи в локации – Калининском и Курчатовским районах Челябинской области. Так как при различных классах жилья объем потенциального спроса различен, были применены коэффициенты корректировки, при этом комфорт-класс является базовым значением. Результаты представлены в таблице 4. При этом, для коммерческий площадей используется аналогичное значение.

Таблица 2

Переменная SK при различном варианте класса жилого комплекса

Таблица 3

Переменная PK при различном варианте класса жилого комплекса

Таблица 4

Переменная TK при различном варианте класса жилого комплекса

RPT – процентные платежи по проектному финансированию, необходимые для строительства жилого комплекса, в пересчете на квадратных метр. На текущий момент ставка по проектному финансированию зависит от наполняемости эскроу-счетов банков. Значит, что при различных темпах продаж эффективная процентная ставка будет изменяться. Базовым значением является ставка в 7%.

Таким образом, задача состоит в максимизации F, при заданных переменных.

Первым ограничением выступает переменная TK. Для различных классов в модели используются различные пороговые значения.

Следующим ограничением выступает переменная СС, которая представляет из себя значение расходов на маркетинг и продвижение, в пересчете на один продаваемый квадратный метр. Оптимальным вариантом является диапазон 1-5%.

Третьим ограничением функции выступает ставка проектного финансирования (RPT). В рамках данного кредитного инструмента ставка рассчитывается исходя из наполнения эскроу-счетов банка. Ограничение приведено, в виде обобщающей функции. Финансовая служба строительной организации, осуществляющая согласование кредитных инструментов с банками, были получены значения:

а) минимальная ставка – 3%, при максимальном наполнении эскроу-счетов;

б) максимальная ставка – 9%, при минимальном наполнении эскроу-счетов;

в) базовая ставка – 7%, исходная переменная, которая будет являются вводной для уравнения при методе обобщающего понижающего градиента.

Четвертым ограничением функции выступает переменная SK. Введение данного ограничения необходимо, так как при использовании программного продукта Excel для решения уравнения, переменная может принимать значение, большее чем исходная величина. Это касается показателей продаж на стадии строительства, при которой рассчитывается доля очередей на стадии строительства, следовательно, и продаж. Далее модель автоматически рассчитывает оставшуюся часть площадей и рассчитывает темп продаж, исходя из переменной TK. В конечном итоге, суммарная продаваемая площадь может быть больше, чем вводная SK. Это недопустимо, поскольку предельная продаваемая площадь объектов определена на стадии подготовки исходно-разрешительной документации и не подлежит оценке в рамках экономико-математической модели [3, 6, 7].

Так как метод обобщенного понижающего градиента предполагает ввод переменных, которые приближены к оптимальным вариантам (на основе экспертной оценки), то необходимо провести оценку оптимальной ставки по проектному финансированию. Для этого необходимо использовать линейную интерполяцию между минимальными и максимальным значениями темпом продаж.

Для подбора значения, наиболее близкого к оптимальному, необходимо вносить данные в ячейки 10 раз. Это позволяет соблюсти шаг в 500 рублей и максимально оптимизировать целевую функцию.

Для расчета денежного потока на основании полученных с помощью целевой модели переменных, используется инструмент Excel, где потоки рассчитаны за каждый месяц. Ввиду невозможности представить в работе рабочий лист Excel, приводятся основные строки модели для расчета NPV.

На рисунке 1 наглядно представлены основные вводные параметры для расчета оптимальных значений первичных переменных, уровня роста цен, инфляции. Также в данном блоке подробно описываются технико-экономические показателя данного проекта.

Рис. 1. Скриншот экономико-математической модели оценки инвестиционного проекта Источник: составлено авторами

Таким образом, предлагаемая экономико-математическая модель с расчетом NPV и вводных перемененных с помощью метода интерполяции позволяет в дальнейшем с помощью встроенного в продукт Excel провести пошаговое решение задачи оптимизации. Результатом является оптимальные значения вводных переменных, при которым значение NPV, абсолютной и удельной чистой прибыли максимально.

С целью определения эффективности применения предложенной экономико-математической модели, необходимо провести оценку проекта «Каширинский рынок».

Текущий план проекта предполагает реализацию жилья комфорт-класса, однако в текущих макроэкономических условиях необходима оценка адекватности выбора такого варианта. Ввиду снижения уровня реальных располагаемых доходов населения и других факторов, спрос на жилье в новостройках демонстрирует стагнацию и восстановление объемов может длиться продолжительное время. В связи с этим, для расчета эффективности реализации данного проекта будет использовано три различных варианта: эконом-класс, комфорт-класс, бизнес-класс.

Среднегодовой прогноз цен на жилье предоставлен фондом «Институт экономики города». На основании данных вносится прогнозное значение роста в 2023-2025 годах на уровне 3% в год, далее 5% в год. Ставка дисконтирования для расчета приведенных чистых денежных потоков компании вводится на уровне 10%. Источником для данного уровня является экспертное мнение нескольких аналитических компаний (таблица 5).

Результаты решения уравнений линейной интерполяции для эконом-класса представлен на рисунке 2.

На рисунке 3 представлены результаты решения уравнений линейной интерполяции для комфорт-класса. Для бизнес-класса на рисунке 4.

На основе решения уравнений линейной интерполяции получены следующие оптимальные значения вложений в маркетинг, темпа продаж и процентной ставки заемного финансирования (таблица 6).

При моделировании инвестиционного проекта методов бюджетирования данные значения будут наиболее оптимальными и приведут к максимизации чистой прибыли. Далее рассчитаны денежные потоки строительной организации, свободный денежный поток (FCFF) за весь период и дисконтированный денежный поток или чистая приведенная стоимость (NPV). Дополнительно необходимо рассчитать чистую прибыль (Net Profit), которая будет равна значению FCFF и значение чистой прибыли в пересчете на один кв. м. продаваемой площади (S-Net Profit). Все расчеты проведены с использованием программного продукта Excel. Результаты приведены в таблице 7.

Таблица 5

Вводные данные о расходах, цене реализации, объеме продаваемой площади, темпе продаж при различных вариантах класса жилья

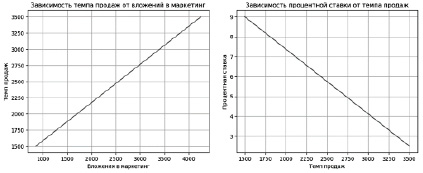
Рис. 2. Графическая интерпретация результата решения уравнения линейной интерполяции в эконом-классе (Python 3, Jupiter Notebook)

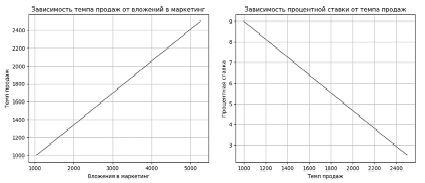
Рис. 3. Графическая интерпретация результата решения уравнения линейной интерполяции в комфорт-классе (Python 3, Jupiter Notebook)

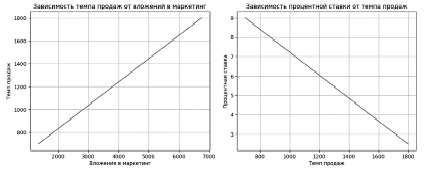
Рис. 4. Графическая интерпретация результата решения уравнения линейной интерполяции в бизнес-классе (Python 3, Jupiter Notebook)

Таблица 6

Оптимальные значения вложений в маркетинг, темпа продаж и процентной ставки заемного финансирования

Таблица 7

Результаты первичного расчета NPV и Net Profit

Таблица 8

Итоговые результаты применения метода обобщенного понижающего градиента для оптимизации целевой функции NPV

На основании полученных данных можно сделать следующие выводы:

а) Эконом-класс при заданных параметрах является наиболее эффективным проектом с точки зрения максимизации прибыли, поэтому данный вариант необходимо рассчитать с помощью метода ОПГ;

б) Комфорт-класс при заданных параметрах является эффективным проектов, поэтому данный вариант необходимо рассчитать с помощью метода ОПГ;

в) бизнес-класс при максимально возможных значениях темпа продаж и вложений в маркетинг демонстрирует минимальные значения NPV и чистой удельной прибыли, поэтому для дальнейшего расчета этот вариант рассматривать не целесообразно.

Последним этапом является расчет для каждого варианта реализации проекта (эконом, комфорт) оптимального значения, при котором денежные потоки будут генерироваться равномерно, чтобы учитывать LLCR – показатель обеспеченности кредита будущими ожидаемыми денежными потоками проекта.

Выбор варианта реализации проекта в эконом-классе после первичного расчета NPV не целесообразен и не сходится с положением строительной организации на рынке, при которой строительная организация реализует проекты комфорт-класса. Это позволяет строительной организации иметь высокую степень удовлетворенности клиентов и иметь конкурентное преимущество на локальном рынке.

Для варианта реализации проекта эконом-класса оптимальными значениями темпа продаж и вложений в маркетинг являются:

а) темп продаж – 2 500 кв. м./мес.;

б) вложения в маркетинг – 3 036 руб./кв. м.

Для варианта реализации проекта комфорт-класса оптимальными значениями темпа продаж и вложений в маркетинг являются:

а) темп продаж – 2 335 кв. м./мес.;

б) вложения в маркетинг – 4 905 руб./кв. м.

Итоговые результаты решения задачи оптимизации методом обобщенного понижающего градиента представлены в таблице 8.

На основании полученных данных можно судить о том, что применение данного метода позволяет определить наиболее оптимальный вариант реализации инвестиционного проекта, с точки зрения класса проекта, переменных расходов и темпа продаж, которое определяет ставку проектного финансирования.

Выводы

Применение экономико-математических методов и имитационного моделирования позволяет объективно оценивать инвестиционные проекты, определять оптимальные размеры инвестиций и доходность, а также минимизировать сроки возврата вложений. Исследование портфеля строительной организации показало, что использование современных методов, в том числе метода обобщенного понижающего градиента для оптимизации NPV, способствует принятию обоснованных управленческих решений, минимизации рисков и успешной реализации проектов. Это особенно важно в строительной отрасли, где введение эскроу-счетов увеличивает потребность в кредитных средствах. Эти подходы повышают эффективность использования ресурсов и помогают привлекать дополнительное финансирование, что значительно улучшает конкурентоспособность и устойчивость строительных организаций на рынке.

Ключевым итогом являются демонстрация эффективности применения экономико-математических методов и современных подходов к оценке инвестиционных проектов. Использование моделирования и оптимизационных методов, таких как метод обобщенного понижающего градиента, позволяет объективно оценивать и выбирать оптимальные варианты реализации проектов. Это способствует принятию обоснованных инвестиционных решений, минимизации рисков и успешной реализации проектов, особенно в условиях неопределенности и высокой конкуренции на рынке. В результате строительные организации могут более эффективно использовать инвестиционные ресурсы и привлекать дополнительные источники финансирования, что особенно актуально для строительной отрасли.