Введение
Современная экономика находится в процессе постоянных изменений, организации осознают, что им приходится реагировать на каждое изменение, заранее предвидя следующее. Их ответные меры часто принимают форму проектов. Поэтому умение эффективно управлять проектами стало необходимостью. Важными вопросами являются не только то, когда следует применять проектный подход и как работать с самим проектом, но даже то, что на самом деле представляет собой проект. Кубасова Т.И. рассматривает проект как управляемое изменение исходного состояния любой системы, связанное с затратами времени и средств, которое достигается использованием средств ресурсного обеспечения и подпадает под действие ограничений [2].
Одним из самых распространенных проблем, с которым сталкивается руководитель и команда проекта является плохая организация планирования проекта [4]. Для оценки эффективности планирования необходимо выработка методики оценки на основе объективных количественных данных [1]. Проблема планирования проекта с ограниченными ресурсами (RCPSP) широко применима во многих областях, таких как управление проектами, строительство и планирование производства [7]. RCPSP минимизирует общую продолжительность проекта в зависимости от соотношения приоритетов между видами деятельности и ресурсных ограничений [10].
Целью исследования является определить схему планирования, которая минимизирует продолжительность проекта с учетом всех трех временных ограничений.
RCPSP с обобщенными отношениями приоритета является расширением RCPSP. Обобщенные отношения приоритета (GPRs) – это временные ограничения, при которых время начала/окончания пары работ должно быть разделено по меньшей мере или не более чем на промежуток времени, обозначаемый как временная задержка (минимальная временная задержка и максимальная временная задержка соответственно). Ли и Донг [9] изучили многомодовое выравнивание ресурсов в проектах с зависящими от режима обобщенными отношениями приоритета (MRLP-GPR) и предложили два подхода к решению: декомпозицию и интеграцию. Де Азеведо и др. [6] предложили точный метод, основанный на выполнимости и рабочей нагрузке, для решения проблемы планирования проекта с ограниченными ресурсами с обобщенными ограничениями приоритета (RCPSP/MAX). Бьянко и Карамия [5] предложили новый алгоритм ветвления и привязки для задачи планирования проекта с ограниченными ресурсами с обобщенными отношениями приоритета (RCPSP/GPRs) и целью минимального времени выполнения.
Во всех этих исследованиях использовались методы преобразования для GPRs: временные задержки от начала до конца, от финиша до старта и от финиша до финиша могут быть преобразованы в задержки от начала до старта. Следовательно, работы зависят от GPRs, которые относятся к минимальным и максимальным задержкам между временем начала действий. Однако в процессе планирования время выполнения работы не обязательно является фиксированным значением.
RCPSP с календарями ресурсов учитывает время отсутствия ресурсов, что является проблемой, очень близкой к реальному промышленному проекту. В настоящее время исследований RCPSP с календарями ресурсов проводится мало. Чжан [11] представил метод планирования времени для составления расписания проекта с использованием одного и того же календаря для каждого типа ресурсов. Кретер и др. [8] определили проблему RCPSP для решения проблем планирования проекта с ограничениями календаря ресурсов с целью минимизации продолжительности проекта. Однако они преобразовали остальные три отношения приоритета в отношения приоритета от старта до старта.
Насколько нам известно, не существует литературы по RCPSP с одновременным ограничением продолжительности работы, временным ограничением на выполнение работы и ограничением ресурсов по календарю. Эту проблему можно назвать RCPSP при множественных временных ограничениях (RCPSP/MTC).
Материал и методы исследования
Ограничение продолжительности работы
В процессе планирования и из-за ограниченности ресурсов, используемых для выполнения работы, продолжительность работы может потребоваться увеличить. Например, работа i выполняется работником A, и для завершения i требуется не менее 7 дней.
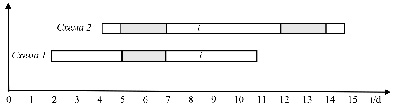
Рис. 1. Два варианта планирования
Работник A работает не каждый день; он будет отдыхать в дни 5-7 и 12-14. Таким образом, в процессе составления графика продолжительность работы i может быть увеличена. Как показано на рис. 1, схема 1 и схема 2 представляют собой два допустимых расписания выполнения работы i в условиях ограниченности ресурсов, в данном случае работника А, и их продолжительность была увеличена до 11 и 9 дней соответственно. Однако, если существует верхний предел времени для работы i, некоторые возможные схемы расписания будут неосуществимы. Например, если из-за ограничений, накладываемых на работу i, продолжительность работы i не должна превышать 10 дней, то схема 2 станет неосуществимым решением.
Верхний предел времени продолжительности работы также важен при планировании и должен приниматься во внимание при разработке расписания проекта. Продолжительность xi работы i может быть выражена следующим выражением:
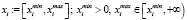 (1)
(1)
Временные ограничения на задержку работ
Обобщенные отношения приоритета (GPRs) – это временные ограничения, при которых время начала/окончания пары работ должно быть разделено по меньшей мере или не более чем на промежуток времени, обозначаемый как временная задержка, соответственно минимальная временная задержка и максимальная временная задержка. GPRs можно разделить на отношения «начало-начало» (SS), «начало-конец» (SF), «конец-начало» (FS) и «конец-конец» (FF). Эти четыре типа ограничений удваиваются, когда речь идет о минимальном и максимальном временном запаздывании. В частности, минимальное временное запаздывание порождает
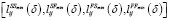 ,
,
которые указывают, что работа j может начаться (завершиться) только в том случае, если его предшественник i был начат (завершен) по крайней мере на δ единиц времени раньше. Аналогично, максимальная задержка по времени
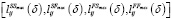
устанавливает, что работа j может быть начато (завершено) не более чем через δ единиц времени после времени начала (окончания) работы i. В настоящее время для удобства расчетов временные задержки от старта до финиша, от финиша до старта и от финиша до финиша необходимо сначала преобразовать в временные задержки от старта до старта. Этот метод преобразования требует важного допущения, что каждая работа i имеет фиксированное время выполнения xi. Однако в процессе планирования время выполнения xi работы i не обязательно является фиксированным значением, и это может быть из-за такого фактора, как календари ресурсов. Можно сказать, что этот метод преобразования может давать искаженные результаты.
Как показано на рис. 2, между работами i и j существует приоритет FS, а минимальная и максимальная задержки равны 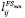 и
и 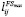 . Si и Fi – это время начала и окончания работы i, а Sj и Fj – время начала и окончания работы j. Время выполнения работы i равно xi, и Fi = Si + xi. Время окончания работы i и время начала работы j находятся в следующей зависимости:
. Si и Fi – это время начала и окончания работы i, а Sj и Fj – время начала и окончания работы j. Время выполнения работы i равно xi, и Fi = Si + xi. Время окончания работы i и время начала работы j находятся в следующей зависимости:
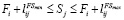 (2)
(2)
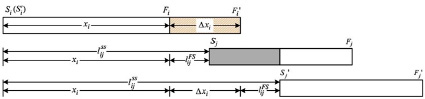
Рис. 2. Анализ неосуществимых ситуаций
Временное окно Sj относительно Fi равно:
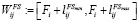 (3)
(3)
Формула соотношения запаздывания от FS к запаздыванию от SS такова:
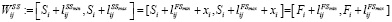 (4)
(4)
Следовательно, временное окно работы j относительно работы i можно выразить через следующее уравнение:
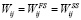 (5)
(5)
Однако при планировании сначала планируется работа i. Из-за влияния такого фактора, как календари ресурсов, время выполнения работы i увеличивается на Δxi. Тем временем время начала и окончания работы i равно Sí и Fí, работа j зависит от работы i, а время начала и окончания работы изменено на Sj́ и Fj́. Временной интервал регулируется следующим образом:
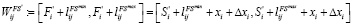 (6)
(6)
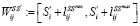 =
= 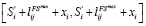 (7)
(7)
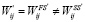 (8)
(8)
Очевидно, что при увеличении времени выполнения работы i, 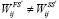 и этот метод преобразования больше не эффективен.
и этот метод преобразования больше не эффективен.
Ограничения в отношении календарей ресурсов
Согласно Руководству по управлению проектами [3] календарь ресурсов указывает рабочие дни, смены, начало и окончание обычного рабочего времени, выходные дни и государственные праздники, когда каждый конкретный ресурс имеется в наличии. Информация о том, какие ресурсы (например, ресурсы команды, оборудование и материалы) потенциально доступны в то время, когда запланированы операции, применяется для оценки использования ресурсов. Календари ресурсов также устанавливают, когда и как долго определенные ресурсы проекта будут доступны на протяжении проекта. Эта информация может находиться на уровне операции или проекта. Сюда относится учет таких параметров, как наличие ресурса и/или уровень навыков, а также особенности различных географических мест нахождения. Следовательно, создание надежного расписания зависит от хорошего понимания доступности каждого ресурса и ограничений по расписанию, включая часовые пояса, часы работы, отпуска, выходные и праздничные дни, графики технического обслуживания и обязательства по другим проектам.
Набор типов возобновляемых ресурсов обозначается символом R, а каждый тип возобновляемого ресурса – k ∈ R. Календарь для ресурса k ∈ R представляет собой пошаговую функцию, следующим образом:
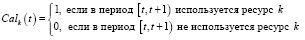 (9)
(9)
Может ли работа i быть выполнено в момент времени t, зависит от того, доступны ли все ресурсы, которые оно использует, в момент времени t. Если Ri указывает набор типов ресурсов, используемых для выполнения работы i, то расписание работ Ci(t) выводится из календарей ресурсов следующим образом:
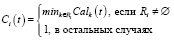 (10)
(10)
При наличии календарей некоторые работы могут быть прерваны на время перерыва в базовом расписании проекта, в то время как другие работы прерывать запрещено. Выполнение работы, которое может быть прервано, должно быть прервано в моменты времени t с Ci(t) = 0, и выполнение должно быть продолжено в следующий момент времени τ > t с Ci(τ) = 1.
Время окончания работы i можно определить по времени начала и календарю мероприятий следующим образом:
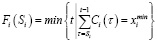 (11)
(11)
Результаты исследования и их обсуждение
В этом разделе мы формально опишем RCPSP/MTC. В дальнейшем мы предполагаем, что проект состоит из набора 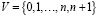 , n ≥ 1 работ, где 0 и n + 1 обозначают начало и конец проекта соответственно. Каждое действие i имеет продолжительность xi ∈ N, верхний предел xi равен
, n ≥ 1 работ, где 0 и n + 1 обозначают начало и конец проекта соответственно. Каждое действие i имеет продолжительность xi ∈ N, верхний предел xi равен 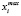 , а нижний предел xi равен
, а нижний предел xi равен 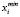 . Работа i, если xi > 0 называется реальной работой, а набор реальных работ обозначается через V r ⊂ V. Работы 0 и n + 1 имеют продолжительность xi = 0 из набора фиктивных работ V f ⊂ V / V r Набор видов возобновляемых ресурсов обозначается символом R, и для каждого типа возобновляемых ресурсов k ∈ R задается ресурсная емкость Rk ∈ N, которая не должна быть превышена ни в один момент времени. Количество ресурсов вида k, которое постоянно используется во время выполнения работы i ∈ V, задается значением rik ∈ N. Для фиктивных работ i ∈ V f значение rik = 0 справедливо для всех k ∈ R. Календарь для ресурса k ∈ R обозначается Calk(t), и календарь работ i ∈ V обозначается Ci(t). Правила расчета Calk(t) и Ci(t) показаны в уравнениях 9 и 10. Si ∈ T указывает время начала, а Fi ∈ T – время окончания операции i ∈ V. Мы предполагаем, что проект начинается в момент времени 0, т.е. S0 = 0. Тогда продолжительность проекта равна Fn+1.
. Работа i, если xi > 0 называется реальной работой, а набор реальных работ обозначается через V r ⊂ V. Работы 0 и n + 1 имеют продолжительность xi = 0 из набора фиктивных работ V f ⊂ V / V r Набор видов возобновляемых ресурсов обозначается символом R, и для каждого типа возобновляемых ресурсов k ∈ R задается ресурсная емкость Rk ∈ N, которая не должна быть превышена ни в один момент времени. Количество ресурсов вида k, которое постоянно используется во время выполнения работы i ∈ V, задается значением rik ∈ N. Для фиктивных работ i ∈ V f значение rik = 0 справедливо для всех k ∈ R. Календарь для ресурса k ∈ R обозначается Calk(t), и календарь работ i ∈ V обозначается Ci(t). Правила расчета Calk(t) и Ci(t) показаны в уравнениях 9 и 10. Si ∈ T указывает время начала, а Fi ∈ T – время окончания операции i ∈ V. Мы предполагаем, что проект начинается в момент времени 0, т.е. S0 = 0. Тогда продолжительность проекта равна Fn+1.
С помощью параметра ρk мы указываем, остаются ли задействованными или блокируются виды возобновляемых ресурсов k ∈ R во время перерывов в работах, которые требуют этих ресурсов (ρk = 1), или освобождаются и могут использоваться для выполнения других работ во время перерывов (ρk = 0).
Параметр S = (S0, S1, … Sn+1), определяющее время начала всех действий, называется расписанием.
Учитывая расписания и момент времени t, набор всех реальных работ i ∈ V r, которые выполняются в момент времени t, называется активным набором и может быть определен с помощью
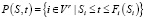 .
.
Тогда, использование 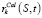 ресурса k ∈ R в момент времени t в соответствии с расписанием S может быть вычислено с помощью:
ресурса k ∈ R в момент времени t в соответствии с расписанием S может быть вычислено с помощью:
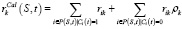 (12)
(12)
С помощью введенных обозначений можно получить следующую математическую формулировку для RCPSP/MTC:
Минимизировать Fn+1 (13)
При условии 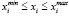 , i ∈ V (14)
, i ∈ V (14)
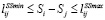 , i, j ∈ V (15)
, i, j ∈ V (15)
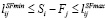 , i, j ∈ V (16)
, i, j ∈ V (16)
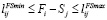 , i, j ∈ V (17)
, i, j ∈ V (17)
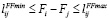 , i, j ∈ V (18)
, i, j ∈ V (18)
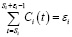 , i ∈ V (19)
, i ∈ V (19)
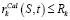 , k ∈ R (20)
, k ∈ R (20)
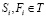 , i ∈ V (21)
, i ∈ V (21)
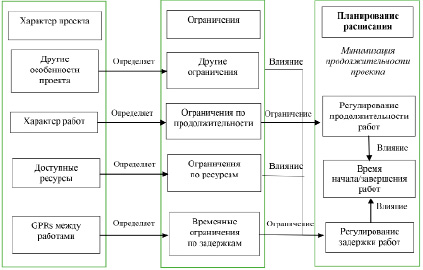
Рис. 3. Схема планирования при множественных временных ограничениях
Цель RCPSP/MTC – найти график, который минимизирует продолжительность проекта [уравнение (12)] и удовлетворяет ограничениям по продолжительности работ [уравнение (13)], временным ограничениям [уравнения (14)–(17)], ограничения по ресурсным календарям [уравнение (18)] и ресурсным возможностям [уравнение (19)].На рис. 3 показана структура для решения RCPSP/MTC и проиллюстрирована взаимосвязь между несколькими ограничениями.
Заключение
В этой статье мы представляем новую практическую задачу планирования, называемую задачей планирования проекта с ограниченными ресурсами в условиях множественных временных ограничений (RCPSP/MTC).
Цель RCPSP/MTC состоит в том, чтобы минимизировать общий срок реализации проекта с учетом ограничений на продолжительность деятельности, временных ограничений и календарных ограничений ресурсов.
RCPSP/MTC вносит свой весомый вклад в разработку практической системы поддержки принятия решений для устранения реальных ограничений в различных проектах.

