Целью исследования является разработка достоверных эконометрических моделей для оценки результатов успеваемости студентов как критерия качества получаемого образования, а также выявление факторов, влияющих на успеваемость, посещаемость студентов и отчисление из вуза. Исследование факторов, влияющих на конкурентоспособность будущего выпускника уже поднималась в научной литературе и в настоящее время в свете современных социально-экономических преобразований звучит как никогда актуально [1, 2]. Качество образования и конкурентоспособность выпускников тесно взаимосвязана с риск-ориентированным регулированием российских вузов и должны использоваться в государственном регулировании образовательной деятельности [3].
Эмпирическая задача состояла в построении статистических нейросетевых моделей различных видом. Для проведения анализа были использованы инструменты многомерной статистики и нейронных сетей в пакете Statistica, программирование в среде R, которые уже доказали свою достоверность и надежность [4].
Материалы и методы исследования
Основным информационным источником для проведения исследования стали данные проведенного анкетирования среди студентов экономического, физико-математического и электроэнергетического факультетов, также данные по отчисленным студентам, представленным деканатами ЭФ и ФМФ Института цифровых технологий Марийского государственного университета.
Сбор данных производился посредством онлайн анкетирования студентов в течение двух месяцев (март и апрель) 2023 года.
В анкетировании принимали участие студенты 38 учебных групп. Каждой группе был присвоен индивидуальный код. В исследовании приняли участие студенты по следующим направлениям и профилям:
• 01.03.01 Математика (Математические и инструментальные методы в экономике),
• 01.03.01 Математика (Математические методы в экономике),
• 01.03.01 Математика (Математическое моделирование, нейросетевые технологии и анализ больших данных),
• 02.03.03 Математическое обеспечение и администрирование информационных систем (Интеллектуальные системы и базы данных),
• 03.03.02 Физика (Медицинская физика),
• 09.02.07 Информационные системы и программирование (СПО),
• 09.03.02 Информационные системы и технологии (Разработка мобильных и web-приложений),
• 09.03.02 Информационные системы и технологии (Современные радиолокационные системы дальнего обнаружения),
• 13.03.02 Электроэнергетика и электротехника (Электроснабжение по отраслям),
• 22.02.01 Материаловедение и технологии материалов (Технология производства радиоэлектронной компонентной базы и систем),
• 38.03.01 Экономика (Бизнес-статистика и аналитика),
• 38.03.01 Экономика (Финансовая и прикладная экономика),
• 38.03.01 Экономика (Цифровая экономика),
• 43.03.01 Сервис (Сервисная деятельность в бизнесе),
• 43.03.01 Сервис (Управление бизнесом),
• 43.03.01 Сервис (Цифровой маркетинг и бизнес-аналитика).
Всего в анкетировании принимали участие 290 студентов. По каждому студенту были собраны данные по 12 параметрам, качественные показатели были переведены в количественные. Список параметров и их расшифровка представлены в таблице (таблица 1).
Таблица 1
Переменные для моделей
|
Независимая переменная |
Расшифровка значений (кодирование переменных) |
|
Форма финансирования |
1 – Бюджет; 0 – Внебюджет |
|
Курс |
Первый – 1; Второй – 2; Третий – 3; Четвертый – 4 |
|
Пол |
Мужской – 1; Женский – 0 |
|
Возраст |
17 – 1; 18 – 2; 19 – 3; 20 – 4; 21 – 5; 22 – 6; 23 – 7; 33 – 8 |
|
Территориальное происхождение |
Город – 1; Сельская местность – 2; Другая страна – 3 |
|
Общежитие |
Проживаю – 1; Не проживаю – 0 |
|
Количество пропусков |
|
|
Количество долгов |
|
|
Средний балл зачётной книжки |
|
|
Результаты ЕГЭ |
|
|
Средний балл по аттестату |
В рамках исследования были рассмотрены две модели. В первой, в качестве зависимой переменной выступает показатель «количество академических долгов», а во второй – показатель «количество пропусков». Для каждой из моделей были построены нейросетевые модели.
Результаты исследования и их обсуждение
Рассмотрим результаты построения нейросетевых моделей, описывающих зависимость «Количества долгов» от вышеперечисленных независимых переменных. Для определения наиболее точной регрессионной модели были рассмотрены несколько типов нейронных сетей:
• Linear – линейная нейронная сеть.
• MLP – многослойный персептрон.
• RBF – нейронная сеть радиально-базисных функций.
• GRNN – обобщенная нейронная сеть.
Всего было проанализировано 20 сетей (каждой нейронной сети был присвоен условный порядковый номер от 1 до 20) различных типов и с различным количеством слоев и нейронов на слое. Результатом анализа явились 5 нейронных сетей, имеющих наивысшую точность. Результат представлен в таблице (таблица 2).
Наилучшей регрессионной нейросетевой моделью зависимости количества академических долгов от заданных переменных является модель многослойного персептрона с одним входным, двумя скрытым и одним выходным слоем, с пятью нейронами на входном слое, десятью и четырьмя на скрытых слоях и одним нейроном на выходном слое (нейронная сеть с порядковым номером восемь). Точность модели на тестовой выборке равна 88%. В пятерку лучших нейросетей также входят как линейные нейронные сети, так и многослойные персептроны.
Ниже представлены описательные параметры построенных регрессионных нейросетевых моделей (таблица 3) и их графическая реализация (рисунок 1). Из описательных параметров моделей можно сделать вывод о том, что средняя ошибка моделирования не превышает 3%. У наилучшей модели с порядковым номером восемь средняя ошибка моделирования равна 0,6%.
Теперь перейдем к анализу чувствительности построенных моделей (таблица 4). Наибольшее влияние на зависимую переменную лучшей модели оказывают такие факторы, как «Пол» и «Средний балл по аттестату».
Графическое представление построенных нейронных сетей отображено на рисунке 1.
Таблица 2
Наилучшие регрессионные модели
|
№ |
Архитектура сети |
Производ. обучения |
Контрольн. производит. |
Тест. производ. |
Ошибка обуч. |
Контрольн. ошибка |
Тест. ошибка |
Входы |
Скрытый слой №1 |
Скрытый слой №2 |
|
6 |
Linear 2:2-1:1 |
0,943 |
0,945 |
1,047 |
0,176 |
0,119 |
0,126 |
2 |
0 |
0 |
|
7 |
Linear 3:3-1:1 |
0,911 |
0,921 |
1,022 |
0,170 |
0,116 |
0,125 |
3 |
0 |
0 |
|
8 |
MLP 5:5-10-4-1:1 |
0,733 |
0,914 |
1,048 |
0,137 |
0,115 |
0,124 |
5 |
10 |
4 |
|
9 |
MLP 3:3-4-1:1 |
0,788 |
0,888 |
1,064 |
0,147 |
0,112 |
0,127 |
3 |
4 |
0 |
|
10 |
MLP 5:5-10-7-1:1 |
0,729 |
0,875 |
1,072 |
0,136 |
0,110 |
0,128 |
5 |
10 |
7 |
Таблица 3
Параметры регрессии (здесь номера – это номера моделей)
|
Параментры модели |
Количество долгов.6 |
Количество долгов.7 |
Количество долгов.8 |
Количество долгов.9 |
Количество долгов.10 |
|
Среднее |
0,142 |
0,142 |
0,142 |
0,142 |
0,142 |
|
Стандартное отклонение |
0,476 |
0,476 |
0,476 |
0,476 |
0,476 |
|
Средняя ошибка |
0,023 |
0,027 |
-0,006 |
0,012 |
0,013 |
|
Ст.откл.ошибки |
0,456 |
0,442 |
0,386 |
0,403 |
0,384 |
|
Абс.средн.ошибки |
0,268 |
0,278 |
0,215 |
0,202 |
0,200 |
|
Отношение ст.откл. |
0,956 |
0,929 |
0,811 |
0,845 |
0,806 |
|
Корреляция |
0,299 |
0,378 |
0,586 |
0,536 |
0,593 |
Таблица 4
Анализ чувствительности регрессионных моделей (здесь номера – это номера моделей)
|
Параметры модели |
Пол |
Территориальное происхождение |
Количество пропусков |
Средний балл зачётной книжки |
Средний балл по аттестату |
|
Отношение.6 |
1,015 |
1,028 |
|||
|
Ранг.6 |
2,000 |
1,000 |
|||
|
Отношение.7 |
1,005 |
1,028 |
1,033 |
||
|
Ранг.7 |
3,000 |
2,000 |
1,000 |
||
|
Отношение.8 |
1,124 |
1,107 |
1,013 |
1,066 |
1,117 |
|
Ранг.8 |
1,000 |
3,000 |
5,000 |
4,000 |
2,000 |
|
Отношение.9 |
1,075 |
1,026 |
1,092 |
||
|
Ранг.9 |
2,000 |
3,000 |
1,000 |
||
|
Отношение.10 |
1,041 |
1,102 |
1,050 |
1,054 |
1,136 |
|
Ранг.10 |
5,000 |
2,000 |
4,000 |
3,000 |
1,000 |
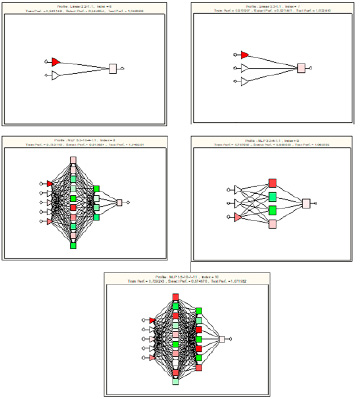
Рис. 1. Графическое представление построенных нейронных сетей по показателю «количество академических долгов» Источник: построено авторами с использованием программы Statistica 7.0
Проверка результатов применения выбранных моделей была проведена на нескольких условных примерах.
1. Студент имеет следующие параметры: пол: мужской, территориальное происхождение: другая страна, количество пропусков: 0, средний балл зачетной книжки: 3, средний балл по аттестату 3, количество долгов у данного студента равно 3. Значение зависимой переменной равно 2.89.
2. Студент имеет следующие параметры: пол: мужской, территориальное происхождение: сельская местность, количество пропусков: 3, средний балл зачетной книжки: 3, средний балл по аттестату 4, количество долгов у данного студента равно 1. Значение зависимой переменной равно 0.7.
3. Студент имеет следующие параметры: пол: женский, территориальное происхождение: город, количество пропусков: 2, средний балл зачетной книжки: 4, средний балл по аттестату 5, количество долгов у данного студента равно 0. Значение зависимой переменной равно 0.01.
Перейдем к анализу второго показателя «количество пропусков» и рассмотрим построение нейросетевых моделей, описывающих зависимость «количества пропусков» от вышеперечисленных независимых параметров. Как и в случае с «количеством долгов», для определения наиболее точной регрессионной модели были рассмотрены несколько типов нейронных сетей: Linear, MLP, RBF и GRNN. Было проанализировано 20 сетей различных типов и с различным количеством слоев и нейронов на слое. Результатом анализа явились 5 нейронных сетей, имеющих наивысшую точность. Результат представлен в таблице 5.
Рассмотрим параметры построенных моделей, представленные в таблице 5. Анализируя таблицу, авторы пришли к выводу о том, что наилучшей регрессионной моделью для оценки количества пропусков является модель №4 – это модель радиально-базисных функций с четырьмя нейронами на входном слое, 11 нейронами на скрытом слое и одним выходным нейроном (таблица 6).
На тестовой выборке, точность модели составила 95%, а средняя ошибка модели составила 18%.
Таблица 5
Наилучшие регрессионные модели
|
№ |
Архитектура сети |
Производ. обучения |
Контрольн. производит. |
Тест. производ. |
Ошибка обуч. |
Контрольн. ошибка |
Тест. ошибка |
Входы |
Скрытый слой №1 |
Скрытый слой №2 |
|
1 |
GRNN 4:4-121-2-1:1 |
0,803 |
0,925 |
0,831 |
0,049 |
0,072 |
0,050 |
4 |
121 |
2 |
|
2 |
RBF 4:4-4-1:1 |
0,864 |
0,915 |
0,866 |
0,053 |
0,071 |
0,052 |
4 |
4 |
0 |
|
3 |
GRNN 4:4-121-2-1:1 |
0,871 |
0,910 |
0,890 |
0,054 |
0,070 |
0,053 |
4 |
121 |
2 |
|
4 |
RBF 4:4-11-1:1 |
0,819 |
0,905 |
0,859 |
0,050 |
0,070 |
0,052 |
4 |
11 |
0 |
|
5 |
RBF 4:4-8-1:1 |
0,789 |
0,900 |
0,780 |
0,049 |
0,070 |
0,047 |
4 |
8 |
0 |
Таблица 6
Параметры регрессии (здесь номера – это номера моделей)
|
Количество пропусков.1 |
Количество пропусков.2 |
Количество пропусков.3 |
Количество пропусков.4 |
Количество пропусков.5 |
|
|
Среднее |
8,347 |
8,347 |
8,347 |
8,347 |
8,347 |
|
Стандартное отклонение |
17,169 |
17,169 |
17,169 |
17,169 |
17,169 |
|
Средняя ошибка |
-0,580 |
0,556 |
-0,737 |
0,184 |
0,253 |
|
Ст.откл.ошибки |
14,642 |
15,157 |
15,262 |
14,752 |
14,206 |
|
Абс.средн.ошибки |
8,501 |
9,204 |
8,841 |
9,048 |
8,921 |
|
Отношение ст.откл. |
0,853 |
0,883 |
0,889 |
0,859 |
0,827 |
|
Корреляция |
0,558 |
0,470 |
0,541 |
0,512 |
0,562 |
Таблица 7
Анализ чувствительности регрессионных моделей (здесь номера – это номера моделей)
|
Параметры модели |
Возраст |
Количество долгов |
Результаты ЕГЭ |
Средний балл по аттестату |
|
Отношение.1 |
1,021 |
1,018 |
1,038 |
1,107 |
|
Ранг.1 |
3,000 |
4,000 |
2,000 |
1,000 |
|
Отношение.2 |
1,016 |
0,996 |
1,003 |
1,048 |
|
Ранг.2 |
2,000 |
4,000 |
3,000 |
1,000 |
|
Отношение.3 |
1,019 |
1,027 |
1,023 |
1,072 |
|
Ранг.3 |
4,000 |
2,000 |
3,000 |
1,000 |
|
Отношение.4 |
1,019 |
1,002 |
1,010 |
1,086 |
|
Ранг.4 |
2,000 |
4,000 |
3,000 |
1,000 |
|
Отношение.5 |
1,015 |
0,991 |
1,000 |
1,172 |
|
Ранг.5 |
2,000 |
4,000 |
3,000 |
1,000 |
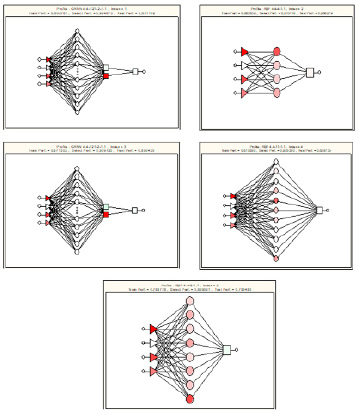
Рис. 2. Графическая реализация построенных моделей по показателю «количество пропусков» Источник: построено авторами с использованием программы Statistica 7.0
Анализ чувствительности модели показал, что на количество пропусков занятий студентом, наибольшее влияние оказывает «Средний балл по аттестату» и «Возраст», а наименьший «Количество долгов» (таблица 7).
На рисунке 2 представлены графические реализации построенных моделей.
Проверка результатов применения выбранных моделей была проведена на нескольких условных примерах.
1. Студент имеет следующие параметры: возраст: 19 лет, количество долгов: 0, результаты ЕГЭ: 251 балл, средний балл по аттестату: 5, количество пропусков у данного студента равно 3. Значение зависимой переменной равно 3.29.
2. Студент имеет следующие параметры: возраст: 18 лет, количество долгов: 0, результаты ЕГЭ: 218 баллов, средний балл по аттестату: 4.8, количество пропусков у данного студента равно 8. Значение зависимой переменной равно 7.35.
3. Студент имеет следующие параметры: возраст: 19 лет, количество долгов: 0, результаты ЕГЭ: 211 балл, средний балл по аттестату: 4.8, количество пропусков у данного студента равно 6. Значение зависимой переменной равно 5.20.
Заключение
Резюмирую вышеизложенное можно сделать следующие выводы.
Наилучшей регрессионной нейросетевой моделью зависимости количества академических долгов от заданных переменных является модель многослойного персептрона с одним входным, двумя скрытым и одним выходным слоем, с пятью нейронами на входном слое, десятью и четырьмя на скрытых слоях и одним нейроном на выходном слое (нейронная сеть с порядковым номером восемь). Точность модели на тестовой выборке равна 88%. В пятерку лучших нейросетей также входят как линейные нейронные сети, так и многослойные персептроны.
Наибольшее влияние на зависимую переменную лучшей модели оказывают такие факторы, как «Пол» и «Средний балл по аттестату».
Наилучшей из всех нейросетевых моделей, описывающих зависимость «Количества пропусков» от вышеперечисленных независимых параметров является модель радиально-базисных функций с четырьмя нейронами на входном слое, 11 нейронами на скрытом слое и одним выходным нейроном.
Анализ чувствительности модели показал. Что на количество пропусков занятий студентом, наибольшее влияние оказывает «Средний балл по аттестату» и «Возраст», а наименьший «Количество долгов».
Проверка построенных моделей на примерах доказала их практическую значимость.

