Введение
Исследования экономических процессов методами, применяемыми при решении физических задач, начались с середины 1990-ых годов. В научной литературе появилось много работ (см., например, [1-3] и приведенный там список литературы), в которых авторы стараются экономические задачи различного характера решить, используя теорию и методы, разработанные физиками для решения задач в области физики. Работа [4] посвящена применению методов статистической физики к экономическим системам (в частности, для описания финансовых систем). Авторы работы [5] считают возможным экономический закон спроса и предложения объяснить с помощью физического закона сохранения матери и энергии. В работе [6] автором предложены теоретико-методологические основы физической экономики. Приведены определения скорости, силы, энергии, ускорения в экономике. Работы [7-8] посвящены исследованию динамики изменения национального дохода в модели гармонического осциллятора с возмущением без учета трансакционных издержек (затухание отсутствует) и с учетом последних (затухание присутствует). В настоящей работе решается аналогичная задача в предположении, что внешние инвестиции линейно зависят от времени.
Целью исследования является анализ динамики изменения национального дохода в зависимости от времени в предположении, что национальный доход удовлетворяет обыкновенному дифференциальному уравнению гармонического осциллятора с правой частью.
Постановка задачи и ее решение
Пусть национальный доход как функция от времени (Y(t)) удовлетворяет дифференциальному уравнению гармонического осциллятора с внешним воздействием (внешние инвестиции) без учета трансакционных издержек (коэффициент затухания η = 0). Предполагая, что внешние инвестиции в зависимости от времени меняются по линейному закону, получим, что Y(t) удовлетворяет следующему обыкновенному неоднородному дифференциальному уравнению с постоянными коэффициентами второго порядка
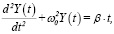(1)
где первый член уравнения d2Y(t)/dt2 – темп изменения национального дохода, второй член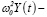 
рыночная сила, ω0 – собственная частота осциллятора, βt – внешние инвестиции, β > 0 – темп роста инвестиций.
Если при решении уравнения (1) пользоваться методом Эйлера и методом вариации произвольных постоянных [9], то для определения неизвестных функций c1(t) и c2(t), входящих в следующее выражение частного решения неоднородного уравнения (1)
Yч.н.(t)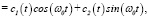 
(2)
получим систему уравнений
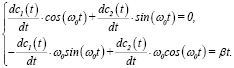(3)
Решение (3) имеет вид:
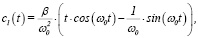(4)
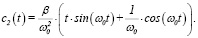(5)
Как известно [12]
Yo.н.(t) = Y(t) = Yo.о.(t) + Yч.н.(t), (6)
где Y(t) = Yo.н.(t) – общее решение неоднородного уравнения (1), Yo.о.(t) – общее решение соответствующего однородного уравнения, Yч.н.(t) – одно частное решение неоднородного уравнения (1). Из (6) с учетом (2), (4), (5) и того факта, что
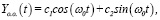
где c1 и c2 – произвольные постоянные, получим
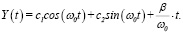(7)
Коэффициенты c1 и c2 в (7) находятся из начальных условий Коши
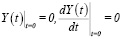(8)
и имеют вид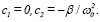 
(9)
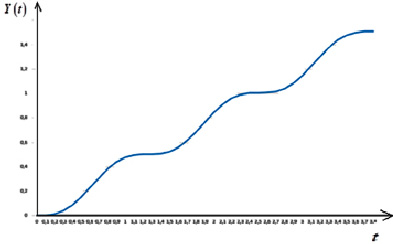
Рис. 1. Зависимость национального дохода от времени согласно (10) при η = 0; ω0 = 5; β = 2; 0 ≤ t ≤ 3,8
Подставляя (9) в (7), для Y(t) получим выражение
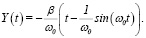(10)
Теперь перейдем к рассмотрению случая, когда не пренебрегаем трансакционными издержками (η ≠ 0). Тогда функция Y(t) будет удовлетворять следующему неоднородному дифференциальному уравнению
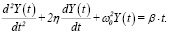(11)
Решение соответствующего однородного уравнения, найденного методом Эйлера (Y(t) = еλt, λ –характеристические числа), приводит к следующим результатам:
а). При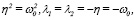 
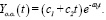(12)
б). При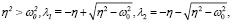 
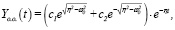(13)
в). При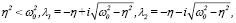 
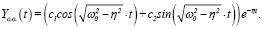(14)
Отметим, что в (12), (13) и (14) c1 и c2 – произвольные положительные постоянные.
Для нахождения одного частного решения уравнения (11) (Yч.н.(t)) в случаях а)., б)., в). будем пользоваться методом подбора. Заметим, что этот метод применим, если правая часть неоднородного дифференциального уравнения имеет вид
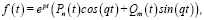(15)
где n = m или n ≠ m.
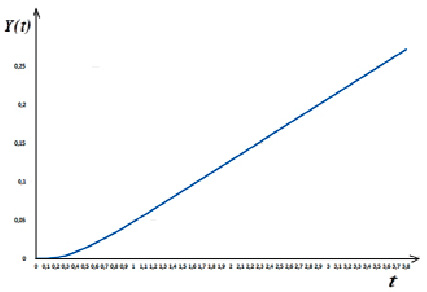
Рис. 2. Зависимость национального дохода от времени согласно (19) при η = ω0 = 5; β = 2; 0 ≤ t ≤ 3,8
а). Так как p + iq = 0 ≠ –η = –ω0, то Yч.н.(t) ищем в виде
Yч.н.(t) = A ∙ t + B, (16)
где неизвестные коэффициенты A и B найдем, требуя, чтобы (16) удовлетворяло уравнению (11). Вычисления приводят к следующему:
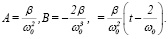(17)
Тогда общее решение уравнения (11) Y(t), согласно (6), имеет вид
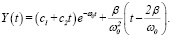(18)
Определяя c1 и c2 из начальных условий Коши (8) и подставляя в (18), получим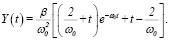 
(19)
б). Так как
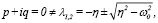
то одно частное решение неоднородного уравнения (11) ищем в виде
Yч.н.(t) = C ∙ t + D, (20)
где C и D пока неизвестные коэффициенты. Выражения для C и D найдем, требуя, чтобы (20) удовлетворяло уравнению (11). Вычисления приводят к следующим значениям
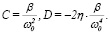(21)
Тогда общее решение неоднородного уравнения (11) примет вид
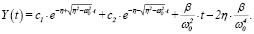(22)
После определения c1 и c2 из начальных условий Коши (см., (8)) (22) приобретает вид
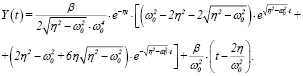(23)
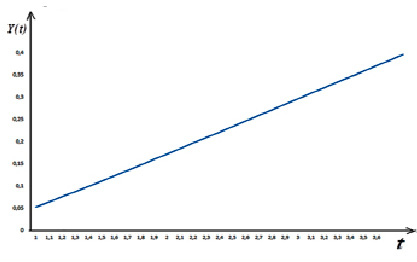
Рис. 3. Зависимость национального дохода от времени согласно (23) при η = 5; ω0 = 4; β = 2; 1 ≤ t ≤ 3,8
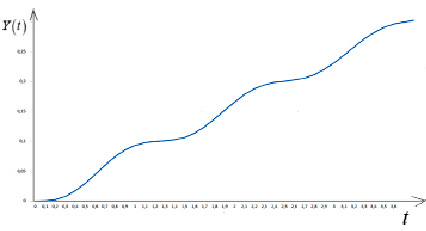
Рис. 4. Зависимость национального дохода от времени согласно (27) при η = 0,1; ω0 = 5; β = 2; 0 ≤ t ≤ 3,8
в). Так как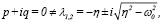 
то аналогично случаю б). получим
Yч.н.(t)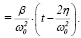 
(25)
Тогда Y(t) будет иметь вид
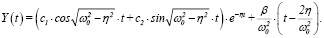(26)
Находя c1 и c2 из начальных условий Коши (см., (8)), для Y(t) в этом случае окончательно имеем
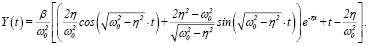(27)
Отметим, что на рисунках 1–4 приведены графики зависимости национального дохода от времени при различных значениях параметров, характеризующих динамику изменения национального дохода в модели гармонического осциллятора, когда внешние инвестиции линейно зависят от времени. Они построены согласно формулам (10), (19), (23) и (27). Рисунки 1 и 4 показывают, что при η = 0 (не учитываем трансакционные издержки) и η < 1 (трансакционные издержки малы), национальный доход в зависимости от времени возрастает, сохраняя колебательный характер. А в случае, когда коэффициент затухания η и частота собственных колебаний осциллятора ω0 величины одного порядка (см., рисунки 2 и 3), то национальный доход в зависимости от времени возрастает по закону линейной функции.
Заключение
В работе исследована зависимость национального дохода от времени в физической модели гармонического осциллятора с внешним воздействием (внешние инвестиции) без учета и с учетом трансакционных издержек. При этом считается, что внешние инвестиции зависят от времени по линейному закону. Графический анализ, проведенный на основе полученных аналитических результатов, показывает, что национальный доход является возрастающей функцией в зависимости от времени. При этом характер возрастания зависит от значений параметров, входящих в выражение, определяющего национальный доход.