Введение
Для решения современных задач управления часто приходится руководствоваться не полной информацией, информацией, носящей вероятностный характер. С одной стороны, если есть возможность провести статистический анализ, то зная закон распределения вероятностей можно по крайней мере определить моментные характеристики среднее, дисперсию и др. В случае же когда определение вероятностных характеристик невозможно, то приходится использовать малоформализованные методы теории игр, исследования операций. Управленческое решение или просто выбор альтернативы осуществляет лицо принимающее решение (ЛПР).
Целесообразно выделить группы задач, в которых основным является оценка вероятности того или иного события. Зная, что сумма вероятностей по всей совокупности событий и их реализаций равна единице, можно предположить распределение вероятностей событий. Самая простая интерпретация таких вероятностей – это весовые коэффициенты событий. Сумма весов также равна единицы. Вероятности могут быть определены хотя бы из тех соображений, что одно событие условно позитивное, может быть предпочтительнее для ЛПР и, следовательно, вероятность может быть выше. Это нестрогое правило выбора может сработать, когда у ЛПР высокое бюджетное ограничение и первый приоритет в выборе альтернатив. Во всех остальных случаях придется рассчитывать, оценивать вероятность того или иного события, выбирать самое эффективное, приемлемое, прибыльное и т.п.
В приложениях в задачах экономики и управления все чаще приходиться иметь дело с ситуацией, когда управленческие решения принимаются в условиях риска и неопределенности. Классические задачи, которые приходится решать участникам рынка это задача конкурентной борьбы и задача разрешения конфликтной ситуации. Эти задачи могут быть успешно решены с помощью теории игр и исследования операций, а также методами линейного программирования если появляется возможность представления задачи теории игр в виде системы ограничений и целевой функции.
В настоящее время значение теории игр существенно возросло во многих областях экономически и управления, при принятии управленческих решений. В экономике теория игр применяется для анализа стратегических проблем предприятий, разработок организационных структур и т.п. Ее можно рассматривать как инструмент, помогающий повысить эффективность плановых и управленческих решений.
С помощью методов и инструментов теории игр можно определить научно обоснованные уровни снижения розничных цен и оптимальный уровень товарных запасов и др. Методы и инструменты теории игр можно применять для анализа конкурентной среды, разрешение конфликтных ситуаций. Сама задача анализа конкурентов может быть интерпретирована как конфликтная задача теории игр [1,2].
Результаты исследования и их обсуждение
Интерпретируя задачу с точки зрения экономики относится к анализу конкурентных стратегий. Несмотря на то, что конкуренты находятся в состоянии риска и неопределенность их решения направленные на максимизацию собственной выгоды, выигрыша подчиняются законам рынка. Следовательно, появляется возможность описать изменение выигрыша с учетом условий конкурентной игры некоторой предельной функций, например функцией полезности.
Предлагается не моделировать функцию, которая может выступать в качестве аппроксимации изменения выигрыша, а предложить готовый аналитический вид такой функции. Выберем для этого функцию полезности Неймана-Моргенштерна как наиболее подходящую для анализа конкурентной борьбы, конфликтной ситуации на рынке. В результате получим формулы, по которым возможно рассчитать вероятности ожидаемого выигрыша через параметры выбранной функции полезности и коэффициенты матрицы игры. Об этом речь пойдет в статье далее.
Для удобства и краткости представления в качестве примера разобрана игра 2×2, однако предложение об использовании функции полезности может быть развито для произвольной размерности m×n матрицы игры. Учтем, что во многих случаях размерность может быть уменьшена за счет исключения из матрицы заведомо не эффективных стратегий, т.е. строк и столбцов матрицы. После того как неэффективные стратегии исключены появляется возможность аналитически выразить выигрыш v через аналитическую функцию полезности.
Материалы и методы исследования
Итак, формализуем конфликтную ситуацию. Пусть у предприятия имеется три способа действий. У предприятия конкурента также три способа действий. В общем случае все это может быть развито для n-мерного варианта (таблица).
Событий при взаимодействии предприятия с конкурентом
|
События предприятия (Ai) |
События конкурента (Bj) |
|||
|
1 |
2 |
3 |
||
|
1 |
0,125 |
0,05 |
0,1 |
|
|
2 |
0,15 |
0,175 |
0,075 |
|
|
3 |
0,1 |
0,125 |
0,025 |
|
Тогда при «вычеркивании» наименее оптимальных вариантов, эта задача сводится к классической задаче 2×2, формула 1. В которой v – это выигрыш, P1,P2 – вероятности соответствующих событий.
 (1)
(1)
В общем виде управленческая, конфликтная задача приводится к оптимизационной задаче в виде системы ограничений и целевой функции. Такое представление задачи конфликта может быть представлена формулой 2
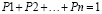
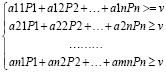 (2)
(2)
Формулу 2 преобразуем и приведем к задаче линейного программирования, формула 3, для этого учтем простой факт, по определению выигрыш v→max, тогда обратная величина выигрыша 1/v→min.
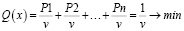
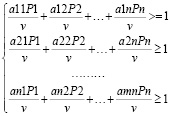 (3)
(3)
При оптимизации матрицы игры после выбраковки стратегий и приведении матрицы к классической форме и размерности 2×2 появляется возможность аналитически решить такую задачу вычислив вероятности событий. Также понимая, что выигрыш v может быть интерпретирован как ожидаемая полезность, то возможно задать v через функцию полезности, например, функцию полезности Неймана-Моргенштерна вида U(x) = ax – bx2. Также удобно то, что известна координата максимума по x это точка с координатой a / 2b.
Если подставить такую функцию полезности в приведенную к размерности 2×2 задачу, предполагая тот факт, что ожидаемый выигрыш v будет аппроксимирован функцией U(x). Для приведенного к наименьшей возможной размерности получим формулу 4.
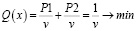
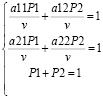 (4)
(4)
Далее подставляем вместо v функцию полезности Неймана-Моргенштерна, предполагая, что участники конфликта как минимум не хотят минимизировать свою ожидаемую полезность. После этой подстановки решаем стандартным способом задачу размерности 2×2 получаем оценки вероятностей через коэффициенты a и b функции Неймана-Моргенштерна в следующем виде, формула 5.
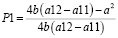 ;
;
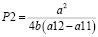 (5)
(5)
Таков подход не нов. Замечено что массовые события, распределённые во времени, могут быть описаны законами распределения случайных величин. Закон распределения может быть аппроксимирован функцией распределения. Подобрав, определив наиболее подходящую функцию появляется возможность вычисления максимального уровня выигрыша v. В этом случае необходимо провести доказательство того, что случайная величина подходит для описания распределения вероятностей. Доказательство обычно проводят с помощью метода наименьших квадратов (МНК) или методом максимального правдоподобия (ММП).
Это аналитическая функция показывает связь между экономическими субъектами, например, конкурентами с тем предположением, что их поведение направлено на максимизацию ожидаемой полезности т.е. как итог выигрыша. Преобразование выигрыша v в виде конкретной функции, желательно непрерывной хотя-бы на отрезке [a, b], позволит вычислить вероятности ожидания выигрыша игроками, конкурентами через параметры этой функции. Также зная вид функции, можно определять без сложных вычислений значение ее экстремумов, что удобно для решения некоторых экономических задач.
В приведенных примерах конфликтные ситуации возникают в результате сознательной деятельности людей. Однако на практике встречаются неопределенности, которые порождаются не сознательным противодействием другой стороны, а недостаточной информированностью об условиях проведения планируемой операции.
Заключение
Чтобы проанализировать конфликтную ситуацию по ее математической модели, ситуацию необходимо упростить, учитывая только важные факторы, влияющие на конфликт и определяющие поведение участников конфликта.
Помимо решения игр в смешанных стратегиях путем применения различных критериев, эффективным способом решения является приведение игровой матрицы к задаче линейного программирования. Что позволяет решить задачу аналитическим способом, например, симплекс-методом. Такой подход возможен и обоснован только с применением ЭВМ.
При этом решение игры сводится к поиску частот выбора той или иной стратегии. Учитывая особенности построения игровой матрицы в задаче конфликтов появляется возможность, во-первых, сократить размерность матрицы, во-вторых, предложить функцию желательно непрерывную которая дает возможность представить в виде функции полезности.
Управленческие решения в экономической деятельности, принимаемые на основе использования теории игр (в особенности игр с природой, поскольку рынок зачастую также не предсказуем), являются наиболее эффективными. Теория игр позволяет выбрать комплекс оптимальных стратегий поведения участников рыночных отношений, выработать оптимальную стратегию поведения на рынке, оптимально про взаимодействовать с конкурентами.
Такие тематические области, как стратегическое поведение, конкуренция, кооперация, риск и неопределенность, являются ключевыми в теории игр и непосредственно связаны с управленческими задачами. Умение грамотно применять законы и методики теории игр упростит решение многих задач и позволит избежать экономических потерь.
Важно отметить, что аппарат теории игр, в отличие от других способов научного предвидения, требующих для расчетов точных характеристик, можно применять и в условиях отсутствия какой-либо информации о возможных действиях соперника, как в случае игр с природой. Это важно, поскольку рынок во многом непредсказуем.
Результаты проведенных при решении задач расчетов позволяют сделать следующие выводы:
- аппарат экономико-математического моделирования (ЭММ) является эффективным инструментом, позволяющим быстрее и качественнее организовать управленческую работу на предприятии;
- теория игр, являясь частью эконометрического анализа, даёт возможность просчитывать ходы предприятия и путем следования правильной стратегии, избежать ошибок и излишних материальных затрат.
В экономической практике нередко приходится формализовать (моделировать) ситуации, придавая им игровую схему, в которых один из участников безразличен к результату игры [7]. В этом случае приходится иметь дело с так называемой статистической игрой. При постановке статистической игры можно допустить, что существует функция распределения выигрыша, следовательно, появляется возможность вычисления моментов этой функции, что существенно облегчает ее анализ и оценку характеристик.
С математической точки зрения выбранная в качестве предельной функция полезности Неймана-Моргенштерна также является частным случаем функции распределения. Исходя из приложений этой функции, она наилучшим образом подходит для описания изменения полезности и ожидаемого выигрыша участников конкурентной игры. При таком подходе можно показать связь между вероятностями и функцией полезности. Другими словами, определить распределение вероятности выигрыша между конкурентами и найти, выразить вероятности выигрыша через коэффициенты функции полезности, формула 5. Аналогично можно выразить вероятности в случае, когда функция полезности имеет другой вид, например в виде логарифмической функции для этого случая вычисления проводятся аналогично формулам 4-5 при подстановке вместо выигрыша v соответствующего выражения функции полезности.

