Введение
Функционирование широкого класса предприятий ОПК заключается в поэтапном формировании и выполнении портфеля заказов. Управление его формированием связано с необходимостью принятия в близком к реальному масштабу времени решений по включению или не включению поступающих заказов в формируемый портфель. Указанные решения должны обеспечить максимально возможную рентабельность использования оборудования и других ресурсов предприятия за установленный период времени. Их обоснование осуществляется в условиях неопределенности. Неопределенность состоит в том, что виды и количество заказов, поступающих на предприятие на каждом этапе его функционирования, а также достигаемый от использования имеющихся ресурсов эффект (доход предприятия) за весь установленный период функционирования являются случайными. Принимаемые же решения должны обеспечить максимально возможный эффект [1].
Для максимизации эффекта функционирования предприятия при обосновании решений целесообразно исходить из принципа оптимальной адаптации. Его сущность состоит в том, что соответствующие решения должны быть максимально инвариантными по отношению к недетерминированным и неуправляемым условиям функционирования рассматриваемого предприятия и при этом наиболее полно использовать возможности, заложенные в детерминированных и надежно управляемых параметрах протекающего в нем производственного процесса. Практическая реализация принципа оптимальной адаптации при управлении рентабельностью функционирования предприятия ОПК не представляется возможным без автоматизации процесса формирования управленческих решений. Ключевым элементом автоматизации при этом является разработка методического подхода, реализующего указанный принцип при формировании портфеля заказов предприятия ОПК [2].
Материалы и методы исследования
С достаточной степенью общности функционирование широкого класса предприятий ОПК может быть схематически представлено в виде процесса, протекающего в некоторой системе σ, включающей (рисунок) четыре основные подсистемы – спроса, информационную, управляющую и ресурсную [3].
При этом подсистема спроса отражает внешнюю среду и формирует поток заказов, для выполнения которых могут привлекаться ресурсы рассматриваемого предприятия ОПК.
Информационная подсистема выявляет эти заказы и на каждом k-м (k=1,2,…) этапе функционирования предприятия ОПК формирует возможный набор заказов. Этот набор характеризуется вектором:
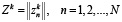 , (1)
, (1)
где 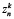 – количество выявленных к моменту времени tk начала k-го этапа заказов n-го вида, которые могут выполняться ресурсами рассматриваемого предприятия.
– количество выявленных к моменту времени tk начала k-го этапа заказов n-го вида, которые могут выполняться ресурсами рассматриваемого предприятия.
Управляющая подсистема в последовательные моменты времени t1<t2<…<T принимает решения по включению или не включению выявленных заказов в портфель заказов предприятия.
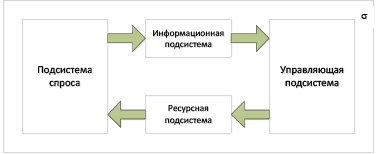
Обобщенная схема функционирования предприятия ОПК
Ресурсная подсистема обеспечивает подготовку и использование ресурсов для выполнения включенных в портфель заказов. Она характеризуется вектором
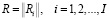 , (2)
, (2)
компоненты которого отражают количество ресурсов каждого i-го типа, которыми располагает система σ в начале функционирования.
В результате использования этих ресурсов в ходе функционирования системы σ поэтапно формируется доход предприятия. При этом цель состоит в максимизации дохода за установленный период времени T, при условии, что не включенные в портфель в ходе каждого k-го этапа заказы исключаются из рассмотрения.
Применительно к рассмотренной схематизации процесса функционирования предприятия, реализацию принципа оптимальной адаптации при распределении ресурсов целесообразно осуществлять путем использования соответствующей модели из семейства, порождаемого базовой структурой следующего вида: (3)-(7) [4].
Определить вариант распределения ресурсов:
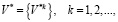 (3)
(3)
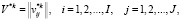 (4)
(4)
такой, что
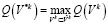 , (5)
, (5)
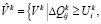
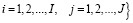 (6)
(6)
при
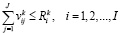 , (7)
, (7)
где
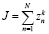 – количество заказов на k-м этапе функционирования предприятия (поступивших в момент времени tk);
– количество заказов на k-м этапе функционирования предприятия (поступивших в момент времени tk);
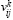 – количество расчетных единиц ресурса i-го типа, выделенное для выполнения j-го заказа на k-м этапе (в период времени (tk, tk+1)) функционирования предприятия;
– количество расчетных единиц ресурса i-го типа, выделенное для выполнения j-го заказа на k-м этапе (в период времени (tk, tk+1)) функционирования предприятия;
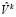 – множество вариантов распределения ресурсов, возможных на k-м этапе функционирования предприятия;
– множество вариантов распределения ресурсов, возможных на k-м этапе функционирования предприятия;
Q(Vk) – доход, получаемый предприятием на k-м этапе его функционирования (за время tk+1-tk) при реализации варианта Vk распределения имеющихся ресурсов;
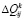 – приращение дохода при выделении расчетной единицы ресурса i-го типа для обеспечения потребностей j-го заказа на k-м этапе функционирования предприятия;
– приращение дохода при выделении расчетной единицы ресурса i-го типа для обеспечения потребностей j-го заказа на k-м этапе функционирования предприятия;
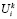 – оптимальный нижний уровень удельной эффективности для ресурсов i-го типа на k-м этапе функционирования предприятия;
– оптимальный нижний уровень удельной эффективности для ресурсов i-го типа на k-м этапе функционирования предприятия;
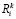 – количество ресурсов i-го типа, которыми располагает предприятие на k-м этапе функционирования;
– количество ресурсов i-го типа, которыми располагает предприятие на k-м этапе функционирования;
I – количество типов распределяемых ресурсов.
Результаты исследования и их обсуждение
В приведенной структуре модели соотношение (3) показывает, что оптимальный план распределения ресурсов формируется в виде последовательности локальных решений V*k, принимаемых в последовательные моменты времени t1<t2<…<T функционирования предприятия (системы σ).
Соотношение (4) раскрывает содержание каждого локального решения в виде матрицы, элементами которой являются, выделенные для выполнения соответствующих заказов, объемы ресурсов каждого типа.
Соотношение (5) отражает требование наиболее полного использования возможностей предприятия для получения на каждом этапе максимального дохода.
Соотношение (6) препятствует локальной оптимизации распределения ресурсов на k-м (k=1,2,…) этапе в ущерб глобальному оптимуму за весь период T функционирования предприятия ОПК. Оно представляет собой критерий для выделения из множества возможных для текущего этапа вариантов распределения ресурсов, такого подмножества, выбор из которого не противоречит достижению глобального оптимума. При этом учитывается не только сложившейся к k-му этапу ситуация, но и результаты прогнозирования ее развития в будущем. Следовательно, соотношение (6) обеспечивает адаптацию процесса функционирования предприятия к складывающимся условиям.
Соотношение (7) отражает балансные ограничения на количество распределяемых ресурсов каждого типа.
В конкретных задачах возможны и другие необходимые ограничения.
Выбор величин 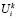 (i=1, 2,…,I) в качестве параметров адаптации обусловлен тем, что удельная эффективность использования ресурсов предприятия, являясь инвариантной характеристикой по отношению к их конкретному варианту распределения, в тоже время, достаточно просто прогнозируется и хорошо согласуется с типичной структурой моделей дискретного программирования.
(i=1, 2,…,I) в качестве параметров адаптации обусловлен тем, что удельная эффективность использования ресурсов предприятия, являясь инвариантной характеристикой по отношению к их конкретному варианту распределения, в тоже время, достаточно просто прогнозируется и хорошо согласуется с типичной структурой моделей дискретного программирования.
Конкретные модели распределения ресурсов, реализующие предлагаемый подход, получают путем явного представления зависимостей, входящих в модель (3)–(7). При этом в зависимости от вида функции Q(Vk) модель (3)–(7) может относиться к классу линейных (если Q(Vk) – линейная функция) или нелинейных (если Q(Vk) – нелинейная функция) задач целочисленного программирования.
В модели (3)–(7) возможность согласования локальных и глобального оптимумов при формировании решений по распределению ресурсов на каждом этапе функционирования предприятия ОПК обеспечивается введением вектора адаптации:
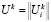 (i=1,2,…,I, k=1,2,…) (8)
(i=1,2,…,I, k=1,2,…) (8)
Конкретные методики определения его компонент определяются имеющейся информационной ситуацией. Наиболее простой при этом является ситуация, характеризуемая тем, что управляющая подсистема рассматриваемой системы (предприятия ОПК) имеет данные об общем количестве и видах заказов, которые могут поступить от подсистемы спроса. Однако не имеет данных о том, сколько и какие из них реально поступят за время T функционирования предприятия и как они будут распределены по этапам его функционирования.
Общее количество и виды возможных заказов для каждого этапа будем описывать вектором
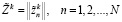 , (9)
, (9)
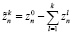 , (10)
, (10)
где 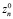 – общее количество возможных заказов n-го (n=1,2,…,N) вида, формируемых подсистемой спроса за время T;
– общее количество возможных заказов n-го (n=1,2,…,N) вида, формируемых подсистемой спроса за время T;
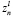 – количество возможных заказов n-го (n=1,2,…,N) вида, выявленных информационной подсистемой для выполнения на l-м этапе функционирования экономической системы.
– количество возможных заказов n-го (n=1,2,…,N) вида, выявленных информационной подсистемой для выполнения на l-м этапе функционирования экономической системы.
В такой информационной ситуации для определения компонентов вектора (8) можно воспользоваться процедурой оптимального распределения имеющихся на каждом k-м этапе ресурсов между всеми заказами, которые принципиально могут поступить на k-м и последующих этапах, то есть по заказам, определяемым вектором (9). В качестве же компонент вектора (8) принять минимальные доходы, приходящиеся на единицу ресурса i-го (i=1,2,…,I) типа в полученном распределении.
Модель оптимального распределения имеющихся на каждом k-м этапе ресурсов по заказам, определяемым вектором (9), в формализованном виде состоит в следующем.
Определить вариант распределения ресурсов:
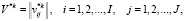 (11)
(11)
такой, что
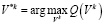 , (12)
, (12)
при
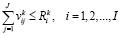 , (13)
, (13)
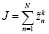 . (14)
. (14)
Если же в сложившейся информационной ситуации управляющая подсистема рассматриваемой системы имеет данные только о видах возможных заказов и интенсивностях поступления заказов каждого вида, то в основу определения компонент вектора (8) может быть положен другой подход.
Для его формализованного представления процесс формирования заказов будем представлять как совокупность потоков требований с интенсивностями, определяемыми вектором:
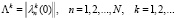 (15)
(15)
Управляющая подсистема системы σ, устанавливая пороговые значения 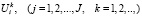 удельной эффективности применения имеющихся ресурсов каждого типа для выполнения заказов, осуществляет селекцию потоков требований в соответствии с соотношением (6). В результате формируются потоки допустимых требований, интенсивности которых определяются соотношением:
удельной эффективности применения имеющихся ресурсов каждого типа для выполнения заказов, осуществляет селекцию потоков требований в соответствии с соотношением (6). В результате формируются потоки допустимых требований, интенсивности которых определяются соотношением:
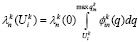
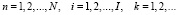 , (16)
, (16)
где 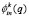 – плотность распределения эффекта использования единицы ресурса i-го типа для выполнения заказов n-го вида на рассматриваемом k-м этапе функционирования предприятия;
– плотность распределения эффекта использования единицы ресурса i-го типа для выполнения заказов n-го вида на рассматриваемом k-м этапе функционирования предприятия;
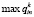 – верхняя граница эффекта использования единицы ресурса i-го типа для выполнения заказов n-го вида на рассматриваемом этапе функционирования предприятия.
– верхняя граница эффекта использования единицы ресурса i-го типа для выполнения заказов n-го вида на рассматриваемом этапе функционирования предприятия.
При формировании этих потоков параметры 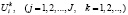 обеспечивают разрежение входного потока заказов. Если эти параметры малы, то имеющиеся ресурсы могут быть использованы и при невысоких удельных эффектах (с низкой рентабельностью). Это ведет к возрастанию риска дефицита соответствующего ресурса в будущем, когда их применение могло бы быть более целесообразным и в целом снижает рентабельность функционирования предприятия ОПК. Если же указанные параметры слишком велики, то возрастает риск неиспользования соответствующих ресурсов вследствие отсутствия подходящих заказов, что также снижает рентабельность функционирования предприятия ОПК.
обеспечивают разрежение входного потока заказов. Если эти параметры малы, то имеющиеся ресурсы могут быть использованы и при невысоких удельных эффектах (с низкой рентабельностью). Это ведет к возрастанию риска дефицита соответствующего ресурса в будущем, когда их применение могло бы быть более целесообразным и в целом снижает рентабельность функционирования предприятия ОПК. Если же указанные параметры слишком велики, то возрастает риск неиспользования соответствующих ресурсов вследствие отсутствия подходящих заказов, что также снижает рентабельность функционирования предприятия ОПК.
Задача состоит в выборе оптимальных значений параметров 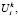
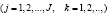 , которые бы с учетом указанных факторов риска обеспечивали максимальное значение математического ожидания эффекта применения имеющихся ресурсов.
, которые бы с учетом указанных факторов риска обеспечивали максимальное значение математического ожидания эффекта применения имеющихся ресурсов.
Если значения 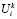 (i=1,2,…,I) на k-м шаге зафиксированы, то ожидаемая удельная эффективность применения ресурсов i-го типа для выполнения заказов на этом шаге характеризуется плотностью вероятностей
(i=1,2,…,I) на k-м шаге зафиксированы, то ожидаемая удельная эффективность применения ресурсов i-го типа для выполнения заказов на этом шаге характеризуется плотностью вероятностей
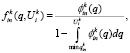
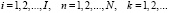 , (17)
, (17)
где 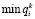 – нижняя граница величины
– нижняя граница величины 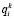 .
.
С учетом (17) математическое ожидание 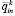 удельного эффекта применения ресурсов i-го типа для выполнения заказов n-го вида на k-м этапе функционирования предприятия определяется соотношением:
удельного эффекта применения ресурсов i-го типа для выполнения заказов n-го вида на k-м этапе функционирования предприятия определяется соотношением:
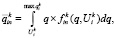
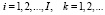 (18)
(18)
Если при этом ресурсы в процессе функционирования предприятия не возобновляются, то ожидаемый полный эффект от их использования на k-м этапе с учетом (17) можно рассчитать по формуле:
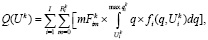
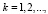 (19)
(19)
где m – количество единиц ресурса i-го типа, использованных на k-м этапе функционирования предприятия для выполнения заказов;
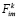 – вероятность использования для выполнения заказов на k-м этапе функционирования предприятия m единиц ресурса i-го типа.
– вероятность использования для выполнения заказов на k-м этапе функционирования предприятия m единиц ресурса i-го типа.
Для возобновляемых ресурсов предприятия получаемый в результате их использования эффект определяется соотношением
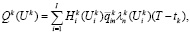
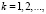 (20)
(20)
где 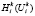 – вероятность использования по назначению условной единицы ресурса i-го типа.
– вероятность использования по назначению условной единицы ресурса i-го типа.
Вектор (8) должен обеспечивать максимальную эффективность использования выделенных ресурсов. Поэтому определение его оптимальных компонент 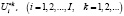 может быть сведено к решению следующей экстремальной задачи
может быть сведено к решению следующей экстремальной задачи
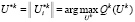 . (21)
. (21)
Дальнейшая конкретизация представленного подхода состоит в конструктивном представлении целевой функции Q(Vk) и функций 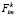 ,
, 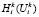 ,
, 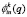 .
.
Выводы
В целом рассмотренный методический подход позволяет при формировании портфеля заказов предприятия учесть такие существенные черты функционирования предприятий ОПК, как динамичность и неопределенность ситуации, и в тоже время использовать для выработки решений относительно простой аппарат статической оптимизации. Процесс управления формированием портфеля заказов предприятия приобретает при этом адаптивный характер.
Указанные обстоятельства обусловливают целесообразность применения предложенного подхода при построении автоматизированных систем поддержки принятия решений в интересах формировании портфелей заказов предприятий ОПК, функционирующих в характерных для экономических систем условиях неопределенности.

