Введение
Поскольку экономические субъекты сферы ЖКХ заняты ведением производственно-хозяйственной деятельности, то представляется вполне логичным предположить, что при ее осуществлении ни один субъект не будет принимать решений, последствием которых может стать получение убытка [1, c. 301]. Напротив, основной целью деятельности каждого экономического субъекта в условиях рынка является обеспечение ее доходности. Только получение достаточного дохода позволяет экономическим субъектам нормально функционировать и развиваться. Для этого они должны обоснованно делать выбор и принимать те или иные многокритериальные решения при осуществлении своей деятельности в условиях вероятностной неопределенности. Важную роль в решении этой проблемы может сыграть использование методов экономико-математического моделирования.
Основная цель данного исследования заключается в обосновании использования существующих методов экономико-математического моделирования для разработки моделей выбора и принятия решений экономическими субъектами сферы ЖКХ с учетом факторов вероятностной неопределенности на основе задания их предпочтений на множестве допустимых вероятностных распределений случайного набора решений при симметричных и несимметричных распределениях.
Материал и методы исследования
Инструментарий формирования модели выбора и принятия решений в условиях вероятностной неопределенности может основываться на определении предпочтений экономического субъекта на множестве допустимых вероятностных распределений случайного набора решений. Предположим, что каждое решение r в некотором множестве R = {R} допустимых вероятностных распределений является случайной величиной. Далее будем полагать, что все описания случайных величин можно практически без изменений применять и к случайным векторам. Тогда проблему выбора и принятия решения для случайных величин можно представить как проблему формирования векторного критерия l(r,y) = (l1(r,y), …, ln(r,y)), где r ∈ R – набор допустимых решений, y ∈ Y – факторы неопределенности. При этом, если считать каждый фактор неопределенности y – случайным параметром на множестве Y, то и векторный критерий l(r,y) также можно считать случайной величиной.
В последующих рассуждениях будем исходить из того, что допустимое решение r как случайная величина равнозначно некоторому случайному доходу d, а проблема выбора и принятия решения экономическим субъектом заключается в максимизации этого дохода. Для этого необходимо, чтобы для экономического субъекта на множестве R ={R} допустимых вероятностных распределений были заданы предпочтения, то есть определено понятие «распределение R «лучше», чем распределение K». Обозначим отношение предпочтения через выражение R > K. Отношение предпочтения можно вычислить в том случае, если существует функционал F, определенный на множестве R, такой, что R > K ⇔ F(R) ≥ F(K).
Функционал F будем называть индикатором предпочтения, поскольку его смысл заключается в том, что для исчислимых отношений предпочтения каждому распределению можно поставить в соответствие некоторое число, с тем, чтобы в дальнейшем сравнивать эти распределения через сравнение указанных чисел. В таком случае предпочтения на множестве распределений будут заданы естественным порядком на множестве действительных чисел [2, c. 68].
Если индикатор предпочтения существует, то всякая строго возрастающая функция от него даст тот же самый индикатор предпочтения, поскольку само предпочтение осталось прежним, а меняется только масштаб шкалы оценки распределений. При этом будет верным и обратное утверждение: если имеются два индикатора одного и того же предпочтения U и V, то существует строго возрастающая функция q, такая, что V = q(U). Это значит, что такого рода индикаторы предпочтения всегда определены с точностью до строго монотонного преобразования.
Необходимым и достаточным условием того, что некоторое отношение может быть задано индикатором является ограничение характеристик распределения случайной величины только первыми двумя параметрами, а именно: ее математическим ожиданием m и дисперсией σ2. В том случае, если нас интересует распределение случайного дохода d неких экономических субъектов, то будет вполне естественным выбрать распределение с большим математическим ожиданием m, а в случае равенства математических ожиданий – сделать выбор в пользу распределения с меньшей дисперсией σ2. Однако на практике не существует числовых функций для того, чтобы задать такого рода отношение предпочтения невозможно никакой. Чтобы выйти из этого положения, формализуем ряд требований для определения предпочтений экономического субъекта на множестве допустимых вероятностных распределений случайного набора решений.
Предположим, что dx0 – распределение, сосредоточенное в точке x0. В этом случае мы имеем дело с вырожденным распределением, поскольку рассматриваемая нами случайная величина на самом деле детерминированная и может принимать только одно значение x0. Однако это обстоятельство не мешает нам формально включить эту детерминированную величину в совокупность случайных величин. Теперь, если предположить, что случайная величина описывает некоторый доход экономического субъекта, то условие x0 ≥ x1 ⇒ dx0 > dx1 означает, что с увеличением дохода улучшается распределение. В нашем случае функции распределения dx0 и dx1 связаны соотношением dx0(x) ≤ dx1(x) для всех x. В дальнейшем воспользуемся утверждением о том, что «распределение R лучше распределения K» (R > K) означало, то есть:
R(x) ≤ K(x) (1)
для всех x и всех распределений, включая и вырожденные.
Условие (1) будем считать условием стохастического доминирования. В практической деятельности экономических субъектов оно отражает их стремление к увеличению дохода d. Для того, чтобы рассмотреть предположения, связанные со стремлением к «стабильности» дохода, введем ряд дополнительных понятий. Так, будем считать, что распределение R симметрично с центром симметрии m, если для всех x>0 выполняется равенство:
R(m–x)= 1 – R(m+x+0). (2)
Для случайной величины дохода d с распределением R это условие означает, что имеет место следующее соотношение между вероятностями:
P{(d – m) > x} = P{(d – m) < – x}, (3)
то есть, вероятности отклонений случайной величины дохода d от центра симметрии в любую сторону будут равны между собой.
Сделанные выше предположения позволяют формализовать условие «стабильности» дохода экономического субъекта в сфере ЖКХ следующим образом.
Пусть R и K – симметричные распределения с общим центром симметрии m и пусть при x ≤ m имеет место условие:
R(x) ≤ K(x) ⇒ R > K. (4)
На практике условие (4) означает, что если существуют случайная величина ξ с распределением R, случайная величина k с распределением K, и эти распределения симметричны с общим центром симметрии m, то при всех x>0 будет выполняться условие:
P{|d – m| > x} ≤ P{|k – m| > x}. (5)
Другими словами, если R – нормальное распределение со средним m и дисперсией σ12 , а K – нормальное распределение с тем же средним m и дисперсией σ22 > σ12, то условием стремления к стабильности будет предпочтение распределения R распределению K. Таким образом, с требованием стабильности согласуются условия (4) и (5) [3, c. 116]. Это значит, что проблема выбора и принятия экономическим субъектом решений для получения некоторого дохода в условиях вероятностной неопределенности при симметричных распределениях случайных величин имеет решение.
Однако, практика показывает, что это достаточно простой случай. Более сложным случаем является выбор и принятие экономическим субъектом сферы ЖКХ решений для получения некоторого дохода в условиях вероятностной неопределенности при несимметричных распределениях или распределениях с разными центрами симметрии. Действительно, если требуется сравнить два нормальных распределения с параметрами математического ожидания и дисперсии следующего вида, соответственно, (m1, σ12) и (m2, σ22), то экономическому субъекту необходимо каким-то образом соотносить между собой стремление увеличить математическое ожидание m (повысить доход) и уменьшить дисперсию σ2 (повысить стабильность).
Эта проблема может быть решена через определение индикатора предпочтения на множестве допустимых вероятностных распределений случайного набора решений и функцию полезности. При этом в качестве индикатора предпочтения на множестве вероятностных распределений целесообразно выбрать среднее значение функции полезности [4, c. 91]. Таким образом, получим следующее выражение:
F(R) = ∫g(d)dR(d) , (6)
где g(d) – функция полезности.
Выражение (6) обладает таким свойством, что для любых двух чисел α≥0, β≥0, α+β=1 всегда будет существовать следующее равенство:
F(aR + bK) = aF(R) + bF(K). (7)
В практической деятельности экономического субъекта выражение (7) можно трактовать следующим образом. Если экономический субъект выбирает два варианта получения дохода – 1) с вероятностью a и с распределением R, и 2) с вероятностью b и с распределением K, то итоговое распределение дохода для него будет равнозначно смешанному распределению (aR + bK).
Если величину дохода d считать случайной величиной, то можно утверждать, что экономический субъект, не стремится к принятию рискованных решений, при условии
g(md) > mg(d), (8)
и склонен к риску в случае
g(md) < mg(d), (9)
где m – символ математического ожидания, а g(d) – функция полезности.
Другими словами, не склонный к принятию рискованных решений экономический субъект отдаст предпочтение решение, для которого полезность среднего дохода будет превышать среднюю полезность дохода. И наоборот, склонный к принятию рискованных решений экономический субъект, будет стремиться к принятию противоположного решения.
На первый взгляд кажется, что применение индикатора предпочтения (6) выглядит достаточно обоснованным при сравнении между собой несимметричных распределений или распределений с разными центрами симметрии. Однако он не всегда оказывается приемлемым, поскольку представляет собой линейный функционал.
Для выхода из такого рода ситуаций целесообразно использовать в качестве индикатора предпочтения нелинейные функционалы. Рассмотрим один из подходов к построению таких функционалов. Введем функцию «сравнительной полезности» h(u,v), которая показывает, насколько доход u представляется для экономического субъекта «лучше», чем доход v. В этом случае будем считать, что при u ≥ v h(u,v) ≥ 0, а при u ≤ v h(u,v) ≤ 0.
Допустим, что случайная величина дохода d имеет распределение R. Тогда среднюю сравнительную полезность случайного дохода экономического субъекта d по отношению к его детерминированному доходу v можно выразить следующим образом:
g(v) = mh(d,v) = ∫h(x,v)dR(x) .
Далее будем использовать как индикатор предпочтения F(R) корень уравнения:
g(v) = 0. (10)
Выражение (5) представляет собой детерминированный доход v экономического субъекта, у которого сравнительная полезность по отношению к случайному доходу d в среднем всегда будет нулевой. Другими словами, детерминированный доход v в среднем эквивалентен случайному доходу экономического субъекта d.
Если предположить, что
h(u,v) = ω(u)(f(u) – f(v)),
где ω(u) – некоторая весовая функция, то решение уравнения (6) будет иметь следующий вид:
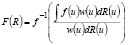, (11)
где f –1 обратная функция.
После проведенной формализации все приведенные выше обоснования выражений «доход d1 лучше дохода d2», можно применить к векторным критериям, поскольку уже определены условия, при которых «вектор l1 лучше вектора l2». Поэтому все соображения относительно построения индикатора предпочтения в условиях вероятностной неопределенности можно перенести и на случай векторного критерия l. При этом речь уже будет идти о распределении случайного вектора l и соответствующей многомерной функции полезности.
Результаты исследования и их обсуждение
В результате проведенных исследований были обоснованы возможности использования экономическими субъектами сферы ЖКХ существующего инструментария для формирования модели выбора и принятия решений с учетом факторов вероятностной неопределенности на основе определения предпочтений экономического субъекта на множестве допустимых вероятностных распределений случайного набора решений при симметричных и несимметричных распределениях.
Заключение
Разработанные модели выбора и принятия решений с учетом факторов вероятностной неопределенности на основе определения предпочтений экономического субъекта на множестве допустимых вероятностных распределений случайного набора решений при симметричных и несимметричных распределениях могут найти практическое применение в повседневной деятельности экономических субъектов сферы ЖКХ.
Благодарности
Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований, проект №17-06-00015а «Формирование методологических основ комплексной модернизации и инновационного развития сферы жилищно-коммунального хозяйства: концептуальные обоснования, механизмы, модели, технологии, инструментарий».