Научный журнал

Вестник Алтайской академии экономики и права

Print ISSN 1818-4057

Online ISSN 2226-3977

Перечень ВАК

Введение

В ранних работах одного из авторов и его научного руководителя проф. Халикова М.А. (конкретно, [1, 2]) рассматривалась проблематика оценки эффективности собственного и заемного финансирования и анализа структуры капитала операционного сегмента корпорации, имеющий доступ к ресурсам внутреннего и внешнего финансовых рынков. Авторами обоснован тезис о преимуществах смешенного финансирования предприятий корпоративного бизнеса в условиях конкурентных товарных и финансовых рынков, а также сформулирована проблема разработки экономико-математического инструментария моделей и методов выбора оптимальной структуры капитала, финансирующего затраты производственной деятельности хозяйствующих субъектов с учетом рисков их внешней и внутренней сред. В частности, одной из сформулированных задач ставилась разработка и адаптация моделей и численных методов выбора оптимальной по критерию затрат на обслуживание собственного и заемного капитала структуры пассивов рабочего капитала производственной корпорации, функционирующей в реальном секторе экономики. Решению этой целевой задачи и посвящена настоящая работа.

Материалы и методы исследования

«Отправной» работой по тематике настоящего исследования является статья М.А. Горского и М.А. Халикова [13], в которой рассматриваются постановка задачи, математическая модель и численные алгоритмы выбора оптимального размера операционного (производственного) сегмента предприятия в условиях детерминированных параметров макроэкономической среды. Эта работа проведена в рамках так называемого «неоклассического» подхода, основанного на концепции производственной функции и аппарате оценки эффективности и риска производственной деятельности корпорации, представленного в работах: А.М. Антиколь, М.А. Халикова [3], М.А. Бендикова и И.Э. Фролова [5], М.А. Горского [6,7,8], В.А. Колемаева [11], Б. Коласса [10], М. Круи [12], М.А. Халикова, А.И. Дерябиной, Д.А. Лях [14], О.Е. Хрусталева [18], М.А. Горского и Е.М. Решульской [19], Ф. Турино [21] и П. Самуэльсона [22].

Как следует из цели работы, ее основной направленностью является выбор и обоснование критерия оптимальности рабочего капитала производственной корпорации, что потребовало привлечения источников по этой и более широкой проблематике оценки эффективности и риска источников финансирования и оптимального управления ее операционной сферой в условиях турбулентных товарных и финансовых рынков. Эта проблематика поднимается в работах Д.А. Безухова [4], М.А. Никифоровой и М.А. Халикова [16, 17], М.А. Халикова, Е.С. Кулинченко, А.А. Струковой [15].

Используемый авторами математический инструментарий методов и численных алгоритмов задач нелинейной (в данном случае, выпуклой), непрерывной и дискретной оптимизации заимствован из работ М.А. Горского [6,7,8], М.А. Горского и И.И. Епифанова Горского [9], М.А. Халикова, М.А. Горского и Д, А. Максимова [20].

В расчетах по приведенным в работе моделям авторы использовали статистическую базу и данные о капитале и рыночной деятельности конкретного предприятия строительной отрасли, базирующегося в Московском регионе.

Результаты исследования и их обсуждения

Рассмотрим постановку задачи и формальную модель выбора структуры рабочего капитала операционной (производственной) сферы предприятия, минимизирующей затраты на его обслуживание.

Пусть с(у) – минимальные полные затраты на производство продукции в операционном сегменте предприятия объемом у (в натуральных ед. или ед. стоимости), которые должны быть покрыты из собственных и заемных источников финансирования.

Напомним, ссылаясь на монографию М.А. Халикова и А.М. Антиколь [3], на один из возможных способов оценки величины с(у) в рамках неоклассической теории эффективности производства.

Если 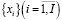– набор используемых в производственном процессе постоянных и переменных активов, приобретаемых на открытых, конкурентных рынках по ценам 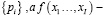производственная функция предприятия, в аналитической форме устанавливающая зависимость объема производства от затрат активов группы {xi}, то значение с(у) для объема производства у может быть получено как решение следующей задачи нелинейного программирования:

с(у) =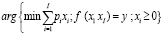.(1)

Составим функцию Лагранжа модели (1):

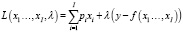(2)

и с использованием следующей системы уравнений найдем оптимальный для объема производства у набор 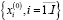потребляемых активов:

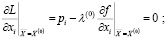
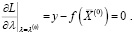(3)

Учитывая, что

,

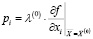запишем выражение для с(y):

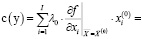
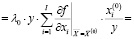
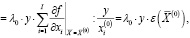(4)

где 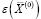– суммарная эластичность производственной функции в точке оптимального для производства объемом у набора постоянных и переменных активов.

Введем следующие обозначения для используемых далее переменных и параметров:

β – коэффициент автономии рабочего капитала

(β = CK / (CK + ЗК),

где СК – собственный;

3К – заемный капитал в пассивах рабочего капитала);

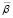– нижнее (предельное) значение коэффициента автономии, соответствующее планируемому собственниками и менеджментом уровню риска потери финансовой устойчивости производственной сферы;

re – цена собственного капитала, рассчитанная, например, по модифицированной Р. Хамадой модели САРМ [9,21] и отражающая альтернативную доходность капитала акционеров, размещенного в ценные бумаги с аналогичным инвестициям в рабочий капитал принадлежащего им предприятия уровнем риска (ниже предполагается, что цена собственного капитала – величина постоянная на рассматриваемом временном промежутке, что, конечно, не так: с ростом риска структуры рабочего капитала (ростом доли заемного финансирования) растут и риски акционеров, рассчитывающих на их покрытие за счет более высокой доходности);

r3 = r3(β) – цена (ставка) заемного финансирования, задаваемая зависимостью ставки (в общем случае, нелинейной) в аналитической или табличной формах от коэффициента автономии;

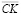– максимальный объем собственного финансирования затрат операционного сегмента предприятия в рассматриваемом временном промежутке.

Учитывая, что

β = CK / с(у) (5)

и принимая во внимание формулу WACC средневзвешенной стоимости капитала [1], запишем формальную модель выбора оптимальной структуры рабочего капитала операционной сферы предприятия для покрытия производственных затрат объемом с(у) в расчете на объем производства у:

ZK(β) = с(у) ∙ (re ∙ β + (1– β) ∙ r3(β)) → min; (6)

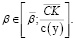(7)

Отметим, что из условия (7) следует, что, планируя максимальный объем 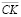выделяемых на финансирование затрат операционного сегмента собственных средств, необходимо учитывать ограничение:

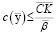(8)

на предельный для порогового значения 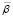коэффициента автономии объем покрываемых затрат, соответствующих максимально возможному для этих условий значению 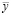объема выпускаемой продукции. Отсюда следует, что y ≤ y.

Отметим также, что в критерии (6) с(у) – константа, рассчитываемая до момента принятия решения о структуре рабочего капитала, а сомножитель 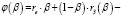дифференцируемая функция, стационарная точка β0 (точки) которой удовлетворяют соотношению:

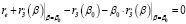(9)

или

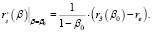(9')

Отметим, что на интервале 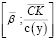существует хотя бы одна стационарная точка функции φ(β), так как характер ее монотонности на нем не детерминирован: с ростом коэффициента автономии растет нагрузка на собственный капитал, снижается нагрузка на заемный капитал (однако, не пропорционально) и наоборот.

Определим знак второй производной функции φ"(β) в точке β0 и определим условие, при котором полученное решение – точка минимума:

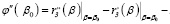
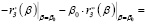
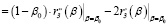(10)

Учитывая, что β0 < 1 (заемное финансирование присутствует), запишем требуемое условие:

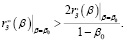(11)

Если в неравенстве (11) – противоположный знак, то стационарная точка – точка максимума, а, значит, оптимальная по критерию минимума затрат на обслуживание привлекаемого в пассивы рабочего капитала его структура соответствует предельным значениям коэффициента автономии, установленным ограничением (7), что предполагает сравнение значений критерия (6) для β, равных β и .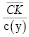

Таким образом, можно утверждать, что принадлежность точки β0, характеризующей оптимальное с позиции затрат на обслуживание капитала операционного сегмента предприятия значение коэффициента автономии собственного капитала, интервалу возможных значений в границах неравенства (7) зависит от характера поведения функции rз(β), т.е. наличие или отсутствие в интервале 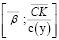точки оптимума структуры рабочего капитала определяется динамикой зависимости ставки заемного кредитования от его доли в капитале.

Рассмотрим этот аспект на конкретном примере. Для построения аналитической зависимости «риск структуры рабочего капитала – процентная ставка по кредиту» используем интерполяционный многочлен Лагранжа степени n, построенный с использованием известных значений пары «рычаг капитала «li» – стоимость заемного финансирования» :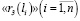

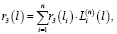(12)

где n-степень многочлена Лагранжа; i – индекс наблюдаемой точки, описывающей моделируемую зависимость; 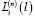– лагранжевый коэффициент (13):

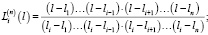
Напомним, что рычаг l капитала – отношение заемных средства к собственным связан с коэффициентом β автономии отношением:

l = (1–β) / β. (14)

Принципы построения интерполяционного многочлена Лагранжа достаточно подробно представлены в монографии Н.С. Бахвалова, Н.П. Жидкова и Г.М. Кобелькова (ссылка представлена в работе Колемаева В.А. [11], в которой доказан факт о единственности полинома (12) степени n–1 (где n – число наблюдаемых пар {li, r3(li)}. Также в цитируемой работе предложена процедура повышения точности аппроксимации rз(l) полиномом (12), включающая следующие дополнительные шаги:

- расширение множества наблюдаемых пар для моделируемой зависимости и построение интерполяционных многочленов для различных значений n;

- аудит построенной зависимости на основе контрольных расчетов в новых (не использованных ранее) узловых точках;

- оценка погрешности интерполяционного полинома и выбор узлов, обеспечивающих наименьшую погрешность.

Выбор оптимальной структуры рабочего капитала операционной сферы предприятия проведем для строительной компании ХХХ (название компании скрыто по соображениям соблюдения конфиденциальной для нее информации), занимающейся строительством многоэтажной жилой недвижимости эконом-класса в Московской области.

Для построения полинома (12) используем данные Банка России о средневзвешенных ставках по рублевым кредитам нефинансовым организациям сроком до года (таблица 1) и данные пассива рабочего капитала компании ХХХ в разрезе собственных средств (таблица 2).

Таблица 1

Средневзвешенная ставка по рублевым кредитам нефинансовым организациям

Таблица 2

Заемные и собственные средства строительной компании ХХХ

На исследуемом временном интервале (2016 – 2021 г.г.) все используемые в расчетах показатели являются среднегодовыми.

Получен следующий полином (12) четвертой степени:

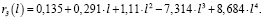(15)

или

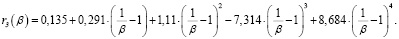(16)

Из (16) следует:

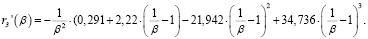(17)

Используя выражение (17) для 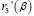, составим (в соответствии с (9')) уравнение для нахождения стационарной точки β0:

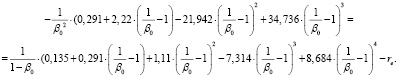(18)

или

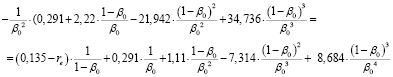(18')

С использованием уравнения (18) определим оптимальную структуру и стоимость рабочего капитала исследуемой компании для различных значений доходности собственного финансирования ее производственной сферы (таблица3).

Таблица 3

Оптимальная структура и стоимость рабочего капитала компании ХХХ.

Проведенные эмпирические расчеты для компании строительной отрасли позволяют сделать следующие выводы:

- высокая фондоемкость и значительные полные затраты производственной деятельности не позволяют в полной мере использовать в строительной отрасли эффект «рычага капитала», существенно сократить затраты на заемный капитал и снизить средневзвешенную стоимость рабочего капитала за счет повышения риска его структуры;

- доказан обоснованный в работах Горского М.А. и Халикова М.А. [9,13,15,17] факт возможности конструктивного определения оптимальной структуры капитала корпорации, зависящей от параметров финансовых рынков и проводимой политики собственного финансирования рыночной деятельности;

- в оценках ставок заемного финансирования производственной сферы корпорации наряду с риском структуры капитала необходимо учитывать и другие параметры ее внешней и внутренней сред, что позволит более точно указать их прогнозные уровни и далее скорректировать принимаемые на их основе финансовые решения.

Заключение

В статье на содержательном уровне рассмотрена постановка, представлены модель и численные алгоритмы выбора оптимальной структуры рабочего капитала корпорации, функционирующей в реальном секторе экономики. Обоснован критерий оптимальности структуры капитала, основанный на показателе риска потери финансовой устойчивости. Приведены условия оптимальности структуры капитала и представлен соответствующий численный пример. Можно считать, что эта публикация логически завершает цикл теоретических исследований проф. Халикова М.А. и его учеников в направлении моделирования оптимальной структуры капитала производственной корпорации с учётом неопределенности и риска ее внешней и внутренней сред, выбор которой предполагается осуществлять как в статичном, так и динамическом вариантах.

Основные усилия в дальнейших исследованиях авторы планируют направить на совершенствование теоретической базы и практических алгоритмов оценок ставок собственного и заемного финансирования рыночной деятельности хозяйствующих субъектов акционерной формы собственности и госкорпораций в условиях ограниченного и неограниченного доступа к источникам капитала.