Введение
В процессе постоянного совершенствования информационных технологий возрастает потребность в разработке автоматизированных средств оперативной поддержки решений при анализе экономико-математических задач. Одним из важных классов таких задач является задача оценки эффективности инвестиционных проектов [1], которая, в свете необходимости развития малого и среднего предпринимательства, в Российской Федерации, принимает особую актуальность. Решение такой задачи требует применения моделей и методов, позволяющих, с одной стороны, c достаточной скоростью, а с другой, – с высоким уровнем достоверности автоматизировано оценивать эффективность инвестиционных проектов (ИП), например, с помощью наглядных графоаналитических методов и программных комплексов. Следует отметить недостаточное количество математических моделей ИП, в которых выявлялся бы их жизненный цикл, подразумевающий наличие периодов окупаемости, роста, достижения максимальных значений и возможного последующего спада некоторого показателя эффективности ИП, например, чистой приведенной стоимости (net present value, NPV). Спад NPV, как динамического показателя, зависящего, в частности, от прибыли инвестиционного проекта (которая может, в течение горизонта планирования, может становиться и отрицательной величиной за счет превышения потоков затрат над порожденными инвестицией потоками выгод).
Целью данной работы является изучение вопроса применения одного инструментально-аналитического подхода к оперативной оценке экономической эффективности инвестиционных проектов с возможностью выявления их жизненного цикла. Указанный подход заключается в использовании комплекса инструментально-аналитических средств, включающего одноформульную математическую модель оценки экономической эффективности инвестиционных проектов, алгоритма ее численного анализа и самого численного анализа с помощью автоматизированного программного продукта, ориентированного на оперативный, многоаспектный анализ и автоматизированную поддержку принимаемых инвестиционных решений в ситуационно-аналитических центрах [2].
Материалы и методы исследования
В статье [3] описана работа графоаналитического комплекса [4] (далее графического анализатора, графоанализатора), позволяющего одновременно осуществлять многопараметрический анализ функций с несколькими параметрами, в том числе общими для выбранных функций, в режиме реального времени, со скоростью до нескольких десятков перебираемых значений параметра в секунду. К основным отличительным свойствам комплекса относятся возможности автоматического распознавания переменных и использования практически не ограниченного количества параметров, их изменение в ручном и автоматическом режимах. Кроме того, возможности данного программного продукта позволяют находить критические точки функций (корни, экстремумы, перегибы), точки пересечения нескольких функций, получать уравнения касательных, вычислять определенные интегралы, графически анализировать системы уравнений и неравенств с общими параметрами на общем графическом поле, решать другие полезные для математического анализа функций задачи. Пакет также обладает ключевым преимуществом (характерным и для других графических пакетов [5,6]), заключающимся в возможности приближенного определения корней алгебраических соотношений, аналитическое получение которых излишне затратно или даже невозможно (например, когда необходимо найти корни полинома степени выше 2-й или в решаемом соотношении одновременно присутствуют функции разных классов – степенная, показательная, логарифмическая, тригонометрическая и т.п.). Существенными возможностями указанного пакета является оперативная визуализация и динамический анализ изучаемых объектов и процессов путем построения и многопараметрического исследования функций с использованием простого и интуитивно понятного интерфейса, доступного для освоения обучающимися образовательных организаций основного, профессионального и высшего образования [7-9]. Иначе говоря, пакет [4] отвечает уровню и классу задач, в частности, требующих решения при оценке инвестиционных проектов.
Хорошо проверенным, разноплановым методом анализа инвестиционных проектов является метод расчета его чистой приведенной стоимости, основанный на оценке объема абсолютного значения сальдо стратегических финансовых потоков (потоки прибыли, как сальдо доходных и расходных потоков, стоимости имущественного комплекса и др.) и вложенных в проект инвестиций [1,10-14]. В работе [2] с помощью пакета [4] проведен параметрический анализ ИП, в котором NPV рассчитывается по формуле:
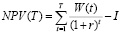, (1)
описывающей ИП с одноразовой инвестицией I в начальный момент времени проекта t=0 и порождаемыми ею производством и продажей продукции, приносящими прибыль W(t)=const в моменты времени t=1,…,T, дисконтируемую по ставке r>0. Формула (1) позволяет определять добавленную стоимость и период окупаемости инвестиционного проекта, если ее рассматривать в виде NPV(Т), а также внутреннюю норму доходности этого же проекта, в случае ее представления в виде NPV(r). С помощью параметрического графоанализатора указанная функция может быть исследована параметрически по любому из входящих в нее параметров. Следует отметить, что характерной, существенной для нас, особенностью функции (1) является ее неубывание по параметру Т, так как при W(t)≥0 результат формируется нарастающим неотрицательным итогом, что не позволяет выявлять жизненный цикл инвестиционного проекта, подразумевающий наличие периодов окупаемости, роста, достижения максимальных значений и последующего спада эффективности. Вместе с тем, возникновение указанного спада возможно при отрицательном сальдо потоков, в результате превышения расходов ИП над доходами.
Рассмотрим случай, когда в (1) W(t)≠const, например, [10]:
W(t) = [Qt(Pt – Vt) – F – Amt] (1 – αw), (2)
где Qt – объём произведенной продукции, Pt – цена единицы продукции, Vt, F – соответственно условно-переменные (на единицу продукции) и условно-постоянные затраты, Аmt – амортизация, αw – ставка налога на прибыль. Следует отметить, что именно потоки Vt и Amt, вообще говоря, могут превысить положительный поток Qt‧Pt, в случае отсутствия дополнительных инвестиций на горизонте планирования ИП. В частности, численные расчеты, представленные, например, в [15], в оптимизационных моделях инвестиционных проектов которых использованы формулы, аналогичные (2), показывают наличие максимумов зависимостей NPV(Т). Анализ соответствующих расчетов, в частности, показывает влияние потоков VT и АmT на формирование отрицательного сальдо потоков, предопределяющих возникновение убывающего участка NPV(Т), то есть классического жизненного цикла ИП.
Содержательная постановка задачи оценки эффективности ИП подразумевает влияние на эту оценку различных экономических факторов, одним из существенных среди которых является амортизация основных производственных фондов (ОПФ). Рассмотрим следующую разновидность формулы (1):
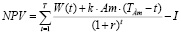(3)
где Am – поток амортизационных отчислений, TАm – срок службы (полезного использования) ОПФ. В формуле (3) выражение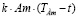 
можно содержательно трактовать следующим образом: при t<TАm величина амортизации учитывается в доходных потоках ИП, как стоимостной измеритель остаточной стоимости имущества с коэффициентом k, трактуемым, как норма амортизации, а при t>TАm величина амортизации уменьшает доходные потоки ИП за счет увеличения издержек на возмещение износа (ремонт, восстановление, обновление программного обеспечения и пр.) ОПФ, причем, чем далее от значения срока TАm полезного использования, чем с большей скоростью, что и отражается в обратно пропорциональной линейной зависимости потоков от времени.
Результаты исследования и их обсуждение
Отметим, что вид формулы (3) принципиально меняет класс рассматриваемого функционального ряда (1), превращая его из геометрической прогрессии (при W(t)=const) в более сложный ряд за счет наличия суммы вида
,
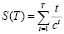где с=1+r>1. Для вычисления указанной суммы преобразуем S(Т):
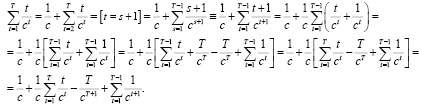
Учитывая, что сумма во втором слагаемом последнего выражения совпадает с искомой, а его четвертое слагаемое является геометрической прогрессией с первым членом 1/с2 и знаменателем 1/с, получим
,
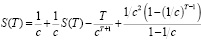а c учетом того, что с>1,
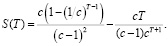
Вычисляя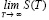 
, найдем сумму S бесконечного ряда, соответствующего искомому: 
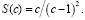При с=1+r, очевидно,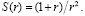 
Исследуем полученную функциональную зависимость S(Т) с помощью параметрического графоанализатора [4]. На рисунках 1 и 2 представлены функция S(Т) и ее производная S’(Т) по осям T–S в масштабах 1×10 и 1×1 соответственно.
Как можно видеть из рисунка 1, функция S(Т) монотонно возрастает на положительной части оси Т, имеет перегиб и асимптотически приближается к значению (1+r)/r2 при Т→∞, а производная S’(Т) имеет экстремум, точку перегиба и асимптотическое приближение к нулю при Т→∞. Причем критическая точка S’(Т) визуально значительно легче определяется средствами пакета [4] по рисунку 2 в масштабе 1×1, чем по рисунку 1. Тем самым, анализ рисунков 1,2 позволяет рассчитывать на наличие точки экстремума и в формуле (3), для функции NPV(T). Проверим данную гипотезу также с помощью графоанализатора [4] при следующих значениях параметров: I=20; r=0,3; W=7 при варьировании показателя TАm. Результаты проведенных расчетов представлены на рис.3.
Как видно из рисунка 3, зависимости NPV(T) действительно имеют выраженную точку экстремума Тэкстр, причем, с ростом TАm, значение NPV также растет, что соответствует экономическому смыслу данного параметра, как одного из параметров, существенно определяющих экономическую устойчивость проекта. Кроме того, рисунок 3 иллюстрирует снижение периода окупаемости инвестиционного проекта за счет более высокой нормы амортизации.
Представленные зависимости, в первом приближении, подтверждают выдвинутую гипотезу о возможности выявления жизненного цикла инвестиционного проекта.
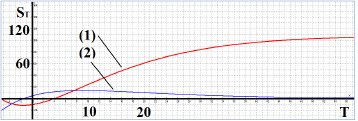
Рис. 1. Зависимости S(Т) – (1) и S’(Т) – (2) в масштабе 1×10
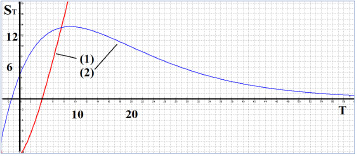
Рис. 2. Зависимости S(Т) – (1) и S’(Т) – (2) в масштабе 1×1
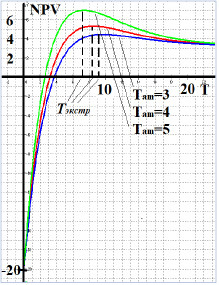
Рисунок 3. Зависимости NPV(T) при варьировании параметра TАm
Это было подтверждено в проведенных вычислительных экспериментах при варьировании других, содержательно важных экономических характеристик – прибыли, объема инвестиций, нормы амортизации, ставки дисконтирования.
Заключение
Приведенные результаты свидетельствуют о возможности выявления жизненного цикла инвестиционных проектов в одноформульных многопараметрических зависимостях, имеющих содержательный экономический смысл. Это может позволить осуществлять более качественный анализ инвестиционных проектов, включающий, например, определение моментов времени, как точек максимума исследуемых зависимостей на горизонте планирования, при которых целесообразно реинвестировать в них. Такой анализ может быть успешно применен в условиях семинаров, мобильных заседаний экспертных групп, ситуационных центров социально-экономического анализа [13], за счет наглядности и скорости производимых расчетов, простоты использования описанных инструментов. Данный подход, по сути, является реализацией системно-аналитической процедуры оценки эффективности инвестиционных проектов, так как включает математическую модель (3), алгоритм ее преобразования в статическую версию и использование автоматизированной программной системы (графоанализатора) для эффективного, многопараметрического анализа. Это, в частности, повышает практическую значимость рассмотренного в статье вопроса и стимулирует продолжение его исследования. Разработка программного модуля, автоматизированного внесения информации в пакет [4], а также представление ее в понятном для конечного пользователя (экономиста, финансового аналитика, бухгалтера и пр.) виде позволит рассматривать указанную совокупность инструментов, как удобную систему поддержки принятия инвестиционных решений при оперативном анализе инвестиционных проектов. В свою очередь, системы поддержки принятия решений являются ключевыми составляющими современных IT-проектов при разработке таких цифровых технологий, как автоматизированные рабочие места управленца (аналитика), цифровые двойники производственных процессов, предприятий, территорий.