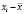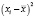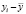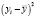Введение
В современных условиях становится необходимым построение статистически значимого уравнения линейной регрессии, объясняющей динамику валового внутреннего продукта РФ от экспорта РФ, проверка надежности модели методом тестирования случайных остатков с помощью тестов Голдфелда-Квандта, ранговой корреляции Спирмена, Глейзера, Парка, Уайта, Бройша-Пагана, разработка прогноза ВВП России и интерпретация полученных результатов.
Материал и методы исследования
При оценке параметров уравнения регрессии применяется традиционный метод наименьших квадратов. Проводится проверка гомо-, гетероскедастичности остатков в парной регрессии. Последовательно рассматриваются тесты: Голдфелда-Квандта, ранговой корреляции Спирмена, Глейзера, Парка, Уайта, критерий Бройша-Пагана.
Результаты исследования и их обсуждение
Наличие гетероскедастичности в остатках может привести к смещенности оценок коэффициентов регрессии, хотя несмещенность оценок в основном зависит от соблюдения предположения о независимости остатков и величин факторов, т.е. cov(x,u) = 0.
Гетероскедастичность будет сказываться на уменьшении эффективности оценок параметров. В частности, невозможно использовать формулу стандартной ошибки коэффициентов σai, предполагающей единую дисперсию остатков.
Рассмотрим зависимость от использованного валового внутреннего продукта (ВВП, трлн руб.) – y от экспорта России – x (трлн руб.) в таблице 1.
Таблица 1
Зависимость использованного ВВП от экспорта России
|
Год |
1997 г. |
1998 г. |
1999 г. |
2000 г. |
2001 г. |
2002 г. |
2003 г. |
2004 г. |
2005 г. |
|
y |
2,3 |
2,6 |
4,8 |
7,3 |
8,9 |
10,8 |
13,2 |
17 |
21,6 |
|
x |
0,58 |
0,82 |
2,08 |
3,22 |
3,3 |
3,81 |
4,66 |
5,86 |
7,61 |
|
Год |
2006 г. |
2007 г. |
2008 г. |
2009 г. |
2010 г. |
2011 г. |
2012 г. |
2013 г. |
2014 г. |
|
y |
26,9 |
33,2 |
41,3 |
38,8 |
46,3 |
56 |
68,1 |
73 |
79 |
|
x |
9,08 |
10,03 |
12,92 |
10,84 |
13,53 |
16,94 |
18,32 |
18,86 |
21,43 |
|
Год |
2015 г. |
2016 г. |
2017 г. |
2018 г. |
2019 г. |
2020 г. |
|||
|
y |
83,1 |
85,6 |
91,8 |
103,9 |
109,2 |
107 |
|||
|
x |
23,85 |
22,14 |
23,96 |
31,98 |
31,17 |
27,3 |
Таблица 2
Расчет параметров парной линейной регрессии
|
№ |
yi |
xi |
x∙y |
x2 |
|
|
|
|
|
|
|
ui |
ui2 |
|
1 |
2,3 |
0,6 |
1 |
0,3 |
-12,9 |
167,3 |
-44,82 |
2009,1 |
-0,8 |
-48 |
2302 |
3 |
10 |
|
2 |
2,6 |
0,8 |
2 |
0,7 |
-12,7 |
161,1 |
-44,54 |
1983,5 |
0,1 |
-47 |
2216 |
3 |
6 |
|
3 |
4,8 |
2,1 |
10 |
4,3 |
-11,4 |
130,6 |
-42,34 |
1792,9 |
4,8 |
-42 |
1797 |
0 |
0 |
|
4 |
7,3 |
3,2 |
24 |
10,4 |
-10,3 |
106,0 |
-39,86 |
1588,8 |
9,0 |
-38 |
1458 |
-2 |
3 |
|
5 |
8,9 |
3,3 |
30 |
10,9 |
-10,2 |
104,3 |
-38,22 |
1460,9 |
9,3 |
-38 |
1435 |
0 |
0 |
|
6 |
10,8 |
3,8 |
41 |
14,5 |
-9,7 |
94,1 |
-36,34 |
1320,3 |
11,2 |
-36 |
1294 |
0 |
0 |
|
7 |
13,2 |
4,7 |
61 |
21,7 |
-8,9 |
78,4 |
-33,96 |
1153,1 |
14,3 |
-33 |
1079 |
-1 |
1 |
|
8 |
17,0 |
5,9 |
100 |
34,3 |
-7,7 |
58,6 |
-30,14 |
908,3 |
18,8 |
-28 |
806 |
-2 |
3 |
|
9 |
21,6 |
7,6 |
164 |
57,9 |
-5,9 |
34,9 |
-25,56 |
653,1 |
25,3 |
-22 |
480 |
-4 |
13 |
|
10 |
26,9 |
9,1 |
244 |
82,4 |
-4,4 |
19,7 |
-20,25 |
410,0 |
30,7 |
-16 |
270 |
-4 |
14 |
|
11 |
33,2 |
10,0 |
333 |
100,6 |
-3,5 |
12,1 |
-13,92 |
193,7 |
34,2 |
-13 |
167 |
-1 |
1 |
|
12 |
41,3 |
12,9 |
533 |
167,0 |
-0,6 |
0,3 |
-5,89 |
34,7 |
45,0 |
-2 |
5 |
-4 |
14 |
|
13 |
38,8 |
10,8 |
421 |
117,5 |
-2,7 |
7,1 |
-8,36 |
69,9 |
37,3 |
-10 |
98 |
2 |
2 |
|
14 |
46,3 |
13,5 |
627 |
183,0 |
0,0 |
0,0 |
-0,86 |
0,7 |
47,2 |
0 |
0 |
-1 |
1 |
|
15 |
56,0 |
16,9 |
948 |
287,0 |
3,4 |
11,8 |
8,80 |
77,5 |
59,9 |
13 |
162 |
-4 |
15 |
|
16 |
68,1 |
18,3 |
1248 |
335,8 |
4,8 |
23,2 |
20,94 |
438,4 |
65,0 |
18 |
319 |
3 |
10 |
|
17 |
73,0 |
18,9 |
1377 |
355,8 |
5,4 |
28,6 |
25,82 |
666,7 |
67,0 |
20 |
394 |
6 |
36 |
|
18 |
79,0 |
21,4 |
1693 |
459,1 |
7,9 |
62,6 |
31,86 |
1015,3 |
76,5 |
29 |
862 |
3 |
6 |
|
19 |
83,1 |
23,8 |
1982 |
568,8 |
10,3 |
106,8 |
35,92 |
1290,4 |
85,5 |
38 |
1470 |
-2 |
6 |
|
20 |
85,6 |
22,1 |
1895 |
490,0 |
8,6 |
74,4 |
38,45 |
1478,4 |
79,2 |
32 |
1023 |
6 |
42 |
|
21 |
91,8 |
24,0 |
2201 |
574,2 |
10,5 |
109,2 |
44,68 |
1996,1 |
85,9 |
39 |
1503 |
6 |
35 |
|
22 |
103,9 |
32,0 |
3322 |
1022,9 |
18,5 |
341,1 |
56,70 |
3214,4 |
115,7 |
69 |
4694 |
-12 |
140 |
|
23 |
109,2 |
31,2 |
3405 |
971,8 |
17,7 |
311,9 |
62,08 |
3853,4 |
112,7 |
66 |
4292 |
-3 |
12 |
|
24 |
107,0 |
27,3 |
2920 |
745,4 |
13,8 |
190,1 |
59,80 |
3576,2 |
98,3 |
51 |
2616 |
9 |
75 |
|
Сред. |
47 |
14 |
983 |
276 |
Сумма |
2 234 |
31 186 |
1132 |
30741 |
445 |
Проблема гетероскедастичности характерна для перекрестных данных и редко встречается при рассмотрении временных рядов. Для проверки условия теоремы Гаусса-Маркова о гомоскедастичности случайного остатка в модели может использоваться несколько тестов: тест Голдфелда-Квандта, тест ранговой корреляции Спирмена, тест Глейзера, тест Парка, тест Уайта, критерий Бройша-Пагана.
Последовательно рассмотрим эти тесты.
.
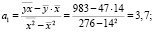
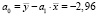Получаем уравнение регрессии:
.
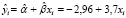1. Проведение оценки параметров парной линейной регрессии будем проводить с помощью инструмента «Регрессия» пакета «Анализа данных», а также с помощью функции «Линейн» табличного процессора Excel (табл. 2).
Проведем оценку тесноты и силы связи между переменными x и y.
Для проведения оценки тесноты связи между переменными x и y используем коэффициент корреляции и коэффициент детерминации.
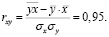
По шкале Чеддока можно сделать вывод, что связь высокая.
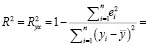
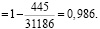
Полученное значение свидетельствует: на формирование объясняемой переменной в размере 98,6% оказывает влияние объясняющая переменная.
Оценку силы связи между объясняемой и объясняющей переменных выполним, используя значение среднего коэффициента эластичности:
Э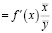 
= 
= 
.
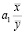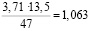Тем самым при изменении объясняющей переменной на 1% объясняемая переменная изменится в 1,063 раза.
Оценка значимости уравнения регрессии проводится с помощью F-критерия Фишера (F-теста), который состоит в проверке гипотезы о статистической незначимости уравнения регрессии. Для этого сравниваются значения фактического Fрасч полученной парной регрессии и критического (табличного) Fкрит значений F-критерия Фишера.
Fрасч=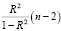
= 
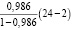= 1519,
Fрасч > Fкрит, 1519 > 4,3.
Тем самым отклоняется статистическая гипотеза Н0: a1 = 0 и делается вывод, что качество регрессии удовлетворительно.
Качество полученной регрессии определим через среднюю ошибку аппроксимации:
Асред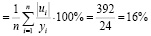 
,
т.е. в среднем оцененные значения объясняемой переменной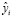 
отклоняются от фактических yi на 16%, что входит в допустимый предел значений.
2. Проверка остатков полученной парной линейной регрессии на гомоскедастичность.
2.1. Тест Голфельда-Квандта.
Таблица 3
Расчет тест Голфельда-Квандта
|
№ наблюдения |
y |
х |
|
|
1 |
2,3 |
0,58 |
|
|
2 |
2,6 |
0,82 |
|
|
3 |
4,8 |
2,08 |
|
|
4 |
7,3 |
3,22 |
|
|
5 |
8,9 |
3,30 |
|
|
6 |
10,8 |
3,81 |
|
|
7 |
13,2 |
4,66 |
|
|
8 |
17,0 |
5,86 |
|
|
9 |
21,6 |
7,61 |
|
|
10 |
26,9 |
9,08 |
|
|
11 |
33,2 |
10,03 |
|
|
12 |
41,3 |
12,92 |
|
|
13 |
38,8 |
10,84 |
|
|
14 |
46,3 |
13,53 |
|
|
15 |
56,0 |
16,94 |
|
|
16 |
68,1 |
18,32 |
|
|
17 |
73,0 |
18,86 |
|
|
18 |
79,0 |
21,43 |
|
|
19 |
83,1 |
23,85 |
|
|
20 |
85,6 |
22,14 |
|
|
21 |
91,8 |
23,96 |
|
|
22 |
103,9 |
31,98 |
|
|
23 |
109,2 |
31,17 |
|
|
24 |
107,0 |
27,30 |
Исходные данные для переменных х и у отсортируем по возрастанию значений х, а затем разобьем весь исходный массив из 24 значений на два равных подмассива по 12 значений каждый (табл. 3).
Для первого и второго подмассивов найдем значения RSS (RSS1 – для первого (верхнего) подмассива из 12 значений, RSS2 – для второго (нижнего) подмассива из 12 значений). Для этого воспользуемся инструментом Регрессия. Для первой совокупности:
RSS1 = 18,5; RSS2 = 340;
GQ = 18,46 / 340 = 0,05;
GQ–1 = 0,05–1 = 18,42.
Для сравнения полученных значений GQ и GQ–1 с Fкрит найдем его значение при степени свободы, равной 10. Fкрит = 2,98. Полученные значения GQ–1 > Fкрит, тем самым не подтверждается статистическая гипотеза о равенстве дисперсий случайных остатков в наблюдаемых уравнениях. Остатки обладают гетероскедастичностью.
2.2. Тест ранговой корреляции Спирмена (табл. 4).
Для начала необходимо определить остатки u между исходными (статистическими) значениями переменной y и полученными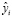 
в результате оценки парной линейной регрессии. Для этого можно воспользоваться инструментов Регрессия табличного процессора Excel. В качестве исходных данных задаем значения y и x и отмечаем пункт остатки.
Ранжируем значения x и u с использованием функции РАНГ табличного процессора Excel и находим значение D как разницу рангов, затем полученные значения возводим в квадрат.
Таблица 4
Расчет ранговой корреляции Спирмена
|
№ наблюдения |
y |
x |
|u| |
Ранг Х |
Ранг U |
D |
D2 |
|
1 |
2,3 |
0,58 |
3,2 |
1 |
14 |
-13 |
169 |
|
2 |
2,6 |
0,82 |
2,5 |
2 |
12 |
-10 |
100 |
|
3 |
4,8 |
2,08 |
0,0 |
3 |
1 |
2 |
4 |
|
4 |
7,3 |
3,22 |
1,7 |
4 |
8 |
-4 |
16 |
|
5 |
8,9 |
3,30 |
0,3 |
5 |
2 |
3 |
9 |
|
6 |
10,8 |
3,81 |
0,4 |
6 |
3 |
3 |
9 |
|
7 |
13,2 |
4,66 |
1,1 |
7 |
6 |
1 |
1 |
|
8 |
17,0 |
5,86 |
1,8 |
8 |
9 |
-1 |
1 |
|
9 |
21,6 |
7,61 |
3,7 |
9 |
16 |
-7 |
49 |
|
10 |
26,9 |
9,08 |
3,8 |
10 |
18 |
-8 |
64 |
|
11 |
33,2 |
10,03 |
1,0 |
11 |
5 |
6 |
36 |
|
12 |
41,3 |
12,92 |
3,7 |
13 |
17 |
-4 |
16 |
|
13 |
38,8 |
10,84 |
1,5 |
12 |
7 |
5 |
25 |
|
14 |
46,3 |
13,53 |
0,9 |
14 |
4 |
10 |
100 |
|
15 |
56,0 |
16,94 |
3,9 |
15 |
19 |
-4 |
16 |
|
16 |
68,1 |
18,32 |
3,1 |
16 |
13 |
3 |
9 |
|
17 |
73,0 |
18,86 |
6,0 |
17 |
21 |
-4 |
16 |
|
18 |
79,0 |
21,43 |
2,5 |
18 |
11 |
7 |
49 |
|
19 |
83,1 |
23,85 |
2,4 |
20 |
10 |
10 |
100 |
|
20 |
85,6 |
22,14 |
6,5 |
19 |
22 |
-3 |
9 |
|
21 |
91,8 |
23,96 |
5,9 |
21 |
20 |
1 |
1 |
|
22 |
103,9 |
31,98 |
11,8 |
24 |
24 |
0 |
0 |
|
23 |
109,2 |
31,17 |
3,4 |
23 |
15 |
8 |
64 |
|
24 |
107,0 |
27,30 |
8,7 |
22 |
23 |
-1 |
1 |
|
Сумма |
864 |
Определяем коэффициент Спирмена по формуле:
.
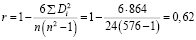На основании шкалы Чеддока определяем, что связь между фактором x и случайными остатками u прямая умеренная.
Определяем величину статистического критерия Стьюдента:
.
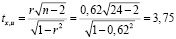tкрит = 2,07. tx,u > tкрит; 3,75 > 2,07,
то принимается, что коэффициент ранговой корреляции статистически значим и присутствует гетероскедастичность остатков.
2.3. Тест Глейзера (табл. 5).
1. Оценим регрессию y по x, чтобы найти абсолютные значения остатков.
2. Рассчитаем уравнения регрессии ui от x–γ при значениях γ:= –1; –0,5; 0,5; 1; 1,5 по формуле:
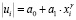
Варьирование значение γ от – 1 до + 1 позволяет подобрать наиболее адекватную модель. Для каждого значения γ проверяется статистическая значимость параметра a1 c помощью критерия Стьюдента.
Если для некоторых γ параметр a1 признается значимым (тестовая статистика больше критического значения), то и гетероскедастичность данного вида признается значимой. При этом среди анализируемых моделей выбирается модель с тем значением γ, для которого параметр a1 наиболее значим (с наибольшим значением тестовой статистики).
Таблица 5
Расчет теста Глейзера
|
№ наблюдения |
y |
x |
Остатки|u| |
x–1 |
x–0,5 |
x0,5 |
x1,5 |
|
1 |
2,3 |
0,6 |
3,151 |
1,726 |
1,314 |
0,8 |
0,4 |
|
2 |
350 |
385 |
2,542 |
0,003 |
0,051 |
19,6 |
7 554 |
|
3 |
330 |
545 |
0,048 |
0,002 |
0,043 |
23,3 |
12 723 |
|
4 |
425 |
680 |
1,677 |
0,001 |
0,038 |
26,1 |
17 732 |
|
5 |
502 |
810 |
0,338 |
0,001 |
0,035 |
28,5 |
23 053 |
|
6 |
360 |
780 |
0,359 |
0,001 |
0,036 |
27,9 |
21 784 |
|
7 |
420 |
790 |
1,105 |
0,001 |
0,036 |
28,1 |
22 204 |
|
8 |
505 |
785 |
1,754 |
0,001 |
0,036 |
28,0 |
21 994 |
|
9 |
280 |
400 |
3,651 |
0,003 |
0,050 |
20,0 |
8 000 |
|
10 |
305 |
530 |
3,804 |
0,002 |
0,043 |
23,0 |
12 201 |
|
11 |
340 |
580 |
0,996 |
0,002 |
0,042 |
24,1 |
13 968 |
|
12 |
460 |
720 |
3,704 |
0,001 |
0,037 |
26,8 |
19 319 |
|
13 |
440 |
700 |
1,548 |
0,001 |
0,038 |
26,5 |
18 520 |
|
14 |
415 |
690 |
0,919 |
0,001 |
0,038 |
26,3 |
18 124 |
|
15 |
345 |
650 |
3,915 |
0,002 |
0,039 |
25,5 |
16 571 |
|
16 |
405 |
760 |
3,087 |
0,001 |
0,036 |
27,6 |
20 951 |
|
17 |
450 |
780 |
5,972 |
0,001 |
0,036 |
27,9 |
21 784 |
|
18 |
515 |
840 |
2,511 |
0,001 |
0,035 |
29,0 |
24 345 |
|
19 |
390 |
590 |
2,419 |
0,002 |
0,041 |
24,3 |
14 331 |
|
20 |
370 |
540 |
6,465 |
0,002 |
0,043 |
23,2 |
12 548 |
|
21 |
435 |
660 |
5,914 |
0,002 |
0,039 |
25,7 |
16 955 |
|
22 |
458 |
685 |
11,815 |
0,001 |
0,038 |
26,2 |
17 928 |
|
23 |
490 |
750 |
3,435 |
0,001 |
0,037 |
27,4 |
20 539 |
|
24 |
485 |
760 |
8,654 |
0,001 |
0,036 |
27,6 |
20 951 |
tкрит = 2,06 > tрасчет1 (0,06), tрасчет2 (0,06), tрасчет3 (0,01), tрасчет4 (0,1).
Параметр a1 статистически незначим во всех уравнениях регрессии, доказана гомоскедастичность остатков.
2.4. Тест Парка (табл. 6).
Тест используется для проверки гетероскедастичности случайных ошибок регрессионной модели. Предполагается, что дисперсия σ2 является функцией -го значения объясняющей переменной х. Р. Парк предложил для проведения исследования на гетероскедастичность использовать дополнительно функциональную зависимость вида (прологарифмировано):
ln(u2) = a0 + a1 · ln(x) + w.
Так как дисперсии σi2 обычно неизвестны, их заменяют оценками квадратов отклонений ошибок u2. Критерий Парка, как правило, один не применяется, а дополняется другими тестами.
Для этого построим ряды ln(u2) и ln(x), а затем проведем оценку ее параметров с использованием инструмента Регрессия.
tкрит = 2,06; tрасчет = 2,82; tкрит < tрасчет.
Таким образом, коэффициент a1 является значимым. Следовательно, гетероскедастичность остатков доказана.
2.5. Тест Уайта (табл. 7).
Тест предложен Уайтом в 1980 г. Это универсальная процедура тестирования гетероскедастичности случайных ошибок линейной регрессионной модели, не налагающая особых ограничений на структуру гетероскедастичности.
Применяем инструмент Регрессия.
Fрасч > Fкрит, 12,2 > 3,5.
Принимается гипотеза о гетероскедастичности остатков уравнения.
Таблица 6
Расчет теста Парка
|
y |
x |
Остатки|u| |
ln(u2) |
ln(x) |
|
2,3 |
0,6 |
3,2 |
2,30 |
-0,55 |
|
2,6 |
0,8 |
2,5 |
1,87 |
-0,20 |
|
4,8 |
2,1 |
0,0 |
-6,07 |
0,73 |
|
7,3 |
3,2 |
-1,7 |
1,03 |
1,17 |
|
8,9 |
3,3 |
-0,3 |
-2,17 |
1,19 |
|
10,8 |
3,8 |
-0,4 |
-2,05 |
1,34 |
|
13,2 |
4,7 |
-1,1 |
0,20 |
1,54 |
|
17,0 |
5,9 |
-1,8 |
1,12 |
1,77 |
|
21,6 |
7,6 |
-3,7 |
2,59 |
2,03 |
|
26,9 |
9,1 |
-3,8 |
2,67 |
2,21 |
|
33,2 |
10,0 |
-1,0 |
-0,01 |
2,31 |
|
41,3 |
12,9 |
-3,7 |
2,62 |
2,56 |
|
38,8 |
10,8 |
1,5 |
0,87 |
2,38 |
|
46,3 |
13,5 |
-0,9 |
-0,17 |
2,60 |
|
56,0 |
16,9 |
-3,9 |
2,73 |
2,83 |
|
68,1 |
18,3 |
3,1 |
2,25 |
2,91 |
|
73,0 |
18,9 |
6,0 |
3,57 |
2,94 |
|
79,0 |
21,4 |
2,5 |
1,84 |
3,06 |
|
83,1 |
23,8 |
-2,4 |
1,77 |
3,17 |
|
85,6 |
22,1 |
6,5 |
3,73 |
3,10 |
|
91,8 |
24,0 |
5,9 |
3,55 |
3,18 |
|
103,9 |
32,0 |
-11,8 |
4,94 |
3,47 |
|
109,2 |
31,2 |
-3,4 |
2,47 |
3,44 |
|
107,0 |
27,3 |
8,7 |
4,32 |
3,31 |
Таблица 7
Расчет теста Уайта
|
x |
x2 |
Остатки|u| |
|u|2 |
|
0,58 |
0,34 |
3,2 |
9,9 |
|
0,82 |
0,67 |
2,5 |
6,5 |
|
2,08 |
4,35 |
0,0 |
0,0 |
|
3,22 |
10,36 |
1,7 |
2,8 |
|
3,30 |
10,89 |
0,3 |
0,1 |
|
3,81 |
14,54 |
0,4 |
0,1 |
|
4,66 |
21,68 |
1,1 |
1,2 |
|
5,86 |
34,34 |
1,8 |
3,1 |
|
7,61 |
57,87 |
3,7 |
13,3 |
|
9,08 |
82,43 |
3,8 |
14,5 |
|
10,03 |
100,58 |
1,0 |
1,0 |
|
12,92 |
167,02 |
3,7 |
13,7 |
|
10,84 |
117,55 |
1,5 |
2,4 |
|
13,53 |
183,04 |
0,9 |
0,8 |
|
16,94 |
286,99 |
3,9 |
15,3 |
|
18,32 |
335,80 |
3,1 |
9,5 |
|
18,86 |
355,83 |
6,0 |
35,7 |
|
21,43 |
459,07 |
2,5 |
6,3 |
|
23,85 |
568,77 |
2,4 |
5,9 |
|
22,14 |
489,98 |
6,5 |
41,8 |
|
23,96 |
574,21 |
5,9 |
35,0 |
|
31,98 |
1 022,87 |
11,8 |
139,6 |
|
31,17 |
971,79 |
3,4 |
11,8 |
|
27,30 |
745,37 |
8,7 |
74,9 |
2.6. Тест Бройша-Пагана (табл. 8).
Тест применяется, если имеются основания полагать, что дисперсия ошибок может зависеть от некоторой совокупности наблюдаемых переменных. Воспользуемся данными предыдущего теста и найдем оценку дисперсии случайного члена по формуле:
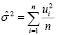
Расчет значений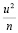 
приведен в табл. 8.
.
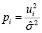Применяем инструмент Регрессия. Оценим параметры модели и найдем статистику χ2m–1 = ESS / 2. χ2m–1 = 19. Определим χ2крит при а = 0,05, v2 = 22, χ2m–1 < χ2крит, так как 19 < 33. Принимается гипотеза о гомоскедастичности остатков.
Сведем результаты проведенных тестов на проверку остатков полученной парной регрессии на гомоскедастичность в табл. 9.
Таблица 8
Расчет теста Бройша-Пагана
|
y |
x |
Остатки|u| |
pi |
|
2,3 |
0,6 |
3,15 |
0,54 |
|
2,6 |
0,8 |
2,54 |
0,35 |
|
4,8 |
2,1 |
0,05 |
0,00 |
|
7,3 |
3,2 |
-1,68 |
0,15 |
|
8,9 |
3,3 |
-0,34 |
0,01 |
|
10,8 |
3,8 |
-0,36 |
0,01 |
|
13,2 |
4,7 |
-1,10 |
0,07 |
|
17,0 |
5,9 |
-1,75 |
0,17 |
|
21,6 |
7,6 |
-3,65 |
0,72 |
|
26,9 |
9,1 |
-3,80 |
0,78 |
|
33,2 |
10,0 |
-1,00 |
0,05 |
|
41,3 |
12,9 |
-3,70 |
0,74 |
|
38,8 |
10,8 |
1,55 |
0,13 |
|
46,3 |
13,5 |
-0,92 |
0,05 |
|
56,0 |
16,9 |
-3,92 |
0,83 |
|
68,1 |
18,3 |
3,09 |
0,51 |
|
73,0 |
18,9 |
5,97 |
1,92 |
|
79,0 |
21,4 |
2,51 |
0,34 |
|
83,1 |
23,8 |
-2,42 |
0,32 |
|
85,6 |
22,1 |
6,46 |
2,25 |
|
91,8 |
24,0 |
5,91 |
1,89 |
|
103,9 |
32,0 |
-11,82 |
7,52 |
|
109,2 |
31,2 |
-3,44 |
0,64 |
|
107,0 |
27,3 |
8,65 |
4,04 |
Таблица 9
Итоговая таблица
|
№ п/п |
Название теста |
Результат тестирования остатков |
|
1 |
Голдфелда-Квандта (тест GQ) |
Гетероскедастичные |
|
2 |
Ранговой корреляции Спирмена |
Гетероскедастичные |
|
3 |
Глейзера |
Гомоскедастичные |
|
4 |
Парка |
Гетероскедастичные |
|
5 |
Уайта |
Гетероскедастичные |
|
6 |
Бройша-Пагана |
Гомоскедастичные |
Заключение
Полученные результаты в целом позволяют оценить регрессионное уравнение как надежное, и его можно использовать в практической деятельности анализа макроэкономических показателей России. Для соблюдения экономической безопасности страны ежегодный рост ВВП должен составлять 5% (с учетом роста цен). Спрогнозируем уровень экспорта, который необходим для выполнения этого требования, согласно полученному уравнению:
.
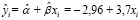К 2022 году ВВП должен составить 115 трлн руб., следовательно, России необходимо достичь уровня экспорта в размере 31,9 трлн руб.