Введение
Напомним, что в этой работе, как и в более ранней работе научного руководителя автора – профессора Халикова М.А. [1], под рабочим капиталом предприятия (в данном случае, производственного) понимаются постоянные и переменные активы, покрывающие соответствующие затраты его операционного сегмента и финансируемые из собственных и заемных источников, включающих собственный капитал и краткосрочные кредиты. Эффективность рыночной деятельности предприятия существенно зависит от величины постоянных и переменных активов, позволяющей обеспечить выпуск продукции ассортиментного ряда предприятия в условиях изменчивого спроса на его продукцию, а также от соотношения долей собственного и заемного финансирования (структуры капитала) операционного сегмента, влияющих как на уровень риска банкротства (с одной стороны), так и на показатели рентабельности собственного капитала в условиях свободного доступа к денежным ресурсам кредитного рынка (с другой).
Моделирование оптимального по экономическому критерию размера операционного сегмента производственной корпорации с учетом непостоянного характера рыночных цен и спроса на продукцию предприятия и используемые в производстве активы рабочего капитала – актуальная и малоизученная область инструментального сопровождения рыночной деятельности хозяйствующего в условиях высокой неопределенности и риска его внешней и внутренней среды субъекта.
Цель статьи – разработать теоретическую концепцию и построить математическую модель выбора оптимального по экономическому критерию объема и состава постоянных и переменных активов рабочего капитала производственной корпорации и структуры капитала, покрывающего затраты ее производственной деятельности, с учетом факторов сопутствующих рисков и неопределенности параметров товарных и финансовых рынков.
Материалы и методы исследования
Основной работой по рассматриваемой тематике является статья М.А. Горского и М.А. Халикова [1], в которой заявлена постановка задачи моделирования оптимального размера производственного сегмента предприятия в условиях детерминированных параметров макроэкономической среды. Также похожие постановки задач исследования оптимальных вариантов производственной деятельности предприятия и, в том числе, с использованием аппарата производственных функций, без и с учетом риска представлены в работах: А.М. Антиколь, М.А. Халикова [2], М.А. Бендикова и И.Э. Фролова [3], М.А. Горского [4,5,6], В.А. Колемаева [7], Б. Коласса [8], М. Круи [9], М.А. Халикова, А.И. Дерябиной, Д.А. Лях [10], О.Е. Хрусталева [11], М.А. Горского и Е.М. Решульской [12], Ф. Турино [13] и П. Самуэльсона [14].
Проблематика выбора критериев оптимальности производственной деятельности предприятия в условиях растущих или, наоборот, падающих рынков, которая также поднимается в статье, отражена в работах Д.А. Безухова [15], М.А. Никифоровой и М.А. Халикова [16, 17], М.А. Халикова, Е.С. Кулинченко, А.А. Струковой [18]. Математический инструментарий и численные алгоритмы решения задач линейной и нелинейной, непрерывной и дискретной оптимизации заимствованы из работ М.А. Горского [19], М.А. Горского, М.А. Халикова, Д.А. Максимова [20].
Результаты исследования и их обсуждения
Рассмотрим компоненту модели, связанную со структурой пассива рабочего капитала PK(t) предприятия на плановом интервале t (t = 1,T) и особенностями финансирования затрат предприятия из собственных и заемных источников. Если CK(t) и ЗK(t) – соответственно собственный и заемный капитал, покрывающие затраты операционного сегмента предприятия на интервале t, то коэффициент β(t) автономии пассива рабочего капитала (коэффициент риска его структуры) определяется по формуле:
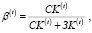 (1)
(1)
откуда объем заемного финансирования и величина пассива рабочего капитала (объем возможного покрытия затрат производственной деятельности предприятия из собственных и заемных источников) могут быть определены по формулам:
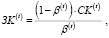 (2)
(2)
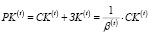 (3)
(3)
С другой стороны, объем заемного финансирования не может превысить определенную кредитной организацией для периода t величину ЗKO(t), что, в свою очередь, ограничивает выбор варианта структуры рабочего капитала для периода t, задаваемой коэффициентом β(t):
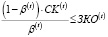 (4)
(4)
или
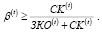 (4’)
(4’)
Если β(t) – предельное значение коэффициента автономии структуры рабочего капитала, установленное ЛПР (лицом принимающим решение) для периода t, то при выборе структуры рабочего капитала для этого периода следует принимать в расчет следующий диапазон возможных значений коэффициента автономии:
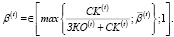 (5)
(5)
Ясно, что ставка ρ(t) заемного финансирования для случая рискового кредитования выражается нелинейной зависимостью:
ρ(t) = ρ(β(t)), (6)
форма которой должна уточняться для конкретной пары «кредитор-заемщик» с учетом как кредитной истории заемщика, так и отношения кредитора к риску (проблематика моделирования нелинейной зависимости в паре: «коэффициент автономии рабочего капитала – ставка по внешнему кредиту» изучена недостаточно. Некоторые ее аспекты предполагается осветить в следующих работах автора. Здесь же сошлемся на результаты исследования М.А. Халикова и А.М. Антиколь, представленные в работе [2]).
Если дополнительно предположить, что финансирование инвестиций в постоянные и переменные активы рабочего капитала предприятия с целью роста его производственно-технологического потенциала на шаге t осуществляется из дополнительных источников финансирования, то общий объем ΔPK(t) инвестиционных затрат не превышает величины 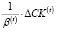 (где β(t) и ΔСK(t) – регулируемые (управляемые) параметры операционного сегмента предприятия), а взвешенные по составляющим рабочего капитала затраты на его обслуживание составят величину:
(где β(t) и ΔСK(t) – регулируемые (управляемые) параметры операционного сегмента предприятия), а взвешенные по составляющим рабочего капитала затраты на его обслуживание составят величину:
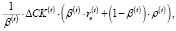 (7)
(7)
где re(t) – цена собственного капитала предприятия, рассчитанная для временного интервала t по модифицированной модели CAPM, предложенной Р. Хамадой [8, 13], ρ(t) – ставка по внешнему кредиту, рассчитанная по формуле (6).
В формулах (1) – (5) следует дополнительно учесть условие достаточности финансирования операционного сегмента предприятия на очередном временном интервале t из собственных источников:
ΔСK(t) ≤ СKO(t–1), t = 2,T , (8)
где СKO(t–1) – объем собственных средств предприятия на конец временного интервала t–1, выделенных на производственные инвестиции.
Следующая компонента модели включает оценки структуры и затрат на обслуживание активов рабочего капитала операционного сегмента предприятия. Введем следующие обозначения: J – число учитываемых в модели постоянных и переменных активов (j – индекс актива); 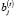 – оценка производственного потенциала операционной сферы предприятия по j-му активу на начало временного интервала t (в натуральном или стоимостном выражениях);
– оценка производственного потенциала операционной сферы предприятия по j-му активу на начало временного интервала t (в натуральном или стоимостном выражениях); 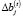 – изменение (рост) величины j-го актива в временном интервале t (t = 1,T–1); αj – коэффициент амортизации, а
– изменение (рост) величины j-го актива в временном интервале t (t = 1,T–1); αj – коэффициент амортизации, а 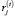 – затраты на приобретение, освоение и обслуживание единицы j-го актива на временном интервале t.
– затраты на приобретение, освоение и обслуживание единицы j-го актива на временном интервале t.
С учетом введенных обозначений запишем соотношения для оценки составляющих рабочего капитала и ограничение по объему затрат на их обслуживание:
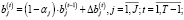 (9)
(9)
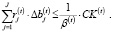 (10)
(10)
Основным компонентом модели является «стандартная» планово-производственная задача Канторовича в статичной постановке с критерием на максимум валового маржинального дохода операционного сегмента от производства и реализации изделий производственной программы и сдачи в аренду неиспользуемых производственных активов предприятия и ограничением на рыночный риск на временном интервале t:
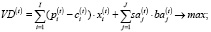 (11)
(11)
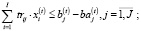 (12)
(12)
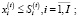 (13)
(13)
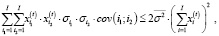 (14)
(14)
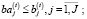 (15)
(15)
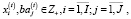 (16)
(16)
где VD(t) – валовый маржинальный доход, получаемый в операционном сегменте предприятия в периоде t; i, i1, i2 – индексы изделий производственной программы предприятия (i, i1, i2 = 1,I); 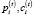 – соответственно цена реализации и удельные затраты на производство i-го изделия в интервале планирования t; trij – технологическая фондоёмкость i-го изделия по j-му активу;
– соответственно цена реализации и удельные затраты на производство i-го изделия в интервале планирования t; trij – технологическая фондоёмкость i-го изделия по j-му активу; 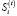 – рыночный спрос на i-е изделие производственной программы предприятия на временном интервале t;
– рыночный спрос на i-е изделие производственной программы предприятия на временном интервале t; 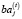 – неиспользуемый остаток j-го актива, сдаваемый в интервале t в аренду по ставке
– неиспользуемый остаток j-го актива, сдаваемый в интервале t в аренду по ставке 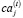 ; σi – дисперсия доходности продукции i-го вида за период наблюдения; cov(i1;i2) – ковариация доходностей изделий с индексами i1 и i2 (за период наблюдения); σ – принимаемое ЛПР пороговое значение риска производственной программы.
; σi – дисперсия доходности продукции i-го вида за период наблюдения; cov(i1;i2) – ковариация доходностей изделий с индексами i1 и i2 (за период наблюдения); σ – принимаемое ЛПР пороговое значение риска производственной программы.
В дискретной задаче (11) – (16) экзогенными параметрами являются рыночные цены, спрос и удельные затраты, формирующиеся под влиянием рыночных факторов спроса и предложения. Эндогенными (управляемыми) параметрами являются объемы 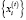 планируемой к выпуску продукции и остатки
планируемой к выпуску продукции и остатки 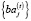 активов производственного назначения, планируемые для передачи в аренду на платной основе.
активов производственного назначения, планируемые для передачи в аренду на платной основе.
Опираясь на формальную постановку задачи (11) – (16) и учитывая соотношения (1) – (10), задающие оценки и ограничения отдельных элементов и в целом структуры рабочего капитала операционного сегмента предприятия, уточним целевой критерий и систему ограничений статичного варианта модели выбора оптимального варианта деятельности операционного сегмента предприятия на временном интервале t.
Критерием, учитывая возможность альтернативного использования капитала, привлекаемого в операционный сегмент предприятия, обоснованно принять следующую модификацию показателя EVA экономической добавленной стоимости, формируемой в этом сегменте:
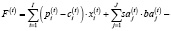
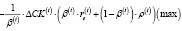 (17)
(17)
Управляемыми параметрами модели для временного интервала t являются: коэффициент β(t) автономии структуры рабочего капитала; объем CK(t) собственного капитала, направляемого в операционный сегмент для финансирования затрат производственной деятельности; 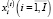 – объемы выпускаемой продукции номенклатурного перечня предприятия;
– объемы выпускаемой продукции номенклатурного перечня предприятия; 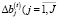 ) – составляющие постоянных и переменных активов, приобретаемые в целях увеличения производственной мощности операционного сегмента;
) – составляющие постоянных и переменных активов, приобретаемые в целях увеличения производственной мощности операционного сегмента; 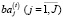 – составляющие постоянных и переменных активов, не задействованные в технологическом процессе и передаваемые в краткосрочную аренду, а также предельные уровни β(t) и σ соответственно рисков структуры рабочего капитала и рыночного.
– составляющие постоянных и переменных активов, не задействованные в технологическом процессе и передаваемые в краткосрочную аренду, а также предельные уровни β(t) и σ соответственно рисков структуры рабочего капитала и рыночного.
Управляемые параметры удовлетворяют внутри периодным ограничениям: (5), (8), (10), (12), (13), (14), (15), (16) и межпериодному ограничению (9), связывающему объемы активов рабочего капитала на последовательных временных интервалах.
Экзогенными для рассматриваемой модели являются параметры товарного и финансового рынков:
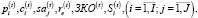
В модели присутствуют технологические:
trij (i = 1,I; j = 1,J)
и внутрифирменные:
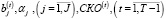
константы, которые могут считаться стартовыми параметрами модели, а также модуль формирования аналитической зависимости (6) ставки заемного финансирования от уровня риска структуры рабочего капитала.
Представленные выше компоненты позволяют представить формализованную математическую модель определения оптимального по критерию экономической добавленной стоимости размера операционного сегмента предприятия, понимаемого как структура и состав его постоянных, переменных активов и учитываемых в пассивах собственных и заемных средств.
Модель включает: критерий в форме (17) и ограничения (5), (8) – (10), (12) – (16).
Основная идея выбора оптимальной структуры рабочего капитала предприятия заключается в «параметрической» настройке управляемых параметров величин собственного и заемного финансирования операционного сегмента предприятия под текущие изменения перечисленных выше неуправляемых параметров товарного и финансового рынков.
В алгоритмическом плане задача (17), (5), (8) – (10), (12) – (16) относится к нелинейным целочисленным задачам большой размерности, для которых в силу их NP-полноты отсутствуют конструктивные численные методы поиска оптимального решения, но существуют методы локальной оптимизации, ориентированные на поиск квазиоптимального решения с заранее известной точностью, например, представленные в работе М.А. Горского [4].
Заключение
В статье рассмотрены постановка задачи и формальная модель определения оптимального размера операционного (производственного) сегмента предприятия с учетом изменчивых параметров товарных и финансовых рынков и сопутствующих производственной деятельности предприятия корпоративного сектора экономики рисков. Основное внимание уделено статичному варианту модели, описывающему «настройку» операционного сегмента предприятия на очередном плановом периоде под изменившиеся параметры спроса и цен на выпускаемую продукцию, ставок и условий кредитования его производственной деятельности банковскими организациями, приоритетов его рыночной стратегии и отношения к риску.
Вне рамок статьи остался численный алгоритм решения соответствующей рассмотренной модели иерархической (двухуровневой) нелинейной дискретной задачи большой размерности. Разработка и адаптация этого алгоритма – важная научно-практическая задача, решение которой предполагается изложить в одной из последующих публикаций автора.

