Введение
Актуальным на сегодняшний день является исследование проблемы оценки влияния транспортно-логистической инфраструктуры на региональное развитие [1-3, 7-9]. Положительное влияние развития транспортно-логистической инфраструктуры на социально-экономические показатели и эффективность пространственного социально-экономического развития региона отмечен в ряде исследований [1,3,5]. Методы оценки влияния эффективности взаимодействия участников транспортно-логистической инфраструктуры региона [7], а также оценка влияния морского порта на экономический рост региона [5] представляются важными для методологии исследования. Также есть круг работ, посвященных зависимости между развитием портовой инфраструктуры и прилегающей территории [2,3,6,9].
Исследование внеотраслевого эффекта морского порта на основе анализа таких показателей как: объем дохода порта от перевалки грузов, оценка вклада портов в ВРП, доля краевых грузов в общем грузообороте порта, доля затрат на ПРР в порту от общей товарной стоимости груза, уровень использования портовых мощностей, занятость населения и налоги, предлагается использовать в [5].
В работе [12] для оценки существенности влияния инвестиций на социально-экономические показатели регионов ранее были использованы методы корреляционно-регрессионного анализа и панельных данных.
При моделировании эконометрических зависимостей для нелинейных работ существуют особенности в экономической интерпретации оценок коэффициентов регрессии. Данная работа проливает свет на обозначенную проблему на примере задачи о влиянии инвестиций на социально-экономическое развитие портовых регионов РФ.
Материалы и методы исследования
Для анализа собраны данные Федеральной службы государственной статистики [10] по 11 портовым регионам:
- данные об инвестициях пяти морских портов России (Большой порт Санкт-Петербург, Мурманск, Оля, Новороссийск, Восточный);
- статистические данные Росстата об объеме экспорта и импорта, доле занятого трудоспособного населения и уровне прожиточного минимума в портовых и близлежащих к портам регионах за период 2010-2019 гг.
Регионы, по которым проведен анализ:
- территория Большого порта Санкт-Петербург охватывает г.Санкт-Петербург, Ленинградскую и Вологодскую области;
- территория порта Мурманск охватывает Мурманскую область и Республику Карелию;
- территория порта Оля охватывает Астраханскую и Волгоградскую области;
- территория порта Новороссийск охватывает Краснодарский и Ставропольский край;
- территория порта Восточный охватывает Приморский и Хабаровский край.
В качестве целевых показателей были взяты: экспорт (млн руб.), импорт (млн руб.), численность занятых (тыс. чел.), уровень занятости (%), величина прожиточного минимума на душу трудоспособного населения (руб./мес.) и численность рабочей силы (тыс. чел.) за 2010–2019 годы (величина прожиточного минимума с 2014 года). В качестве факторного признака, характеризующего изменение портовой инфраструктуры и социально-экономических показателей припортовых регионов, в работе рассмотрена переменная, характеризующая объем инвестиций в портовый регион РФ в млн руб. [4].
В работе были использованы методы математической статистики и эконометрики. Модели оценивались методом наименьших квадратов. Анализ и обработка статистической информации проводились с использованием пакета прикладных программ Gretl и Microsoft Excel.
Целью исследования является изучение влияния транспортно-логистической инфраструктуры на региональное развитие. Задачами исследования являются выявление и оценка зависимости между развитием портовой инфраструктуры и прилегающей территории; построение моделей зависимости влияния инвестиций на социально-экономические показатели портового региона Российской Федерации на основе собранных статистических данных; описание экономического смысла оценок коэффициентов регрессии для построенных моделей.
Результаты исследования и их обсуждение
Основной части исследования предшествует работа с данными, анализ на нетипичные наблюдения, работа с пропусками данных в исследуемом массиве.
Вследствие значительных особенностей развития экономики регионов и различий в характере поступления инвестиций в припортовые регионы, их структуры, выявлено, что часть данных по отдельным регионам лучше всего описывают нелинейные модели.
Статистически значимые результаты с выполнением условий теоремы Гаусса-Маркова получены при построении различных, линейных и нелинейных моделей зависимости от инвестиций отдельно по каждому региону методом наименьших квадратов. Для оценки качества построенных моделей использованы устойчивые к гетероскедастичности робастные стандартные ошибки.
Проведено сравнение оцененных с помощью МНК моделей и отбор лучших в смысле статистического качества. Наличие взаимосвязи (на основе построенных регрессионных моделей) между объемом инвестиций в припортовые регионы и их целевыми показателями отражено в таблице 1.
Таким образом, выявлено, что примерно в 36% регионов инвестиции в портовую инфраструктуру оказывают статистически значимое влияние на импорт, в 45% – на экспорт, в 55% – на численность рабочей силы.
Приведем пример нелинейных моделей зависимости импорта региона от инвестиций в инфраструктуру морских портов в таблице 2.
Таблица 1
Чувствительность к изменению инвестиций различных целевых показателей по припортовым регионам РФ
|
п/п |
Регион РФ |
Зависимость импорта от инвестиций* |
Зависимость экспорта от инвестиций** |
Зависимость численности рабочей силы от инвестиций* |
|
1 |
г. Санкт-Петербург |
- |
- |
- |
|
2 |
Ленинградская область |
- |
+ |
+ |
|
3 |
Вологодская область |
- |
- |
- |
|
4 |
Мурманская область |
+ |
- |
+ |
|
5 |
Республика Карелия |
+ |
+ |
+ |
|
6 |
Астраханская область |
- |
- |
- |
|
7 |
Волгоградская область |
+ |
+ |
+ |
|
8 |
Краснодарский край |
- |
- |
- |
|
9 |
Ставропольский край |
- |
+ |
- |
|
10 |
Приморский край |
- |
+ |
+ |
|
11 |
Хабаровский край |
+ |
- |
+ |
Источник: аналитика автора.
Примечание:
* при уровне значимости оценок коэффициентов регрессии, стоящих при переменных регрессии, не выше 10%;
** при уровне значимости оценок коэффициентов регрессии, стоящих при переменных регрессии, не выше 5%
Таблица 2
Нелинейные модели зависимости импорта от инвестиций в инфраструктуру морских портов
|
Хабаровский край (1) |
Мурманская область |
Волгоградская область |
|
|
Вид модели |
Y=AX^2+BX+C |
Y=AX^2+BX+C |
Y= Aexp(BX) |
|
Переменные |
Coefficient (Std. Error) |
Coefficient (Std. Error) |
Coefficient (Std. Error) |
|
Investment |
−0,247146*** (0,0276871) |
−0,318777** (0,126487) |
0,00104002*** (0,000240298) |
|
Investment^2 |
1,97768e-05*** (2,71342e-06) |
5,33097e-05* (2,35526e-05) |
- |
|
Ln(Investment) |
- |
- |
- |
|
Constant |
1245,88*** (55,1957) |
787,796*** (137,610) |
104,9317*** (0,516280) |
|
R^2 |
0,842967 |
0,694078 |
0,622127 |
|
F-statistic |
58,74859 (0,000115) |
4,756261 (0,057864) |
18,73194 (0,002519) |
Источник: аналитика автора
Примечание:
* соответствует значимости оценки коэффициента при уровне значимости 10%;
** соответствует значимости оценки коэффициента при уровне значимости 5%;
*** соответствует значимости оценки коэффициента при уровне значимости 1%.
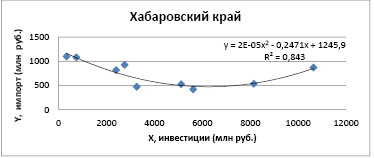
Рис. 1. Поле корреляции и линия квадратичного тренда зависимости импорта Хабаровского края от инвестиций по данным за 2010-2019 гг.
Источник: аналитика автора
Рассмотрим в качестве примера экономическую интерпретацию оценок коэффициентов регрессии в модели зависимости импорта Хабаровского края от инвестиций в припортовые регионы (табл. 2, рис. 1).
Оценка коэффициента регрессии b0 в модели (1) показывает, что при отсутствии инвестиций в порт значение импорта в среднем составит примерно 1245,88 млн руб.
Перейдем к экономическому смыслу оценок коэффициентов регрессии, стоящих при переменных. При увеличении инвестиций в инфраструктуру портового региона на 1 млн руб. объем его импорта изменится на b1 + 2b2x0 + b2 = b1 + b2(2x0 + 1) = = (−0,247+1,978e-05(2х+1)) млн руб. Соответственно, если x0 составляет 3 млрд руб., то при увеличении инвестиций на 1 млн руб. значение регионального импорта в среднем уменьшится примерно на 128,3 тыс. руб.; если x0 составляет 15 млрд руб., то при увеличении инвестиций на 1 млн руб. увеличение регионального импорта в среднем составит примерно 346,42 тыс. руб.; если x0 = 20 млрд руб., то при увеличении инвестиций на 1 млн руб. увеличение регионального импорта в среднем составит примерно 544 тыс. руб.
Для модели (1) координаты точки поворота определяем по формуле нахождения вершины параболы: xверш=6243,68 млн руб., yверш= 494,79 млн руб.; что соответствует рис. 1. При прохождении данной точки направление связи между факторным и результативным признаком меняется со снижения на рост. Следовательно, по оцененной модели для увеличения регионального импорта инвестиции в региональную инфраструктуру должны составлять более 6243,68 млн руб.
Показанный характер зависимости и наличие точки поворота может свидетельствовать о сокращении импорта вследствие недостаточности инвестиций и уровня развития портовой инфраструктуры (например, скопление грузов в портовых терминалах приводит к снижению уровня поставок), что устраняется при более высоких инвестиционных вливаниях в портовые регионы и функционирование системы на новом логистическом уровне.
Примеры построенных моделей зависимости экспорта региона от инвестиций в инфраструктуру морских портов в таблице 3.
Рассмотрим смысл оценок коэффициентов регрессии, построенной для описания зависимости экспорта Приморского края от инвестиций в портовую инфраструктуру (табл. 3, рис. 2).
Оценка коэффициента регрессии b0 в модели (2) показывает, что при отсутствии инвестиций в порт значение экспорта Приморского края в среднем составит примерно 2272,67 млн руб. При увеличении инвестиций в портовую инфраструктуру на 1 млн руб. значение регионального экспорта в среднем увеличится примерно на 153,309 тыс. руб. Что говорит о наличии прямой линейной взаимосвязи между инвестициями в портовую инфраструктуру и показателем экспорта припортового региона.
Таблица 3
Линейные модели зависимости экспорта от инвестиций в инфраструктуру морских портов
|
Приморский край (2) |
Ленинградская область |
Волгоградская область |
|
|
Вид модели |
Y=А+ВХ |
Y=А+ВХ |
Y=А+ВХ |
|
Переменные |
Coefficient (Std. Error) |
Coefficient (Std. Error) |
Coefficient (Std. Error) |
|
Investment |
0,153309** (0,0533738) |
0,549899*** (0,136345) |
4,34489*** (0,969376) |
|
Constant |
2272,67*** (423,223) |
7019,35*** (1468,30) |
−6760,84*** (1964,64) |
|
R^2 |
0,369293 |
0,309460 |
0,637496 |
|
F-statistic |
8,250478 (0,023911) |
16,26635 (0,003771) |
20,08970 (0,002050) |
Источник: аналитика автора
Примечание:
* соответствует значимости оценки коэффициента при уровне значимости 10%;
** соответствует значимости оценки коэффициента при уровне значимости 5%;
*** соответствует значимости оценки коэффициента при уровне значимости 1%.
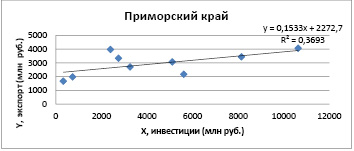
Рис. 2. Поле корреляции и линейный тренд зависимости экспорта Приморского края от инвестиций по данным за 2011-2019 гг.
Источник: аналитика автора
Рассмотрим зависимость численности рабочей силы от инвестиций в развитие портовой инфраструктуры. Считается, что в среднем одна тонна груза в порту приносит 100 долларов добавленной стоимости, а увеличение на один миллион тонн грузов в порту создает дополнительно 300 рабочих мест [11].
Однако, иной характер зависимости демонстрируется при переходе на новый технологический и логистический уровень, когда уменьшение численности рабочей силы в регионе естественно, благодаря повышающемуся уровню инвестиций в портовую инфраструктуру.
Рассмотрим экономическую интерпретацию оценок коэффициентов регрессии в модели зависимости численности рабочей силы Ленинградской области от инвестиций (модель (3), табл. 4, рис. 3).
Оценка коэффициента регрессии b0 в модели (3) показывает, что при отсутствии инвестиций в регион значение численности рабочей силы в среднем составит примерно 962,45 тыс. чел.
При увеличении инвестиций в инфраструктуру портового региона на 1 млн руб. объем его экспорта измениться на (0,0047-4,012e-07(2х+1)) млн руб. Если x0 составляет 3 млрд руб., то при увеличении инвестиций на 1 млн руб. значение регионального экспорта в среднем увеличится примерно на 2,30 тыс. руб.; если x0 составляет 10 млрд руб., то при увеличении инвестиций на 1 млн руб. уменьшение регионального экспорта в среднем составит 3,3 тыс. руб.
Таблица 4
Квадратические модели зависимости численности рабочей силы от инвестиций
|
Ленинградская область (3) |
Волгоградская область |
|
|
Переменные |
Coefficient (Std. Error) |
Coefficient (Std. Error) |
|
Investment |
0,00469671** (0,00184309) |
1,15586* (0,553166) |
|
Investment^2 |
−4,01240e-07** (1,40605e-07) |
−0,000239361* (0,000123119) |
|
Constant |
962,449*** (2,98939) |
−66,4596 (617,844) |
|
R^2 |
0,600730 |
0,745602 |
|
F-statistic |
6,054946 (0,029747) |
7,990806 (0,015596) |
Источник: аналитика автора
Примечание:
* соответствует значимости оценки коэффициента при уровне значимости 10%;
** соответствует значимости оценки коэффициента при уровне значимости 5%;
*** соответствует значимости оценки коэффициента при уровне значимости 1%.
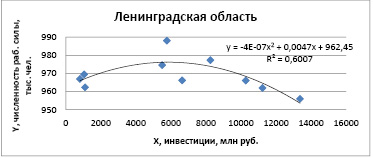
Рис. 3. Поле корреляции и линия квадратичного тренда зависимости численности рабочей силы Ленинградской области от инвестиций по данным за 2010-2019 гг.
Источник: аналитика автора
Для модели (3) координаты точки поворота определяем по формуле нахождения вершины параболы: xверш=5875 млн руб., yверш= 976,26 млн руб.; что соответствует графику, изображенному на рис.3. При прохождении данной точки направление связи между факторным и результативным признаком меняется с роста на снижение. Следовательно, по оцененной модели при росте инвестиций до 5875 млн руб. численность рабочей силы в регионе увеличивается, с дальнейшим ростом инвестиций ее значения уменьшаются.
Такая зависимость означает, что переход на новый технологический вместе с внедрением инновационных технологий и развитием сферы логистических услуг дает уменьшение количества задействованной рабочей силы в рассматриваемом регионе.
Заключение
В работе выявлена статистически значимая взаимосвязь между социально-экономическими показателями и инвестициями в портовую инфраструктуру группы регионов РФ, прилежащих к пяти морским портам РФ. Зависимости социально-экономических показателей от инвестиций в портовую инфраструктуру различаются в зависимости от региона. Интерпретация экономического смысла оценок коэффициентов регрессии для построенных моделей дает более полное описание характера выявленной зависимости. Для приведенных в работе квадратических моделей регрессии составлен комплексный экономический смысл оценок коэффициентов регрессии. Полученные результаты могут быть использованы при исследовании влияния инвестиций на социально-экономические показатели портовых регионов и для их прогнозирования.
Работа выполнена при финансовой поддержке гранта РФФИ № 19-510-23001 в рамках конкурса на лучшие научные проекты фундаментальных исследований, проводимый совместно РФФИ и Фондом «За русский язык и культуру» в Венгрии.

