Введение
Эта статья – вторая, продолжающая цикл работ д.э.н., профессора кафедры математических методов в экономике РЭУ им. Г.В. Плеханова Халикова Михаила Альфредовича и соискателя по этой кафедре Аббясовой Дианы Рустямовны. Напомним, что в первой публикации по тематике оптимального управления производственным сегментом компании с долгом авторы рассматривали особенности реализации ее дивидендной политики в условиях ограниченного и, напротив, расширенного доступа к внешним источникам финансирования рыночной деятельности. В этой публикации основное внимание уделяется оценке значимости факторов стоимости такой компании и влияния на стоимость реализуемых инвестиционных проектов модернизации и расширения производства.
Цель статьи – разработка теоретической базы анализа и управления факторами стоимости операционного сегмента компании с долгом, обоснования постановки задачи и модели выбора приоритетного набора инвестиционных проектов модернизации и расширения производства с критериями стоимости генерируемых в этом сегменте денежных потоков, производственными и ресурсными ограничениями, а также ограничением на риск структуры привлекаемого в проекты капитала.
Материалы и методы исследования
Настоящая статья является продолжением исследований проф. М.А. Халикова и его учеников по тематике оценки эффективности и риска производственного сегмента предприятия акционерной формы собственности, что предполагает широкое цитирование работ предшественников по этой и сопряженной с ней тематикам. В частности: авторов неоклассической производственной теории: Г.Б. Клейнера [10,11], Р. Дорфмана, П. Самуэльсона и Р. Солоу [16,20,21]. Необходимо также подчеркнуть определенную связь изложенного материала с работами Д.А. Безухова [2], М.А. Бендикова [3], М.А. Горского [4, 5, 6, 7, 8, 9, 19], Б. Коласса [12], М. Круи [13], Е.М. Решульской [19], Ф. Турино [18], И.Э. Фролова [3], Ю.Е. Хрусталева [15], посвященными повышению эффективности и устойчивости высокотехнологичных предприятий и холдинг-компаний. Математический аппарат для последующих расчетов по модели выбора приоритетного набора инвестиционных проектов предполагается организовать на основе авторских разработок с использованием методов, заимствованных из работ Н.П. Бахвалова [1], А.С. Хасанова [14] и Д. Лиенберга [17].
Результаты исследования и их обсуждение
I. Стоимость и доходность компании без долга и с долгом.
1) Случай компании без долга. Во временном интервале t1 сделали инвестицию размером I, причем все вложения являются собственным. Тогда в интервале t2 > t1 получим бессрочный поток ренты величиной 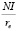 , где NI – посленалоговая прибыль:
, где NI – посленалоговая прибыль:
NI = (V – Z) · (1 – NP),
где V и Z, соответственно, операционный доход и операционные затраты, NP – налог на прибыль, re – стоимость собственного капитала, рассчитанная на рассматриваемый временной интервал например, по модели САРМ.
Тогда стоимость компании в точке t2 оценивается свободным потоком ренты 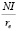 , а стоимость в точке t1 составит:
, а стоимость в точке t1 составит:
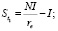 (1)
(1)
Доходность ДБ.Д. акционеров компании без долга, учитывая полный расчет по налогам составит 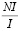 или, что то же самое:
или, что то же самое:
ДБ.Д. 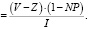 (2)
(2)
Для базы сравнения доходности акционеров полезно использовать рентабельность собственного капитала. Если ren – минимально допустимый уровень рентабельности собственного капитала, то справедливо соотношение:
ДБ.Д. ≥ ren или 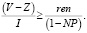 (3)
(3)
Таким образом, для компании без долга доходность акционеров ограничена рентабельностью собственного капитала и может быть увеличена вместе с налоговым щитом величиной (1 – NP).
2) Рассмотрим случай, когда компания поддерживает постоянный уровень долга величиной (1 – kA)% от величины I первоначальной инвестиции (kA – коэффициент автономии).
Пусть инвестиция I, в которой стоимость долга составляет I · (1 – kA) · rD · (1 – NP) (rD – эффективная ставка по кредиту, NP – налог на прибыль), позволяет генерировать прибыль объемом
NI = (VD – Zat –I · (1 – kA) · rD) · (1 – NP).
Учитывая, что кредитор получает в точке t1 первоначальной инвестиции бесконечную ренту объемом 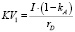 , а в точке t2 произошла «расплата» за кредит, то стоимость компании в этой точке определяется бессрочной рентой на собственный капитал:
, а в точке t2 произошла «расплата» за кредит, то стоимость компании в этой точке определяется бессрочной рентой на собственный капитал:
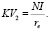 (4)
(4)
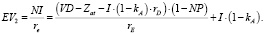 (5)
(5)
Определим доходность акционерного капитала компании с долгом:
ДС.Д. 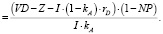 (6)
(6)
Особый интерес представляет случай более высокой стоимости компании с долгом:
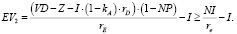 (7)
(7)
или
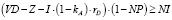
и (или) доходности акционерного капитала:
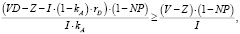
что обеспечивается в случае, если:
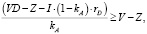
или
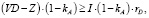
или
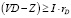 ,
,
или
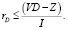 (8)
(8)
Таким образом, доказано утверждение:
Утверждение 1. Справедливая доходность акционерного капитала компании с долгом принимает максимальное значение в случае, если эффективная ставка rD по кредиту, объем первоначальной инвестиции I и прибыль операционного сегмента предприятия удовлетворяют соотношению:
(VD – Z) ≥ I ∙ rD.
II. Оценка влияния факторов стоимости компании с долгом.
Вернемся к формуле (7) оценки стоимости компании с долгом в точке t = t2:
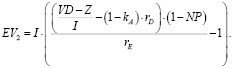 (7’)
(7’)
Напомним, что первоначальная инвестиция I, в которой I · (1 – kA) – заемный капитал, взятый под эффективный процент rD.
Тогда EBT = EBIT – (1 – kA) · rD и прибыль 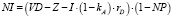 .
.
Стоимость 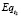 собственного капитала в точке t2 составит:
собственного капитала в точке t2 составит:
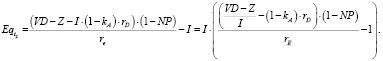 (7’’)
(7’’)
Учитывая, что
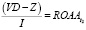
(рентабельность рабочих активов в точке t2), можно сделать вывод о справедливости утверждения:
Утверждение2. Компания с долгом увеличивает стоимость собственного капитала, если выполняется базовое условие:
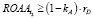
(рентабельность активов в точке расчета стоимости компании как минимум покрывает затраты на заемный капитал).
В этом случае стоимость компании прямо пропорциональна первоначальной инвестиции и рентабельности рабочих активов.
III. Постановка задачи управления стоимостью операционного сегмента компании на этапах реализации проектов технического перевооружения производства.
Пусть проекты Prj пронумерованы индексом 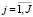 ; Prj – объем планируемых инвестиций в j-й проект;
; Prj – объем планируемых инвестиций в j-й проект; 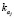 – планируемая доля собственного финансирования j-го проекта; rD – ставка заемного финансирования j-го проекта; ROAAj – предполагаемая рентабельность j-го проекта.
– планируемая доля собственного финансирования j-го проекта; rD – ставка заемного финансирования j-го проекта; ROAAj – предполагаемая рентабельность j-го проекта.
Тогда модель выбора оптимальной последовательности проектов технического перевооружения операционного сегмента предприятия для очередного шага 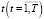 включает критерий:
включает критерий:
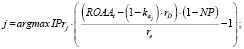 (7’’’)
(7’’’)
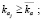 (8)
(8)
ограничения на финансовую и материально-технологическую реализуемость проекта и решается на двух уровнях.
Задача верхнего уровня связана с выбором набора реализуемых инвестиционных проектов, исходя из следующей информации: 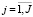 – индекс проекта; ROAAj – рентабельность j-го проекта; Prj – первоначальная (стартовая) инвестиция в j-й проект; OR – общее финансовое обеспечение инвестиционной деятельности предприятия (собственные и планируемые заемные средства);
– индекс проекта; ROAAj – рентабельность j-го проекта; Prj – первоначальная (стартовая) инвестиция в j-й проект; OR – общее финансовое обеспечение инвестиционной деятельности предприятия (собственные и планируемые заемные средства); 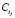 – затраты i-го актива (постоянного или переменного) на реализацию j-го проекта; Ci – учитываемый в инвестиционной деятельности операционного сегмента предприятия объем i-го актива (i= 1,I);
– затраты i-го актива (постоянного или переменного) на реализацию j-го проекта; Ci – учитываемый в инвестиционной деятельности операционного сегмента предприятия объем i-го актива (i= 1,I);
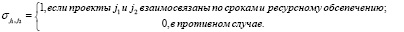
В постановочном плане задаче верхнего уровня – задача булева программирования (относится к классу задач «о рюкзаке»):
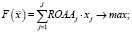 (9)
(9)
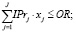 (10)
(10)
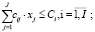 (11)
(11)
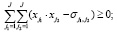 (12)
(12)
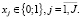 (13)
(13)
Задача нижнего уровня связана с определением структуры капитала для каждого из выбранных на верхнем уровне проектов (j = 1, … J1) с критерием на стоимость операционного сегмента предприятия с долгом и ограничением на средневзвешенные затраты на капитал проекта:
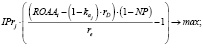
(14)
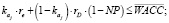 (15)
(15)
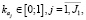 (16)
(16)
где 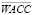 – ограничение на средневзвешенную стоимость капитала реализуемых проектов.
– ограничение на средневзвешенную стоимость капитала реализуемых проектов.
Учитывая нелинейный характер зависимости в паре «ставка rD по кредиту – коэффициент 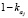 финансовой зависимости», можно утверждать о принадлежности задачи (14)-(16) к нелинейным выпуклым задачам, для которых разработаны эффективные алгоритмы решения, отмеченные в цитируемых выше источниках (в частности, [1, 5, 6, 14, 17]).
финансовой зависимости», можно утверждать о принадлежности задачи (14)-(16) к нелинейным выпуклым задачам, для которых разработаны эффективные алгоритмы решения, отмеченные в цитируемых выше источниках (в частности, [1, 5, 6, 14, 17]).
Заключение
Обобщая совокупность полученных выше результатов, констатируем, что поставленная в преамбуле цель, связанная с разработкой теоретической базы анализа и управления факторами стоимости операционного сегмента компании с долгом достигнута, авторами обоснована постановка задачи и построены модели выбора приоритетного набора инвестиционных проектов модернизации и расширения операционного сегмента предприятия с критериями стоимости генерируемых в нем денежных потоков, производственными и ресурсными ограничениями, а также ограничением на риск структуры привлекаемого в проекты капитала.

