Введение
Задача кредитного скоринга является важнейшей составляющей процесса кредитования в банковской сфере. На основе результатов моделей кредитного скоринга, среди прочего, рассчитывается средний уровень вероятности дефолта (Probability of Default – PD) – одного из факторов, участвующих в расчете норматива достаточности капитала в соответствии с требованиями Базельского комитета [1] в рамках продвинутого подхода на основе внутренних рейтингов (A-IRB). Модель напрямую влияет на предсказанные значения долгосрочной вероятности дефолта, что может приводить к существенным изменениям требований к резервному капиталу банка.
Перед банками стоит задача построения высококачественной модели для решения задачи кредитного скоринга, так как это позволит, во-первых, сократить объемы резервов по требованиям Центрального Банка, во-вторых, более качественно определять вероятность невозврата кредита на уровне отдельного заемщика, и, в-третьих, ранжировать пулы клиентов по величине риска для формирования кредитного портфеля.
Одной из важнейших составляющих задач кредитного скоринга является способность ранжирующего алгоритма выполнять сегментацию клиентов. Интерпретируемая сегментация на платежеспособных и неплатежеспособных заемщиков является конечным результатом, в то время как неинтерпретируемая сегментация в пространстве латентных признаков может быть более ценной с точки зрения ранжирующей способности финальной модели ранжирования заемщиков. Под латентными признаками можно понимать некоторую комбинацию исходных признаков заемщика. Выделяемые сегменты используются либо в качестве предиктора в моделях машинного обучения любой сложности, либо в качестве разделителя портфеля клиентов. Они позволяют оценивать параметры отдельной модели для каждого сегмента, что улучшает качество кредитного скоринга по сравнению с использованием единой модели для всего портфеля заемщиков.
Введем некоторые понятия, которые будут использованы в дальнейшем. В работе рассматриваются нейросетевые методы глубокого обучения (Deep Learning) для выделения скрытых клиентских сегментов в латентном пространстве признаков. Латентное признаковое пространство можно представить в виде результата применения некоторой функции к аффинной трансформации входов в нейронную сеть. Данная функция реализует нелинейное преобразование матрицы исходных параметров в сжатую матрицу латентных признаков, характеризующих заемщиков:
f (WX + b),
где X – вектор-строка размерности 1 × n, где n – число признаков, характеризующих каждого заемщика,
W – вектор-столбец коэффициентов размерности 1 × n для каждого из характеризующих признаков,
b – скаляр, характеризующий свободный член модели (bias).
Количество таких преобразований тем больше, чем «глубже» нейронная сеть, т.е. чем больше скрытых слоев она содержит. Отметим, что латентные признаки не обладают свойством экономической интерпретируемости, в отличие от исходных признаков. Более подробно это рассматривается в п. 2.2.
Автокодировщиком называется нейронная сеть, содержащая, как минимум, 1 скрытый слой. Особенность данной нейронной сети заключается в унификации – вход и выход автокодировщика эквивалентны, искомый результат применения данной модели состоит в признаковом представлении на уровне скрытого слоя. Более подробно использование автокодировщиков рассмотрено в п.2.2.
Качество ранжирующей способности модели кредитного скоринга характеризуется коэффициентом Джини [8]. На рассмотренном наборе данных заемщиков – юридических лиц удалось повысить коэффициент Джини на 3% и 8% при использовании сегментационных моделей на основе многослойного перцептрона и автокодировщика соответственно.
Многослойный перцептрон и автокодировщик традиционно используются в сфере анализа изображений, аудио- и видеосигналов. Обобщение данного подхода в сферу задач кредитного скоринга генерирует дополнительную полезность в терминах метрики качества Джини.
Нейросетевые модели для выделения сегментов в латентном признаковом пространстве
Рассмотрим 2 варианта нейросетевых архитектур, скрытые слои которых могут быть использованы для формирования латентного признакового пространства.
1. Полносвязная нейронная сеть (многослойный перцептрон)
Многослойный перцептрон является модификацией оригинального перцептрона Розенблатта, предложенного в 1958-м году [2]. Данный перцептрон может состоять из одного или более скрытых слоев нейронов между входным и выходными слоями (рис. 1). Число входных нейронов соответствует числу признаков заемщика, а число нейронов в выходном слое равно числу классов соответствующей задачи классификации (в простейшем случае для кредитного скоринга число классов равно 2, дефолт/не-дефолт). Каждый нейрон в скрытых слоях является результатом трансформации WX, выход каждого нейрона – результат применения некоторой нелинейной функции активации к нейрону скрытого слоя – f (WX).
2. Автокодировщик (autoencoder)
Наиболее распространенной моделью глубокого обучения для извлечения латентных признаков является автокодировщик [9].
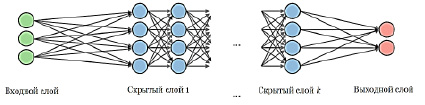
Рис. 1. Графическое представление типовой архитектуры МСП [4]
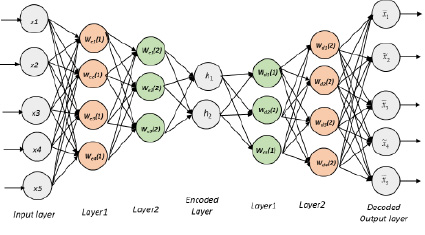
Рис. 2. Графическое представление типовой архитектуры автокодировщика
Являясь примером модели для решения задач класса обучения без учителя (unsupervised learning), автокодировщик характеризуется структурой (рис. 2), которая позволяет сокращать признаковое описание объекта за счет следующей архитектуры сети:
Автокодировщик (autoencoder) является полносвязной нейронной сетью, которая обучается реконструировать входные данные. В автокодировщике, в отличие от многослойного перцептрона, используются два семейства функций, первое решает задачу уменьшения количества признаков заемщика, а второе – задачу увеличения количества признаков до исходного. Это позволяет получить латентное признаковое описание в скрытых слоях сети, которое меньшим количеством параметров характеризует заемщика.
Автокодировщик моделирует не событие дефолт/не-дефолт, связанное с конкретным заемщиком, а признаковое описание заемщика.
Приведем аналогию использования автокодировщика для анализа изображений. Автокодировщик, пропуская набор входных пикселов через внутреннюю структуру, получает на выходе видоизмененное изображение, которое, однако, должно быть максимально похожим на исходное. На внутреннем слое автокодировщика происходит существенное снижение числа пикселов изображения. Это означает, что достаточно меньшего числа пикселей, чтобы уловить основные характеристики изображения (контуры, объекты и т.д.). Достигается это за счет параллельного обучения т.н. генератора и дискриминатора, генератор решает задачу генерации конкретного объекта на основе его сокращенного признакового описания, а дискриминатор оценивает, насколько полученный объект далек от исходного в смысле некоторой меры близости.
Рассмотрим логику работы автокодировщика на примере задачи кредитного скоринга. Генератор в данном случае будет пытаться воссоздать исходный объект, находящийся в обучающей выборке в смысле набора заданных признаков – табл. 1. Здесь строками являются наблюдения в выборке (заемщики банка), а столбцами – признаки, которыми описываются эти заемщики. В классической постановке задачи кредитного скоринга данные признаки используются как предикторы в модели логистической регрессии для оценки вероятности дефолта.
Таблица 1
Пример автокодировщика для кредитного скоринга
|
ID Заемщика |
Сумма кредита |
ROE |
Прибыль 12 мес. |
EBITDA |
ЛатПр_1 |
ЛатПр_2 |
ЛатПр_3 |
… |
|
00001 |
… |
… |
… |
… |
… |
… |
… |
… |
|
00002 |
… |
… |
… |
… |
… |
… |
… |
… |
|
… |
… |
… |
… |
… |
… |
… |
… |
… |
Все рассматриваемые признаки, таким образом, имеют экономический смысл, связанный с конкретным заемщиком. После применения автокодировщика признаковое пространство сжимается, как показано на рис. 2, в слое «Encoded layer», в частности, оно достигает минимального числа признаков. Именно эти признаки из сжатого пространства представляется целесообразным добавить к исходному набору факторов для построения модели вероятности дефолта. Признаки, добавленные из скрытого слоя автокодировщика, обозначены в табл. 1 как «ЛатПр_1» (Латентный Признак), «ЛатПр_2» и т.д.
Следующие слои автокодировщика, наоборот, расширяют признаковое пространство до исходного количества, восстанавливая каждый объект наблюдения. Точного совпадения не получается, однако это и не требуется, т.к. цель применения данной архитектуры на данном этапе анализа достигнута – получен новый набор латентных признаков.
Отметим, что латентные признаки не обладают теми же свойствами интерпретируемости исходных признаков, т.к. генерируются с помощью применения нескольких нелинейных функций ко всему набору исходных признаков.
Алгоритм обучения нейросетевых архитектур для задачи бинарной классификации заемщиков
Обучение нейронных сетей включает следующие этапы:
1. Определяется тип решаемой задачи (бинарная классификация в случае задачи кредитного скоринга)
2. Выбирается функция потерь J(θ), где θ – набор параметров модели бинарной классификации заемщиков. Функция потерь используется для вычисления оптимального набора параметров – для нее решается задача минимизации по θ. В данной работе использовалась следующая функция потерь [10]:
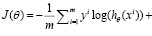
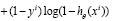 ,
,
где j – функция потерь;
θ – вектор весовых коэффициентов при факторах модели;
m – размер выборки;
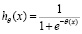 – вероятность принадлежности объекта к классу с меткой 1;
– вероятность принадлежности объекта к классу с меткой 1;
i – порядковый номер наблюдения;
Целевое событие связано с факторами следующим образом:
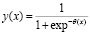 ,
,
где y(x) – вероятность дефолта заемщика
x – набор факторов.
3. Решается оптимизационная задача (либо аналитическим методом, либо с помощью численной оптимизации), определяется оптимальный вектор θ.
4. По полученным в процессе оптимизации весовым коэффициентам θ рассчитывается вероятность дефолта заемщиков y(x). Качество прогноза модели оценивается на тестовой выборке заемщиков.
Под обучением понимается подбор оптимальных с точки зрения заданной функции потерь параметров сети W, связывающих нейроны между собой. На каждом слое производится аффинная трансформация, после чего применяется одна из нелинейных функций активации. Именно значения векторов, характеризующих заемщиков, после активации используются в качестве латентных признаков для определения скрытых сегментов среди клиентов банка.
Наиболее распространенные функции активации представлены на рисунке 3.
В рамках данной работы для всех экспериментов использовалась функция активации ReLU (Rectified Linear Unit) (рис. 3с), так как во многих прикладных задачах она показала свою эффективность [11].
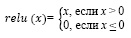
Для обучения нейросетевых моделей, представленных выше, используется алгоритм обратного распространения ошибки (backpropagation). При использовании нейронной сети прямого распространения, которая принимает вход х и порождает выход y, информация передается по сети в одном направлении – вперед. Вход х содержит начальную информацию, которая доходит до скрытых блоков каждого слоя – это называется прямым распространением. На этапе обучения прямое распространение может продолжаться, пока не будет получена оценка функции потерь J(θ). Алгоритм обратного распространения [3] позволяет передавать информацию о функции потерь назад по сети для вычисления градиента функции потерь по вектору признаков [4].
Подробное описание алгоритма обучения с помощью обратного распространения ошибки представлено в [4].
Идея кредитного скоринга на основе скрытых сегментов состоит в идентификации данных сегментов, каждый из которых должен различаться по уровню риска оказавшихся в нем клиентов. Эндогенные переменные, определяющие вероятность заемщика оказаться неплатежеспособным, могут варьироваться от сегмента к сегменту. Анализ межсегментных различий позволяет предположить, что построение отдельных моделей кредитного скоринга для каждого сегмента может привести к увеличению общего качества предсказания дефолта.
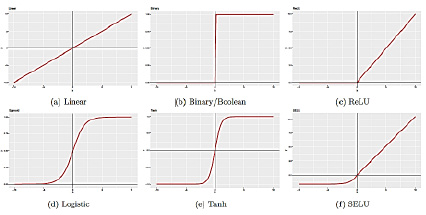
Рис. 3. Графики некоторых функций активации [4]
Под моделью кредитного скоринга в данном случае понимается классическая для банков модель логистической регрессии над набором факторов. Для чистоты эксперимента набор факторов фиксирован и не меняется от сегмента к сегменту. Таким образом возможно оценить чистый эффект от применения нейросетевых архитектур, выделяющих сегменты в латентном признаковом пространстве.
Задача кредитного скоринга рассматривается как частный случай задачи бинарной классификации, в которой целевое событие – факт реализации дефолта. Факт дефолта определяется следующим образом:
• заемщик признается находящимся в дефолте, если суммарная длительность просроченных платежей по его кредитным обязательствам превышает 90 дней в течение 18 месяцев с начала наблюдения;
• заемщик признается не находящимся в дефолте, если в течение 18 месяцев с начала наблюдения для него не было зафиксировано суммарных просрочек платежей по кредитным обязательствам, превышающих 90 дней.
Метрикой качества алгоритмов принимается коэффициент Джини [5], который непосредственно связан с CAP-кривой (Cumulative Accuracy Profile) [6].
CAP-кривая показывает, какой части дефолтных клиентов модель присваивает относительно худший скоринговый балл. Соответствующий CAP-кривой коэффициент Джини (Gini) вычисляется следующим образом:
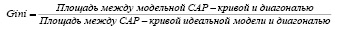
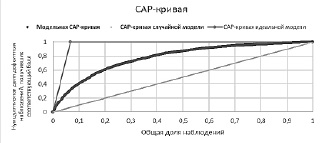
Рис. 4. Пример CAP-кривой
Коэффициент Джини варьируется в интервале [0, 1], где 1 – идеальная модель, 0 – случайные результаты (аналогичные подбрасыванию монеты).
Эксперименты и результаты
В качестве исходных данных использовалась выборка кредитных заявок крупнейших банков России, относящиеся к сегменту «Малый бизнес (ИП и ООО)». Список влияющих факторов для оценивания параметров логистической регрессии (непосредственно задача кредитного скоринга) включает как данные из кредитной анкеты (срок кредита, сумма кредита, максимальное число дней просрочки по кредитам за последние 2 года, число собственников и т.д.), так и финансовые показатели (среднемесячная прибыль за последний год, среднемесячные операционные расходы за последний год, ROE и т.д.). Общее количество учтенных факторов составило 47 (28 факторов на основе кредитной заявки и 19 факторов на основе финансовых показателей). Временной горизонт для выборки составил 36 мес.
Для решения задачи сегментации на основе нейросетевых архитектур дополнительно использовались данные транзакций клиентов – было сформировано 30 факторов-агрегатов (средняя сумма транзакций за последние 3 мес., среднее число транзакций за последние 3 мес. и т.д.)
Для тестирования предлагаемых нейросетевых методов сегментации использовался следующий алгоритм:
1. Все имеющиеся данные используются для обучения соответствующей модели (для МСП решается задача обучения с учителем, для автокодировщика – без учителя).
2. На основе обученных моделей производится извлечение признаков из латентного признакового пространства – для МСП латентными признаками являются активации предпоследнего слоя нейронной сети (10 нейронов), для автокодировщика – нейроны, находящиеся в encoder слое (рис. 2) (аналогично, 10 нейронов).
3. С помощью простого алгоритма K-средних [7] в извлеченном признаковом пространстве определяются 3 кластера клиентов, максимально отдаленных друг от друга.
4. Для каждого полученного сегмента строится модель кредитного скоринга на основе полного набора факторов с помощью алгоритма логистической регрессии
5. Оценивается эффект от использования сегментации расчетом коэффициента Джини и сравнением Джини для каждого сегмента с Джини модели, построенной на всем наборе данных.
Отметим, что число нейронов, используемое для определения скрытого признакового пространства, является фиксированным, как и число сегментов, выделяемое на этапе применения K-средних. Для определения наилучшей комбинации данных параметров требуется существенное расширение объема выборки заемщиков.
Ниже приведена информация по числу наблюдений в выборке до/после сегментации, а также уровни риска (Default Rate) на уровне всей выборки и на уровне полученных сегментов (табл. 2, 3).
Таблица 2
Дескриптивные статистики выборки для сегментатора-МСП
|
Алгоритм сегментации |
Data |
% от всей выборки |
Число наблюдений |
Число дефолтов |
DR, % |
|
Многослойный перцептрон (МСП) |
Сегмент 1 |
36 |
51 523 |
3 762 |
7,30 |
|
Сегмент 2 |
34 |
49 123 |
3 021 |
6,15 |
|
|
Сегмент 3 |
29 |
41 776 |
2 848 |
6,82 |
|
|
Итого |
100 |
142 422 |
9 631 |
6,76 |
Таблица 3
Дескриптивные статистики для выборки сегментатора-автокодировщика
|
Алгоритм сегментации |
Data |
% от всей выборки |
Число наблюдений |
Число дефолтов |
DR, % |
|
Автокодировщик |
Сегмент 1 |
48 |
68 363 |
1 926 |
2,82 |
|
Сегмент 2 |
29 |
41 302 |
2 718 |
6,58 |
|
|
Сегмент 3 |
23 |
32 757 |
4 987 |
15,22 |
|
|
Итого |
100 |
142 422 |
9 631 |
6,76 |
Таблица 4
Итоговые результаты
|
Сегмент |
Коэффициент Джини средний |
Коэффициент Джини в разбивке по сегментам |
|
Вся выборка (без сегментации) |
51,58% |
--- |
|
Сегментация МСП |
54,35% |
50,27% |
|
52,94% |
||
|
59,84% |
||
|
Сегментация автокодировщиком |
59,81% |
54,76% |
|
58,49% |
||
|
66,19% |
При использовании автокодировщика полученные 3 сегмента легко поддаются интерпретации с точки зрения риска – к первому сегменту (самому многочисленному) относятся платежеспособные заемщики, ко второму – потенциально проблемные клиенты, и к третьему – наиболее рискованные заемщики.
Кредитный скоринг решает ту же задачу – разнесение клиентов по группам, однородным по уровню риска. Чтобы убедиться в том, что предлагаемые нейросетевые методы генерируют дополнительную полезность в процесс принятия решения по выдаче кредита клиенту, проведем этапы 4 и 5 предлагаемого алгоритма. Результаты представлены в таблице 4.
Полученные результаты подтвердили перспективность использования методов глубокого обучения для улучшения качества моделей, использующихся в рамках кредитного скоринга.

