Научный журнал

Вестник Алтайской академии экономики и права

Print ISSN 1818-4057

Online ISSN 2226-3977

Перечень ВАК

Введение

Эта публикация является прямым продолжением исследований профессора М.А. Халикова и его учеников по проблематике динамической оптимизации производственной сферы предприятия с критериями эффективности и рентабельности затрат, финансируемых из собственных и заемных источников и с ограничениями, включающими и ограничение на риск структуры пассивов рабочего капитала. В первую очередь, здесь следует процитировать работы указанного коллектива авторов [1,3-6,11], отметив, что предлагаемая в статье постановка задачи динамической оптимизации является оригинальной в плане выбранного объекта приложения – рассматривается вариант предприятия, зависимость в паре «затраты-выпуск» которого корректно описывается неоклассической производственной функцией [9].

Материалы и методы исследования

Методологическую основу исследования составили работы отечественных и зарубежных учёных по:

1) проблемам моделирования производственной сферы предприятия в условиях неопределенности и риска [12,17];

2) оптимизации социально-экономических систем на микроуровне [2,8];

3) методам дискретной оптимизации в непрерывной и дискретной постановках [14-16];

4) методам оценки и учета в моделях производственной сферы предприятия внешних и внутренних рисков [13,15].

Цель исследования – продолжение исследований, начатых в публикациях [3-5] и связанных с разработкой экономико-математического инструментария моделей и методов выбора оптимальных по экономическому критерию вариантов управления денежными и материальными потоками производственной сферы предприятия в части разработки и адаптации постановок задач и алгоритмов их динамической оптимизации на выбранном плановом горизонте.

Результаты исследования и их обсуждение

1. Производственная сфера предприятия и метод динамического моделирования ее денежных потоков.

Объектом исследований в этой статье является производственная сфера рыночной деятельности корпорации (предприятия частной формы собственности), в рамках которой осуществляются планирование и организация основного производственного процесса, снабжение, подготовка производства и сбыт (реализация) готовой продукции.

Целью производственной деятельности является получение эффекта в виде прибыли или другого дохода от активов производственной сферы, используемых в технологическом процессе.

Активы производственной сферы предприятия (в совокупности образуют рабочий капитал) по способу списания на затраты производственной деятельности подразделяются на постоянные и переменные.

Пассивы рабочего капитала формируются из собственных средств, производственного сегмента предприятия и заемных, привлекаемых из внешних источников (на платной основе) на покрытие прямых и косвенных производственных затрат.

Основой моделирования производственного сегмента предприятия является производственная функция, в аналитической или табличной форме связывающая выпуск продукции в натуральном или стоимостном выражении (стоимость «на выходе») с затратами активов рабочего капитала, используемых в технологическом процессе ее производства (стоимость «на входе»). В частности, в работе используется аналитическое выражение для неоклассической производственной функции, а также основные ее свойства, связанные с интерпретацией коэффициента однородности (эти данные заимствованы из работ Б.Г. Клейнера и М.А. Халикова) [1,9].

Приведем основные соотношения динамической модели производственной сферы предприятия, связывающие активы и пассивы, включаемые в рабочий капитал на последовательных временных интервалах t–1 (предыдущий) и t (текущий), где t ∈ 0,T (T – горизонт планирования):

1) PKt = PKt–1 , (1)

т.е рабочий капитал производственной сферы на начало текущего временного интервала совпадает по величине и составляющим с рабочим капиталом на конец предыдущего временного интервала;

2) PKt = (1 – σ) × PKt + γt × yt , (2)

рабочий капитал (в части активов) на конец временного интервала t образуется из рабочего капитала на начало этого временного интервала (за исключением амортизируемой доли) и собственных инвестиций предприятия, и валовой прибыли yt периода t (γt – доля собственных инвестиций в рабочий капитал для периода t);

3) yt = (1 – τ) (pt × yt – wt – (1 + ρt) × ЗKt), (3)

где τ – налог на прибыль; pt – цена реализации произведенной в периоде t продукции объемом yt; wt – нормируемые постоянные и переменные затраты на выпуск продукции объемом yt; ρt – ставка краткосрочного кредита объемом ЗKt в пассивах рабочего капитала производственной сферы предприятия для периода t.

Объем yt производства для периода t не может превышать прогнозируемого спроса SPt на продукцию предприятия для этого периода и его производственной мощности, ограниченной постоянными и переменными активами рабочего капитала PKt на начало временного интервала t. Напомним, что для предприятия с неоклассической производственной функцией справедливо:

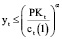, (4)

где ct(1) – удельные затраты на производство продукции для временного интервала t; α – степень однородности производственной функции предприятия.

Таким образом, для yt справедливо:

4) 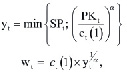(5)

(6)

где wt – oтмеченные в соотношении (3) полные затраты производственной сферы предприятия для временного интервала t;

5) ЗKt = PKt × (1 – kt), (7)

где kt – коэффициент автономии структуры пассивов рабочего капитала предприятия, выбранный для временного интервала t (отношение собственного капитала PKt производственной сферы к полному капиталу PKt + ЗKt);

6) Dt = (1 – γt) × yt , (8)

где Dt – объем средств из валовой прибыли производственной сферы предприятия для временного интервала t, выделяемые на непроизводственное потребление (в частности, на выплату дивидендов).

Приведенные соотношения (1) – (8) в совокупности описывают баланс денежных и материальных потоков производственной сферы предприятия на временных интервалах t (t = 1,T).

В таблице 1 представим описание используемых в этих соотношениях экзогенных (неуправляемых) и эндогенных (управляемых) параметров.

Таким образом, балансы денежных и материальных потоков производственной сферы предприятия для временного интервала t (t = 1,T), задаются соотношениями (2) – (8), а переход от одного временного интервала к другому соотношением (1).

Манипулируя параметрами kt и γt (соответственно коэффициент автономии структуры пассива рабочего капитала производственной сферы и доля отчислений из прибыли на инвестиции в рабочий капитал), можно ставить и решать следующие задачи оптимального управления производственным сегментом предприятия:

а) максимально увеличить производственную мощность (объем рабочего капитала) и выпуск продукции к концу планового периода Т) в условиях прогнозируемых интервалов измерения рыночного спроса и цен на продукцию и с учетом выбранных нормативов на риск структуры рабочего капитала (коэффициент автономии к концу планового периода Т, а также на промежуточных временных интервалах не должен быть меньше предельного значения);

б) максимально повысить инвестиционную привлекательность производственного сегмента предприятия к концу планового периода Т в условиях прогнозируемых интервалов изменения рыночного спроса и цен на продукцию путем увеличения дивидендных выплат с учетом пороговых значений рентабельности активов рабочего капитала и риска его структуры;

Таблица 1

Экзогенные и эндогенные параметры динамической модели производственной сферы предприятия

в) максимально повысить рентабельность рабочего капитала производственной сферы предприятия к концу планового периода Т в условиях прогнозируемых интервалов изменения рыночных спроса и цен на продукцию с учетом пороговых значений риска структуры рабочего капитала и доли отчислений из прибыли на непроизводственное потребление.

Перечисленные постановки задач, конечно же, не исчерпывают поле решаемых проблем управления материальными и денежными потоками производственной сферы хозяйствующего в рыночной экономике предприятия. Однако по содержанию и элементному наполнению перечисленные задачи весьма актуальны с практической точки зрения, и возможности эмпирических исследований на основе построенных формализованных моделей.

Рассмотрим эти модели.

• Модель задачи п. а), кроме соотношений (1)-(8), включает ограничения:

- на прогнозируемые интервалы изменения рыночных спроса и цен реализации продукции предприятия:

SPt ∈ [Sp; Sp], pt ∈ [p; p] , (9)

где в ограничениях указаны соответственно нижние и верхние границы прогнозируемых интервалов изменения спроса и цен;

- на максимальный риск структуры пассивов рабочего капитала:

kt ≤ k, t = 1,T (10)

Критерий задачи п а):

max yt , (11)

Таким образом, задачи п. а) корректно описывается системой выражений (1)–(11).

• Модель задачи в), кроме соотношений (1)–(8), включает ограничения (9), (10) и ограничение на минимальный уровень рентабельности активов рабочего капитала на всем плановом горизонте t = [1; T]:

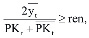(12)

где ren – порог рентабельности средней за временной интервал t величины активов рабочего капитала производственной сферы предприятия.

Критерий задачи – максимум отчислений на непроизводственное потребление к концу периода планового периода Т:

Dt → max, (13)

Таким образом, модель задачи в) описывается системой выражений (1)–(10), (12), (13).

• Модель задачи с), кроме соотношений (1)–(8), также включает ограничения (9), (10) и ограничение на нижний порог доли отчислений на непроизводственное потребление:

1 – γt ≥ Liv, (14)

где Liv – нижний порог доли дивидендных выплат из прибыли производственной сферы предприятия.

Критерий этой задачи – максимум рентабельности активов рабочего капитала производственного сегмента предприятия к концу планового периода Т:

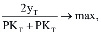(15)

2. Эмпирические расчеты динамики производственной сферы предприятия с критерием (11).

Исследования экономической динамики производственной сферы предприятия, функционирующего на конкурентных товарных, ресурсных и финансовых рынков и для частного случая линейной зависимости в паре «затраты-выпуск» (степень однородности производственной функции α = 1), проводились М.А. Халиковым и его учениками: А.М. Антиколь, Э.А. Бабаян, Р.М. Расуловым и Д.А. Безуховым [1,3-5].

Авторами показано, что в этом случае экономическая динамика предприятия корректно описывается однородными разностными уравнениями второго порядка. Если соответствующее характеристическое уравнение разрешимо в действительных числах, то динамика выпуска описывается возрастающей или убывающей экспоненциальной функцией, если в комплексных, то – периодической волнообразной функцией (растущей или затухающей).

Для исследования экономической динамики предприятия с нелинейной неоклассической производственной функцией, задаваемой уравнениями (1)–(11), предлагается рассмотреть случаи растущей (α > 1) и падающей (α < 1) отдачи от масштаба производства.

Не ограничивая общности рассуждений, будем считать фиксированными: ставку τ налогообложения прибыли, цены р – товарного и ρ – финансового рынков, а также технологические константы: с(1) (удельные затраты) и PK1 (рабочий капитал предприятия в начале первого временного интервала – в натуральных единицах).

Практические расчеты экономической динамики производственной сферы предприятия с неоклассической производственной функцией проведем для случаев α < 1, α > 1 и различных комбинаций управляемых параметров γt и βt и для следующих рыночных и технологических констант:

τ = 0,20; р = 2; с(1) = 1,2;

ρ = 0,15; v1 = 16; CPK1 = 0.

Характер динамики конечного продукта (нераспределенной прибыли) для различных комбинаций экзогенных и эндогенных параметров отражен в таблице 2.

Расчеты экономической динамики производственной сферы предприятия с неоклассической производственной функцией, основанные на соотношениях (1)-(12), позволили сделать следующие выводы, часть из которых согласуются с выводами работ [1,3,5], полученными для частного случая линейной производственной функции:

1. Масштаб производства (степень однородности производственной функции), являясь фактором модели «выпуск-затраты», существенно влияет на экономическую динамику предприятия, что прямо следует из результатов, приведенных в таблице 2 для случаев растущей и снижающейся отдачи от масштаба производства.

2. Выбор управляемых параметров модели «выпуск-затраты» (γt – доля инвестиций из собственных средств в активы рабочего капитала, kt – доля собственных средств в пассивах рабочего капитала) является корректным.

3. Пороговым значением показателя γt является 0,4, что подтверждается сравнительным анализом динамики выпуска для значений показателя соответственно меньших и больших приведенного значения.

Таблица 2

Варианты расчетов экономической динамики производственной сферы предприятия с неоклассической производственной функцией с критерием (11)

4. Аналогично случаю линейной производственной функции важную роль для улучшения динамики выпуска играет фактор налогового щита: с ростом финансового рычага (доли заемных средств в производственном капитале) выпуск и рентабельность затрат растут.

В целом, приведенные теоретические обоснования модели динамики «выпуск-затраты» и практические расчеты по модели с критерием на максимум выпуска в конце планового периода убедительно демонстрируют актуальность постановки задачи оптимизации экономической динамики производственного сегмента предприятия в условиях выделения в его структуре центров прибыли и инвестиций.