Введение
В настоящее время перед российской экономикой стоит задача перехода на качественно новый уровень развития, обеспечивающий ей устойчивое развитие и лидерство на мировых рынках. На этом уровне развития производительных сил, основанном на инновационности производства, внедрением наукоёмких технологий во многом, к числу наиболее важных факторов развития относится нематериальная сфера экономики, основанная на знаниях. Знания становятся стратегическим ориентиром формирования российской политики. Применение фундаментальных знаний и их применение при создании наукоёмких производств приобретает огромное значение, возведённое в ранг национальных программ. В связи с этим для формирования российской экономики будущего решающее значение имеет развитие института магистратуры, к выпускникам которой предъявляются повышенные требования в системе высшего образования. Сегодня магистратура – это второй уровень иерархии в системе высшего образований после бакалавриата. Отправной точной перехода российских вузов на подготовку по магистерским программам является Приказ Министерства образования и науки от 22 марта 2006 года № 62 «Об образовательной программе высшего профессионального образования специализированной подготовки магистров» [1]. Приказ целеориентирован на «формирование высококвалифицированных специалистов, подготовленных к различным видам инновационной деятельности, требующей фундаментальной и специальной подготовки» [1]. Переход высшей школы на выполнение магистерских программ обусловил необходимость управления процессом формирования высококвалифицированных кадров по определённым видам программ, обеспечивая непрерывность образования, а также формирования контингента магистрантов, как главного фактора конкурентного преимущества любого образовательного учреждения. В этой связи в процессы принятия решений в сфере формирования контингента магистрантов стали испытывать необходимость в применении экономико-математического инструментария, а также построенного на его основе комплекса программных средств, включённого в контур управления. Решаемые авторами теоретические и практические проблемы, возникшие в процессе построения экономико-математического инструментария, основываются на подходах и математическом аппарате, разработанном в исследованиях отечественных учёных. Так, в работе [2] изложены общие теоретико-методологические подходы в аспекте применения методологии системного подхода и системного анализа к решению задач менеджмента в условиях риска. Вопросы применения методологии системного анализа при математическом моделировании стратегического управления экономическими системами освещены в работах [3, 4, 5]. Созданию адаптивных экономико-математических моделей на основе применения математического аппарата теории стохастических автоматов, способных к обучению в условиях вариаций воздействий окружающей среды, посвящены работы [6, 7, 8]. Вопросам анализа экономических систем в условиях антикризисного взаимодействия уделено внимание в статьях [9, 10]. Задачи описания различного рода конфликтных ситуаций в процессе создания модельного инструментария решены в работах [11, 12, 13].
Однако, проблематика разработки теоретико-методологических подходов в управлении формированием контингента магистрантов разработана в настоящее время недостаточно. Разработанные в научной литературе подходы, методы и инструменты неприменимы для решения задач управления движением контингента обучающихся при выполнении магистерской программы. Управление формированием контингента магистрантов высшего учебного заведения рассматривается авторами как системно целеориентированный процесс функционирования вузовских структур. Этот процесс выполняется под действием различных информационно-распорядительных документов, содержащих управляющие решения. Решения, обычно, принимаются в условиях неопределённости воздействий внешней среды и способствуют достижению целей высшей школы. Процесс принятия решений при управлении формированием контингента магистрантов испытывает значительную необходимость в применении экономико-математического инструментария для оценки последствий управления.
Постановка задачи
Поддержка принятия решений трактуется авторами как помощь лицу, принимающему решение в процессе выбора управленческих решений в условиях неопределённости влияния внешней и внутренней среды. В виду того, что условия неопределённости постоянно сопутствуют в процессе управления образовательным учреждением, процессы прогнозирования являются неотъемлемой частью системы поддержки принятия решений. В современной научной литературе известен широкий спектр работ, в которых рассматривались теоретико-методологические вопросы управления в условиях неопределённости [5, 6]. Условия стохастической неопределённости рассматривались в [12, 13]. Следовательно, анализ публикаций, касающихся проблематики построения модельного инструментария поддержки принятия решений в условиях неопределённости, подтверждают наличие теоретико-методологической базы для исследований в области формирования контингента магистрантов высших учебных заведений. О значимость поставленной задачи свидетельствует тот факт, что экстраполируемые характеристики движения контингента магистрантов используются в качестве исходных данных при планировании потребности высшего учебного заведения в трудовых и материальных ресурсах. Прогнозируемые показатели движения контингента являются базой для определения состава должностей профессорско-преподавательского состава для выполнения магистерской программы. Поэтому в условиях роста конкуренции между отечественными и зарубежными образовательными учреждениями использование в процессе анализа и управления экономико-математического инструментария прогнозирования степени сохранности и потери контингента магистрантов играет стратегическую роль. Н основе применения системного подхода в статье предлагается представить процесс прогнозирования показателей движения контингента предложено, как последовательность взаимодействующих между собой динамических систем I = <I1, I2, I3, I4>. При этом каждая система Ii,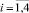 
, рассматриваемая как математическая абстракция, выполняет следующие функции:
а) имитирует динамику движения контингента магистрантов с помощью генерирования значений случайных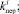 
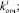
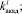
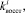которые соответственно описывают магистрвнтов, переведённых на курс обучения с номером i, 
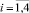из других учреждений высшего образования; количество магистрантов, являющихся отчисленными с курса номер i; количество магистрантов, покинувших обучение в течение курса номер i по причине академического отпуска; количество магистрантов, возвратившихся на обучение после отчисления на курс номер i;
б) имитирует динамику количества Wi магистратнов при переходе на курсы с номером i + 1;
в) составляет прогнозы степени потери и сохранности контингента магистрантов посредством вычисления величин оценок вероятностей потерь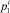 
и сохранности 
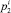контингента:
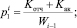
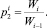
Динамическая система Ii,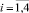 
реализует отображения:
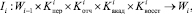
где Wi – показатель состояния системы, характеризующего число магистрантов, которые успешно закончили курс обучения с номером i и число магистрантов, которые переведены на следующий курс с номером i + 1. Система взаимодействует с внешней средой Взаимодействие системы с внешней средой осуществляется с помощью возмущений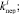 
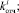
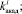
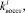
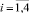, которые оказывают влияние на изменение состояния Wi в соответствии с выражением:
.
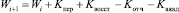За период отрезков времени (семестр, учебный год и др.) на систему Ii воздействует входной сигнал Wi–1, который наряду с возмущениями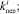 
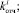
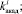
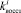осуществляет переход её в новое состояние Wi. От этого состояния зависят величины выходных сигналов 
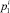и 
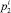. Динамическая система Ii, 
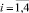реализована в виде имитационной модели, которая в процессе функционирования позволяет оценить реакцию состояния Wi на изменения возмущений.
Имитационное моделирование трактуется как тип математического моделирования, при котором построенная имитационная модель объекта воспроизводит алгоритм его функционирования. При этом воспроизводятся все случайные явления в процессе движении контингента магистрантов при сохранении их логической структуры. В процессе имитационного моделирования авторами статьи выполнено формальное описание на алгоритмическом языке логики функционирования исследуемого объекта. Разработанный алгоритм затем отображается в памяти компьютера с целью проведения статистических экспериментов.
Процесс построения имитационной модели реализовывался по следующим этапам:
– идентификация входных, выходных параметров модели, а также величин состояний и возмущений;
– построение концептуальной модели формирования контингента магистрантов в виде некоторой абстракции по аналогии динамической системы;
– определение функций перехода
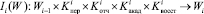
имитационной модели в новое состояние и функции выхода
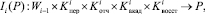
где P = (p1, p2);
– задание процедуры исследования вероятностных законов распределения возмущений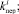 
;
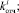
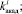
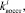
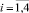– задание алгоритма генерирования возможных значений возмущений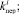 
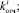
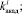
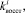
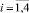по заданным вероятностным законам;
– построение процедуры определения значений состояний Wi в виде алгоритма посредством реализации функции перехода
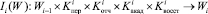
и значений выходных показателе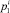й 
и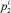 
, а также посредством реализации функции выхода
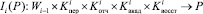
в условиях стохастической неопределённости, формируемой случайно изменяющимися возмущениями;
– описание построенного алгоритма с помощью языка высокого уровня Delphi;
– проведение имитационных экспериментов при реализации процессов движения контингента для конкретного образовательного учреждения.
Следовательно, предложенная имитационная модель позволяет воспроизводить динамику контингента магистрантов вуза и количественно оценивать с помощью прогноза степень сохранности и потери контингента в течение планируемого промежутка времени. Концептуальная схема имитационной модели представлена на рис. 1.
Концептуальная схема, приведённая на рис. 1, описывает с кибернетических позиций модель формирования контингента магистрантов на учебном курсе с номером i. Входным воздействием имитационной модели является детерминированная величина количества магистрантов Wi–1, которые поступили на курс i в начале периода исследования.
Рис. 1. Концептуальная схема имитационной модели движения контингента
Методы исследования
Число магистрантов Wi, которые успешно окончили курс с номером i и переведены на курс с номером i + 1, изменяется при поступлении случайно изменяющихся величин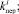 
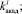
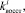
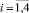. Величиной Wi+1 описываются значения выходных сигналов P = (p1, p2) имитационной модели.
Изменяющиеся случайным образом величины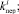 
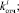
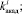
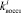требуют их воспроизведения с помощью метода статистических испытаний. С этой целью в имитационной модели предусмотрен блок формирования исходных данных. Его функция – построение закона распределения вероятностей случайных величин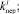 
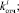
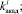
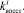Для проведения исследований были собраны статистические данные, характеризующие каждую из этих величин. Статистические данные представлены следующими выборками из генеральных совокупностей:
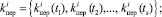
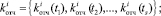
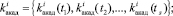
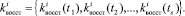
Эта статистика использовалась при построении законов распределения вероятностей F1, F2, F3, F4:
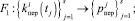
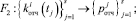
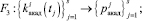
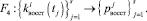
Вследствие дискретного характера случайных величин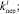 
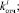
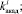
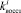и конечности множества их возможных значений законы распределения вероятностей F1, F2, F3, F4 построены в виде интервальных рядов распределения. Алгоритм построения интервального ряда распределения исходя из статистических данных Y = {y1, y2, ..., ys} представлен последовательностью следующих шагов.
Шаг 1. Интервал изменений [ymin; ymax] выборочных данных случайной величины Y = {y1, y2, ..., ys} разбивается на частичные интервалы длиной Δ и определяемой выражениями:
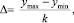
где k – количество частичных интервалов.
Шаг 2. Определяются координаты концов для каждого частичного интервала. За начало первого интервала принимается величина ymin. Координата конца первого интервала определяется в виде суммы (ymin + Δ) и рассматривается одновременно, как начало следующего интервала, и т. д.
Шаг 3. Вычисляются относительные частоты mi попадания значений {y1, y2, ..., ys} случайной величины Y в каждый частичный интервал Δi с номером i.
Блок 4. Определяются относительные частоты попадания значений {y1, y2, ..., ys} в интервал с номером i как отношение mi /s.
Шаг 5. Составляется таблица, первая строка которой содержит частичные интервалы Δi, а вторая – относительные частоты mi /s попадания в эти интервалы значений случайной величины Y. Построенная таблица представляет собой интервальный ряд распределения как один из видов законов распределения вероятностей.
Построенный алгоритм воплощён в компьютерной программе на алгоритмическом языке Delphi. Реализованная по алгоритму программа строит законы распределения вероятностей F1, F2, F3, F4 случайных величин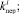 
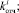
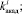
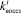на основе собранных статистических данных.
Законы распределения вероятностей F1, F2, F3, F4 служат исходными данными при генерации возможных значений случайных величин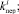 
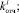
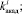
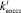по методу статистических испытаний. На базе применения этого метода авторами построен алгоритм для разыгрывания возможных значений случайных величин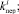 
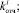
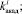
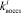по заданным законам распределения вероятностей. Этот алгоритм представляет собой следующую последовательность шагов.
Шаг 1. Отрезок [0, 1] разбивается на подинтервалы ωi длиной mi /s. Блок 2. Разыгрывается число x по равномерному закону распределения. Получение последовательности равномерно распределённых случайных чисел не является сложной задачей, т. к. реализуется в любом языке программирования по команде RANDOMISE.
Шаг 3. Идентифицируется интервал ωα, в который попала величина x.
Шаг 4. Середина интервала ωα рассматривается как возможное значение случайной величины, распределённой по заданному закону.
Сгенерированные возможные значения случайных величин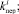 
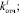
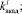
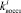используются в имитационной модели для определения величин
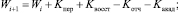
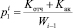и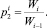 
Построенная имитационная модель является стержнем программного продукта MAGISTRANT. Интерфейс программы приведён на рис. 2.
Рис. 2. Интерфейс имитационной модели движения контингента студентов образовательного учреждения
Программный продукт MAGISTRANT даёт возможность на основе введённых в компьютер ретроспективных статистических данных оценивать состояние учебного процесса магистратуры в перспективе. Как инструментарий системы поддержки процесса принятия решений, созданный программный продукт позволяет оценивать в будущем значения таких важных показателей, как вероятность потери и сохранности контингента магистрантов.
Выводы
1. Предложена и формальная постановка задачи прогнозирования движения контингента магистрантов в виде последовательности взаимодействующих динамических систем.
2. Построена имитационная модель прогнозирования потерь и сохранности контингента магистрантов в условиях стохастической неопределённости.
3. Произведена программная реализация построенной имитационной модели на языке высокого уровня Delphi.