Введение
Повышение эффективности рыночной деятельности производственной корпорации является основной стратегией сохранения высоких финансово-экономических показателей, обеспечивающих конкурентоспособное развитие, финансовую устойчивость и перспективы роста в условиях турбулентной рыночной среды. На кратко- и среднесрочном интервалах планирования для достижения цели устойчивого, конкурентоспособного развития менеджмент и собственники ориентируются на критерий максимизации чистой прибыли, являющейся источником пополнения резервов и рабочего капитала производственной сферы корпорации. В связи с этим особую актуальность приобретает проблематика оценки качества и корректного принятия решений при управлении денежными потоками производственной сферы корпорации с учетом рыночного спроса на продукцию, возможных объемов и стоимости собственного и заемного капитала, направляемого в финансирование затрат и инвестирование перспективных проектов в этой сфере. Возможным и вполне эффективным инструментом решения этой проблемы является разработка и адаптация инструментария экономико-математических моделей и методов оптимального управления производственной сферой предприятия в статичном и динамическом вариантах. Второй представляется более актуальным, так как позволяет выбрать комбинацию управляемых параметров на основе наблюдаемого на последовательности временных интервалов тренда денежного потока, включающего потоки инвестиций в рабочий капитал, потоки кредитов, потоки платежей с агентами рынка, финансовыми и кредитными организациями и государством.
Цель исследования – разработка и верификация динамической модели управления денежными потоками производственной сферы предприятия с неоклассической функцией «затраты-выпуск»; проверка устойчивости экономической динамики производственной сферы такого предприятия при изменениях эндогенных (управляемых) параметров, характеризующих доли заемного финансирования производственных затрат (риск структуры рабочего капитала) и отчислений из прибыли на собственные инвестиции в рабочий капитал.
Методологическая основа исследования
Настоящая работа является прямым продолжением исследований проф. М.А. Халикова и его учеников, опубликованных в статьях [2,9,10]. Вид и свойства неоклассической зависимости в паре «выпуск-затраты» авторы заимствовали из работ Г.Б. Клейнера [4,5,6], Ф. Турино, П. Самуэльсона и Р. Солоу [14,15,16]. Необходимо также подчеркнуть определенную связь изложенного материала с работами М.А. Бендикова [2], Б. Коласса [7], М. Круи [8] и Ю.Е. Хрусталева [11], посвященными повышению эффективности и устойчивости высокотехнологичных предприятий и холдингов. Математический аппарат для расчетов по динамической модели авторы разработали самостоятельно, а также частично заимствовали из работ Н.П. Бахвалова [1,12,13], Р. Дорфмана [12] и Д. Лиенберга [13].
Результаты исследования и их обсуждение
1. Основные понятия и соотношения динамической модели «затраты-выпуск»
В соответствии с функциями и особенностями управления рабочим (или производственным) капиталом производственной сферы предприятия на этапах его формирования, использования и воспроизводства приведем следующую принципиальную схему денежных потоков его производственной сферы (рис. 1).
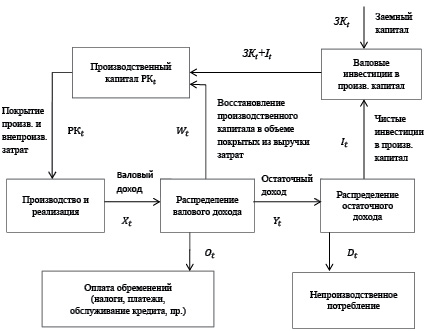
Рис. 1. Схема денежных потоков производственной сферы предприятия
Баланс денежных и материальных потоков описывается следующими соотношениями:
Xt = Wt + Ot + Yt ; (1)
Xt ≤ min{F(t;PKt);Spt}; (2)
Ot = τ (Xt – Wt – ρt · ЗKt-1) + (1 + ρt) · ЗKt-1 =
= τ (Xt – Wt) + (1 + ρt(1–τ)) · ЗKt-1; (3)
Yt = It + Dt ; (4)
PKt+1 = Wt + It + ЗKt+1 ; (5)
Wt, It, Dt ≥ 0, (6)
PK0 = PKн, (7)
где t – индекс интервала планирования (t = 0,T); F(t;PKt) – производственная функция, устанавливающая зависимость в паре «валовый доход производственной деятельности – затраты производственного капитала» в условиях реализации выбранного на шаге t варианта производственной деятельности (производственной программы); Spt – рыночный спрос (в стоимостном выражении) для шага t; τ – налог на прибыль хозяйствующего субъекта; ρt – ставка по кредитам для периода t ; PKн – величина производственного капитала в конце нулевого интервала планирования, равная сумме первоначального объема текущих активов и первоначальным собственным инвестициям в капитал производственной сферы.
Из (1), (3) и (4) следует:
Xt = τXt + (1–τ) Wt + (1 + ρt(1–τ)) · ЗKt-1 + Dt + It,
откуда:
(1–τ) Xt = (1–τ) Wt + (1 + ρt(1–τ)) · ЗKt-1 + Dt + It,
или
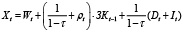 . (8)
. (8)
На основании (8) можно привести выражение для остаточного дохода (суммы чистых инвестиций и непроизводственного потребления):
Dt + It = (1–τ) (Xt – Wt) – (1 + ρt(1–τ)) · ЗKt-1. (9)
Отметим, что соотношения (1)-(9), описывающие трансформацию производственного капитала предприятия на этапах производственно-коммерческого цикла, не включают элементы, связанные с амортизацией основного капитала. В данном случае это сделано сознательно с целью упрощения модели. Однако, здесь и далее будем считать, что амортизация используется исключительно для восстановления (реновации) основного капитала в данном или следующих плановых периодах и не используется в финансировании затрат текущей производственной деятельности (включая и оплату труда).
С учетом сделанных замечаний можно утверждать, что система уравнений (1)-(9) корректно задает Т-шаговую процедуру трансформации производственного капитала по величине и структуре и может служить основой динамической модели выбора их оптимальных по выбранному критерию величин. В качестве таких критериев рассматриваются:
- дисконтированный поток доходов собственников:
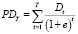 , (10)
, (10)
где e – ставка дисконтирования доходов (как правило, планируемая ставка доходности собственного капитала);
- средняя за период отдача (рентабельность) производственного капитала, авансированного в затраты:
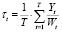 , (11)
, (11)
- средний за период индекс доходности собственных инвестиций в производственный капитал:
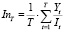 . (12)
. (12)
При этом в составе системы ограничений динамической модели предлагается дополнительно учитывать: максимально допустимый риск структуры капитала (доля заемных средств в производственном капитале) – для моделей с критериями (11), (12); минимально допустимую рентабельность и максимально допустимый риск структуры производственного капитала – для модели с критерием (10).
2. Постановка задачи моделирования экономической динамики предприятия с неоклассической производственной функцией
Рассмотрим постановку задачи моделирования экономической динамики предприятия для важного частного случая, когда зависимость между выпуском и затратами задается неоклассической производственной функцией степени однородности α (α > 0). Напомним, что если в границах экономической области предприятия производственная функция является однородной степени α, то зависимость в паре «выпуск-затраты» задается соотношением:
c(vt) = c(1) · vt1/α, (13)
где vt – величина выпуска (в натуральном или стоимостном выражениях) для периода планирования t; c(vt) – совокупные затраты на объем выпуска vt; c(1) – удельные затраты.
Из (13) следует:
vt = (c(vt) / c(1))α. (13’)
Выше введено понятие производственного капитала, включающего текущие активы, формируемые на основе собственных и заемных средств и авансируемые в покрытие производственных и внепроизводственных затрат (постоянных и переменных) операционной деятельности.
Так как производственный капитал полностью покрывает затраты, то представим (13’) в виде:
vt = (PKt)α / z, (14)
где PKt – производственный капитал, сформированный в начале периода t и направляемый на покрытие затрат операционной деятельности этого периода; z = (c(1))α.
Если βt – доля заемного капитала, а CsPKt – величина собственных средств в производственном капитале для периода t, то
PKt = CsPKt / (1 – βt). (15)
CsPKt – часть собственного капитала Cst предприятия в начале периода t, который образуется из чистой прибыли и покрытых из выручки затрат операционной деятельности периода (t – 1)
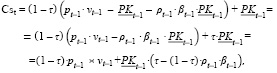 (16)
(16)
где τ – налог на прибыль; pt–1 – стоимость продукции для периода (t – 1); ρt–1 – стоимость заёмных средств (в объёме βt–1 · PKt–1), включаемых в производственный капитал для периода (t – 1).
Напомним, что производственный капитал PKt, формируемый для периода t, образуется путем выделения собственниками регулируемой доли γt из собственных средств Cst на начало периода t и краткосрочного кредита, доля которого соответствует рычагу капитала βt:
PKt = γt · Cst / (1 – βt) (17)
или с учетом (16):
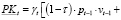
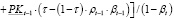 (18)
(18)
На основании (14) делаем вывод, что:
PKt = (vt-1 · z)1/α или
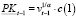 (14’’)
(14’’)
С учетом (14’’) представим (18) в виде:
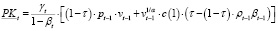 (19)
(19)
Используя соотношения (14) и (19), получим следующее рекуррентное уравнение, связывающее выпуски vt и vt-1 на последовательных интервалах планирования:
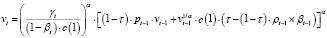 (20)
(20)
Возвращаясь к формуле (16) расчета величины Cst собственного капитала по завершении периода (t – 1), определим ту его часть, которая направляется в фонд потребления и в дальнейшем выплачивается акционерам в форме дивидендов.
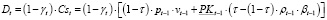 (21)
(21)
где Dt – абсолютный прирост фонда потребления в конце периода t.
В динамической модели предприятия, задаваемой соотношениями (19) – (21), экзогенными (неуправляемыми) параметрами являются: ставка τ налогообложения прибыли, вектора p и ρ цен соответственно товарного и финансового рынков (по интервалам планирования).
Детерминантами модели являются показатели используемой технологии: α – степень однородности (суммарная эластичность производственной функции), c(1) – удельные затраты.
Эндогенными (управляемыми) параметрами являются: v1 – объем выпуска в первом плановом периоде, вектора 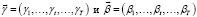 относительных долей соответственно пополнения производственного капитала предприятия из собственных средств и финансирования операционной деятельности из заёмных источников.
относительных долей соответственно пополнения производственного капитала предприятия из собственных средств и финансирования операционной деятельности из заёмных источников.
Таким образом, уравнения (19) – (21) задают возможные траектории изменения объемов средств в производственном капитале и в фонде потребления предприятия в зависимости от проводимой собственниками и менеджментом политики в сфере финансирования производственной деятельности. Последняя включает выбор структуры производственного капитала (управление долей βt заёмных средств) и его объёма (управление долей γt собственных средств, вкладываемых в производство).
3. Эмпирические расчеты по динамической модели
Практическое значение динамической модели, построенной на основе уравнений (19), (20) и (21), заключается в возможности решения следующих задач производственного и финансового планирования:
- выбор оптимального по рыночному критерию (максимум финансового результата операционной деятельности) объёма производства, величины и структуры производственного капитала для следующего интервала планирования, исходя из его величины и структуры в текущем периоде, изменений экзогенных и эндогенных параметров функционирования предприятия;
- определение оптимальных пропорций в собственные инвестиции в рабочий капитал и непроизводственное потребление.
Для дальнейшего исследования экономической динамики предприятия с нелинейной неоклассической производственной функцией, задаваемой уравнениями (19) – (21), будем предполагать заданными: ставку τ налогообложения прибыли, цены p – товарного и ρ – финансового рынков, а также технологические константы: c(1) (удельные затраты) и v1 (выпуск на первом интервале планирования – в натуральных единицах).
В первой части эмпирических исследований экономической динамики предприятия с неоклассической производственной функцией представим результаты расчетов по динамической модели для случая функции степени однородности α = 0,79 по нашим исследованиям достаточно приближенный к реальной практике реального сектора экономики масштаб производства производственных корпораций) и для различных комбинаций управляемых параметров γt и βt. Эти расчеты проведены для следующих рыночных и технологических констант: τ = 0,20; p = 2; c(1) = 1,2; ρ= 0,15; v1 = 16; CS1 = 0. Характер динамики выпуска для различных комбинаций параметров α, γt, βt отражен в табл. 1-10, а результаты расчетов приведены на рисунках 2-11.
Таблица 1
(для значений параметров α = 0,79, β = 0,2, γ = 0,4)
|
t |
PKt |
vt |
Dt |
|
1 |
0,000 |
16,000 |
0,000 |
|
2 |
16,331 |
7,865 |
15,360 |
|
3 |
7,729 |
4,356 |
9,275 |
|
4 |
4,165 |
2,673 |
4,998 |
|
5 |
2,505 |
1,788 |
3,006 |
|
6 |
1,651 |
1,287 |
1,981 |
|
7 |
1,175 |
0,983 |
1,410 |
|
8 |
0,890 |
0,790 |
1,068 |
|
9 |
0,710 |
0,661 |
0,852 |
|
10 |
0,591 |
0,571 |
0,709 |
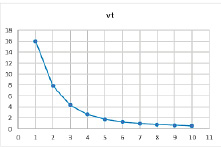
Рис. 2. Результат расчетов при значениях параметров α = 0,79, β = 0,2, γ = 0,4
Таблица 2
(для значений параметров α = 0,79,β = 0,4, γ = 0,4)
|
t |
PKt |
vt |
Dt |
|
1 |
0,000 |
16,000 |
0,000 |
|
2 |
21,132 |
9,642 |
15,360 |
|
3 |
12,426 |
6,338 |
11,183 |
|
4 |
8,020 |
4,485 |
7,218 |
|
5 |
5,596 |
3,375 |
5,037 |
|
6 |
4,167 |
2,674 |
3,751 |
|
7 |
3,274 |
2,210 |
2,947 |
|
8 |
2,689 |
1,892 |
2,420 |
|
9 |
2,290 |
1,666 |
2,061 |
|
10 |
2,009 |
1,503 |
1,809 |
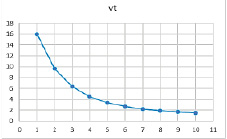
Рис. 3. Результат расчетов при значениях параметров α = 0,79, β = 0,4, γ = 0,4
Таблица 3
(для значений параметров α = 0,79, β = 0,6, γ = 0,4)
|
t |
PKt |
vt |
Dt |
|
1 |
0,000 |
16,000 |
0,000 |
|
2 |
30,736 |
12,962 |
15,360 |
|
3 |
24,674 |
10,897 |
14,804 |
|
4 |
20,594 |
9,447 |
12,356 |
|
5 |
17,751 |
8,401 |
10,651 |
|
6 |
15,714 |
7,630 |
9,428 |
|
7 |
14,219 |
7,050 |
8,531 |
|
8 |
13,101 |
6,609 |
7,860 |
|
9 |
12,251 |
6,267 |
7,350 |
|
10 |
11,596 |
6,001 |
6,958 |
Рис. 4. Результат расчетов при значениях параметров α = 0,79, β = 0,6, γ = 0,4
Таблица 4
(для значений параметров α = 0,79, β = 0,8, γ = 0,4)
|
t |
PKt |
vt |
Dt |
|
1 |
0,000 |
16,000 |
0,000 |
|
2 |
59,545 |
21,856 |
15,360 |
|
3 |
82,326 |
28,231 |
24,698 |
|
4 |
107,462 |
34,845 |
32,238 |
|
5 |
133,855 |
41,447 |
40,157 |
|
6 |
160,471 |
47,831 |
48,141 |
|
7 |
186,437 |
53,848 |
55,931 |
|
8 |
211,092 |
59,399 |
63,328 |
|
9 |
233,984 |
64,432 |
70,195 |
|
10 |
254,852 |
68,931 |
76,456 |
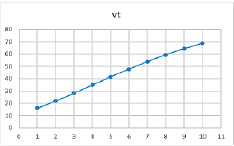
Рис. 5. Результат расчетов при значениях параметров α = 0,79, β = 0,8, γ = 0,4
Таблица 5
(для значений параметров α = 0,79, β = 0,9, γ = 0,4)
|
t |
PKt |
vt |
Dt |
|
1 |
0,000 |
16,000 |
0,000 |
|
2 |
117,165 |
37,308 |
15,360 |
|
3 |
281,885 |
74,646 |
42,283 |
|
4 |
581,465 |
132,258 |
87,220 |
|
5 |
1060,428 |
212,607 |
159,064 |
|
6 |
1750,920 |
315,956 |
262,638 |
|
7 |
2666,460 |
440,489 |
399,969 |
|
8 |
3800,389 |
582,789 |
570,058 |
|
9 |
5128,390 |
738,468 |
769,258 |
|
10 |
6613,444 |
902,786 |
992,017 |
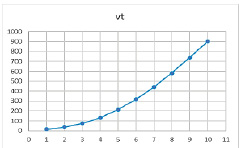
Рис. 6. Результат расчетов при значениях параметров α = 0,79, β = 0,9, γ = 0,4
Таблица 6
(для значений параметров α = 0,79, β = 0,2, γ = 0,8)
|
t |
PKt |
vt |
Dt |
|
1 |
0,000 |
16,000 |
0,000 |
|
2 |
32,661 |
13,600 |
5,120 |
|
3 |
27,508 |
11,875 |
5,502 |
|
4 |
23,841 |
10,606 |
4,768 |
|
5 |
21,165 |
9,653 |
4,233 |
|
6 |
19,171 |
8,927 |
3,834 |
|
7 |
17,658 |
8,366 |
3,532 |
|
8 |
16,494 |
7,927 |
3,299 |
|
9 |
15,587 |
7,581 |
3,117 |
|
10 |
14,873 |
7,305 |
2,975 |
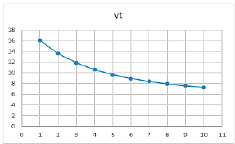
Рис.7. Результат расчетов при значениях параметров α = 0,79, β = 0,2, γ = 0,8
Таблица 7
(для значений параметров α = 0,79, β = 0,4, γ = 0,8)
|
t |
PKt |
vt |
Dt |
|
1 |
0,000 |
16,000 |
0,000 |
|
2 |
42,265 |
16,671 |
5,120 |
|
3 |
44,131 |
17,250 |
6,620 |
|
4 |
45,744 |
17,747 |
6,862 |
|
5 |
47,130 |
18,170 |
7,070 |
|
6 |
48,314 |
18,530 |
7,247 |
|
7 |
49,321 |
18,834 |
7,398 |
|
8 |
50,175 |
19,091 |
7,526 |
|
9 |
50,897 |
19,308 |
7,635 |
|
10 |
51,505 |
19,490 |
7,726 |
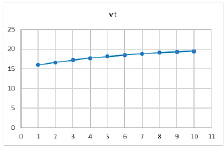
Рис. 8. Результат расчетов при значениях параметров α = 0,79, β = 0,4, γ = 0,8
Таблица 8
(для значений параметров α = 0,79, β = 0,6, γ = 0,8)
|
t |
PKt |
vt |
Dt |
|
1 |
0,000 |
16,000 |
0,000 |
|
2 |
61,471 |
22,413 |
5,120 |
|
3 |
87,458 |
29,612 |
8,746 |
|
4 |
117,148 |
37,303 |
11,715 |
|
5 |
149,360 |
45,195 |
14,936 |
|
6 |
182,861 |
53,030 |
18,286 |
|
7 |
216,509 |
60,600 |
21,651 |
|
8 |
249,346 |
67,752 |
24,935 |
|
9 |
280,638 |
74,385 |
28,064 |
|
10 |
309,874 |
80,442 |
30,987 |
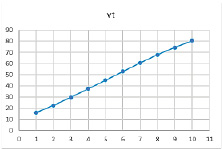
Рис. 9. Результат расчетов при значениях параметров α = 0,79, β = 0,6, γ = 0,8
Таблица 9
(для значений параметров α = 0,79, β = 0,8, γ = 0,8)
|
t |
PKt |
vt |
Dt |
|
1 |
0,000 |
16,000 |
0,000 |
|
2 |
119,091 |
37,791 |
5,120 |
|
3 |
291,405 |
76,630 |
14,570 |
|
4 |
611,658 |
137,654 |
30,583 |
|
5 |
1135,435 |
224,401 |
56,772 |
|
6 |
1908,508 |
338,217 |
95,425 |
|
7 |
2958,526 |
478,185 |
147,926 |
|
8 |
4291,134 |
641,474 |
214,557 |
|
9 |
5890,542 |
823,890 |
294,527 |
|
10 |
7723,365 |
1020,502 |
386,168 |
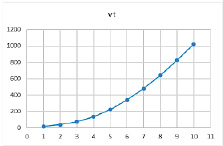
Рис. 10. Результат расчетов при значениях параметров α = 0,79, β = 0,8, γ = 0,8
Таблица 10
(для значенией параметров α = 0,79, β = 0,9, γ = 0,8)
|
t |
PKt |
vt |
Dt |
|
1 |
0,000 |
16,000 |
0,000 |
|
2 |
234,330 |
64,508 |
5,120 |
|
3 |
998,164 |
202,682 |
24,954 |
|
4 |
3328,984 |
524,896 |
83,225 |
|
5 |
9168,798 |
1168,621 |
229,220 |
|
6 |
21706,582 |
2308,629 |
542,665 |
|
7 |
45526,490 |
4144,532 |
1138,162 |
|
8 |
86557,507 |
6885,216 |
2163,938 |
|
9 |
151837,088 |
10733,351 |
3795,927 |
|
10 |
249138,989 |
15872,150 |
6228,475 |
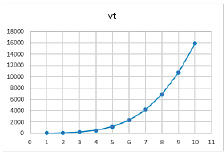
Рис. 11. Результат расчетов при значениях параметров α = 0,79, β = 0,9, γ = 0,8
Подробные расчеты экономической динамики предприятий с неоклассической производственной функцией для случаев 0,7 < α < 0,9 и различных значений экзогенных параметров γt, и βt отражены в таблице 11.
Расчеты экономической динамики предприятия с неоклассической производственной функцией, основанные на соотношениях (19)–(21) и отраженные в таблицах 1–11 и рисунках 1–11, позволяют сделать следующие выводы:
- масштаб производства (степень однородности производственной функции), являясь фактором модели «выпуск-затраты», существенно влияет на экономическую динамику производственной сферы предприятия, чувствительно отражаясь на доле заемного финансирования, с которой начинает активно работать «рычаг капитала», а именно, динамика производственной сферы переходит от умеренного падения к экспоненциальному росту;
- выбор управляемых параметров динамической модели (γt – темп накопления собственных средств в производственном капитале и βt – доля заемных средств в производственном капитале) является обоснованным: и тот и другой активно влияют на динамику как в связке, так и по-отдельности:
- пороговым значением показателя γt является 0,4, что подтверждается сравнительным анализом динамики выпуска для значений показателя соответственно меньших и больших этой величины;
- аналогично случаю линейной производственной функции важную роль для улучшения динамики выпуска играет фактор налогового щита: с ростом рычага капитала выпуск и рентабельность собственного капитала, размещаемого в производственном сегменте предприятия, растут.
Таблица 11
Расчеты экономической динамики предприятия с неоклассической производственной функцией
|
α |
γt |
βt |
Динамика «выпуск-затраты» |
|
0,83 |
0,1 |
0,3 |
Экспоненциальное падение |
|
0,83 |
0,2 |
0,7 |
Умеренное экспоненциальное падение |
|
0,83 |
0,8 |
0,3 |
Квазилинейный рост |
|
0,83 |
0,4 |
0,1 |
Экспоненциальное падение |
|
0,83 |
0,4 |
0,5 |
Умеренное экспоненциальное падение |
|
0,83 |
0,6 |
0,7 |
Квазилинейный рост |
|
0,83 |
0,8 |
0,5 |
Линейный рост |
|
0,75 |
0,1 |
0,1 |
Экспоненциальное падение |
|
0,75 |
0,1 |
0,7 |
Умеренное экспоненциальное падение |
|
0,75 |
0,7 |
0,5 |
Квазилинейное падение |
|
0,75 |
0,8 |
0,5 |
Квазилинейный рост |
|
0,75 |
0,5 |
0,7 |
Умеренное экспоненциальное падение |
|
0,86 |
0,1 |
0,1 |
Экспоненциальное падение |
|
0,86 |
0,1 |
0,4 |
Умеренное экспоненциальное падение |
|
0,86 |
0,8 |
0,3 |
Квазилинейный рост |
|
0,86 |
0,4 |
0,1 |
Квазилинейное падение |
|
0,86 |
0,7 |
0,5 |
Экспоненциальный рост |
|
0,86 |
0,1 |
0,3 |
Квазилинейный рост |
|
0,8 |
0,1 |
0,5 |
Заметный экспоненциальный рост |
|
0,8 |
0,4 |
0,5 |
Умеренное экспоненциальное падение |
|
0,8 |
0,8 |
0,5 |
Экспоненциальный рост |
|
0,8 |
0,6 |
0,4 |
Экспоненциальное падение |
Во второй части эмпирических исследований экономической динамики предприятия с неоклассической производственной функцией (степени однородности α = 0,79) представим результаты расчетов по динамической модели (таблицы и рисунки 12-21) для варианта, когда ставка по кредиту монотонно возрастает с ростом рычага капитала, в данном случае характеризующего риск структуры рабочего капитала. Будем предполагать, что стоимость кредита зависит от структуры капитала следующим образом:
ρt = ρ0(1 + βt2).
Таблица 12
(для значений параметров α = 0,79, β = 0,2, γ = 0,4)
|
t |
PKt |
vt |
Dt |
|
1 |
0,000 |
16,000 |
0,000 |
|
2 |
16,311 |
7,858 |
15,360 |
|
3 |
7,714 |
4,349 |
9,257 |
|
4 |
4,154 |
2,667 |
4,985 |
|
5 |
2,497 |
1,784 |
2,997 |
|
6 |
1,646 |
1,284 |
1,975 |
|
7 |
1,171 |
0,981 |
1,405 |
|
8 |
0,887 |
0,788 |
1,065 |
|
9 |
0,708 |
0,659 |
0,849 |
|
10 |
0,589 |
0,570 |
0,707 |
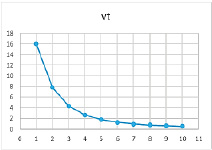
Рис. 12. Результат расчетов при значениях параметров α = 0,79, β = 0,2, γ = 0,4
Таблица 13
(для значений параметров α = 0,79, β = 0,4, γ = 0,4)
|
t |
PKt |
vt |
Dt |
|
1 |
0,000 |
16,000 |
0,000 |
|
2 |
20,927 |
9,568 |
15,360 |
|
3 |
12,219 |
6,255 |
10,997 |
|
4 |
7,847 |
4,408 |
7,063 |
|
5 |
5,457 |
3,309 |
4,912 |
|
6 |
4,054 |
2,616 |
3,649 |
|
7 |
3,181 |
2,160 |
2,863 |
|
8 |
2,610 |
1,848 |
2,349 |
|
9 |
2,222 |
1,627 |
2,000 |
|
10 |
1,949 |
1,467 |
1,754 |
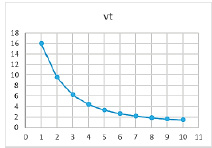
Рис. 13. Результат расчетов при значениях параметров α = 0,79, β = 0,4, γ = 0,4
Таблица 14
(для значений параметров α = 0,79, β = 0,6, γ = 0,4)
|
t |
PKt |
vt |
Dt |
|
1 |
0,000 |
16,000 |
0,000 |
|
2 |
29,696 |
12,615 |
15,360 |
|
3 |
23,215 |
10,385 |
13,929 |
|
4 |
18,986 |
8,859 |
11,391 |
|
5 |
16,113 |
7,782 |
9,668 |
|
6 |
14,097 |
7,002 |
8,458 |
|
7 |
12,643 |
6,425 |
7,586 |
|
8 |
11,571 |
5,991 |
6,943 |
|
9 |
10,767 |
5,660 |
6,460 |
|
10 |
10,155 |
5,404 |
6,093 |
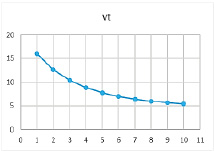
Рис. 14. Результат расчетов при значениях параметров α = 0,79, β = 0,6, γ = 0,4
Таблица 15
(для значений параметров α = 0,79, β = 0,8, γ = 0,4)
|
t |
PKt |
vt |
Dt |
|
1 |
0,000 |
16,000 |
0,000 |
|
2 |
54,615 |
20,414 |
15,360 |
|
3 |
69,973 |
24,828 |
20,992 |
|
4 |
85,406 |
29,062 |
25,622 |
|
5 |
100,267 |
32,989 |
30,080 |
|
6 |
114,098 |
36,534 |
34,229 |
|
7 |
126,621 |
39,667 |
37,986 |
|
8 |
137,711 |
42,387 |
41,313 |
|
9 |
147,360 |
44,716 |
44,208 |
|
10 |
155,636 |
46,689 |
46,691 |
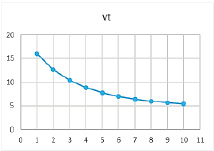
Рис. 15. Результат расчетов при значениях параметров α = 0,79, β = 0,8, γ = 0,4
Таблица 16
(для значений параметров α = 0,79, β = 0,9, γ = 0,4)
|
t |
PKt |
vt |
Dt |
|
1 |
0,000 |
16,000 |
0,000 |
|
2 |
103,125 |
33,729 |
15,360 |
|
3 |
217,731 |
60,870 |
32,660 |
|
4 |
393,505 |
97,153 |
59,026 |
|
5 |
628,896 |
140,710 |
94,334 |
|
6 |
911,913 |
188,717 |
136,787 |
|
7 |
1224,273 |
238,161 |
183,641 |
|
8 |
1546,365 |
286,420 |
231,955 |
|
9 |
1861,046 |
331,555 |
279,157 |
|
10 |
2155,597 |
372,362 |
323,340 |
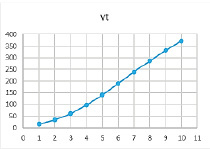
Рис. 16. Результат расчетов при значениях параметров α = 0,79, β = 0,9, γ = 0,4
Таблица 17
(для значений параметров α = 0,79, β = 0,2, γ = 0,8)
|
t |
PKt |
vt |
Dt |
|
1 |
0,000 |
16,000 |
0,000 |
|
2 |
32,623 |
13,587 |
5,120 |
|
3 |
27,450 |
11,855 |
5,490 |
|
4 |
23,772 |
10,581 |
4,754 |
|
5 |
21,091 |
9,627 |
4,218 |
|
6 |
19,095 |
8,900 |
3,819 |
|
7 |
17,582 |
8,338 |
3,516 |
|
8 |
16,418 |
7,899 |
3,284 |
|
9 |
15,511 |
7,552 |
3,102 |
|
10 |
14,798 |
7,276 |
2,960 |
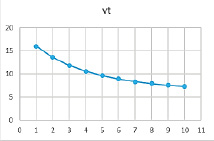
Рис. 17. Результат расчетов при значениях параметров α = 0,79, β = 0,2, γ = 0,8
Таблица 18
(для значений параметров α = 0,79, β = 0,4, γ = 0,8)
|
t |
PKt |
vt |
Dt |
|
1 |
0,000 |
16,000 |
0,000 |
|
2 |
41,854 |
16,543 |
5,120 |
|
3 |
43,346 |
17,007 |
6,502 |
|
4 |
44,623 |
17,402 |
6,693 |
|
5 |
45,711 |
17,736 |
6,857 |
|
6 |
46,633 |
18,018 |
6,995 |
|
7 |
47,413 |
18,256 |
7,112 |
|
8 |
48,070 |
18,455 |
7,210 |
|
9 |
48,621 |
18,623 |
7,293 |
|
10 |
49,084 |
18,763 |
7,363 |
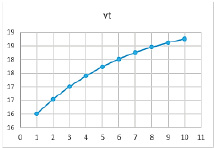
Рис. 18. Результат расчетов при значениях параметров α = 0,79, β = 0,4, γ = 0,8
Таблица 19
(для значений параметров α = 0,79, β = 0,8, γ = 0,4)
|
t |
PKt |
vt |
Dt |
|
1 |
0,000 |
16,000 |
0,000 |
|
2 |
59,391 |
21,812 |
5,120 |
|
3 |
81,923 |
28,121 |
8,192 |
|
4 |
106,713 |
34,653 |
10,671 |
|
5 |
132,676 |
41,158 |
13,268 |
|
6 |
158,792 |
47,435 |
15,879 |
|
7 |
184,212 |
53,339 |
18,421 |
|
8 |
208,295 |
58,776 |
20,829 |
|
9 |
230,610 |
63,697 |
23,061 |
|
10 |
250,912 |
68,088 |
25,091 |
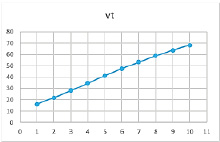
Рис. 19. Результат расчетов при значениях параметров α = 0,79, β = 0,8, γ = 0,4
Таблица 20
(для значений параметров α = 0,79, β = 0,8, γ = 0,8)
|
t |
PKt |
vt |
Dt |
|
1 |
0,000 |
16,000 |
0,000 |
|
2 |
109,230 |
35,297 |
5,120 |
|
3 |
244,496 |
66,709 |
12,225 |
|
4 |
468,558 |
111,519 |
23,428 |
|
5 |
793,491 |
169,077 |
39,675 |
|
6 |
1217,178 |
237,070 |
60,859 |
|
7 |
1724,460 |
312,178 |
86,223 |
|
8 |
2291,514 |
390,790 |
114,576 |
|
9 |
2891,164 |
469,563 |
144,558 |
|
10 |
3497,398 |
545,765 |
174,870 |
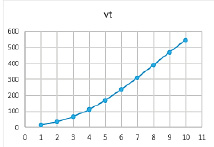
Рис. 20. Результат расчетов при значениях параметров α = 0,79, β = 0,8, γ = 0,8
Таблица 21
(для значений параметров α = 0,79, β = 0,9, γ = 0,8)
|
t |
PKt |
vt |
Dt |
|
1 |
0,000 |
16,000 |
0,000 |
|
2 |
206,251 |
58,320 |
5,120 |
|
3 |
753,957 |
162,387 |
18,849 |
|
4 |
2105,814 |
365,552 |
52,645 |
|
5 |
4755,206 |
695,682 |
118,880 |
|
6 |
9076,675 |
1159,335 |
226,917 |
|
7 |
15167,701 |
1739,296 |
379,193 |
|
8 |
22811,449 |
2400,975 |
570,286 |
|
9 |
31557,339 |
3102,674 |
788,933 |
|
10 |
40855,337 |
3804,813 |
1021,383 |
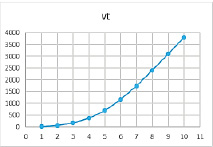
Рис. 21. Результат расчетов при значениях параметров α = 0,79, β = 0,9, γ = 0,8
Таким образом, влияние риска структуры капитала на динамику производственной сферы при нелинейной ставке по кредиту наиболее значимо для комбинаций параметров β = 0,9, γ = 0,8 и β = 0,9, γ = 0,4. Ниже наглядно показаны существенные различия линейной и нелинейной зависимостей для указанного набора параметров (отличия наблюдаются также по масштабу на оси ординат).
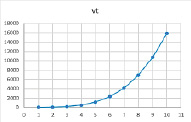
Рис. 22. Линейная зависимость при комбинации параметров β = 0,9, γ = 0,8
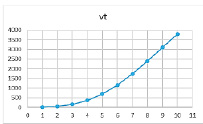
Рис. 23. Нелинейная (параболическая) зависимость при комбинации параметров β = 0,9, γ = 0,8
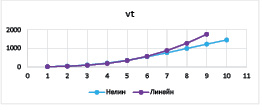
Рис. 24. Наложение линейной и нелинейной функции
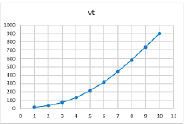
Рис. 25. Линейная зависимость при комбинации параметров β = 0,9, γ = 0,4
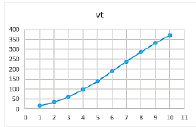
Рис. 26. Нелинейная(параболическая) зависимость при комбинации параметров β = 0,9, γ = 0,4
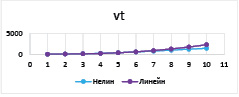
Рис. 27. Наложение линейной и нелинейной функции
Приведем комбинации управляемых параметров, при которых наблюдаются существенные отличия динамики для случаев линейной и нелинейной зависимости ставки кредита от структуры рабочего капитала.
Таблица 22
|
α |
β |
γ |
Динамика «выпуск-затраты» |
|
0,79 |
0,9 |
0,4 |
Квазилинейный рост |
|
0,9 |
0,8 |
Экспоненциальный рост |
В третьей части эмпирических исследований экономической динамики предприятия с неоклассической производственной функцией (степени однородности α = 0,79) представим результаты расчетов по динамической модели для варианта, при котором выплаты по кредиту фиксированы, а доля отчислений на непроизводственное потребление изменяется по интервалам планирования (с целью повышения дивидендных выплат и повышения инвестиционной привлекательности компании).
Для этого необходимо выделять не больше половины регулируемой доли γt из собственных средств Cst. Таким образом формула по расчету дивидендов будет иметь вид:
Dt = (1 – 0,5γt) · Cst.
Рассчитаем дивиденды по новой формуле и сравним с результатами до преобразований и после (таблицы 22,23) (зафиксируем β = 0,6).
Таблица 23
(для значений параметров α = 0,79, β = 0,6, γ = 0,8)
|
До преобразований |
После преобразований |
|||||||
|
t |
PKt |
vt |
Dt |
t |
PKt |
vt |
Dt |
|
|
1 |
0,000 |
16,000 |
0,000 |
1 |
0,000 |
16,000 |
0,000 |
|
|
2 |
61,471 |
22,413 |
5,120 |
2 |
61,471 |
22,413 |
15,360 |
|
|
3 |
87,458 |
29,612 |
8,746 |
3 |
87,458 |
29,612 |
26,237 |
|
|
4 |
117,148 |
37,303 |
11,715 |
4 |
117,148 |
37,303 |
35,144 |
|
|
5 |
149,360 |
45,195 |
14,936 |
5 |
149,360 |
45,195 |
44,808 |
|
|
6 |
182,861 |
53,030 |
18,286 |
6 |
182,861 |
53,030 |
54,858 |
|
|
7 |
216,509 |
60,600 |
21,651 |
7 |
216,509 |
60,600 |
64,953 |
|
|
8 |
249,346 |
67,752 |
24,935 |
8 |
249,346 |
67,752 |
74,804 |
|
|
9 |
280,638 |
74,385 |
28,064 |
9 |
280,638 |
74,385 |
84,191 |
|
|
10 |
309,874 |
80,442 |
30,987 |
10 |
309,874 |
80,442 |
92,962 |
|
Таблица 24
(для значений параметров α = 0,79, β = 0,6, γ = 0,4)
|
До преобразований |
После преобразований |
|||||||
|
t |
PKt |
vt |
Dt |
t |
PKt |
vt |
Dt |
|
|
1 |
0,000 |
16,000 |
0,000 |
1 |
0,000 |
16,000 |
0,000 |
|
|
2 |
30,736 |
12,962 |
15,360 |
2 |
30,736 |
12,962 |
20,480 |
|
|
3 |
24,674 |
10,897 |
14,804 |
3 |
24,674 |
10,897 |
19,739 |
|
|
4 |
20,594 |
9,447 |
12,356 |
4 |
20,594 |
9,447 |
16,475 |
|
|
5 |
17,751 |
8,401 |
10,651 |
5 |
17,751 |
8,401 |
14,201 |
|
|
6 |
15,714 |
7,630 |
9,428 |
6 |
15,714 |
7,630 |
12,571 |
|
|
7 |
14,219 |
7,050 |
8,531 |
7 |
14,219 |
7,050 |
11,375 |
|
|
8 |
13,101 |
6,609 |
7,860 |
8 |
13,101 |
6,609 |
10,481 |
|
|
9 |
12,251 |
6,267 |
7,350 |
9 |
12,251 |
6,267 |
9,801 |
|
|
10 |
11,596 |
6,001 |
6,958 |
10 |
11,596 |
6,001 |
9,277 |
|
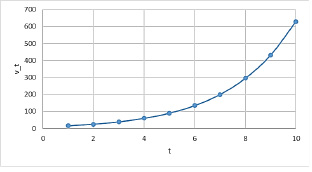
Рис. 28. Прогнозная динамика производства
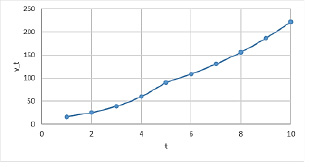
Рис. 29. Динамика производства после снижения темпов накопления
Таким образом, можно сделать вывод, что за счет проведенных преобразований в расчете размера дивидендов удалось без изменения других эндогенных параметров увеличить размер выплаты дивидендов в первом случае в 3 раза, во втором – в 1,5 раза.
Рассмотрим теперь случай, когда динамика производства непостоянна. При α = 0,75; γt = 0,8; βt = 0,6 прогнозная динамика производства имеет следующий вид (рисунок 28).
Выпуск растет экспоненциально на всём горизонте планирования, а, следовательно, есть возможность меньше инвестировать в производство и выплачивать больше дивидендов. На 6-м шаге, когда прогнозный выпуск должен превысить значение 100, снизим темп накопления собственных средств в производственном капитале с γt = 0,8 до γt = 0,6. Тогда динамика производства будет иметь следующий вид (рисунок 29):
На 6-м шаге наблюдается перегиб, и на каждом последующем шаге производство уменьшается примерно в три раза по сравнению с первоначальным планом. Однако, несмотря на уменьшения темпа накопления собственных средств в производственном капитале, продолжает наблюдаться возрастающий тренд, а, значит имеется возможность меньше инвестировать в производство и больше направлять на выплату дивидендов.
Результирующий вывод
Проведенные эмпирические расчеты по динамической модели производственной сферы предприятия убедительно демонстрируют актуальность постановки задачи оптимизации структуры производственного капитала предприятия на основе корректного определения управляемых параметров, в качестве которых предложено использовать темп накопления в производственном капитале собственных средств и коэффициент долга.

