Введение
В последние годы в России наблюдается рост уровня смертности, что влечет за собой естественную убыль населения, которая, в свою очередь, имеет негативные последствия, такие как ограничения экономического роста. Для того, чтобы эффективно разрабатывать стратегию развития отдельно регионов и страны в целом, необходимо иметь достоверный прогноз смертности.
Существует множество подходов к прогнозированию смертности, отличающихся прогнозируемыми показателями, методами прогнозирования и источниками информации. Выбор конкретного подхода зависит от вида, количества и качества имеющихся данных, постановки задачи, горизонта прогнозирования. Обычно в демографических исследованиях используют экстраполяционные, интерполяционные и мультикаузальные подходы к прогнозированию смертности. Рассмотрим их основные особенности, достоинства и недостатки.
Результаты исследования и их обсуждение
Экстраполяционные подходы
Экстраполяция является относительно простым и широко используемым на практике методом прогнозирования смертности. Она базируется на предположении о сохранении в прогнозном периоде сложившихся в прошлом закономерностей в динамике показателей смертности. Прогнозы показателей смертности обычно разрабатываются на основе трендовых моделей, построенных с использованием их значений, наблюдаемых в базисном периоде. Основными проблемами при реализации такого подхода являются обоснование длины базисного периода и временной функции, используемой для экстраполяции соответствующих ему закономерностей в динамике показателей смертности.
Подход Lee-Carter
В качестве примера модели, реализующей экстраполяционный подход, рассмотрим следующую зависимость, предложенную в 1992 г. Lee и Сarter [9, 21, 2] для прогнозирования возрастных показателей смертности:
ln qm,t = αm + βm · kt + εm,t , (1)
m = 1, …, M, t = 1, …, T
где qm,t – показатель смертности в возрастной группе m (m=1,…, M), M – номер последней возрастной группы, например, свыше 100 лет; (в период t (t =1,…,T) (Lee и Сarter рекомендуют использовать возможно больший базисный период). Параметр αm характеризует систематический риск смерти в возрастной группе m в базисном периоде (обусловленный естественными процессами старения), обычно за его оценку принимается среднее значение логарифмов коэффициентов смертности в возрастной группе m
.
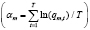Параметр βm отражает несистематический риск смерти в возрасте m в базисном периоде (обусловленный несчастными случаями, природными катаклизмами, заболеваниями и т. п.). Параметр kt характеризует эффект периода времени (развитие здравоохранения, ухудшение экологии и т.п.). εm,t – ошибка модели, предположительно распределенная по нормальному закону с нулевым математическим ожиданием и постоянной дисперсией.
Значения βm инвариантны ко времени. Значения kt для всех возрастных групп является постоянной величиной.
Параметры βm и kt должны быть оценены с помощью соответствующих методов, исходя из данных о возрастной смертности в базисном периоде. Lee и Сarter [2] предлагают метод сингулярного разложения матрицы центрированных логарифмов возрастных показателей смертности в базисном периоде (рис. 1).
Согласно теореме о сингулярном разложении для любой матрицы Q∈RM×T, rank(Q)=τ существует ее представление в виде произведения Q = U · D · V’.
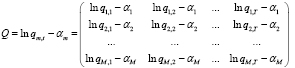
Рис. 1. Матрица центрированных логарифмов возрастных показателей смертности
При М > T схема разложения следующая:
,
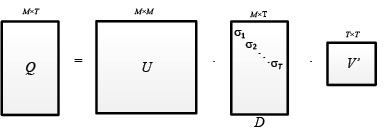при T >М
,
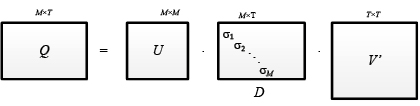где U∈RM×M, V∈RT×T – ортогональные матрицы; матрица D∈RM×T имеет ненулевыми только элементы djj = σj при j∈{1,…, τ}:
.
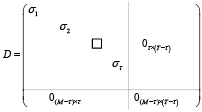Числа σ1, σ2,…, στ расположены в порядке убывания: σ1 ≥ σ2 ≥ … ≥ στ > 0 и равны модулям квадратных корней из ненулевых собственных чисел матрицы Q · Q’
,
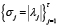где λ12, λ22,…, λτ2 – корни уравнения
det(Q · Q’ – λ2E) = 0
Столбцы матрицы U являются собственными векторами матрицы Q · Q’:
U = [U[1]| U[2]|…| U[M]],
при (Q · Q’ – λ2E) · U[j] = 0M×1
Столбцы матрицы V являются собственными векторами матрицы Q · Q’:
V = [V[1]| V[2]|…| V[T]],
при (Q · Q’ – λj2E) · V[j] = 0T×1
Согласно [2], в качестве оценок параметров 
принимаются элементы первого столбца матрицы U, а в качестве оценок 
– произведения элементов первого столбца матрицы V на максимальное сингулярное число σ1 из матрицы D. При этом на оценки параметров накладываются два ограничения:
, 
.
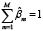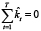Наряду с сингулярным разложением существует еще один подход к оценке параметров βm и kt , предложенный Girosi и King [14, 15] и Pedroza [30]. В качестве оценок параметров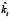 
принимаются суммы элементов столбцов матрицы Q = {lnqm,t – αm}. Параметры βm оцениваются методом наименьших квадратов. Для этого строятся зависимости центрированных логарифмов коэффициентов смертности в каждой возрастной группе в базисном периоде от оценок параметров 
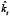(t = 1,…, T).
Оценки параметров модели Lee-Carter, полученные двумя методами, очень близки. Метод сингулярного разложения обеспечивает несколько лучшее качество аппроксимации коэффициентов смертности в конце базисного периода по сравнению с методом наименьших квадратов.
Преимущества модели Lee-Carter по сравнению с другими прогнозными моделями возрастной смертности состоят в ее относительно простой конструкции и устойчивости. Модель включает минимум параметров, каждый из которых можно демографически интерпретировать. Для их оценки требуется сравнительно небольшое количество информации. Кроме того, модель Lee-Carter охватывает основные тенденции возрастной смертности в базисном периоде.
Однако модель Lee-Carter также имеет и некоторые недостатки. Использование центрированных логарифмов показателей смертности может привести к искажениям оценок параметров модели; случайные скачки в исходных данных могут неправильно интерпретироваться как тенденции и, как таковые, встраиваться в модель. Кроме того, реальные изменения смертности варьируются в зависимости от возраста и времени. Модель же Lee-Carter учитывает только одно, для всех возрастов одинаковое, изменение смертности во времени с помощью параметра kt. При этом предполагается неизменный несистематический риск смерти для каждого возраста m на протяжении базисного и прогнозного периодов.
Редко выполняющееся на практике предположение о независимости возрастной и временной составляющих смертности ограничивает применение модели Lee-Carter в решении задач долгосрочного прогнозирования ее показателей. Чем больше прогнозный период, тем менее правдоподобным кажется это предположение. Модель больше подходит для построения краткосрочных прогнозов, разрабатываемых исключительно методами экстраполяции сложившихся в базисном периоде тенденций смертности и не учитывающих дополнительной информации о возможностях их изменения.
Отмеченные недостатки модели (1) в определенной степени устранены в ее модификациях [4, 5, 18-23, 39]. В частности, в 2007 г. Hyndman и Ullah модифицировали модель Lee-Carter путем использования в качестве исходных данных сглаженных уровней смертности базисного периода. Это позволило смягчить случайные выбросы в исходных данных, и, тем самым повысить достоверность тенденций их изменчивости в прогнозном периоде. Согласно предложенной ими модификации модель (1) имеет следующий вид:
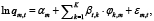(2)
m = 1, …, M, t = 1, …, T
При этом базовые функции φk,m отражают смертность в k-й совокупности возрастов. Эффект периода времени для k-й совокупности возрастов отражают показатели βt,k.
Известны модификации модели (1), которые описывают динамику показателей смертности по ее различным причинам [10, 15, 44].
Законы смертности
Закон смертности отражает эмпирическое возрастное распределение смертности с помощью математической функции. Количество параметров функции варьируется от 2 до 9. При разработке закона смертности обычно учитывают 2 условия. С одной стороны, закон смертности должен обеспечивать высокое качество приближения модельных значений к фактическим данным. С другой стороны, параметры модели должны быть демографически интерпретируемыми [37].
В качестве исходных данных при прогнозировании возрастных показателей смертности на основании закона распределения используются законы, адекватно отражающие такие распределения в базисном периоде. При этом закон распределения на момент прогноза определяется на основе прогнозных оценок его параметров с использованием в качестве исходных данных их значений, имевших место в базисном периоде.
Попытки описать динамику смертности и ее возрастного распределения математическими функциями предпринимались, начиная с первой половины XVIII века [16, 17, 28, 32, 38].
В частности, Gompertz [16], предложил закон, основанный на предположении, что с возрастом смертность увеличивается в геометрической прогрессии:
qm = B · cm. (3)
Из выражения (3) следует, что вероятность смерти q в возрасте m по Gompertz объясняется двумя константами, с одной стороны, общей вероятностью смерти (В), а, с другой стороны, физическим вырождением (c), увеличивающимся с возрастом m [40]. При формулировке этого закона смертности Gompertz исследовал возрастную смертность взрослого населения Швеции. Этот закон достаточно достоверно описывает динамику смертности в зрелых возрастах (что связано с его внутренним предположением об экспоненциальном росте смертности с возрастом), чего нельзя сказать о младенческой и детской смертности. Существует и верхняя граница использования закона Gompertz, так как смертность в старших возрастах растет не в геометрической прогрессии, а несколько медленнее. Статистика смертности в ряде стран свидетельствует, что выражение (3) соответствует распределению ее показателей в возрастных группах от 25 до 75 лет, хотя сам автор указывал на диапазон от 20 до 60 лет [47, 32].
В 1872 году Thiele предложил моделировать закон смертности во всех возрастах как сумму трех слагаемых, отличающихся для детей, лиц среднего и старшего возрастов. Heligman and Pollard [17] в 1980 г. и Rojers and Little [34] в 1994 г. с учетом этого предложения сформулировали два следующих уравнения, описывающие возрастные распределения смертности. Согласно Heligman and Pollard, выражение закона смертности, включающее три слагаемых и восемь параметров имеет следующий вид:
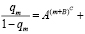
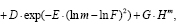(4)
где qm вероятность смерти в возрасте m.
Первое слагаемое описывает смертность в детских возрастах (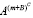
), параметр С является отрицательным, обеспечивая быстрое снижение первого слагаемого с возрастом. Последнее слагаемое (G · Hm) похоже на логистическую кривую и описывает смертность в старших возрастах. Среднее слагаемое 
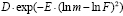учитывает всплеск смертности в возрастном интервале 20-45 лет. Все восемь параметров модели могут быть демографически интерпретированы.
Мультиэкспоненциальная модель Rogers и Little включает пять слагаемых и 13 параметров. Особенность этой модели состоит в ее общей формулировке, которая позволяет гибко моделировать различные демографические показатели (в т.ч. рождаемость, смертность и миграцию). В зависимости от того, какие параметры модели принимают (или не принимают) нулевое значение, могут строиться U-образные, одно- и двухвершинные распределения. В частности, для моделирования смертности используются четыре компонента и 9 параметров. При этом не каждый из 9 параметров модели можно демографически интерпретировать [3, 24, 25].
Вместе с тем попытки описать возрастные распределения показателей смертности с помощью функций, содержащих большее число параметров, на практике не приводят к повышению достоверности результатов. При этом процедура построения законов смертности сложнее, чем у стандартных прогнозных моделей. В связи с этим законы смертности редко используются при прогнозировании ее возрастных распределений.
Реляционная модель Brass
Реляционная модель смертности Brass, разработанная в 1968-1971 гг. [6, 7], отражает зависимость logit-преобразований показателей таблицы смертности Ym от logit-преобразования стандартных (модельных) показателей Ym*. Ym* определяются на основе стандартной (модельной) таблицы смертности, отражающей изменение интенсивности смертности с изменением возраста для населения со сходным порядком вымирания и представляющей собой обобщение эмпирических таблиц, относящихся к более или менее одинаковым возрастным закономерностям смертности.
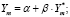(5)
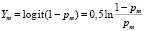, (6)
где pm – вероятность дожития до возраста m.
Для построения линейной функциональной связи (5) необходимо оценить два параметра модели, α и β.
Logit-преобразования возрастных показателей смертности для каждого наблюдения в базисном периоде описываются моделью Brass. Формируются временные ряды оценок параметров модели, которые затем экстраполируются с помощью подходящей модели временного ряда. Прогнозные значения параметров подставляются в модель Brass, и на этой основе строится прогноз logit-преобразований показателей смертности. В качестве стандартных показателей смертности в прогнозном периоде Brass предложил использовать фактические показатели смертности в последнем году базисного периода.
Реляционная модель Brass является относительно простой моделью, отражающей связь показателей смертности исследуемого и «стандартного» населений с помощью двух параметров. Но чем больше отклонение наблюдаемых показателей смертности от стандартных, тем менее правдоподобным выглядит предположение об их линейной связи.
Age-Period-Cohort модель
Age-Period-Cohort модель (сокращенно APC) представляет собой регрессионную модель, отражающую влияние на логарифм показателя смертности трех факторов: возраста, периода и когорты. Однако параметры этой модели не могут быть однозначно идентифицированы [12, 37]. APC-модель редко используются для прогнозирования смертности, тем не менее она применяется в эпидемиологии для анализа смертности от отдельных причин [10, 12].
Подходы, учитывающие целевые распределения смертности
Согласно этим подходам возрастное распределение смертности в конкретном году (целевое распределение) задается априори. Различия между отдельными вариантами таких подходов заключаются в способах формирования целевого распределения смертности (с помощью экстраполяции, интерполяции, экспертных оценок или путем комбинации перечисленных методов). Рассмотрим некоторые из этих вариантов более подробно.
Смертность «продвинутого» населения как эталон
Этот подход основан на предположении, что уровни смертности исследуемого населения развиваются до уровней смертности продвинутого населения в соответствии с некоторыми закономерностями.
Для применения этого подхода необходимо сначала выбрать подходящее продвинутое население, а также определить «расстояние» между смертностью исследуемой и продвинутой популяции. Для этого могут быть проанализированы социально-экономические и культурные факторы, а также развитие медицины и основные причины смерти. После этого рассматривается траектория развития смертности. Точных методов ее определения не существует. В качестве прогноза смертность исследуемого населения может использоваться, например, фактическая смертность продвинутого населения, реализующаяся с запаздыванием во времени. Может также проводится интерполяция между начальным и целевым распределениями смертности [31, 35].
Практическая реализация этого подхода к прогнозированию смертности создает некоторые проблемы. У исследователя отсутствует точная процедура прогнозирования. Выбор подходящего продвинутого населения весьма сложен. Не менее трудным является определение периода запаздывания между реализацией одинаковых распределений смертности. Эта проблема еще больше усиливается различными причинами, существенно влияющими на развитие смертности в обеих популяциях. Преимуществом подхода можно считать возможность косвенного учета дополнительной информации (например, медицинской).
Таблица оптимальной смертности в качестве эталона
В качестве целевого распределения смертности для рассматриваемого населения может использоваться так называемая «таблица оптимальной смертности». С этим подходом связан вопрос о том, насколько сильно действительно может уменьшиться смертность в каждом возрасте.
При этом подходе формируется таблица оптимальной смертности в предположении о максимально возможном снижении смертности. Так таблица оптимальной смертности может исходить, например, из возрастных распределений вероятностей смерти в странах с самой низкой смертностью. После выявления оптимального целевого распределения смертности для рассматриваемого населения, с помощью соответствующего метода (например, интерполяции) определяется траектория снижения уровней смертности от фактического к целевому распределению [31].
Мультикаузальные подходы
Прогноз смертности с учетом долголетия
Учет долголетия при прогнозировании возрастных показателей смертности связывается с оценкой влияния на их значения ожидаемой продолжительности жизни. При этом в отношении ее величины мнения специалистов расходятся. Одна группа исследователей, при прогнозировании смертности опирающаяся на аргументы эволюционной биологии, считает, что увеличение ожидаемой продолжительности жизни при рождении свыше 85 лет маловероятно в отсутствие сенсационных медицинских открытий и вмешательства в процесс старения человека. Эти исследователи предполагают даже сокращение будущей продолжительности жизни при рождении из-за современных тенденций в здоровье населения (например, ожирения населения промышленно развитых стран) [8, 29]. Другая группа ученых, занимающаяся обработкой эмпирических данных по смертности, предполагает сохранение тенденции к увеличению продолжительности жизни, наблюдаемой в прошлом [43]. Эмпирики считают возможным увеличение ожидаемой продолжительности жизни при рождении свыше 100 уже в этом веке [26]. Представители двух течений согласны, что в будущем смертность в старости может снизиться, но расходятся в своих предположениях о степени, скорости и основных процессах ее снижения.
Эмпирики при прогнозировании смертности предполагают, что наблюдаемые в прошлом тенденции увеличения продолжительности жизни сохранятся [26, 40, 41, 42]. Так, в странах с самой низкой смертностью за последние 160 лет ожидаемая продолжительность жизни при рождении росла линейно (на 3 месяца в год или на 2,5 года за десятилетие). Сохранение этой тенденции увеличит ожидаемую продолжительность жизни при рождении до 100 лет в течение ближайших шестидесяти лет. Рост ожидаемой продолжительность жизни при рождении, начиная с 1950 г. был вызван, а с 1970 г. усилен в значительной степени снижением уровня смертности в пожилом возрасте (свыше 80 лет) в основном за счет биомедицинских достижений. Эмпирики выступают как против бессмертия, так и против (очевидного) верхнего предела ожидаемой продолжительности жизни при рождении. Их предположения основываются на наблюдаемой долгосрочной линейной тенденции, приводящей к тому, что недавно установленный предельный уровень ожидаемой продолжительности жизни достигался и превышался. Еще одно подтверждение своих предположений эмпирики находят в отсутствии корреляции между уровнем смертности и степенью ее снижения. Если бы корреляция существовала, то снижение смертности в странах, близких к верхнему пределу ожидаемой продолжительности жизни при рождении, должно быть меньше, чем в странах, далеких от этого предела. Поэтому прогнозы смертности, предполагающие замедленное снижение смертности, а также предельный уровень продолжительности жизни оценивается эмпириками как необоснованные.
Ученые, рассматривающие аргументы эволюционной биологии, считают экстраполяцию прошлого развития смертности математически правильной, но (эволюционно) биологически неоправданной [28]. Они предполагают, что бессмертие не заложено в геноме человека. Старение человека является побочным продуктом эволюции, поддерживающей в процессе естественного отбора гены здоровья и жизнеспособности для достижения половой зрелости, репродукции и выращивания потомства. Следовательно, старение эволюцией не предусмотрено, поэтому ожидаемая продолжительность жизни при рождении не может стать бесконечной даже при отсутствии смертельных угроз со стороны окружающей среды и вследствие медицинского вмешательства [8, 27]. Представители этой точки зрения при прогнозировании смертности исходят из того, что будущее развитие смертности отличается от прошлого и настоящего развития. Они обосновывают это предположение путем сравнения сокращения смертности в разных возрастных группах в ХХ веке. В то время как в первой половине увеличение продолжительности жизни при рождении в основном шло как следствие снижения младенческой и материнской смертности, во второй половине оно было обеспечено сокращением дегенеративных заболеваний в старости. Будущее развитие смертности может отличаться от прошлого и настоящего развития, поскольку найдены возможности вмешательства в процесс старения человека [1]. Однако являются ли достижения в генной инженерии шагом к существенному увеличению ожидаемой продолжительности жизни при рождении, пока непонятно [29].
В последние десятилетия самое большое снижение смертности происходит в старших возрастах, однако этот процесс оказывает гораздо меньшее влияние на ожидаемую продолжительность жизни при рождении, чем (такое же абсолютное) снижение смертности в молодых возрастах. Специалисты приводят этот довод в пользу замедления роста ожидаемой продолжительности жизни при рождении, если он не ускорится новым революционным открытием. Соответственно, экстраполяция долгосрочных тенденций продолжительности жизни представляется слишком оптимистичной.
Дискуссия о долголетии, связанная, в частности, с расшифровкой генома человека набирает обороты. В отсутствие надежной дополнительной информации из смежных областей знаний, прогнозы смертности могут основываться только на ее динамике. Однако Pritchett [33] уже в 1891 г. заметил, что не нужно преувеличивать качества такого прогноза, потому что в момент его построения не совсем понятны будущие условия развития смертности.
Прогноз смертности с учетом причин смерти
Динамика общих показателей смертности является относительно стабильной и регулярной, однако в разное время она определяется различными основными причинами смерти [45]. В таких ситуациях прогнозирование показателей смертности как суммы ее уровней, обусловленных различными причинами, может привести к более точным результатам.
Результаты прогнозирования смертности в соответствии с таким подходом не будут искажаться неоднородностью причин, потому что каждая причина смерти рассматривается отдельно, а затем прогнозируется общая смертность.
Тем не менее, при реализации причинного подхода могут возникнуть некоторые проблемы. Динамика показателей смертности по причинам смерти менее стабильна и регулярна, чем динамика показателей общей смертности [44, 45]. Постоянный пересмотр международной единой системы классификации причин смерти и болезней затрудняет последовательный анализ смертности по причинам смерти с течением времени, так как с выходом новой редакции ICD (ICD – Inernational Classification of Diseases and Related Health Problems) болезни могут по-другому кодироваться или добавляться новые [13, 31, 36]. Кроме того, причины смерти не всегда указываются правильно. В медицинском свидетельстве о смерти врач должен проанализировать причинно-следственную цепь от основной болезни до причины, непосредственно приводящей к смерти. Первая некорректность может быть результатом неправильного медицинского диагноза; он особенно затруднен в случае смерти в пожилом возрасте из-за относительно высокой распространенности сочетания болезней, а обычно указывается только одна причина.
Дополнительные проблемы могут быть связаны с неправильным кодированием основного заболевания в соответствующей статистике. Для того чтобы этого хотя бы частично избежать, указываются только основные причины смерти, такие как болезни системы кровообращения или новообразования. Но даже при условии, что все причины смерти были должным образом зарегистрированы, существует проблема так называемых «конкурирующих рисков». Эта проблема приводит к искажению результатов прогнозирования общей смертности на основе независимых прогнозов смертности по отдельным причинам смерти, потому что в реальности причины смерти не являются независимыми [2, 5, 45, 46].
Прогноз общей смертности в виде суммы прогнозов смертности по отдельным причинам не всегда оказывается точнее, чем чистый прогноз общей смертности. В прогнозном периоде могут произойти неожиданные изменения тенденций, которые сильнее затронут смертность по отдельным причинам. Предвидеть изменения тенденций можно только с учетом предположений о демографическом поведении и медицинских инновациях, методах лечения [45].
Исследование Caselli [10] показывает, что экстраполяция общей смертности как суммы показателей смертности по причинам смерти вообще не дает существенных преимуществ по сравнению с чистым прогнозом общей смертности. Прогноз общей смертности как суммы смертности по причинам смерти оказывается более пессимистичным, чем чистый прогноз общей смертности [10, 13, 44, 45].
В заключение следует отметить, что прогноз смертности с учетом причины смерти только тогда дает лучший результат, когда меняется структура причин смерти, и эти изменения могут быть отражены параметрами модели. В остальных случаях прогноз смертности с учетом причин смерти недостаточно надежен из-за его повышенной сложности. Он не обеспечивает ни методических, ни содержательных преимуществ над экстраполяцией смертности, если решающим критерием является точность прогноза.
Прогноз смертности по причинам смерти на текущем методическом уровне больше подходит для целей краткосрочного прогнозирования, потому что для короткого горизонта более вероятно сохранение наблюдаемых тенденций [2].
Байесовские подходы
Байесовские подходы позволяют гибко подходить к прогнозированию показателей смертности с учетом различных объясняющих переменных в условиях неопределенности. При построении модели может приниматься во внимание качественная и количественная информация из различных источников, которая аккумулируется в априорном распределении. При этом информация из имеющихся данных (likelihood) дополняется субъективными экспертными оценками (aprior). После введения предположений в уравнение модели получаются прогнозы показателя смертности в виде апостериорного распределения (aposterior):
aposterior ∼ likelihood · aprior. (7)
Байесовские подходы к прогнозированию повозрастной смертности использовали Girosi и King [14, 15] и Pedroza [30].
Байесовские подходы представляют собой удачный симбиоз количественной и качественной информации. Это позволяет интегрировать в прогноз практически всю доступную информацию и субъективные предположения. Тем не менее, процедуры реализации байесовских подходов методически достаточно сложны, что связано с использованием относительно большого количества исходной информации.
Заключение
Ключевые отличия рассмотренных подходов к прогнозированию смертности определяются характером используемой информации. Экстраполяционные подходы предполагают сохранение тенденций базисного периода в развитии показателей смертности. Интерполяционные, мультикаузальные и байесовские подходы предполагают также использование качественной (или субъективной) информации. Для интерполяции, по крайней мере, субъективно должно быть определено целевое распределение смертности. Траектория развития от начального до целевого распределения определяется на основе математической интерполяции. В мультикаузальных подходах теоретические положения смежных научных областей могут быть интегрированы в прогноз смертности с целью корректировки тенденций, наблюдаемых в прошлом. В связи с байесовскими подходами должно быть принято во внимание соответствующее распределение вероятностей значений факторов, объясняющих динамику смертности.
Таким образом, можно сделать вывод, что основой высококачественных прогнозов смертности и ее возрастных распределений являются, во-первых, достоверная исходная информация об уровнях ее показателей в прошлые (базисные) периоды времени и (если возможно) о тенденциях и причинах изменчивости смертности в прогнозный период.