Введение
Интенсивное развитие рыночной экономики в условиях санкций обусловило появление новых и активизацию ранее существующих форм хозяйственных отношений между производителями и потребителями продукции и услуг. Одной из таких форм является работа предприятия по заказам. При планово-командной системе управления экономикой заказ спускался предприятию вышестоящими организациями. При этом сроки выполнения заказа, его финансирование, обеспечение производственными ресурсами устанавливались на уровне министерств и ведомств. В том числе и организация сбытовой деятельности в условиях работы по заказам выходила за рамки задач, решаемых на предприятии. Предприятию необходимо было, руководствуясь требованиями, предъявляемыми к заказу, организовать и осуществить процесс производства. В современных условиях рыночной экономики все задачи, возникающие при работе по заказам, машиностроительному предприятию приходится решать самостоятельно. Одной из основных задач, оказывающих влияние на ход осуществления производственно-хозяйственной деятельности, является планирование работ, начиная, от поступления заказа на предприятие и рассмотрения выгодности его изготовления и, заканчивая, его реализацией заказчику, в предусмотренные для этого сроки.
Для повышения конкурентоспособности машиностроительного предприятия в условиях работы по заказам особое внимание следует уделить формированию оптимального плана реализации заказов потребителям [1].
Цель исследования заключается в формировании экономико-математической модели организации эффективной сбытовой деятельности машиностроительного предприятия, работающего по заказам.
Материалы и методы исследования
Для построения модели используется системный подход, согласно которого, планирование работы по заказам представляют, как сложную систему, состоящую из взаимосвязанных элементов. В качестве элементов, при разработке модели планирования деятельности машиностроительного предприятия по заказам, рассматриваются плановые работы, включающие процедуры определения выгодности поступающего заказа на предприятие, включения выгодного заказа в портфель заказов, формирования и корректировки производственной программы выпуска продукции и составления плана реализации заказов потребителям. Все эти элементы находятся в постоянном взаимодействии, что способствует быстрому пересмотру плановых показателей в связи с изменениями, происходящими как внутри самого машиностроительного предприятия, так и за его пределами. В результате взаимодействия во времени все элементы претерпевают количественные и качественные изменения, что позволяет говорить о планировании деятельности машиностроительного предприятия как о динамической системе.
Результаты исследования
и их обсуждение
Основным и наиболее трудоемким этапом планирования деятельности машиностроительного предприятия по заказам является разработка процедур формирования и корректировки производственной программы выпуска продукции и составления плана реализации заказов потребителям.
Рассмотрение двух этапов оперативного планирования в едином контексте обусловлено необходимостью составления согласованных планов производства и сбыта, для обеспечения более эффективной деятельности машиностроительного предприятия. Особенно большое значение взаимосвязь планов производства и сбыта приобретает для предприятия работающего по заказам. Насколько последовательно в этих планах будет воплощена идея своевременного выполнения заказов, зависит результативность производственно-хозяйственной деятельности машиностроительного предприятия.
Для реализации формирования и корректировки производственной программы выпуска продукции и составления плана реализации заказов потребителям разработана экономико-математическую модель планирования деятельности машиностроительного предприятия по заказам. Экономико-математическая модель учитывает ограниченность производственных ресурсов на предприятии, возможность несвоевременного выполнения заказов и применения по этой причине штрафных санкций, а также способность оборудования на разных операциях производить обработку различных видов изделий в целях более полной их загрузки. Экономико-математическая модель содержит ряд параметров, характеризующих состояние и структуру моделируемого объекта, а, именно, пооперационную трудоемкость изготовления изделия, объем производственных ресурсов на период планирования, структуру и объем запасов готовой продукции на складе предприятия, ассортимент заказов и требуемый объем по изделиям, стоимость и сроки выполнения заказов. Для более адекватного отражения процессов производства и реализации заказов, экономико-математическая модель планирования является динамической, то есть учитывает фактор времени, оптимизационной, то есть позволяет получить эффективный план из всех возможных, и управляемой, то есть способна реагировать на внешние воздействия менеджеров. В состав экономико-математической модели, удовлетворяющей всем вышеперечисленным характеристикам, входят целевая функция и ограничения-неравенства, описывающие область допустимых решений.
Целевая функция дает возможность сформировать оптимизационную экономико-математическую модель, позволяющую найти наиболее эффективное решение из всех допустимых вариантов. Для решения вопроса о виде целевой функции в модели планирования сбыта необходимо выбрать критерий оптимальной деятельности предприятия в условиях работы по заказам. Выбор критерия оптимальности можно сделать только на основе качественного анализа изучаемого экономического явления.
Деятельность любого машиностроительного предприятия, в том числе работающего по заказам, можно считать эффективной, если в результате ее осуществления удается вывести предприятие на иной, качественно или количественно более высокий, уровень развития. Экономическими показателями, характеризующими уровень развития предприятия, могут выступать: размер активов, величина собственного капитала, уровень дивидендов, котировка акций предприятия, рентабельность, ликвидность, платежеспособность и так далее. Однако, так или иначе, на значения этих показателей оказывает влияние универсальный экономический показатель называемый «прибыль». Прибыль является основным собственным источником развития предприятия. Этим объясняется стремление предприятия к получению наибольшей прибыли от осуществления производственно-хозяйственной деятельности. При работе машиностроительного предприятия по заказам, максимизировать прибыль можно только увеличением количества принятых к исполнению заказов. Ограниченность производственных и трудовых ресурсов приводит к тому, что машиностроительное предприятие может не выдерживать сроки выполнения, предусмотренные заказами, что приведет к появлению штрафных санкций, снижающих размер запланированной прибыли.
Таким образом, работающее по заказам машиностроительное предприятие, стремясь максимизировать прибыль от их выполнения, должно так сформировать план сбыта, чтобы минимизировать штрафные санкции при несвоевременном выполнении заказов [2].
Для математической формализации критерия оптимальности рассматривается динамика штрафных санкций при несвоевременном выполнении заказов, имеющая вид:
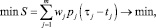(1)
где wj – размер пени за каждый день просрочки j-го заказа, в долях; pj – стоимость j-го заказа, руб.; τj – плановый срок выполнения заказа; tj – требуемый срок выполнения j-го заказа, дн.; m – количество заказов, участвующих в разработке планов.
При данном виде целевой функции процесс планирования будет осуществляться до тех пор, пока не будут определены плановые сроки сбыта всех заказов, формирующих портфель.
Построение ограничений экономико-математической модели дает возможность сформировать область допустимых решений задачи определения оптимального плана сбыта продукции машиностроительного предприятия. Всю совокупность ограничений, используемых для формирования экономико-математической модели, можно разделить на ряд функциональных блоков, описывающих определенный этап производственно-хозяйственной деятельности предприятия. Прежде чем приступить к описанию блоков ограничений, введем в рассмотрение два элемента, характеризующие цель экономико-математического моделирования. Целью является определение плана реализации заказов. Пусть вектор-столбец θ = [τj]m определяет плановый срок выполнения j-го заказа, а производственная матрица X = [xij]n×m – плановый объем выпуска изделия i-го вида к τj моменту времени.
Тогда, технологический блок ограничений можно представить в матричной форме как:
A•X ≤ F, (2)
где A = [aki]s×n – технологическая матрица, определяющая трудоемкость производства изделия i-го вида на k-й операции; F = [fkj]s×m – матрица фондов времени работы оборудования на k-й операции за период [0, τj].
В экономико-математической модели необходимо предусмотреть, чтобы плановый срок выполнения j-го заказа τj не мог быть меньше требуемого срока tj, то есть должно соблюдаться m-ограничений-неравенств вида: τj ≥ tj,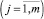 
. В матричной форме это условие примет вид:
θ ≥ T, (3)
где T = [tj]m – вектор-столбец, определяющий требуемый срок выполнения j-го заказа.
Технологический блок ограничений, состоящий из (s + 1)•m-ограничений-неравенств, описывает технологический процесс производства изделий на предприятии и позволяет так сформировать область допустимых решений, чтобы оптимальный план производства изделий по времени не вышел за допустимые размеры пооперационных фондов времени работы оборудования.
Ресурсный блок ограничений позволяет учесть в экономико-математической модели ограниченный размер сырья, материалов и других производственных запасов на предприятии. В матричной форме ресурсный блок ограничений можно записать:
B•X ≤ Q, (4)
где B = [bli]h×n – нормативная матрица расхода производственного запаса l-го вида на изделие i-го вида; Q = [qlj]h×m – матрица материальных ресурсов l-го вида за период [0, τj].
Ресурсный блок ограничений состоит из h×m-ограничений-неравенств, формирующих область допустимых решений таким образом, чтобы оптимальный план производства изделий, по величине затрачиваемых на это материальных ресурсов, не вышел за имеющиеся размеры производственных запасов.
Для построения блока ограничений, описывающих формирование запасов изделий на складе предприятия, введем в рассмотрение следующие элементы: Z = [zij]n×m – матрица запасов изделий i-го вида к τj моменту времени;
Z0 = [z0i]n – вектор-столбец запасов изделий i-го вида к началу планирования; D = [1j]m – вектор-строка с единичными элементами; R = [rij]n×m – реализационная матрица, определяющая объем реализации изделия i-го вида, входящего в заказ, к τj моменту времени.
Тогда ограничения-равенства, описывающие динамику запасов изделий на складе предприятия, будут в матричной форме иметь следующий вид:
Z = Z0•D + X – R. (5)
Число ограничений-равенств, входящих в блок ограничений, описывающих формирование запасов изделий на складе предприятия, определяется величиной n×m.
Рассмотрим еще один блок ограничений, участвующий в построении экономико-математической модели планирования. Это сбытовой блок ограничений, состоящий из n×m-ограничений-равенств, позволяющих определить значения элементов реализационной матрицы R, и n×m-ограничений-неравенств, формирующих область допустимых решений. Ограничения, входящие в сбытовой блок, представим в матричной форме:
– ограничения-равенства:
R = Y•U, (6)
где Y = [yij]n×m – ассортиментная матрица, определяющая требуемые объемы реализации изделий i-го вида в j-м заказе; U = [uij]m×m – квадратная матрица управления реализацией i-м заказом к τj моменту времени. Каждый элемент матрицы управления U может принимать только два альтернативных значения либо нуль, либо единица. Если uij = 0, то считают, что i-й заказ к τj моменту времени не выполнен, и, наоборот, если uij = 1, то – выполнен.
– ограничения-неравенства:
Y ≤ Z. (7)
Последние ограничения-неравенства позволяют таким оптимальным способом выявить сроки выполнения заказов, чтобы требуемый объем реализации по каждому изделию, входящему в заказ, покрывался запасом этого изделия на складе предприятия.
Экономико-математическая модель сбытовой деятельности предприятия, работающего по заказам, позволяющая оптимально сформировать план реализации заказов потребителям, может быть представлена в виде схемы (рисунок), включающей целевую функцию и систему ограничений, определяющих область допустимых решений [3].
В результате использования этой модели плановым работникам удается составить обоснованный план сбыта заказов. Полученный симплекс-методом, вектор-столбец θ = [τj]m является планом выполнения заказов для отдела сбыта предприятия. В этом плане определены сроки формирования того или иного заказа требуемыми объемами необходимых изделий со склада предприятия и его отправки потребителю.
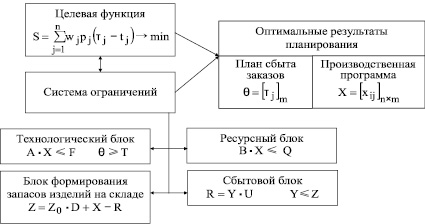
Схема экономико-математической модели сбытовой деятельности
машиностроительного предприятия, работающего по заказам
Найдем с помощью симплекс-метода производственную матрицу X = [xij]n×m, которая является производственной программой для машиностроительного предприятия, занимающегося выпуском изделий, участвующих в составлении заказов. Скорректировав матрицу
X = [xij]n×m, можно получить производственную программу для каждого вида изделия за периоды времени равные интервалам между выполнениями заказов.
Выводы
Таким образом, согласованное осуществление полученных планов производства и сбыта заказов, позволит проводить предприятию оптимальную производственно-сбытовую деятельность в условиях работы по заказам, то есть выплачивать минимальный размер штрафных санкций за несвоевременное выполнение заказов, а, значит, получать максимальную прибыль от этих хозяйственных операций.
Однако, несоблюдение, по той или иной причине, плана производства или сбыта заказов приведет к их рассогласованию, что потребует проведения новых плановых работ с использованием построенной экономико-математической модели. Любые изменения, происходящие на предприятии, за период планирования (поступление новых заказов, в составе производственных ресурсов, в объеме материальных запасов и т. п.) должны быть отражены в планах производства и сбыта. Для этого также необходимо пересчитать планы, после того как будут внесены соответствующие изменения в данные экономико-математической модели.