Информационно-программные технологии современных исследований достигаются прежде всего с помощью формализованного представления изучаемого объекта в виде математических моделей программно реализуемых на программном продукте в составе автоматизированных систем анализа. Этому способствует также применение формализованных моделей принятия решений, предполагавших использование разными моделями исследуемых объектов.
Повышение уровня научных исследований и оперативности получения результатов требует комплексного и активного использования симплексного метода задач линейного программирования, а также исследования операций и принятия решений на основе системного подхода и математического моделирования [3] с включением информационно-программных технологий процесса исследования.
Модель принятия рационального выбора содержит критерии оценивания предпочтительности сравниваемых вариантов решения и выделения среди них рационального варианта. Она ориентируется на многовариантный подход к формированию сравниваемых решений и использование принципа компромисса для выбора рационального варианта среди недоминируемых вариантов решений.
Реальным инструментом подготовки решений и рекомендаций по снижению затрат на мероприятия военного строительства стал симплексный метод, который впервые был описан профессором С.Ф. Викуловым в военно-экономическом анализе для применения в ВС РФ.
На его основе созданы специальные организационные структуры центрального и войскового звена управления военной организацией Российской Федерации, которые систематически выполняют исследовательские работы по различным видам анализа (анализ хозяйственной деятельности, технико-экономический анализ и т. д.), а также проводится оценка эффективности применения программ по расчету и контролю военных расходов на оборону государства.
В то же время до сих пор такие понятия, как военно-экономическая эффективность, военно-экономический анализ остаются объектами научных дискуссий. Необходимость комплексной оценки эффективности военно-экономического обеспечения безопасности России обусловлена возникновением новых внешнеполитических и макроэкономических условий функционирования военной организации России в начале XXI в. [4].
В условиях жестких бюджетных ограничений, которые являются скорее правилом, чем исключением, и характерны для всех времен и государств, уровень боевой готовности войск (сил) все больше становится зависимым не только от объема ресурсов, выделяемых на оборону и безопасность страны, но и от эффективности их использования [2].
Наиболее универсальным является так называемый симплексный метод (метод последовательного улучшения плана). Симплексный метод позволяет найти решение любой задачи линейного программирования, имеющей решение, проделав определенное число шагов, на каждом из которых выполняется по установленным правилам алгебраические преобразования. Истоки симплексного метода и его суть.
Впервые симплексный метод был предложен американским ученым Дж. Данцигом в 1949 г., однако еще в 1939 г. идеи метода были разработаны российским ученым Л.В. Канторовичем.
Симплексный метод, позволяющий решить любую задачу линейного программирования, универсален. В настоящее время он используется для компьютерных расчетов, однако несложные примеры с применением симплексного метода можно решить и вручную. Рассмотрим задачу линейного программирования симплексного метода решения задачи линейного программирования
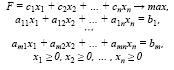(4)
В ней имеется n переменных и m независимых линейных ограничений-равенств. Введем понятие системы с базисом. Известно, что m линейно независимых уравнений (4) всегда можно разрешить относительно каких-то m переменных, выразив их через остальные k = n – m переменные.
Линейная система уравнений называется системой с базисом, если в каждом уравнении содержится переменная с коэффициентом, равным единице, отсутствующая во всех других уравнениях (т. е. входящая в эти уравнения с коэффициентом 0). Такие переменные называются базисными, остальные – свободными. Совокупность базисных переменных образует базис системы. Число базисных переменных очевидно, равно числу независимых уравнений. Система с базисом всегда совместна, так как она обладает, по крайней мере, одним решением, а именно, если положить свободные переменные равными нулю, то базисные переменные окажутся равными свободным членам соответствующих уравнений. Полученное таким образом решение называется базисным.
Среди различных базисных решений могут быть такие, которые дают отрицательные значения некоторых переменных. Это имеет место, когда некоторые свободные члены соответствующих уравнений отрицательны. Такие базисные решения противоречат условию не отрицательности переменных задачи линейного программирования и являются недопустимыми. Допустимым базисным решением является такое базисное решение, которое дает неотрицательные значения базисных переменных. Любому допустимому базисному решению соответствует вершина многогранника допустимых решений (опорная точка), определенного с помощью системы ограничений – равенств и условий не отрицательности переменных. Решение задачи линейного программирования, обращающее в максимум целевую функцию F, обязательно лежит среди допустимых базисных решений.
Если нам известны какая-то вершина и значение целевой функции в ней, то все те вершины, в которых целевая функция принимает худшее значение (т. е. меньшее в случае задачи на максимум и большее в случае задачи на минимум) нам заведомо не нужны. Поэтому естественно стремление найти способ перехода от данной вершины к лучшей, от нее – к еще лучшей и т.д. Такой способ должен быть дополнен еще, очевидно каким-то признаком того, что лучших чем найденная вершин вообще нет, и признаком того, что данная задача вообще не имеет оптимального решения. В этом и заключается суть симплексного метода поиска решения задачи линейного программирования:
- тем или иным способом находится какая-нибудь вершина многогранника допустимых решений и по определенному правилу проверяется, не является ли она оптимальной. Если она оптимальна – задача решена.
А) Если нет, то по определенному правилу проверяется, нельзя ли утверждать, что задача не имеет оптимального решения (целевая функция не достигает наибольшего значения из-за неограниченности многограннике допустимых решений в направлении роста целевой функции). Если утверждать это можно, то задача неразрешима.
Б) Если нельзя, то по определенному правилу отыскивается новая соседняя, лучшая вершина и осуществляется возврат к 1, в качестве рассматриваемой принимается эта новая вершина.
Гарантируется, что описанный процесс через конечное число переходов к новым вершинам закончится либо на 1, либо на 2. Такой перебор позволяет сократить число шагов при отыскании оптимума. Поясним это на графическом примере.
Пусть область допустимых решений изображается многоугольником ABCDEGH (рисунок) [8]. Предположим, что его угловая точка А соответствует исходному допустимому базисному решению.
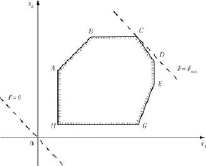
Геометрическая иллюстрация симплексного метода
При беспорядочном переборе пришлось бы испытать семь допустимых базисных решений, соответствующих семи угловым точкам многоугольника. Однако из чертежа видно, что после вершины А выгодно перейти к соседней вершине В, а затем к оптимальной точке С.
Вместо семи перебрали только три вершины, последовательно улучшая линейную функцию. Идея последовательного улучшения решения легла в основу универсального метода решения задач линейного программирования – симплексного метода [3].
Поскольку получение решения задачи линейного программирования сводится к рациональному перебору вершин многогранника допустимых решений, то возникают вопросы: как найти начальную вершину и как перейти к другой вершине? Если использовать алгебраический язык, то последние вопросы можно сформулировать следующим образом: как нейти начальное допустимое базисное решение и как перейти к другому допустимому базисному решению, если начальное оказалось неоптимальным? В соответствии с симплексным методом, чтобы найти какое-нибудь допустимое базисное решение, необходимо разрешить уравнений (4) относительно каких-нибудь m базисных переменных, выразив их через остальные k = n – m свободные переменные. Пусть, например, в качестве свободных выбраны первые k = n – m переменных x1, x2, … xk, а остальные m выражены через них (5):
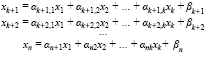
Поскольку переменные x1, …, xk свободные, то им можно придать любые неотрицательные значения. Если свободные переменные приравнять нулю x1 = x2 = … = xk = 0, тo получим базисное решение (0, … 0, βk+1, …, βn)T, которое будет допустимым, если базисные переменные xk+1 = βk+1, xk+2 = βk+2, … xn = βn, в нем неотрицательны. Последнее имеет место в случае, когда все свободные члены βk+1, …, βn неотрицательны. Если и некоторые из базисных переменных окажутся отрицательными, то данный выбор свободных и базисных переменных допустимого решения не дает; соответствующая точка лежит не на границе, а вне многогранника допустимых решений. В последнем случае надо переразрешить систему уравнений относительно каких-то других базисных переменных, но делать это нужно не наугад, а так, чтобы приблизиться к многограннику допустимых решений. После того как найдено допустимое базисное решение, проверяется: не достигнут ли уже максимум целевой функции F. Для этого выражают функцию F через последние поручившиеся свободные переменные, подставив в функцию F вместо базисных переменных xk+1, …, xn их выражения (5) через свободные переменные x1, …, xk. Целевая функция после выполнения такой операции будет представлена с помощью свободных переменных
F = γ0 + γ1x1 + γ2x2 + … + γkxk (6)
Очевидно, что при x1 = x2 = … = xk = 0, F = γ0. Далее выясняется, можно ли улучшить решение, т.е. увеличить функцию F, увеличивая какие-нибудь из переменных x1, x2, …, xk, (уменьшить их нельзя, так как все они равны нулю, а отрицательные значения переменных недопустимы). Если все коэффициенты γ1, γ2, …, γk в выражении (6) отрицательны, то, увеличивая какие-то из переменных x1, x2, …, xk сверх нуля, нельзя увеличить F. Следовательно, найденное решение является оптимальным. Если же среди коэффициентов γ1, γ2, …, γk, в выражении (6) есть положительные, то, увеличивая некоторые из переменных x1, x2, …, xk, а именно те, коэффициенты при которых положительны, можно увеличить F, т.е. улучшить решение. Пусть, например коэффициент γj положителен. Значит есть смысл увеличивать γj, т. е. перейти от данного допустимого решения к другому, где xj > 0. Увеличение xj полезно для целевой функции F, делает ее значения большими. Однако увеличивать xj надо осторожно, так чтобы не стали отрицательными другие переменные xk+1, x k+2, …, xn , выраженные через свободные переменные.
Выясним, когда для базисных переменных xk+1, xk+2, …, xn , опасно увеличение свободных переменных, т. е. когда оно может сделать хотя бы отдельные из базисных переменных отрицательными. Последнее будет иметь место, если, например, коэффициент при xj в каком-то из уравнений (5) отрицателен. Если среди уравнений (5) нет уравнения с отрицательным коэффициентом при xj, то переменную xj можно увеличивать беспредельно, а, значит, линейная целевая функция F не ограничена сверху и оптимального решения не существует. Допустим, что это не так и что среди уравнений (5) есть такие, в которых коэффициент при xj отрицателен, для переменных, стоящих в левых частях этих уравнений, увеличение xj опасно – оно может сделать их отрицательными. Возьмем одну из таких базисных переменных xj и посмотрим, до какой степени можно все же увеличивать, пока переменная xl не станет отрицательной? Выделим из системы (5) l-е уравнение:
xl = αl1x1 + αl2x2 + … + αljxj + … + αlkxk + βl
Здесь свободный член βl ≥ 0, а коэффициент αlj отрицателен.
Если оставить x1 = … = xj–1 = xj+1 = … = xk = 0, то xj можно увеличивать только до значения, равного βl / δlj (получаемого из уравнения αljxj + βl = 0), а при дальнейшем увеличений xj переменная xl станет отрицательной, чего допускать нельзя. Выберем ту из базисных переменных xk+1, xk+2, …, xn , которaя раньше всех обратится в нуль при увеличении xj. Полагая в (5) и (6) все свободные переданные, кроме xj равными нулю, получим
xk+1 = αk+1,j xj + βk+1
…
xn = αnjxj + βn
F = γ0 + γjxj,(γj > 0).
Среди тех базисных переменных xk+1, …, xn в выражения для которых свободная переменная xj входит с отрицательным коэффициентом, найдется, по крайней мэре, одна базисная переменная xr, которая при увеличения xj станет отрицательной раньше других. Для того чтобы определить xr надо найти среди всех отношений –βr/δlj наименьшее, т.е. –βr/δrj = min (βl/δlj), где берутся все l, для которых αlj < 0. Обозначим это минимальное значение δ. Очевидно, что δ > 0. Если минимум достигается сразу при нескольких l, то за r можно брать любое из этих значений l. Теперь xj можно увеличивать до величины δ, не опасаясь, что какая-нибудь базисная переменная станет отрицательной. Положим x1 = 0,…, xj–1 = 0, xj = δ, xj+1 = 0,…, xk = 0 и найдем значения остальных переменных
xk+1 = αk+1,j δ + βk+1
…
xr = αrjδ + βr = 0
…
xn = αnjδ + βn
и целевой функции
F1 = γ0 + γjδ > F,(γj > 0)
В результате проведенных преобразований будет получен новый базис xk+1, …, xr–1, xj, xr+1, … , xn , в котором переменная xr заменена xj (xj = δ) и при этом значение функции F увеличится, т.е. оно приблизится к искомому максимуму целевой функции. Указанные преобразования эквивалентны переразрешению системы уравнений (4) относительно других базисных переменных, при котором переменная xj выводится из числа свободных переданных и вместо нее в группу свободных переменных переводится xr При таких преобразованиях осуществляется переход от базисного решения, в котором x1 = x2 = xj = … = xk = 0, к решению, в котором уже xj ≠ 0, а x1 = … = xj–1 = xr = xj+1 = … = xk = 0.
Предположим, что уравнения типа (5) для нового набора базисных и свободных переменных составлены. Тогда можно выразить через новые свободные переменные и линейную целевую функцию F. Если все коэффициенты при переменных в новом выражении для F отрицательны, то оптимальное решение найдено: оно подучится, если все свободные переменные положить равными нулю. Если среди коэффициентов при переменных целевой функции есть положительные, то процедура улучшения решения продолжается: система ограничений – равенств вновь переразрешается относительно других базисных переменных, и так далее, пока не будет найдено оптимальное решение, обращающее функцию F в максимум.
Приведенное выше описание основной идеи симплексного метода было дано для случая нахождения максимума целевой функции F. Небольшое изменение характера действий позволяет распространить это описание также на случай отыскания минимума функции F. Рассматривая сущность симплексного метода, мы исходили из того, что система уравнений (7) приведена к виду (5), в котором m базисных, переменных выражены через остальные n – m, свободные переменные. Опишем один из методов выделения исходного базиса, называемый методом искусственного базиса.
Пусть система ограничений задана в виде (7), где все bi > 0 (i = I … m). Введем вспомогательные или так называемые искусственные переменные y1,y2, … ym, связанные с x1,x2, … xn уравнениями
y1 = b1 – (α11x1 + … + α1nxn),
……………………… (7)
ym = bm – (αm1x1 + … + αmnxn)
Очевидно, что система (7) имеет то же самое решение, что и система (4), при условии y1 = y2 = … = ym = 0. В системе (4) искусственные переменные y1,y2, … ym образуют базисные переменные. Используя эти переменные, можно перейти к совокупности других m базисных переменных, не содержащей ни одной искусственной переменной, например, к x1,x2, … xm.
Допустим, что после некоторых преобразований система (7) приведена к виду
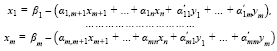(8)
где β1 ≥ 0, …, βm ≥ 0.
В системе (8) мы инеем право положить y1 = y2 = … = ym = 0, тогда эта система становится эквивалентной система (5). В системе (8) переменные x1,x2, … xm являются базисными переменными, т. е. тем самым задача выделения исходного базиса решена.
Оказывается, что для перехода от системы (7) к системе (8) можно применить симплексный метод. Действительно, будем при помощи этого метода решать задачу о минимизации функции
f = y1 + y2 + … + ym
при ограничениях, заданных системой (7), и условиях не отрицательности переменных x1 ≥ 0, …, xn ≥ 0, …, ym ≥ 0. Система (7) записана в таком виде (выделен базис y1, … ym ), что может быть непосредственно применен симплексный метод. После некоторого числа шагов искомый минимум, очевидно, будет получен, причем, так как f ≥ 0, то и min f ≥ 0.
Очевидно, если min f > 0, система (8) не может иметь неотрицательных решений, для которых все y1 = 0, …, ym = 0. Следовательно, и исходная система (7) также не может иметь неотрицательных решений, т. е. эта система не удовлетворяет условиям, которым должна удовлетворять система ограничений задачи линейного программирования, и эта задача в данном случае не имеет радения (система (7) несовместна).
Если min f = 0, то вследствие не отрицательности y1,y2, … ym должны быть равны нулю все искусственные переменные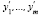 
входящие в базисное решение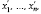 
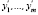, которое минимизирует функцию f. Это означает, что в случае min f = 0 данная система ограничений (7) совместна. Далее необходимо убедиться в том, что искусственные переменные не входят в базис. В противном случае следует проделать дальнейшие преобразования, чтобы вывести их из базиса.
Таким образом, мы показали, как выделить первый исходный базис для любой совместной системы ограничений, используемых в задачах линейного программирования. Укажем теперь некоторые формальные правила, облегчавшие вычисления по алгоритму симплексного метода.
Процесс получения решения задачи линейного программирования симплексным методом является шаговым. Поэтому оказывается удобным записывать результаты каждого вида в виде так называемых симплексных таблиц, заполняемых по определенным правилам. Каждое тождественное преобразование системы ограничений-равенств сводится к переходу от одной формулы к другой. Для простоты предположим, что нам известно первое допустимое базисное решение, т. е., систему ограничений-равенств задачи (4) можно записать в виде
x1 = β1 – (α1,m+1xm+1 + α1,m+2xm+2 + … + α1,nxn),
………………………………………… (9)
xm = βm – (αm,m+1xm+1 + αm,m+2xm+2 + … + αm,nxn)
где все βi ≥ 0.
Это предположение нисколько не снижает общности, изложения, только делает его короче. Целевую функцию будем записывать как в виде,
F1 = c1x1 + c2x2 + … + cnxn,
так, и в виде
F1 = λ0 + (λm+1xm+1 + … + λnxn),
получаемом после подстановки вместо базисных переменных их выражений через свободные переменные, где F1 – значение функции F, соответствующее первой симплексной таблице.
Составим первую симплексную таблицу (таблица).
Симплексная таблица
|
Базис |
Коэффициенты целевой функции |
Свободные члены |
c1 |
c2 |
…… |
cm+1 |
…… |
cn |
|
x1 |
x2 |
…… |
xm+1 |
…… |
xn |
|||
|
x1 |
c1 |
β1 |
I |
0 |
…… |
α1m+1 |
…… |
α1n |
|
x2 |
c2 |
β2 |
0 |
I |
…… |
α2m+1 |
…… |
α2n |
|
….. |
……. |
…. |
…. |
….. |
…… |
……. |
…… |
…… |
|
xm |
cm |
βm |
0 |
0 |
…… |
αm,m+1 |
…… |
αmn |
|
Целевая функция |
F1 |
λ0 |
0 |
0 |
……. |
λm,m+1 |
……. |
λn |
В данную таблицу записываются в определенном порядка все величины, которые требуются в процессе получения решения задачи. Последнюю строку этой таблицы принято называть индексной строкой.
В том случае, когда все элементы индексной строки (кроме λ0) таблицы при решении задачи на максимум положительны (или при решении задачи на минимум – отрицательны), то полученное решение является оптимальным. Этим решением будет x1 = β1, x2 = β2, xm = βm, xm+1 = 0, xm+2 = 0, ... xn = 0. Значение целевой функции при этом, очевидно, равно
F1 = c1β1 + c2β2 + … + cmβm, (F1 = λ0).
Если же среди элементов индексной строки есть отрицательные при решении задачи на максимум (положительные при решении задачи на минимум), то полученное решение не является оптимальным. В этом случае выбираем соответствующий наибольший по абсолютной величине элемент индексной строки. Изменение свободной переменной, входящей с выбранным коэффициентом в выражение для целевой функции, будет в наибольшей степени увеличивать значение целевой функции по сравнению с изменением любой другой свободной переменной (в наибольшей степени уменьшать значение целевой функции – в задаче на минимум). Выбранный элемент определяет ведущий столбец таблицы (например, столбец с номером C).
Далее необходимо выделить ту базисную переменную, которая станет отрицательной раньше других базисных переменных при увеличении свободной переменной ведущего столбца (переменной xs). Для этого составляют отношения свободных членов (третий столбец) к положительным элементам C-го (ведущего) столбца и выбирают из них наименьшее. Пусть этим наименьшим отношением будет βr/αrs, т.е.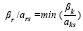 
(все αks > 0). Тогда r-я строка называется ведущей строкой. На пересечении r-й строки и C-го столбца находится элемент αrs, который называется разрешающим элементом.
Следующим этапом является переход к новому базису, в котором переменная xr из базисных переводится в небазисные, а переменная xs делается базисной. Этот переход означает переход ко второй симплексной таблице. Получим формулы, с помощью которых следует вычислять элементы новой таблицы.
Переход к новой таблице осуществляется с помощью следующих тождественных преобразований, а именно r-е уравнение системы (9) следует разрешить относительно переменной xs:
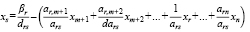
Это выражение для xs представляется во все остальные уравнения и в выражение для функции F. Например, подстановка значения xs в k-e уравнение (k ≠ S) системы (9) приводит к уравнению:
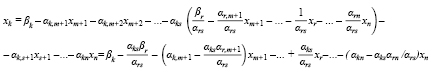
Аналогично подстановка значения xs в целевою функцию F приводит к выражению
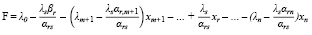
Таким обрезом, из выражения для xs следует, что элементы r-й строки новой таблицы равны соответствующим элементам отарой таблицы, разделенным на разрешающий элемент
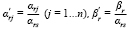(10)
Элементы C-го столбца новой таблицы все равны 0, за исключением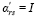 
, так как стала базисной переменной и больше не входит в правую часть системы уравнений. Чтобы получить любой другой элемент новой симплексной таблицы, нужно от соответствующего элемента прежней таблицы отнять произведение элемента ведущей строки на элемент ведущего столбца, разделанное на разрешающий элемент, т. е.
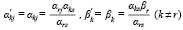(11)
Коэффициенты функции F или все элементы индексной строки новой симплексной таблицы могут быть вычислены по формулам:
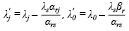(12)
Вторая симплексная таблица имеет такой же вид, кая и первая симплексная таблица. Только теперь переменная xs стала базисно переменной и коэффициенты βi, λij, λj заменяются на β'i, λ'ij, λ'j .
Если сразу все коэффициенты в индексной строке для свободных переменных оказались положительными (в задаче на максимум) или отрицательными в задаче на минимум), то оптимальное решение получено, и целевая функция принимает значение
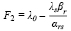
где F1 – значение целевой функции во второй симплексной таблице. Соответственно, если эти условия не выполняются, необходимо переходить к следующей симплексной таблице, проводя тождественные преобразования по установленным выше правилам. Укажем дополнительно ещё одну возможность вычисления элементов индексной строки, исходя из представления целевой функции в виде F1 = c1x1 + c2x2 + … + cnxn. Для этого преобразуем данное выражение следующим образом:
F1 = c1x1 + … + cnxn = = c1 (β1 – α1,m+1xm+1 – α1,m+2xm+2 – … – α1nxn) + c2 (β2 – α2,m+1xm+1 – α2,m+2xm+2 – … – α2nxn) +
+ cm (βm – αm,m+1xm+1 – αm,m+2xm+2 – … – αmnxn) + cm+1xm+1 + cm+2xm+2 + … + cnxn
Объединив свободные члены и коэффициенты при xm+1, xm+2, …, xn, получим
F1 = c1β1 + c2β2 +… + cmβm + (cm+1 – c1α1,m+1 – c2α2,m+1 – … – cmαm,m+1) xm+1 + … + (cn – c1α1n – c2α2n – … – cmαmn) xn
Таким образом, мы получили явное выражение для коэффициентов целевой функции через коэффициенты αij, βi, и ci
λ0 = c1β1 + c2β2 +… + cmβm,
λj = c1β1j + c2β2j +… + cmβmj – cj,
где j = m + 1, m + 2, … , n.
Обозначим c1β1j + c2β2j +… + cmβmj через hj . Тогда λj = hj – cj и элементы индексной строки могут вычисляться па этой формуле после того, как получены все элементы λij, i = 1 … m. При этих вычислениях используются элементы c1,c2, … cn, повторяющиеся в каждой симплексной таблице.
Итак, после конечного числа шагов будет либо получено оптимальное решение или установлено, что задача не имеет решения. При этом, однако, иногда могут встретиться случаи вырождения и зацикливания.
Скучай вырождения встретится, если свободный член уравнения, содержащего разрешающий элемент, равен нулю. В этом случае после очередного шага значение целевой функции не увеличится (или не уменьшится).
Поскольку значения базисных переменных ранения, равны свободным членам соответствующих уравнений (небазисные переменные мы принимаем разными нулю), то случай вырождения равносилен тему, что одна юга несколько базисных переменных равны нулю. В этом случае (l + I)-e значение целевой функции совпадает с l-м значением, т. е. Fl+1 = Fl. Ясно, что это произойдет в том случае, если в последовательности базисов некоторые из них будут повторяться. При этом может случиться, что на каждом из последующих шагов имеет место вырождение, т. е. Fl = Fl+1 = Fl+2 = … . В этом случае говорят, что в процессе решения задачи произошло зацикливание. Отметим, однако, что при решении конкретных задач случаи зацикливания крайне редки, причем его всегда мощно набежать, если изменить последовательность выбора базисов.
Указанная выше последовательность операций определяет алгоритм симплексного метода. Этот алгоритм позволяет решать задачи линейного программирования на программном продукте.
Комплексный анализ охватывает всю совокупность факторов и показателей явления (процесса). Учитывая его значимость, он будет рассмотрен отдельно.
В свою очередь тематический военно-экономический анализ связан с необходимостью анализа одного из факторов и показателей явления.
Классификация военно-экономического анализа по степени охвата анализируемых объектов предусматривает разделение на военно-хозяйственный и межхозяйственный военно-экономический анализ. При этом в первом случае, анализу подвергается отдельно взятая военно-хозяйственная единица, а во втором анализ осуществляется способом сравнения результатов (факторов и их показателей) военно-экономической деятельности однотипных (сопоставимых) военно-хозяйственных единиц.
Кроме того, следует дополнить данную классификацию в связи с переходом Вооруженных сил РФ на бюджетный учет с 1.01.2005 года, поскольку это позволяет применять практически в полном объеме управленческий учет и его методы, в том числе контроллинг, даже в воинской части.
Таким образом, разработка эффективной системы комплексного военно-экономического анализа ресурсного обеспечения Вооруженных сил является важнейшим условием реализации системного комплексного подхода. Системный анализ экономики Вооруженных сил заключается в том, что она (экономика) рассматривается в качестве относительно обособленной системы в рамках экономической системы более высокого порядка.
Этап выбора решений связан с проведением комплекса расчетов, в котором активную роль играют эксперты, используются математические методы, расчетные алгоритмы и вычислительная техника. Роль симплексного анализа на данном этапе заключается в определении стратегии и критериев выбора, а также в анализе зависимости результатов выбора от важности показателей оценивания и применяемых критериев, системы предпочтений и других исходных данных. Эффективное проведение этого анализа требует оперативного выполнения расчетов, что может быть реализовано с помощью диалогового режима общения на программном продукте рассчитать расходы в плановом режиме. В связи с этим возникают две конкретные задачи автоматизации выбора решений; разработка комплекса программ для реализации в программном продукте расчетных алгоритмов задачи выбора, а также разработка сервисных программ для обеспечения диалогового режима работы, ввода и вывода информации.
Выполнение этих задач осуществляется автоматизированной подсистемой выбора решений, являющейся составной частью автоматизированной системы анализа и прогнозирования расчетов по расходам не только финансовым, но и любым затратам на оборону государства.
Таким образом автоматизированная система анализа и прогнозирования характеристик должна включать следующие основные элементы:
- объект исследования, представленный набором имитационных и прогнозных моделей различных уровней детализации его описания и моделей входных воздействий для них. Использование набора моделей различной степени сложности позволяет расширить круг задач, решаемых с помощью автоматизированной системы на разных стадиях движения затрат, а также увеличить объем и повысить качество распределения расходов по отраслям, необходимой для экономического сопровождения системы;
- банк, обеспечивающий прием, хранение и выдачу средств, необходимых для решения возникающих проблем в связи с боевой подготовкой;
- библиотеку модулей процедур анализа, подготовки и принятия решений, например, таких, как процедуры анализа чувствительности показателей назначения к воздействующим факторам, оптимизации, выделения множества эффективных решений и т.п.;
- управляющую программу, которая в соответствие с поставленной задачей исследований осуществляет выбор необходимых процедур и исходных данных, организует проведение имитационных экспериментов и выполнение формализованных, процедур анализа, а также осуществляет выдачу результатов исследования на внешние устройства.