Введение
Решение проблемы идентификации сигналов, свидетельствующих о росте волатильности капитала, обращающегося на рынке вкладов населения и привлекаемого кредитными организациями, является частью комплексной задачи функциональной диагностики финансовой системы в целом. Ранее в работе [1] для этой цели была предложена система показателей, позволяющих проводить анализ поведения кредитных организаций в отношении управления сбалансированностью базовых финансовых фондов (а именно в части управления ликвидной позицией). Применение предложенной в работе [1] совокупности показателей для решения проблемы идентификации и мониторинга риска волатильности капитала, привлекаемого системой кредитных организаций РФ, позволяет качественно решить поставленную проблему только в том случае, если рассматриваемую систему считать единым и неделимым целым. Однако система кредитных организаций является сложным, неоднородным, структурированным объектом. Пример структурирования подобной системы также был приведен в работе [1], он предполагал группировку кредитных организаций в виде четырех кластеров по величине чистых активов (крупнейшие, крупные, средние, малые). Общесистемный количественный показатель из-за значительной концентрации ресурсов в крупнейших кредитных организациях (далее – кластер «Крупнейшие») фактически близко повторяет значения индикатора кластера «Крупнейшие» и слабо иллюстрирует поведение остальных кластеров. Для точной идентификации риска волатильности, который может возникнуть из-за разбалансированности финансовой системы в результате миграции клиентуры и капитала из кредитных организаций других клаcтеров, потребуется расчет показателя для каждого кластера, последующий анализ динамики данных индикаторов, изучение согласованности или рассогласованности политики по управлению ликвидной позицией того или иного кластера кредитных организаций. Подобный подход действий частично решает проблему, но представляется трудоемкой задачей. Поэтому возникает необходимость модернизации методов, применяемых при решении мониторинговой задачи по оценке и идентификации риска волатильности капитала, обращающегося на рынке вкладов населения и привлекаемого кредитными организациями. При этом предлагаемый метод должен учитывать особенности структурирования системы кредитных организаций и должен позволять оценить уровень согласованности политики управления ликвидной позицией разных кластеров системы при формировании финансовых резервов для покрытия возможного оттока средств с банковских вкладов частных лиц.
В рамках современного системного подхода и общей теории систем информация рассматривается в качестве количественной меры тесноты и согласованности взаимодействия системных элементов. Именно поэтому информацию можно считать количественной мерой системной стабилизации, либо дестабилизации. Формализацию информационного показателя при решении поставленной диагностической задачи планируется осуществить в рамках энтропийного моделирования.
В процессе анализа исследований, посвященных применению энтропийного подхода для оценки состояния банковского сектора, были изучены следующие работы. Мерви Тойванен, используя метод максимума энтропии, оценивает опасность развития масштабного банковского кризиса в Финляндии в 2005-2007 годах через рынок финского межбанковского капитала [2]. В своем анализе процесса распространения кризиса автор учел опыт Финского банковского кризиса 1990-х. В работе Джианпинг Ли и др. [3] на основе данных фондового рынка авторами формируется энтропийная модель, определяется степень взаимосвязанности китайских банков и моделируется процесс реализации системных рисков в банковском секторе Китая. Моника Биллио и коллеги в своем исследовании [4] формулируют подход к оценке и прогнозированию системного риска банковского сектора на основе расчета энтропийных показателей. В данном исследовании авторы объединяют методику расчета специальных Value-at-Risk-характеристик с энтропийным моделированием. По итогам анализа представленных работ, можно констатировать слабую разработанность изучаемой проблемы и отсутствие достаточно простых и адекватных математических моделей, позволяющих связать энтропию с фактическими характеристиками состояний системы кредитных организаций.
Теоретические аспекты
и методы исследования
В рамках данной статьи сформулируем доступную для понимания экономистов математическую модель, позволяющую связать энтропию с фактическими характеристиками состояний системы кредитных организаций, иллюстрирующими реакцию данного объекта на волатильность капитала на рынке частных вкладов. Сектор кредитных организаций можно считать сложным структурированным системным объектом. Представим его в качестве кредитных организаций, сгруппированных по четырем кластерам. В качестве группировочного критерия будем использовать величину чистых активов. Прорейтингуем кредитные организации по данному критерию по убыванию. Первые 30 кредитных организаций по размеру чистых активов будут объединены в первый кластер, который условно назовем «Крупнейшие». Кредитные организации с 31 по 100 место сформируют второй кластер – «Крупные». В третий – «Средние» войдут кредитные организации с 101 по 200 место. В четвертый кластер, именуемый «Малые», будут включены остальные.
Указанную математическую модель можно условно представить в виде многомерной случайной величины Y=(Y1,Y2,…Ym). При этом следует допустить, что каждая составляющая Yi вектора Y является одномерной случайной величиной. В рамках нашей модели она будет характеризовать процесс того, как тем или иным кластером осуществляется управление соотношением между объемом привлеченных средств частных клиентов и величиной высоколиквидных активов, способных покрыть отток клиентского капитала. В дальнейшем под таким управлением мы будем понимать реализацию политики управления ликвидной позицией соответствующего кластера. Состояние сектора кредитных организаций с учетом кластеризации в предыдущий и текущий период времени можно будет описать через две системы непрерывных случайных величин
Y(1) = (Y1(1), Y2(1),…, Ym(1))
и Y(2) = (Y1(2), Y1(2),…, Ym(2)).
Составляющие указанных систем непрерывных случайных величин Yi(1), Yi(2) (i=1,2,...,m), будут иметь конечные дисперсии и будут характеризоваться однотипными распределениями с некоторыми параметрами положения и масштаба. Факторы модели могут быть как коррелируемыми, так и независимыми. Тырсин в своей работе [5], развив положения, предложенные Шенноном [6], обосновывает возможность применения энтропийного подхода при разработке диагностической модели стохастической системы. Основываясь на подходе энтропийного моделирования, предложенного Тырсиным А.Н. и Лебедевой-Ворфоломеевой О.В., изменение состояния моделируемого объекта определим через энтропийный критерий, представляющий собой сумму энтропийных элементов. В случае, когда вектор Y является гауссовским, энтропийный критерий вычисляется по формуле:
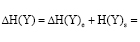
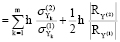(1),
где
–
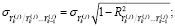
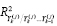индексы детерминации соответствующих регрессионных зависимостей
(k= 2,3,…,m; j=1,2);
ΔH(Y)e – положительный или отрицательный прирост энтропии за счет изменения дисперсий случайных величин Y1,Y2,…Ym при переходе системы из предыдущего состояния (состояние 1) в текущее состояние (состояние 2);
ΔH(Y)s – положительный или отрицательный прирост энтропии за счет изменения корреляций случайных величин Y1,Y2,…Ym при переходе системы из предыдущего состояния (состояние 1) в текущее состояние (состояние 2);
где |RY(j)| – определитель корреляционной матрицы R Y(j) случайного нормально распределенного вектора Y(j) , j=1,2 [7].
Первое слагаемое ΔH(Y)e определяет положительный или отрицательный прирост энтропии за счет изменения частоты пересмотра (изменчивости) типа текущей политики каждого кластера кредитных организаций по управлению ликвидной позицией с учетом ситуации на рынке вкладов. Второе слагаемое ΔH(Y)s отражает положительный или отрицательный прирост энтропии за счет изменения степени взаимосвязанности политик управления рисками волатильности кластеров системы кредитных организаций. Примеры идентификации ситуаций с помощью энтропийного критерия и его элементов представлены в таблице 1.
Таблица 1
Диагностическая карта возможных ситуаций на рынке вкладов населения
в зависимости от значений элементов энтропийного критерия
|
Элемент |
ΔH(Y)e > 0 |
ΔH(Y)e < 0 |
|
ΔH(Y)s > 0 |
Условия 1. Частота пересмотра применяемого тем или иным кластером типа политики возрастает. 2. Взаимосвязанность политик, применяемых кластерами, сокращается. Вариант ситуации Дестабилизация системы в результате кризиса при этом кластеры не перетягивают клиентский капитал друг у друга. Вывод Уровень волатильности капитала повышается в рамках анализируемого периода. |
Условия 1. Частота пересмотра применяемого тем или иным кластером типа политики снижается. 2. Взаимосвязанность политик, применяемых кластерами, сокращается. Вариант ситуации 1.Система кредитных организаций не успевает за ростом емкости рынка (притоком капитала), конкуренция снижается. 2. Кредитные организации, ослабленные кризисом, не обладают ресурсами для активного управления ликвидной позицией. 3. Уровень конкурентной борьбы – низкий. 3. Централизованная финансовая помощь кредитным организациям (от государства или ЦБ) в условиях кризиса (она защищает от волатильности ресурсной базы и снижает зависимость политики кластеров по управлению ликвидной позицией от ситуации на рынке вкладов). Вывод Уровень волатильности капитала характеризуется изменением общего энтропийного критерия. |
|
ΔH(Y)s <0 |
Условия 1. Частота пересмотра применяемого тем или иным кластером типа политики возрастает. 2. Взаимосвязанность политик, применяемых кластерами, повышается. Варианты ситуации 1. Отток (или приток) капитала, затронувший все кластеры. 2. Интенсивное вытеснение с рынка одних кластеров другими. 3. Реализация варианта 1 и 2 одновременно. 4. Начало организованного раздела рынка клиентского капитала между кластерами (может быть инициирован ЦБ, правительством, банковским сообществом). Вывод Уровень волатильности капитала характеризуется изменением общего энтропийного критерия |
Условия 1. Частота пересмотра применяемой тем или иным кластером политики снижается. 2. Взаимосвязанность политик, применяемых кластерами, повышается. Варианты ситуации 1. Постепенное вытеснение с рынка одних кластеров другими. 2. Ситуация, когда рынки клиентского капитала поделены между кластерами. Вывод Уровень волатильности капитала снижается в рамках анализируемого периода. |
В качестве показателя, позволяющего определить риски волатильности капитала, введем параметр, характеризующий политику управления ликвидной позицией (ответную реакцию на возможную волатильность) соответствующего кластера системы кредитных организаций. Данный показатель был предложен в работе [1]. Он рассчитывается как коэффициент отношения высоколиквидных активов к объему вкладов физических лиц (IDV (см. формулу 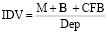2)).
(2),
где M – денежные средства кредитных организаций (всех или соответствующих определенному кластеру), учитываемые по активному счету первого порядка 202 на начало каждого месячного периода, включающие наличную валюту и чеки (в том числе дорожные чеки), номинальная стоимость которых указана в иностранной валюте [1].
IB – средства кредитных организаций (всех или соответствующих определенному кластеру) на корреспондентских счетах в кредитных организациях – корреспондентах, учитываемые по активным счетам второго порядка 30110 и 30118, на начало каждого месячного периода [1].
CFB – средства кредитных организаций (всех или соответствующих определенному кластеру) на счетах в Банке России и в уполномоченных органах (иностранных банковских регуляторах) других стран, учитываемые по активному счету первого порядка 319 и активным счетам второго порядка 30102, 30104, 30106, 30125, 30202, 30204, 30208, 30210, 30211, 30213, 30224, 30228, 30238, 30235, 30417, 30419, 32902, на начало каждого месячного периода [1].
Dep – средства физических лиц, привлеченные кредитными организациями (всеми или соответствующими определенному кластеру), отражаемые на пассивных счетах первого порядка 423, 426, 522 и пассивных счетах второго порядка 40803, 40813, 40817, 40820, 40823, 40824, 40826, 47603, 47605, 52404 на начало каждого месячного периода [1].
Информационной базой для построения динамических рядов показателя IDV для четырех кластеров системы кредитных организаций, послужили данные сайта analizbankov.ru [8]. Периодом анализа выступает временной интервал с 01.01.2014 по 01.01.2020.
На основе динамических рядов месячных значений показателя IDV для четырех кластеров системы кредитных организаций была сформирована матрица исходных данных. Для повышения точности модели был укрупнен временной период, описывающий стационарное состояние системы кредитных организаций с месячного до двухгодового. Энтропийное моделирование проведем на базе полученной системы факторов Y1=IDV 1 (кластер «Крупнейшие»), Y2=IDV 2 (кластер «Крупные»), Y3=IDV 3 (кластер «Средние»), Y4=IDV4 (кластер «Малые») в виде вектора
Y = (Y1,Y2,Y3,Y4). Каждый вектор соответствует двухгодичному периоду. Период 1 включает интервал значений факторов за 2014-2015 годы, период 2 – интервал значений факторов за 2016-2017 годы, период 3 – интервал значений факторов за 2018-2019 годы. Проверка по критерию Колмогорова-Смирнова подтвердила выполнение для векторов Y закона нормального распределения. С помощью пакета SPSS Statistics 17.0 были рассчитаны для каждого вектора корреляционные матрицы факторов и дисперсии факторов. Далее был вычислен определитель каждой корреляционной матрицы. Полученные результаты представлены ниже:
;
;
;
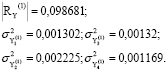
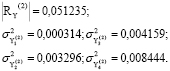
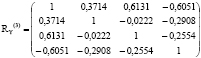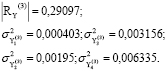
Вычислим изменение энтропии системы для каждого периода по формуле 1.
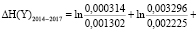
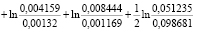= 1,04823+(-0,32773)= 0,720495.
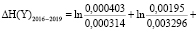
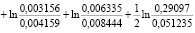= -0,41992 + 0,868396= 0,448478.
Результаты исследования
и их обсуждение
Динамика значений энтропийного критерия рынка вкладов РФ, иллюстрирующего уровень волатильности капитала для двухгодовых временных интервалов с 2014 года по 2019 год представлена в таблице 2.
Таблица 2
Результаты оценки
энтропийного критерия, иллюстрирующего уровень волатильности на рынке вкладов
|
Периоды |
1-2 |
2-3 |
|
H(Y)e |
1,04823 |
-0,41992 |
|
H(Y)s |
-0,32773 |
0,868396 |
|
H(Y) |
0,720495 |
0,448478 |
В 2014-2015 годах кредитные организации РФ столкнулись с финансовым кризисом, порожденным международными санкциями и падением цен на нефть. Анализ изменения энтропийного критерия и его элементов в посткризисный двухлетний период (2016-2017 гг.) свидетельствует о росте энтропии (на 0,720495 условных единиц). Данное изменение достигается за счет роста энтропийного элемента H(Y)s на 1,04823 условные единицы, подтверждающего усиление взаимосвязанности политик по управлению ликвидной позицией для всех кластеров, а также за счет сокращения величины энтропийного элемента H(Y)e на 0,32773 условные единицы, что говорит о повышении частоты пересмотра применяемых тем или иным кластером типов политик. Увеличение энтропийного показателя может свидетельствовать об эндогенных и экзогенных процессах, протекающих в системе кредитных организаций РФ. Эндогенные процессы связаны с перетоком капитала от одних кластеров в другие. Экзогенные процессы проявляются в оттоке капитала из финансовой системы. В последующий двухлетний период (2018-2019 гг.) энтропия возросла на 0,448478 условных единиц. Изменение энтропийного элемента H(Y)e на -0,41992 условные единицы говорит о снижение частоты пересмотра типов политик, реализуемых кластерами, что косвенно свидетельствует о частичной стабилизации сектора кредитных организаций. Тем не менее, рост показателя H(Y)s на 0,868396 условных единиц позволяет сделать вывод о том, что несогласованность действий кредитных организаций при управлении ликвидной позицией возросла. С учетом примеров диагностической таблицы 1, можно сделать вывод о снижении конкуренции на рынке вкладов РФ.
Выводы
В рамках настоящей статьи была решена частная задача функциональной диагностики по идентификации сигналов, свидетельствующих о росте волатильности капитала, обращающегося на рынке вкладов населения и привлекаемого кредитными организациями. В ходе решения задачи была сформулирована диагностическая энтропийная модель, учитывающая сегментацию системы кредитных организаций РФ на четыре кластера. Входными данными модели послужили значения показателя, характеризующего политику управления ликвидной позицией (формализованную ответную реакцию на возможную волатильность) соответствующего кластера системы кредитных организаций. Выходными данными модели выступили значения энтропийного показателя, описывающего изменение уровня волатильности капитала, а также значения его составных элементов. Анализ полученных с помощью модели данных позволил сделать вывод о росте волатильности базовых финансовых фондов кредитных организаций и, как следствие, о росте волатильности на рынке вкладов населения с 2014 по 2019 годы.
Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 18-010-00909.