Экономическое развитие любой страны невозможно без постоянного качественного пополнения трудовых ресурсов, которое можно обеспечить только в условиях устойчивого демографического прироста населения. Однако из-за мировых тенденций по снижению уровня рождаемости все чаще приходится констатировать отсутствие даже простого воспроизводства, которое характеризуется тем, что коэффициент депопуляции, представляющий собой отношение показателя рождаемости к показателю смертности за определенной период, имеет значение меньше 1.
Резкое нарушение воспроизводства населения России относится к началу 1990-х годов. На протяжении всего XX века в России было несколько демографических кризисов, вызванных первой мировой (1914-1918) и гражданской (1917-1922) войнами, массовым голодом в начале 30-х годов, Великой Отечественной войной (1941-1945), которые унесли жизни огромного количества трудоспособного, по большей части мужского населения [1]. Численность населения после этих событий в стране удалось восстановить, однако рождаемость после указанных событий стала снижаться. Обвальное снижение рождаемости и значительный рост смертности начались с 1989 года и стали следствием разрушения идеологических принципов и ценностей общества, утраты традиционных устоев крепкой семьи, потери мужчиной роли главы семьи и кормильца, отдаления женщины от семьи, ухудшения качества медицинского обслуживания населения. Тяжелейшие экономические и социальные потрясения привели к снижению доходов населения, сокращению рабочих мест по всей стране, жилищным проблемам и т.п., что в итоге привело к резкому увеличению разводов и вызвало рост смертности как среди взрослых, так и молодежи, по причине самоубийств, заболеваниям наркоманией и алкоголизмом. В этом свою отрицательную роль сыграла западная пропаганда раннего сексуального воспитания, свободы выбора пола, однополых браков.
Все это в совокупности привело к тому, что Россия по рождаемости опустилась до уровня развитых стран, при этом индексы интенсивности смертности поднялись до уровня развивающихся стран. Только за период с 1990 по 2010 год население страны уменьшилось на 5 млн. человек [2]. Не смотря на принятый закон о выплате «материнского капитала» на второго и последующего ребенка [3], концепцию о демографической политике на период до 2025 года [4], общая численность населения по данным Росстата на 2015 год составила 146,3 млн и достигла уровня 2001 года только за счет учета проживающих в Республике Крым и городе Севастополь, вошедших в состав РФ [5]. Государственная поддержка института семьи и стимулирование деторождения [6] несколько улучшило ситуацию по восстановлению популяции в стране начиная с 2015 года, во многих регионах впервые за несколько десятилетий рождаемость превысила смертность. Однако, как скоро демографическая ситуация улучшится настолько, чтобы не представлять собой угрозу постепенного вымирания страны, не могут точно сказать даже эксперты.
Целью данного исследования является проведение эконометрического анализа процесса депопуляции населения России для определения возможных тенденций по сокращению/приращению народонаселения России в ближайшие годы.
Материалом для исследования являются статистические данные с 1989 по 2018 годы, имеющиеся в свободном доступе [7]. Используемые методы исследования – статистический анализ временных рядов для построения адекватной модели по прогнозированию будущих значений уровней ряда.
В статье представлены результаты проведенного анализа по выбору структуры временного ряда, исследования свойства его стационарности, определения характера влияния случайных факторов на изучаемую эндогенную переменную и вычисления их количественной меры воздействия. Наилучшим образом описывает изменение количества населения в России смешанная модель авторегрессии и скользящего среднего порядка ARMA(1,2).
Рассмотрим динамику годовых показателей в период 1989-2018 гг. количества населения в миллионах человек – обозначим их как yt (рисунок 1).
Рассматриваемый датированный набор значений yt представляет собой модель временного ряда, в которой каждое значение уровня yt объясняется при помощи фактора времени t. Определим вид данного временного ряда.
Поскольку на графике динамики годовых показателей (Рис. 1) явно прослеживается убывающий тренд, а сезонная (циклическа) компонента в значениях уровней ряда не присутствует, спецификацию модели временного ряда представим в простейшем виде как
yt = α + β•t + ut. (1)
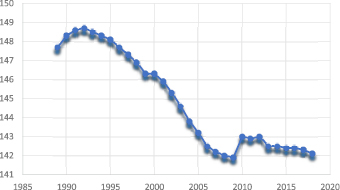
Рис. 1. Динамика годовых показателей количества населения России (в млн. человек)
Проведем оценку параметров модели (1) методом наименьших квадратов (МНК реализован во встроенной функции «ЛИНЕЙН» – здесь и далее все вычисления будут проводиться в Microsoft Excel) и по оцененной модели
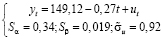(2)
проверим качество предложенной спецификации модели (1) по F-тесту. В ходе теста выдвигается две гипотезы: основная – все коэффициенты уравнения регрессии (1) равны нулю, то есть ни одна из объясняющих переменных не является значимой, альтернативная – хотя бы один коэффициент не равен нулю:
H0:α = β = 0, H1:α ≠ β ≠ 0.
Требуют реализации последующие шаги по проведению F-теста:
1. Найти значение F-статистики для набора данных и определить (1 – α)-квантиль Fкрит = F1 – α распределения Фишера.
2. При справедливости неравенства F ≤ Fкрит принять основную гипотезу или отвергнуть в противоположном случае.
При принятии нулевой гипотезы спецификация модели признается некачественной.
В результате проведения F-теста получили: F = 198,09; Fкрит = 4,196, то есть качество модели (1) признается удовлетворительным. Каждое значение уровня yt объясняется функцией регрессии на уровне 88 %, на что показывает значение коэффициента детерминации модели. Однако, как следует из (2), значение случайного фактора в каждый момент времени t может примерно на 0,92 млн. увеличивать/уменьшать ожидаемое значение численности населения yt, что является весьма существенным отклонением.
В связи с этим проверим статистическую значимость объясняющих переменных модели по критерию Стьюдента (t-тесту). Выдвигается две гипотезы: основная – коэффициент при интересуемой переменной равен нулю, альтернативная – коэффициент при интересуемой переменной не равен нулю:
H0:ai = 0, H1:ai ≠ 0.
Требуется выполнить следующие шаги t-теста:
1. Найти значение дроби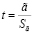 
для каждого коэффициента регрессии и определить двусторонний (1 – α)-квантиль tкрит распределения Стьюдента.
2. При справедливости неравенства t ≤ tкрит принять основную гипотезу или отвергнуть в противоположном случае.
При принятии нулевой гипотезы переменная признается незначащей, она может быть удалена из модели.
Констатируем, что поскольку для модели (2) все значения t – статистик (tα = –14,07, tβ = –435,02 не превышают уровня tкрит = 2,045, то все объясняющие факторы в уравнении регрессии (1) являются значимыми.
Определение приближенных значений коэффициентов модели (1) и их среднеквадратических отклонений проводилось по методу наименьших квадратов (МНК). Но является ли данная процедура для (1) самой оптимальной?
Для выяснения оптимальности метода оценивания параметров модели (1) проверим входящие в нее случайные возмущения на гомоскедастичность (отсутствие зависимости между объясняемыми переменными и случайным остатком) по тесту Голдфелда-Квандта и наличие автокорреляции (зависимости случайных остатков предыдущего периода от текущего) с помощью теста Дарбина-Уотсона [8].
В ходе данного теста Голдфелда-Квандта выдвигается две гипотезы: основная гипотеза – случайное возмущение гомоскедастично, альтернативная – случайное возмущение гетероскедастично:
.
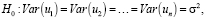
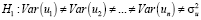Распишем последующие шаги по проведению теста Голдфелда-Квандта:
1. Произведем сортировку всех данных временного ряда по возрастанию значений t.
2. Разделим наши данные на три части: 1 – первые ⌈0,3n⌉ строк (n – количество уравнений наблюдений); 3 – последние ⌈0,3n⌉ строк; 2 – все оставшиеся строки.
3. Оценим коэффициенты методом наименьших квадратов при помощи функции «ЛИНЕЙН» (здесь и далее все вычисления будут проводиться в Microsoft Excel) 1 и 3 части наших данных.
4. Рассчитываем модельную статистику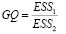 
и определяем проверочную статистику как (1 – α)-квантиль Fкрит = F1 – α распределения Фишера.
5. При выполнении следующих условий остаток признается гомоскедастичным:
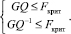
В результате проведения теста получили:
GQ = 1,74; GQ-1 = 0,57; Fкрит = 3,44.
Оба условия теста Голдфелда-Квандта выполняются, что указывает на гомоскедастичность случайного остатка в модели (1), то есть показатель дисперсии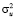 
является константой для каждого уравнения наблюдения.
В ходе теста Дарбина-Уотсона основная и альтернативная гипотеза выглядят так:
.
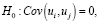
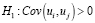Алгоритм теста Дарбина-Уотсона включает шаги:
1. По оцененной модели (2) рассчитывается статистика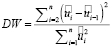 
.
2. По таблице значений статистик dL и dU критерия Дарбина-Уотсона по количеству наблюдений и входящих в модель регрессоров находятся критические значения нижней и верхней границы для статистики DW – dL и dU.
3. Смотрим в какой интервал попала статистика и делаем соответствующие выводы:
Проверим актокоррелированность случайного остатка в модели (2):
DW = 0,7077; dL = 1,36;
dU = 1,5 при k = 1, n = 30.
Статистика Дарбина-Уотсона получила близкое к 0 значение и попадает в область отклонения гипотезы H0 – случайный остаток имеет положительную автокорреляцию между соседними уровнями случайных остатков. Из этого следует, что МНК-оценки в модели (2) не являются оптимальными и причиной этому может служить возможная ошибка в спецификации модели (1). Наличие автокорреляции случайных остатков может сигнализировать о пропуске в уравнении связи важной объясняющей переменной. Так как для объяснения значений yt в модели (1) никакие факторы, кроме времени, не рассматриваются, возьмем в качестве такой переменной величину yt–1. Тогда вместо спецификации (1) будем рассматривать модель
yt = a•yt–1 + ut, (3)
которая называется моделью авторегрессии порядка p (в данном случае p = 1) AR(p).
Проверим стационарность временного ряда (3) по тесту Дики-Фуллера. иными словами проверим значение коэффициента a в формуле (3): если a = 1, то процесс имеет единичный корень и временной ряд yt является не стационарным; при |a| < 1 yt является стационарным временным рядом.
Если выражение (3) записать при помощи оператора разности первого порядка Δyt = yt – y t–1, то оно примет вид Δyt = b•yt–1 + ut, где b = a – 1. Временной ряд имеет единичный корень (является интегрированным первого порядка), если его разности первого порядка образуют стационарный ряд.
Для модели авторегрессии первого порядка суть теста Дики-Фуллера заключается в проверке гипотезы H0 о наличии единичного корня (или гипотезы о нулевом значении коэффициента b). Принятие/отклонение гипотезы H0 происходит в результате сравнения DF-статистики для коэффициентов регрессии (3) с проверочными значениями статистики, взятыми из критических таблиц МакКиннона, составленных для конкретных видов тестовых регрессий на заданном уровне значимости.
Для модели (3) без константы и тренда по тесту Дики-Фуллера DF = 2,58, что при используемом объеме выборки в 29 наблюдений позволяет отклонить гипотезу H0 и считать ряд yt стационарным, поскольку DF > DFkr = –1,95 (для 5 % уровня).
Однако предполагая возможную авторегрессию в рамках (3) не первого, а более высокого порядка, был проведен расширенный (пополненный) тест Дики-Фуллера для модели (3), в которую был добавлен лаг первой разности эндогенной переменной, который позволил принять гипотезу H0 при L = 1; для более высоких порядков лага L = 2 и L = 3 гипотеза отклоняется.
Заключение
В виду полученных противоречивых результатов теста Дики-Фуллера для модели (3), а также установленной по тесту Дарбина-Уотсона авторегрессии первого порядка остатков в модели (1), можно предположить, что остатки ut в модели (3) являются не «белым шумом», а некоторым стационарным ARMA-процессом. Использование для описания временного ряда yt смешанной модели авторегрессии и скользящего среднего ARMA(p,q) вида
yt = β0 + β1yt-1 + β2yt-2 +⋯+ βpyt–p + λ1ƺt–1 + λ2ƺt–2 +⋯+ λqƺt–q + ƺt (4)
подтвердили это допущение.
При помощи теста Бройша-Годфри была принята альтернативная гипотеза H1 о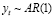 
и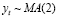 
. Построенная модель ARMA(1,2) содержит случайные влияния в виде «белого шума» (Рис. 3).
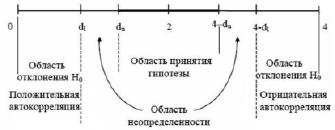
Рис. 2. Критические интервалы статистики Дарбина-Уотсона
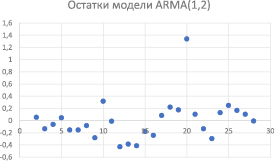
Рис. 3. График «белого шума» для смешанной модели
Наблюдаемое резкое отклонение случайного остатка при t = 20 от полученного облака точек следует рассматривать как выброс в значениях «белого шума». Анализ данных временного ряда до и после 2010 года, в котором показатели yt улучшились по сравнению с предыдущими, показал, что никаких структурных сдвигов это не вызвало, поэтому модель вида (4) можно использовать с единым набором параметров, вычисленным по всему имеющемуся набору статистики.
Состоятельные оценки параметров модели (4) получены как оценки метода наименьших квадратов, при этом β0 = 0;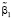 
= 0,998; 
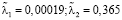. Но исследованный на значимость коэффициент λ1 указал на незначимость ƺt-1 в модели. Это говорит о том, что с учетом обратимости временного ряда (4), все происходящие события в текущем периоде отражаются на значении показателя численности населения только через два года, причем это является более существенным влиянием на эндогенный показатель, чем текущее воздействие случайных факторов, которое составляет 0,352 млн. Этот показатель почти в три раза ниже, чем в модели (2), что говорит о более высокой точности модели ARMA(1,2) и возможности её применения для автопрогнозирования в краткосрочном и среднесрочном периоде.