Введение
Перед исследователями часто возникает задача – как на основе уже имеющихся пространственно-временных наблюдений за процессом или явлением составить представление о том, каковы могли бы быть значения предстоящих наблюдений. Существенным и измеряемым свойством такого прогноза является его достоверность. В основе прогнозирования должны лежать обоснованные предположения о тех характеристиках (или механизмах) процессов, с которыми можно связать меняющиеся данные. Эти предположения формулируются как модели – от эвристических до математических, при этом методы исследования можно подразделять на интуитивные и формализованные. [1]. В настоящей работе нами рассматривается формализованный метод – метод спектрального оценивания с использованием рядов Прони [2]. На основе применения этого метода строится модель временного ряда, она опробуется на тестовых последовательностях и используется для прогноза поведения некоторых экономических показателей.
Задачи анализа числовых рядов и задачи прогноза числовых рядов, вообще говоря, различны. Каждое из этих направлений имеет свои традиции в исследованиях, свои наработанные методы решения [3]. Так, одной из актуальных задач анализа числовых данных является выделение характерных особенностей, признаков, позволяющих идентифицировать конкретный набор данных для его последующей классификации [4-5]. При решении задач прогноза поведения числовых рядов исследователей интересуют не столько собственно особенности поведения того или иного подмножества данных, сколько выявление таких атрибутов числовых рядов, которые позволяют оценить значения рядов вне области наблюдения. [6-7]. При этом существуют такие методы прогноза (например – метод скользящего среднего), которые вряд ли могут быть применены для анализа. С другой стороны, такие практические методы анализа, как, например, режекторная фильтрация, не могут быть непосредственно использованы при прогнозе.
Но можно выделить одну группу методов, общую как для анализа, так и для прогноза, а именно – методы спектрального оценивания. Они продуктивно используются в теоретических и практических исследованиях для широкого круга задач анализа и прогноза числовых рядов [2].
Опыт применения преобразования Фурье (ПФ) при прогнозе временных рядов рассмотрен в ряде работ [2, 8-11]. Анализ этих работ показывает, что непосредственно прогноз с применением ПФ невозможен. Поясним это на простом примере: пусть прямое ПФ выполняется для некоторого временного ряда y(t), содержащего N точек. Очевидно, что при выполнении обратного ПФ значения будут повторяться через каждые N отсчетов. Таким образом, как отмечает автор [10], при использовании ПФ «любой прогноз является точным повторением временного ряда с его начала». Отсюда становится понятным, что непосредственное применение спектров Фурье для задач прогноза невозможно – начальные значения ряда лишь в специально оговариваемых случаях могут быть близки к прогнозируемым величинам.
Предлагаемое в настоящей работе преобразование Прони лишено этого недостатка. Оно по сути своей является методом спектрального оценивания, имеет приближенный характер и может быть непосредственно использовано при прогнозе.
Метод Прони
Преобразование Прони (ПП), как и преобразование Фурье, основано на разложении функции в ряд. ПП, в отличие от ПФ, не является спектральным преобразованием в чистом виде, а является способом оценивания (как метод наименьших квадратов) дискретных данных с помощью линейной комбинации экспоненциальных комплексно-значных функций.
Автор этого подхода, Гаспар Рише (барон де Прони), исследуя законы расширения различных газов, пришел в 1795 году к выводу о возможности представления этих законов в виде ряда, членами которого являются затухающие экспоненты [12]. Современные модификации этого подхода обобщены на модель, в которых слагаемыми ряда являются затухающие синусоиды [2, 13, 14]. Именно такая модель и рассмотрена в настоящей статье.
Кратко суть метода в следующем. Пусть имеется n-1 значений временного ряда y(i), число n лежит в некотором диапазоне наблюдаемых данных 1 ≤ n ≤ N. Тогда значение y(n) можно спрогнозировать следующей суммой из p слагаемых (эту сумму еще называют p-членной моделью комплексных экспонент [2]):
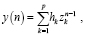 (1)
(1)
где множители hk и zk в общем случае комплексны и определяются выражениями
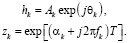 (2)
(2)
Обозначения в выражениях (2) общеприняты: A, θ, α, f – это амплитуда, фаза (в радианах), затухание (в с-1)и частота (в Гц) k-го слагаемого соответственно.
В самом общем случае выражения (1)-(2) определяют задачу спектрального оценивания по методу Прони для произвольных, в том числе и комплексных, значений ряда. Для задач экономического прогноза естественно предположить, что наблюдаемые данные y(i) – это действительные числа. В этом случае формула (2) для каждой комплексной экспоненты будет содержать её комплексно-сопряжённую пару и ряд (1) примет вид
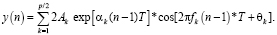 (3)
(3)
Здесь важно подчеркнуть усечённый характер ряда в формуле (3) по сравнению с рядом (2) – членов ряда стало в два раза меньше (p/2 вместо p) именно в силу комплексной сопряженности слагаемых.
Одной из характеристик метода Прони является то, что его можно отнести к методам авторегрессии [2, 14]. Ранее автор применял этот подход, дополнив его фильтрацией в скользящем окне (АРСС), при моделировании влияния систем трещин в твёрдых телах на отраженный акустический сигнал в задачах дефектоскопии [15], а также при изучении трансформации сейсмических сигналов при прохождении зон вероятного затухания в задачах разведочной геофизики [16].
Подробнее применение метода Прони рассмотрим на модельных данных. Для более компактного представления результатов рассмотрим небольшую совокупность данных – 21 точку. График наблюдений представлен на рис. 1. Генезис этих данных не играет принципиальной роли и в дальнейшем не обсуждается.
Возьмём из этих данных 16 точек – первое окно обработки (рис. 2), выполним ПП, порядок преобразования p = 7.
В результате получим 7*4=28 результирующих параметров (таблица 1).
В таблице 1 в первом столбце даны порядковые номера слагаемых разложения по формуле (3). Представляется логичным отсортировать результат ПП по возрастанию частот во втором столбце. Это связано с тем, что, в отличие от ПФ, при ПП увеличение номера гармоники не влечёт за собой увеличение значения частоты. Сортировка позволяет лучше представить вклад каждой гармоники в итоговое разложение.
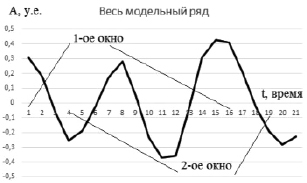
Рис. 1. Модельный ряд. Обозначены границы первого и второго окон обработки.
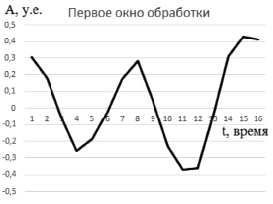
Рис. 2. Первое окно обработки
Таблица 1
Результат ПП для первого окна обработки
|
№ слагаемого ПП |
Частота, Гц |
Затухание, 1/сек |
Амплитуда, у.е. |
Фаза, рад. |
|
3 |
-0,35571 |
0,01223 |
0,01373 |
3,12106 |
|
4 |
-0,14391 |
0,01002 |
0,13788 |
-0,09935 |
|
7 |
-0,07425 |
0,14921 |
0,01355 |
1,0571 |
|
1 |
0 |
-8,24433 |
0,04583 |
0 |
|
6 |
0,07425 |
0,14921 |
0,01355 |
-1,0571 |
|
5 |
0,14391 |
0,01002 |
0,13788 |
0,09935 |
|
2 |
0,35571 |
0,01223 |
0,01373 |
-3,12106 |
Обратим внимание на столбец «Частота». В случае спектров Фурье каждой гармонике соответствует частота, определяемая, с одной стороны, теоремой Котельникова [17], а с другой стороны – числом точек в окне преобразования. Поэтому для любых 16-ти отсчетов модельного ряда в случае ПФ выполняются следующие два условия: 1) число гармоник и набор частот будут неизменны, и 2) шаг по частотам постоянен. В случае же ПП эти утверждения не имеют место. То, что шаг по частотам неравномерен, видно уже из таблицы 1. Для проверки первого условия сдвинем окно обработки на 3 отсчета вправо (отсчеты с 4 по 19). Полученная часть модельного ряда приведена на рис. 3, а на рис. 1 помечены границы как первого, так и второго окон обработки).
Очевидно, что число точек в окне осталось прежним – 16, шаг по времени так же остался прежним. Спектр Фурье в этом случае изменится по значениям, но число гармоник и шаг по частоте останутся, очевидно, прежними. Результат ПП показан в таблице 2.
Из сопоставления таблиц 1 и 2 хорошо видно, что для каждого номера гармоники (первый столбец таблиц) получаются различные значения частот (второй столбец). В этом и заключается главное отличие метода Прони от метода Фурье. Именно поэтому вычисление спектра Прони – это дополнительная процедура, не являющаяся непосредственно целью ПП. В настоящей работе вопросы вычисления спектра Прони не рассматриваются, алгоритм приводится, например, в [2].
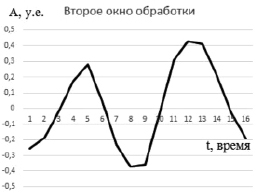
Рис. 3. Второе окно обработки
Таблица 2
Результат ПП для второго окна обработки
|
№ слагаемого ПП |
Частота, Гц |
Затухание, 1/сек |
Амплитуда, у.е. |
Фаза, рад. |
|
3 |
-0,35888 |
-0,03045 |
0,01822 |
2,9073 |
|
4 |
-0,1553 |
-0,02756 |
0,13574 |
-2,35662 |
|
7 |
-0,09742 |
0,15036 |
0,03178 |
1,04873 |
|
1 |
0 |
-1,17644 |
0,06255 |
3,14159 |
|
6 |
0,09742 |
0,15036 |
0,03178 |
-1,04873 |
|
5 |
0,1553 |
-0,02756 |
0,13574 |
2,35662 |
|
2 |
0,35888 |
-0,03045 |
0,01822 |
-2,9073 |
Прогнозирование значений индекса потребительских цен на товары и услуги с помощью ПП
Одним из важнейших числовых показателей в макроэкономике, наряду с ВВП, является индекс потребительских цен на товары и услуги (ИПЦ) [18]. Для решения различных задач применяются несколько разных подходов к вычислению ИПЦ – по отношению к предыдущему месяцу, к декабрю предыдущего месяца и.т.п. В настоящей работе анализируются данные ИПЦ двух типов – ИПЦ в % по отношению к аналогичному месяцу предыдущего года и ИПЦ в % по отношению к предыдущему месяцу.
Значения ИПЦ, рассчитанные как % к соответствующему месяцу предыдущего года, взяты с сайта Росстата (данные находятся в открытом доступе на главной странице сайта Федеральной службы государственной статистики (Росстата) [19]. В таблице 3 данные приведены помесячно с 1 января 2017 года и до текущего месяца (на момент проведения расчетов были доступны данные за июнь 2020).
Значение MAE (средняя абсолютная ошибка) = 0,125 вычислялось по обычной формуле:
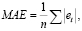 (4)
(4)
здесь n – текущее значение базы прогноза (в данном случае все фактические значения до момента времени t-1), t – прогнозируемая точка, |et| – абсолютная величина ошибки прогноза в точке.
Данные таблицы 3 представим в графическом виде, при этом будет дана сразу окончательная база ПП – 42 точки: (это по 12 точек за 2017-2019 годы и еще за 6 месяцев текущего, 2020, года). На рис. 4 фактические данные показаны сплошной линией (кривая ИПЦ с сайта Росстата [19]), а результат ПП – штриховой линией. Метод Прони правильно отслеживает характер поведения показателя, но локальные выбросы сглаживает. Отсюда и довольно высокое значение MAE – около 12,5 %.
Таблица 3
Данные Росстата [19] по индексу потребительских цен. Курсивом показаны результаты ПП
|
2017 год |
2018 год |
2019 год |
2020 год |
||||
|
105,04 |
105,0685 |
102,19 |
102,286 |
104,99 |
104,8867 |
102,42 |
102,6617 |
|
104,06 |
104,0804 |
102,18 |
102,0139 |
105,22 |
105,0331 |
102,31 |
102,4703 |
|
104,25 |
104,2285 |
102,35 |
102,1635 |
105,25 |
105,0563 |
102,54 |
102,7449 |
|
104,14 |
104,119 |
102,4 |
102,1005 |
105,17 |
105,1132 |
103,09 |
102,8536 |
|
104,09 |
104,213 |
102,41 |
102,2312 |
105,13 |
104,96 |
103,02 |
102,931 |
|
104,35 |
104,5183 |
102,29 |
102,2676 |
104,66 |
104,7078 |
103,21 |
103,16 |
|
103,86 |
103,8942 |
102,5 |
102,5675 |
104,58 |
104,5559 |
MAE |
0,1252 |
|
103,27 |
103,2843 |
103,6 |
103,5112 |
104,31 |
104,161 |
||
|
102,96 |
103,0404 |
103,38 |
103,6618 |
103,99 |
103,8096 |
||
|
102,72 |
102,8206 |
103,54 |
103,7476 |
103,75 |
103,6714 |
||
|
102,49 |
102,6764 |
103,83 |
104,0079 |
103,53 |
103,4086 |
||
|
102,51 |
102,7192 |
104,26 |
104,3579 |
103,04 |
103,1246 |
||
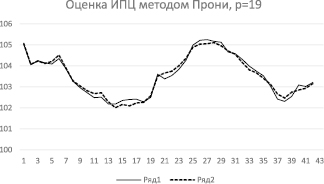
Рис. 4. Сравнение фактической кривой ИПЦ (данные Росстата, [19], сплошная линия) и результата настоящей работы, штриховая линия
Для ряда действительных данных из N точек для оценивания методом Прони порядок оценивания p лежит в интервале 3 ≤ p ≤ (N-1)/2 и должен быть нечетным числом [2] (это должно быть понятно из структуры таблиц 1 и 2). В случае N = 42 порядок оценивания равен 19. Ряд (3) при этом имеет 10 различных слагаемых: одно слагаемое соответствует нулевой частоте, и (p-1)/2 слагаемых в случае действительных чисел входят в формулу (3) парами. В таблице 4 приводятся коэффициенты ПП для данных по ИПЦ.
В таблице 4 данные отсортированы по возрастанию частоты (второй столбец), поэтому для понимания работы ПП, так же, как и в таблицах 1 и 2, добавлен первый столбец – истинные порядковые номера слагаемых ряда (3). Характерными для окна преобразования являются гармоники № № 12, 2 и 5, они, наряду с статической составляющей (гармоника № 8) дают максимальный по амплитуде вклад в динамику кривой.
Обратимся теперь непосредственно к процедуре прогноза. Метод Прони не так часто используется вообще, и для экономического прогноза – в частности, поэтому необходимо иметь возможность количественного сравнения результатов нашего прогноза с опубликованными данными. Для этой цели были взяты данные Центра макроэкономического прогнозирования (ЦМП) Высшей школы экономики [20]. Ими выполняется помесячный прогноз, в частности, для ИПЦ, вычисленных в % по отношению к предыдущему месяцу.
Нами для прогноза взяты данные, начиная с августа 2018 года – именно эти числа доступны по ссылке [20] на момент проведения расчетов. На сайте [20] представлены фактические данные Росстата [19] и прогноз ЦМП ВШЭ с августа 2018 года по апрель 2020 года за исключением июля 2019 года (без объяснения причин). По методу Прони были спрогнозированы 21 значения (включая июль 2019 года), затем наши оценки и оценки ЦМП были сопоставлены. Результаты сведены в таблицу 5.
Таблица 4
Результат ПП для ИПЦ, p = 19
|
№ слагаемого ПП |
Частота, Гц |
Затухание, 1/сек |
Амплитуда, у.е. |
Фаза, рад. |
|
8 |
0 |
0,00029 |
102,9374 |
0 |
|
12 |
0,04163 |
0,0065 |
0,58378 |
-0,57322 |
|
16 |
0,08462 |
-0,0278 |
0,11075 |
-1,41009 |
|
1 |
0,14545 |
0,02353 |
0,04798 |
1,22977 |
|
5 |
0,2071 |
-0,02644 |
0,14393 |
-0,50415 |
|
9 |
0,25409 |
-0,00964 |
0,04348 |
0,38475 |
|
13 |
0,33074 |
-0,07733 |
0,07498 |
-1,2134 |
|
2 |
0,36566 |
-0,07625 |
0,18902 |
0,16166 |
|
6 |
0,41886 |
-0,04389 |
0,07732 |
0,43284 |
|
10 |
0,46589 |
-0,00092 |
0,0374 |
-0,08036 |
Таблица 5
Сравнение двух прогнозов ряда ИПЦ
|
Факт |
Прони |
ЦМП |
ΔПрони |
ΔЦМП |
|
100,01 |
100,46 |
99,83 |
0,446 |
0,18 |
|
100,16 |
100,36 |
100,32 |
0,204 |
0,16 |
|
100,35 |
100,38 |
100,34 |
0,027 |
0,01 |
|
100,50 |
100,38 |
100,45 |
0,116 |
0,05 |
|
100,84 |
100,51 |
100,71 |
0,331 |
0,13 |
|
101,01 |
100,66 |
101,06 |
0,349 |
0,05 |
|
100,44 |
100,56 |
100,67 |
0,122 |
0,23 |
|
100,32 |
100,55 |
100,35 |
0,233 |
0,03 |
|
100,29 |
100,59 |
100,33 |
0,301 |
0,04 |
|
100,34 |
100,43 |
100,38 |
0,092 |
0,04 |
|
100,04 |
100,45 |
100,39 |
0,409 |
0,35 |
|
100,20 |
100,21 |
100,39 |
0,012 |
0,19 |
|
99,76 |
100,26 |
100,15 |
0,502 |
0,39 |
|
99,84 |
100,12 |
100,05 |
0,278 |
0,21 |
|
100,13 |
100,15 |
99,76 |
0,019 |
0,37 |
|
100,28 |
100,45 |
100,32 |
0,168 |
0,04 |
|
100,36 |
100,5 |
100,57 |
0,142 |
0,21 |
|
100,40 |
100,49 |
100,66 |
0,092 |
0,26 |
|
100,33 |
100,36 |
100,17 |
0,03 |
0,16 |
|
100,55 |
100,37 |
100,39 |
0,177 |
0,16 |
|
100,83 |
100,52 |
100,45 |
0,307 |
0,38 |
|
MAE |
0,2074 |
0,1733 |
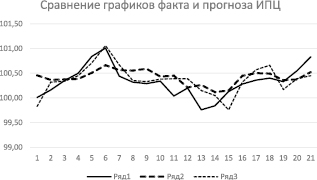
Рис. 5. Сравнение графиков ИПЦ – фактические данные Росстата (ряд 1), прогноз методом Прони (ряд 2) и прогноз ЦМП ВШЭ [20]
Эти же данные приведены на графике (рис. 5). Видно, что с увеличением базы, начиная с 15-16 значения, прогноз по ПП становится достаточно адекватным. Сравнивая значения рассчитанных средних абсолютных ошибок (0,2074 для ПП и 0,1733 для ЦМП), можно сделать вывод о неплохом соответствии прогноза по ПП и опубликованных данных от ЦМП ВШЭ.
Здесь нужно подчеркнуть различие в методиках прогноза, выполняемого по методу Прони в настоящей работе, и прогноза, выполняемого в ЦМП НИУ ВШЭ. Прогноз с помощью ПП выполняется только лишь на основе имеющегося временного ряда. Никакие иные факторы прошлых периодов, существующие данные и модели, предположения о трендах и внешних воздействиях не учитываются. Эта та самая чистая модель временного ряда, про которую авторы [21] писали « These are the work-horse of the forecasting industry…». Свои же прогнозы ЦМП выполняет по нескольким моделям [20], учитывающим самые разнообразные факторы. В этом смысле недостатки и достоинства метода Прони очевидны. Мы не можем, используя ПП, улучшить прогноз, учитывая вновь появившиеся прямые и косвенные данные, способствующие более точному пониманию генезиса числовых значений. С другой стороны, ценность прогноза, не учитывающего известные уже предстоящие факторы, может оказаться невелика, но простота в получении результатов прогноза может оказаться решающим фактором.
Заключение
В работе описан метод Прони. Показаны некоторые особенности преобразования Прони, поведение его составляющих, отличие преобразования Прони от преобразования Фурье. Выполнено приближение поведения кривой индекса потребительских цен на товары и услуги с помощью ряда Прони. Для сравнения с опубликованными данными выполнен помесячный прогноз ИПЦ, вычисленного в % по отношению к предыдущему месяцу. Показана сопоставимость результатов прогноза по методу Прони и прогноза по методикам ЦМП НИУ ВШЭ.
Автор данной работы считает, что преобразование Прони может представлять интерес как в сугубо теоретическом смысле, так и при выполнении практических задач анализа и прогноза в экономике.

