Введение
В настоящее время все большее количество лиц, располагающих временно свободными денежными средствами и желающих их сохранить и преумножить, обращают свое внимание на возможность инвестирования в различные биржевые активы (ценные бумаги российских и иностранных эмитентов, валюту, фьючерсы).
Торговля на бирже дает большие возможности по увеличению капитала, однако, следует отметить, что и риски также велики.
Для ведения успешной торговли на финансовых рынках необходимо знать закономерности динамики котировок на биржевые активы, а также уметь использовать эти знания для принятия решений, относительно покупки или продажи того или иного актива.
В настоящее время существуют и развиваются два основных направления в исследовании фондовых рынков: фундаментальный и технический анализы.
Первый подход к анализу заключается в выявлении недооценных или переоцененных ценных бумаг, что связано с изучением факторов экономической, социальной, политической природы, влияющих на финансовые и товарные рынки. Как правило, данный анализ носит качественный характер, хотя и базируется на количественных данных.
Технический же анализ напротив исходит из формальной обработки информации, относящейся к динамике цен активов, без учета влияния факторов, породивших эти изменения. Иными словами, технический анализ – исследование прошлой динамики финансовых рынков математическими и статистическими методами с целью прогнозирования будущего направления движения цен.
Очевидно, что оба подхода имеют как свои достоинства, так и недостатки.
Цель исследования
Цель настоящего исследования состоит в создании инструмента прогнозирования направления движения биржевых цен на основе применения теории вероятностей и математической статистики.
В соответствии с поставленной целью были сформулированы следующие задачи:
1. Разработка методики оценки вероятности направления движения цен биржевых активов с использованием методов теории вероятностей и математической статистики.
2. Создание на основе полученной методики индикатора тренда в одной из программ технического анализа.
3. Формулировка правил принятия решений относительно покупки/продажи биржевых активов с использованием разработанного технического индикатора.
4. Апробирование на исторических данных полученных индикатора и правил принятия решений, разработанных на его основе.
Материалы и методы исследования
Для успешной работы на финансовых рынках не обязательно знать точное значение цены того или иного актива в некоторый будущий момент времени Т. Достаточно иметь возможность определить направление движения цены. Очевидно, что возможны три таких направления:
1. Рост – когда цена в момент времени Т окажется больше текущей цены: ST > S0.
2. Отсутствие изменений – цена в момент времени Т будет равна текущей цене: ST = S0.
3. Снижение (Падение) – цена через время Т окажется ниже текущей цены: ST < S0.
С целью упрощения для дальнейших рассуждений три указанных выше сценария развития были сведены к двум:
1. Цена вырастет: ST > S0.
2. Цена не вырастет: ST ≤ S0.
Несомненно, что модель, используемая с целью прогнозирования, должна отражать некоторые свойства динамики биржевых цен. Рассмотрим основные из них [1].
Во-первых, изменение цен – не случайно, оно подчинено некоторым тенденциям. Однако, сила, направление и продолжительность этих тенденций заранее неизвестны. Если цена, например, стала расти, то мы не знаем, как долго это будет продолжаться и до какого значения она вырастет.
Во-вторых, распределение доходности (приростов цен) сильно отличается от нормального. Оно несимметрично и имеет существенный эксцесс (оно вытянуто в центральной части, имеет более толстые «хвосты»).
В третьих, волатильность приростов цен (доходности) зависит от времени и образует так называемые кластеры, когда период низкой волатильности сменяется периодом высокой волатильности и наоборот.
В четвертых, отсутствие зависимости между соседними доходностями (приростами цены).
Рассмотренные свойства по-разному находят свое отражение в существующих моделях временных рядов финансовых активов.
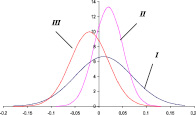
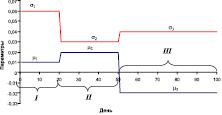
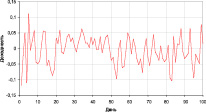
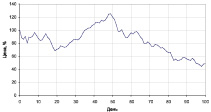
Рис. 1. Предлагаемый подход для описания динамики цен акций
Так, например, зависимость волатильности от времени часто описывается обобщенной авторегрессионной моделью с условной гетероскедастичностью (GARCH – моделью) [1, 2]:
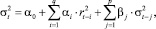
где α0, αi, βj – параметры модели; r – приросты цены; σ – СКО (волатильность); q, p – порядок модели для членов r2 и σ2 соответственно.
Распределение доходности, отличное от нормального, можно аппроксимировать семейством нормальных распределений с различными параметрами, распределением Лапласа или обобщенным экспоненциальным распределением следующего вида (рис. 5) [3]:
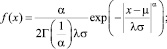
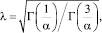
где α – параметр распределения.
Однако все эти подходы хорошо описывают указанные выше свойства финансовых временных рядов по отдельности, но не все вместе.
В данной работе предлагается подход, согласно которому приросты цен (доходности) считаются независимыми и распределенными по нормальному закону. При этом параметры этого распределения зависят от времени и представляют собой кусочно-постоянные функции. На рис. 1 показан смоделированный ряд цен актива. Весь период разбит на три интервала времени, обозначенные как I, II и III. В каждом интервале приросты цен моделировались по нормальному закону распределения. При этом параметры этого распределения в каждом периоде были своими.
По нашему мнению, такая модель позволяет описать сразу большинство наблюдаемых свойств финансовых временных рядов, а именно: тренды, зависимость волатильности от времени, отличие распределения приростов цен от нормального, независимость приростов цен.
Очевидно, что любое прогнозирование должно опираться на какую-либо модель изучаемого процесса.
Процесс ценообразования на финансовых рынках чаще всего описывают моделью геометрического броуновского движения [1]. В более общем случае предполагается, что параметры модели, такие как доходность (μ) и волатильность (σ), зависят не только от времени, но и от цены актива:
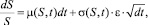
где S – цена биржевого актива; t – время; μ(S, t) – доходность (средняя); σ(S, t) – волатильность доходности; ε ~ N(0,1) – нормально распределенная случайная величина с математическим ожиданием 0 и СКО, равным единице.
На практике же зависимость этих параметров от цены не подтверждается, поэтому используется более простая версия (модификация) модели:
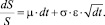
В случае, когда параметры модели μ и σ являются константами, существует достаточно простое решение стохастического дифференциального уравнения, описывающего геометрическое броуновское движение:
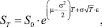
где S0 – цена биржевого актива в начальный момент времени; ST – цена биржевого актива в некоторый момент времени T.
Не смотря на то, что факты говорят о непостоянстве μ и σ данное решение будет использовано далее. При этом будем предполагать, что состояние рынка, описываемое параметрами μ и σ, будет меняться не непрерывно, а скачкообразно. То есть можно будет выделить отрезки времени, на которых выше указанные параметры будут постоянны.
Введем в рассмотрение следующую величину:
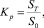
которая представляет собой коэффициент роста цены за период времени T.
Тогда
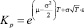
или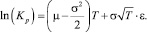 
Таким образом, логарифм коэффициента роста цены имеет нормальное распределение
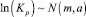
с параметрами
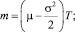
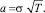
Сам же коэффициент роста, очевидно, имеет логарифмически нормальное распределение с теми же параметрами:
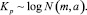
Функция плотности и данного распределения имеет вид:
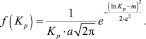
Интегральная функция логарифмически нормального распределения коэффициента роста цены определится следующим образом:
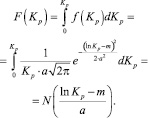
Данная функция позволяет определить вероятность направления движения цены актива. Так, вероятность снижения цены:
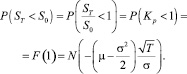
Соответственно, вероятность роста цены:
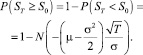
При определенном соотношении параметров будем иметь ситуацию неопределенность в отношении направления движения цены: вероятность роста будет равна вероятности снижения и равна 0,5:
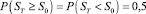
при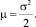 
Для принятия решения покупке/продаже того или иного биржевого актива достаточно иметь прогноз на 1 период времени вперед. В качестве такого периода может выступать, например, 1 час, 1 день, 1 неделя. Все зависит от тех данных, которые мы используем для построения прогноза.
Формулы оценки вероятности снижения и роста цены на 1 шаг вперед будут иметь вид:
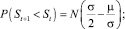
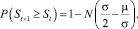
Собственно эти формулы и будут использоваться далее.
Как видно из полученных ранее формул вероятность роста/снижения цены зависит от двух параметров: μ и σ. Таким образом, прогнозирование вероятности направления движения цены актива в конечном итоге сводится к оценке μ и σ на основе фактических данных. Очевидно, что для оценки значений параметров распределения следует использовать методы математической статистики.
На некоторый текущий момент времени в наличии будет ряд цен S длиной n. На основе этих данных можно вычислить n – 1 значение прироста цен:
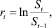t = 2, ..., n.
По первым k значениям могут быть рассчитаны начальные значения параметров μ и σ:
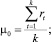
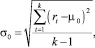
где k << n.
В качестве средства оценки изменения параметров μ и σ в данной работе будет использоваться один из методов последовательного статистического анализа – метод кумулятивных сумм [5]. Применение данного метода в финансовой сфере уже описывался в литературе [6].
Метод кумулятивных сумм состоит в следующем. На первом этапе выдвигаются две гипотезы:
1. Основная (Н0), заключающаяся в том, что изменение параметра не произошло (значение доходности ri принадлежит распределению с параметром θ0).
2. Конкурирующая (Н1), состоящая в том что изменение параметра произошло (значение ri принадлежит распределению с параметром θ1).
На втором этапе, на каждом временном шаге рассчитываются логарифмы отношения правдоподобия:
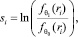
где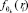 
– функция плотности распределения при значении параметра θk; θ0 – значение параметра до изменения; θ1 – значение параметра после изменения.
Если принять во внимание допущение о том, что распределение доходности описывается нормальным законом, то могут быть получены следующие формулы логарифма отношения правдоподобия.
При оценке изменения параметра μ:
где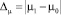 
– задаваемое минимальное обнаруживаемое абсолютное изменение параметра μ.
Параметр μ может измениться как в большую, так и в меньшую сторону. Поэтому следует рассмотреть два варианта выражения для логарифма отношения правдоподобия.
1. Если μ1 > μ0, то
μ1 = μ0 + Δ и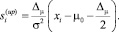 
2. Если μ1 < μ0, то
μ1 = μ0 – Δ и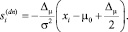 
При оценке изменения параметра σ:
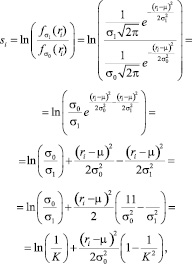
где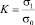 
– задаваемое минимальное обнаруживаемое относительное изменение параметра σ.
Так как параметр σ может измениться как в большую сторону, так и в меньшую, то представим K следующим образом:
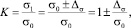
где Δσ – задаваемое минимальное обнаруживаемое абсолютное изменение параметра σ.
Таким образом, в случае, если предполагается увеличения параметра σ, следует использовать
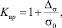
иначе
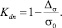
На основе логарифмов отношения правдоподобия вычисляется собственно кумулятивная сумма, давшая названию методу:
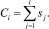
Поскольку изучается изменение двух параметров, то на каждом временном шаге необходимо рассчитывать 4 значения кумулятивной суммы: два значения для параметра μ (для оценки изменения в большую и меньшую стороны) и два значения для параметра σ.
Исходя из кумулятивной суммы, получается, так называемая, решающая функция G, значение которой позволяет принять или отклонить выдвинутую ранее гипотезу:
Gi = Ci – M,
где M – минимум кумулятивной суммы:
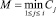
или
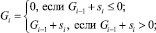G0 = 0.
Если Gi ≥ h – то гипотеза H1 отвергается, где h – задаваемый пороговый уровень.
Работу метода кумулятивных сумм при обнаружении изменения волатильности иллюстрирует рис. 2.
После обнаружения изменений значения параметров распределения пересчитываются по формулам:
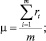
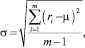
где m – число периодов, прошедших с последнего момента, когда соответствующая кумулятивная сумма принимала экстремальные значения (была минимальной/максимальной).
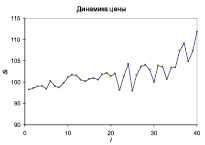
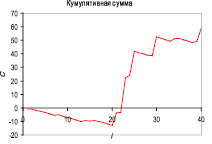
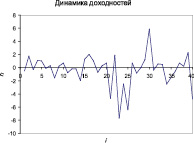
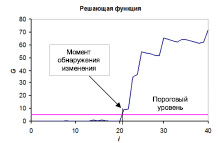
Рис. 2. Обнаружение изменения волатильности с помощью метода кумулятивных сумм
Алгоритм оценки вероятности направления будущего движения цен биржевых активов представлен в виде укрупненной блок-схемы (рис. 3).
На блок-схеме приняты следующие условные обозначения:
Δμ , Δσ – задаваемые минимальные обнаруживаемые абсолютные изменение параметров μ и σ соответственно;
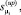
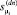– логарифмы отношения правдоподобия при определении изменения параметра μ в большую и меньшую сторону соответственно;
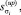
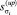– логарифмы отношения правдоподобия при определении изменения параметра σ в большую и меньшую сторону соответственно;
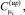
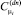– кумулятивные суммы при определении изменения параметра μ в большую и меньшую сторону соответственно;
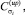
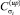– кумулятивные суммы при определении изменения параметра σ в большую и меньшую сторону соответственно;
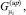
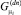– решающие функции при определении изменения параметра μ в большую и меньшую сторону соответственно;
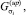
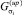– решающие функции при определении изменения параметра σ в большую и меньшую сторону соответственно;
hμ, hσ – задаваемые пороговые уровни при определении изменений параметров μ и σ соответственно.
Полученную методику было решено реализовать ее в одном из профессиональных пакетов технического анализа. К настоящему времени разработано много программных средств технического анализа финансовых рынков. Среди них можно назвать WealthLab, Ami Broker, TS Lab, Meta Trader, Meta Stock. Все они имеют свои положительные и отрицательные качества.
В данной работе было решено использовать пакет Meta Stock как относительно распространенное и простое в использовании средство технического анализа.
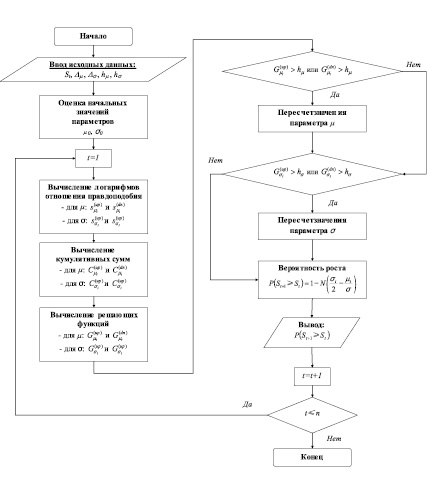
Рис. 3. Блок-схема алгоритма оценки вероятности роста цен биржевых активов
На пути переноса выше рассмотренной методики в пакет технического анализа возникли некоторые технические трудности, связанные с тем, что Meta Stock обладает недостаточно гибким языком программирования для описания сложных алгоритмов. В частности, в нем отсутствуют операторы цикла. Недостаточно хорошо разработан условный оператор. Плохо реализована работа с массивами.
Выход из создавшейся ситуации был найден с помощью динамически подключаемой библиотеки (DLL), разработанной частным трейдером из Санкт-Петербурга, Сергеем Коссинским [7]. Эта библиотека позволяет писать тексты программ на языке Python и далее использовать их в MetStock как функции пользователя при разработке индикаторов, торговых систем, советников (рис. 4).
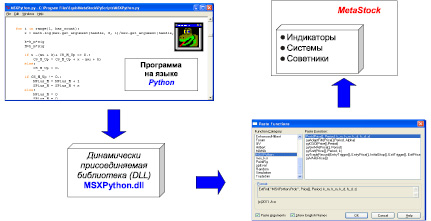
Рис. 4. Реализация методики в пакете MetaStock
Результаты исследования и их обсуждение
На основе выше описанной методики оценки вероятности направления движения цены в программе технического анализа MetaStock был создан индикатор, названный «Вероятность роста». Предназначение данного индикатора состоит в идентификации направления тренда. В качестве условий, определяющих направление тренда, были приняты следующие:
1. Восходящий («Бычий») тренд (рост цен): P(Kp > 1) > 0,5.
2. Нисходящий («Медвежий») тренд (снижение цен): P(Kp > 1) < 0,5.
При использовании индикатора «Вероятность роста» в качестве торговых сигналов на покупку/продажу предлагается использовать смену направления тренда:
1. Покупка при выполнении условия (смена нисходящего тренда на восходящий):
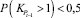и 
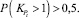
2. Продажа при выполнении условия (смена восходящего тренда на нисходящи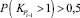й):
и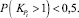 
Работа индикатора приведена на рис. 5. На данном рисунке представлен график, описывающий динамику дневных цен акций ОАО «Газпром», разбитый на зоны бычьего и медвежьего трендов в соответствии с выше указанными условиями, а также график изменения вероятности роста цены. Кроме того, на рис. 5, показаны торговые сигналы на покупку/продажу.
Визуальный анализ полученных результатов позволяет сделать следующие выводы. За редкими исключениями в соответствии с ранее описанной теорией высокие значения вероятности роста действительно соответствуют участкам роста цены, низкие значения вероятности роста приходятся на участки падения цены. Полученный в данной работе индикатор, как и всякий индикатор тренда, правильно отслеживает наличие тенденций в периоды сильных, продолжительных ценовых движений, но не очень хорошо работает в периоды неопределенности, когда цены колеблются относительно некоторого уровня, или же, когда присутствуют резкие возвратные скачки цен (например, сначала за текущий день цена резко возрастает, а затем, на следующий день, она также резко падает). Таким образом, в периоды так называемого «бокового» тренда разработанный индикатор дает ложные сигналы.
Кроме того, данный индикатор является запаздывающим. Не смотря на то, что как было уже отмечено, он хорошо отслеживает сильные тренды, он не даёт возможность купить актив в самом начале тренда (по минимальной цене), а продать в самом конце (по максимальной цене).
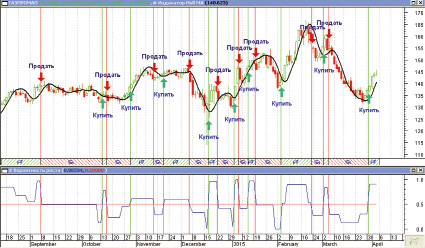
Рис. 5. Работа индикатора «Вероятность роста»
Заключение
Для создания полноценной, работоспособной системы принятия торговых решений на биржевых рынках указанные выше правила покупки/продажи следует дополнить следующими элементами:
1. Фильтры. Их основное назначение отсеивать ложные торговые сигналы, выдаваемые индикатором.
2. Ограничители потерь (так называемые, stop loss). Предназначены для выхода из сделки с некоторым небольшим, заранее определенным убытком в случае, если прогноз в отношении динамики цены не оправдался.
3. Подсистема управления капиталом. Данная подсистема необходима для определения доли имеющегося капитала при осуществлении конкретной сделки покупки/продажи.
4. Правила управления открытой позицией. Они необходимы для изменения размера открытой позиции.
Можно надеяться, что рассмотренный подход к оценке вероятности направления будущего движения цен биржевых активов займет достойное место среди арсенала средств анализа финансовых рынков и методов принятия торговых решений.