Научный журнал

Вестник Алтайской академии экономики и права

Print ISSN 1818-4057

Online ISSN 2226-3977

Перечень ВАК

Введение

Соединенные Штаты Америки являются развитой капиталистической державой со значительным потенциалом развития и огромной производственной мощью. Эта огромная страна во всех смыслах, наделенная природными ресурсами, сегодня остается наиболее экономически развитым государством.

Каждое государство имеет свои характерные факторы развития и США не являются исключением в этом отношении. Огромная территория (9,8 миллиона квадратных километров), огромный потребительский рынок (население – более 327 миллионов человек), богатство природных ресурсов, развитые рыночные отношения являются факторами, способствовавшими экономическому прогрессу.

Располагаясь вдали от театров военных действий, Соединенные Штаты не подвергались ударам мировых войн, а, наоборот, использовали их в качестве мощного фактора расширения рынков. В ходе время второй мировой войны государство увеличило свой экономический потенциал в два раза оставив далеко позади своих конкурентов из Японии и Западной Европы, став абсолютным лидером.

В настоящий момент США являются экономически высокоразвитым государством со сложной экономической географией. Сохраняя свое лидерство в международной политике и области научно-технического прогресса, эффективно используя трудовые и внутренние природные ресурсы, а также международное разделение труда и укрепляя глобальную интеграцию, она занимает первое место в мире по объему ВВП (21,44 трлн долл. США в 2019 году), существенно опередив Китайскую Народную Республику располагающуюся на втором месте (14,14 трлн долл. США в 2019 году).

ВВП отдельных штатов не уступает ВВП многих стран: Калифорния со своими 3 трлн долл. в 2018 году сопоставима с Индией (2,72 трлн долл. в 2018 году) или Соединенным Королевством (2,83 трлн долл. в 2018 году), Техас с Испанией (1,43 трлн долл. в 2018 г.) и Израилем (0,38 трлн долл. в 2018 г.) вместе взятыми, а Пенсильвания (0,78 трлн долл. в 2018 г.) превосходит Саудовскую Аравию (0,78 трлн долл. в 2018 г.). О высоком уровне экономического развития в США также свидетельствует размер ВВП на душу населения – 65,1 тысячи долларов, по данному показателю страна входит в десятку лучших результатов.

Как видно из рисунка 1, годовой рост ВВП США по итогам 4 квартала 2019 года составил 2,1 %, также, как и в 3 квартале. Основными движущими силами данного роста были рост государственных расходов, расходов на личное потребление, инвестиции в основной капитал, государственные и местные правительственные расходы, которые были частично компенсированы отрицательными результатами капитальных нежилых инвестиций и частными инвестициями в товарно-материальные запасы. Импорт, который вычитается при расчете ВВП, снизился.

Регрессионный анализ

Для построения эконометрической модели темпов роста ВВП была выбрана модель множественной линейной регрессии. Оценка регрессии проводилась с помощью метода наименьших квадратов. Набор данных, взятых для анализа, охватывает период с первого квартала 2000 года по четвертый квартал 2019 года. Выбранные нами данные отражают рост за четыре предыдущих квартала.

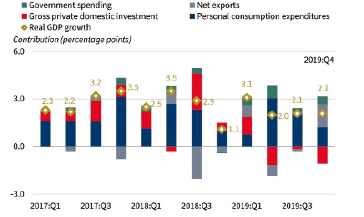
Рис. 1. Темпы роста реального ВВП США [16]

Экзогенной переменной является темп роста реального ВВП США – Yt. Нами были использованы следующие переменные в качестве эндогенных:

CGt – темп роста расходов на личное потребление товаров, %;

CSt – темп роста расходов на личное потребление услуг, %;

It – темп роста валовых частных внутренних инвестиций, %;

Ext – темп роста экспорта, %;

Imt – темп роста импорта, %;

Gt – темп роста государственных расходов на потребление и валовых инвестиций, %.

Далее согласно первому принципу спецификации модели необходимо перевести экономические законы в математический язык, в связи с чем использовались линейные математические уравнения для построения модели [1, 2]. Согласно второму принципу спецификации количество уравнений должно равняться количеству эндогенных переменных, в связи с чем дополнительные условия добавлены [3]. Таким образом, первоначальная форма модели была сформирована.

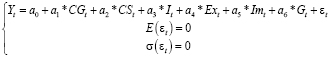(1)

Для выполнения третьего принципа спецификации – датирования всех переменных был введен индекс t в каждой эндогенной переменной [4, 5]. Также мы выполнили требование четвертого принципа спецификации – отражения случайного возмущения с помощью введения переменной ε_t.

Первым этапом конструирования нашей модели является проведение корреляционного анализа для определения взаимосвязи между экзогенным и эндогенными переменными [14, 15]. В результате анализа мы определили, что имеется сильная позитивная линейная взаимосвязь между темпом роста валовых частных внутренних инвестиций и темпом роста реального ВВП США, тогда как между темпом роста реального ВВП США и темпами роста расходов на личное потребление товаров, экспорта и импорта имеется заметная позитивная линейная взаимосвязь. Стоит отметить, что связь между темпом роста реального ВВП США и темпами роста расходов на личное потребление услуг является умеренной. Мы также определили, что связь между темпами роста государственных расходов на потребление и валовых инвестиций и темпами роста реального ВВП США отсутствует, несмотря на это данный показатель не исключен из нашего набора данных до проведения t-теста (табл. 1).

Поскольку определены связи между исследуемыми показателями и построена первоначальная модель, мы провели регрессионный анализ, результаты которого представлены в табл. 2. R2 составил 0,981, что свидетельствует о весьма высокой связи между экзогенными и эндогенными переменными, согласно шкале Чеддока [6, 7]. В целом, мы можем интерпретировать данный результат как соответствие модели данными, и что 98 % отклонения экзогенной переменной объясняется изменениями эндогенных переменных (табл. 2).

Используя результаты регрессионного анализа, первичная эконометрическая модель может быть преображена в оцененную форму [8]. Оцененная модель отражает взаимоотношения между экономическими показателями, ранее отраженными в качестве переменных. Правильное отражение оцененной модели предполагает написание результатов в форме системы уравнений:

1. Все коэффициенты a0, a1, a2, a3, a4, a5, a6 должны быть заменены значениями, полученными в ходе регрессионного анализа –0.245, 0.236, 0.509, 0.158, 0.118, –0.154, 0.185.

2. Стандартная ошибка должна быть написана под каждым коэффициентом в скобках [9].

3. Основные индикаторы достаточности модели также должны быть указаны, такие как R2, F наблюдаемая, F критическая со степенями свободы df1 and df2, tcrit со степенями свободы df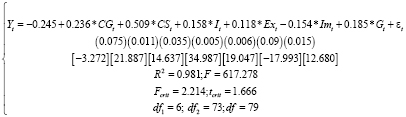2.

(2)

Таблица 1

Корреляционная матрица

Таблица 2

Регрессионный анализ

Проверка значимости рассчитанного уравнения проведена с помощью F-критерия Фишера. Наблюдаемое (рассчитанное) значение превышает критическое значение Фишера, что свидетельствует о невыполнении нулевой гипотезы Н0 о статической незначимости уравнения [10, 11]. Также невыполнение нулевой гипотезы предполагает, что значение коэффициента детерминации является не случайным и качество спецификации модели является высоким.

Проверка значимости рассчитанных коэффициентов уравнения проведена с помощью t- теста [12, 13]. В результате сопоставления критического значения t с рассчитанными значениями t было определенно, что по всем исследуемым коэффициентам нулевая гипотеза о незначимости коэффициентов отклонена, с вероятностью ошибки в 1 %, все рассчитанные коэффициенты являются значимыми, в связи с чем переменные данных коэффициентов не исключены (табл. 3).

Таблица 3

t-статистика

Для проверки математической адекватности нами рассчитаны верхний и нижний интервал возможного нахождения предсказанной с помощью модели величины в четвертом квартале 2019 года. Как можно заметить из таблицы 4 спрогнозированное значение роста ВВП составляет 2,2 % что на 1 базисный пункт выше реального значения, но все еще находится в доверительном интервале. Разница между верхним и нижним интервалами равняется 1,1, что не является значительной величиной и свидетельствует об адекватности модели.

Таблица 4

Тест на адекватность модели

Применение метода наименьших квадратов предполагает выполнение нескольких основополагающих предпосылок теоремы Гаусса Маркова [14]. Первой из которых является равенство математического ожидания случайных отклонений нулю для всех наблюдений. Для проверки выполнения данной предпосылки в MS Excel рассчитана средняя величина, которая равна нулю. Выполнение первой предпосылки доказывает, что случайное отклонение в выборке данных не имеет систематического смещения.

Следующим требованием применения МНК является постоянство дисперсии случайных отклонений для всех наблюдений. Для определения выполнения описанной предпосылки был проведен тест Голдфелда Квандта с уровнем значимости 5 %, результаты которого представлены в табл. 5.

Таблица 5

Тест Голдфелда Квандта

Согласно данным, представленным в таблице критическое значение Фишера, составляет 2,014, тогда как наблюдаемое значение равнялось 1,549, таким образом можно подытожить, что нулевая гипотеза Н0 принимается в модели имеет место гомоскедастичность.

Третье условие теоремы Гаусса-Маркова предполагает отсутствие автокорреляции – некоррелирование между собой случайных отклонений в выборке. Широко применимым методом определения автокорреляции является тест Дарбина Уотсона. Поскольку в исследуемой модели рассматривается 6 переменных в 80 периодах значения статистики, при 5 % уровне значимости, составляют следующие результаты dl = 1.480 и du = 1.801. Согласно расчётам в MS Excel значение статистики Дарбина-Уотсона равняется 2,067 и поскольку 4-du <DW <dl гипотеза об отсутствии автокорреляции подтверждается. Делается вывод об отсутствии автокорреляции в наблюдаемой выборке (рис. 2).

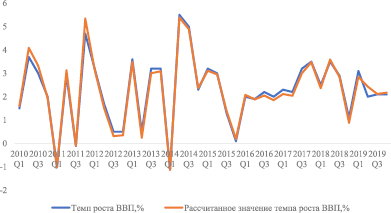
Рис. 2. Фактические и рассчитанные темпы роста ВВП США

После успешного выполнения необходимых тестов графики фактического и рассчитанного, по модели, темпов роста ВВП США были построены. Как можно заметить из рис. 2, модель достаточно хорошо описывает данные.

Заключение

Представленная эконометрическая модель построена согласно основным принципам эконометрики, а коэффициенты ее переменных значимы. В ходе выполнения работы модель успешно прошла необходимые тесты.

В ходе корреляционного анализа мы определили, что все исследованные переменные имеют линейную связь с темпом роста реального ВВП США за исключением такой переменной как темп роста государственных расходов на потребление и валовых инвестиций.

Коэффициент детерминации равняется 0,981, что свидетельствует о том, что 98 % отклонения экзогенной переменной объясняется изменениями эндогенных переменных. Выполнение F-теста доказало, что значение коэффициента детерминации является не случайным и качество спецификации модели является высоким.

Коэффициенты при переменных и постоянная величина были проверены на значимость путем использования t-теста. В результате теста было определено, что коэффициенты являются значимыми и не должны исключаться из модели.

Для применения МНК были выполнены предпосылки теоремы Гаусса Маркова. Мы определили, что математическое ожидание случайных отклонений для всех наблюдений равно нулю. Путем использования теста Голдфелда Квандта было определено, что дисперсии случайных отклонений постоянны для всех наблюдений. В ходе использования теста Дарбина Уотсона было определено, что отсутствует автокорреляция в наблюдаемой выборке.

В результате проведенного анализа можно подытожить, что оцененная модель может применяться для осуществления прогнозов при наличии информации о эндогенных переменных.