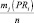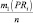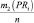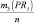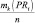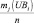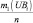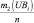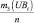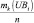Введение
Поставленные в настоящее время задачи ускорения экономического роста российской экономики обуславливают необходимость повышения эффективности управления на всех её уровнях. В этой связи одним из базовых направлений стратегического управления промышленными предприятиями, как основного звена экономики, является развитие инструментария анализа рисков, позволяющего адекватно реагировать на изменения воздействий внутренней и внешней среды. Существующее экономическое и политическое положение российской экономики диктует необходимость применения новых подходов к созданию инструментария риск-менеджмента, базирующегося на экономико-математическом моделировании и программной реализации его результатов с последующем проведением компьютерных экспериментов при оценке неблагоприятных ситуаций и вызванных ими последствий в виде потерь и убытков.
Цель исследования. Разработка и применение нового инструментария риск-менеджмента для оценки нестабильных условий функционирования современного предприятия.
Материал и методы исследования
В научных публикациях по проблемам анализа рисковых ситуаций представлен широкий спектр результатов исследований. Методологическим, организационным и технологическим аспектам риск-менеджмента посвящены исследования К.В. Балдина, С.Н. Воробьёва [1]. Авторами предложены методы системного анализа и математического моделирования при оценке рисковых ситуаций. Вопросы теории и практики риск-менеджмента на предприятии освещены в работе Е.Н. Станиславчик [2], Г.В. Черновой [3], Э.А. Уткина и Д.В. Фролова [4]. Вопросы инвестиционного менеджмента в условиях риска отражены в исследованиях Л.Г. Матвеевой, А.Ю. Никитаевой, О.А. Черновой, Е.Ф. Щипанова [5]. Проблемам разработки комплекса мер эффективного управления взаимодействия государства и бизнеса в условиях кризиса посвящены работы Т.В. Игнатовой [6, 7].
Результаты исследования и их обсуждение
Рассмотрение трудов в сфере исследований рисковых ситуаций и создания инструментария риск-менеджмента позволил декомпозировать подходы к разработке количественных методов анализа на два класса: детерминированные и стохастические методы. В данной статье авторами предложены экономико-математические модели для анализа рисковых ситуаций, функционирующие в условиях стохастической неопределённости. При этом уровень риска оценивается интегральным показателем «Коэффициент риска», вычисляемого как отношение
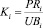
ожидаемой прибыли PRi к величине и ожидаемого убытка UBi при сравнении различных вариантов стратегических ориентиров, на которые нацелено предприятие. Коэффициент риска Ki показывает величину дохода, приходящегося на один рубль убытка. Концептуальная схема задачи риск-менеджмента с кибернетических позиций приведена на рис. 1.
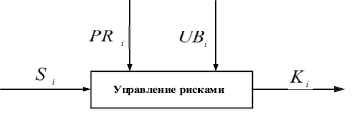
Рис. 1. Концептуальная схема риск-менеджмента
На схеме, представленной на рис. 1 входными управляемыми переменными являются варианты стратегических ориентиров Si,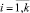 
предприятий. Величины прибыли PRi и убытков UBi при выборе стратегии Si изменяющиеся случайным образом и выступают в роли возмущений.
Выходными параметрами являются коэффициенты стратегического риска Ki при выборе стратегического ориентира Si. Задача риск-менеджмента состоит в выборе такого стратегического ориентира Si, при котором коэффициент риска Ki был бы оптимальным:
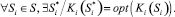
Стратегический ориентир развития промышленного предприятия определяет направление его развития, включая цели и методы их достижения в перспективе. Таким образом, стратегия управления риском должна быть согласована со стратегией внутрифирменного планирования промышленного предприятия. Стратегии завоевания рынка или поддержания сложившегося на рынке имиджа организации и сохранения финансовой устойчивости влекут за собой различные варианты стратегии риска. Авторами предложен комплекс экономико-математических моделей Ω = <ω1, ω2> для количественной оценки стратегического риска. Комплекс Ω включает в себя следующие компоненты:
ω1 – модели построения эмпирических законов распределений случайных величин PRi и UBi исходя из выборочных данных;
ω2 – имитационная модель оценки коэффициента стратегического риска.
Эмпирические законы распределения случайных величин PRi и UBi строятся на основе использования статистических данных, которые собраны в виде выборок
PRi = {zi1, zi2, ..., zin}, UBi = {ri1, ri2, ..., rin}
из генеральных совокупностей. В выборках переменные zij, rij означают величины ежедневных значений соответственно прибылей и убытков при выборе стратегического ориентира Si,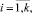 
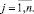Построение законов распределения осуществляется в следующей последовательности действий. Сначала определяются размахи варьирований величин PRi и UBi, как разности
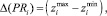
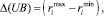
где 
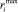– максимальные,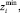 
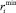– минимальные значения выборочных данных величин
PRi = {zi1, zi2, ..., zin}
и UBi = {ri1, ri2, ..., rin}:
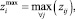
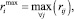
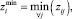
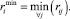
Размахи варьирований Δ(PRi) и Δ(UBi) делятся на k одинаковых отрезков dj(PRi) и dj(UBi), длина которых вычисляется в виде отношений
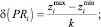
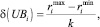
а координаты концов полученных отрезков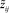 
и 
, 
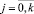определяются исходя из выражений (рис. 2):
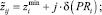
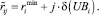
Затем вычисляются координаты середин полученных отрезков:
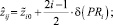
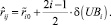
Эмпирические законы распределения случайных величин PRi и UBi представляют собой интервальные ряды распределения, приведённые в табл. 1 и 2. В первых строках табл. 1 и 2 приведены величины середин интервалов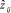 
и 
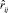, определяемые по ранее приведённым формулам. Вторые строки таблиц содержат относительные частоты попадания случайных величин PRi и UBi в заданные интервалы.
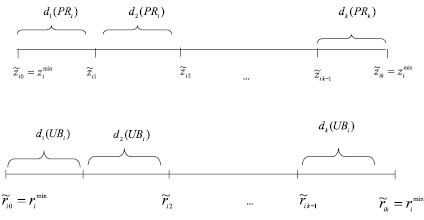
Рис. 2. Схема декомпозиции диапазонов изменений величин PRi и UBi на отрезки длиной соответственно δ(PRi) и δ(UBi)
Таблица 1
Эмпирический закон распределения случайной величины PRi
|
|
|
|
|
… |
|
|
|
|
|
|
… |
|
Таблица 2
Эмпирический закон распределения случайной величины UBi
|
|
|
|
|
… |
|
|
|
|
|
|
… |
|
В табл. 1 и 2 величины
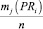и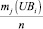 
, 
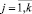
представляют собой относительные частоты попадания значений zij и rij случайных величин PRi и UBi в интервалы dl(PRi), dl(UBi),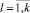 
, схематично представлены на рис. 2.
Построенные эмпирические законы распределения, формально описаны как отображения
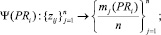
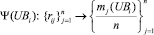
и используются в качестве исходных данных моделью ω2 для генерирования возможных значений случайных величин PRi и UBi. Генерация возможных значений случайных величин PRi и UBi осуществляется по методу статистических испытаний Монте-Карло на основе использования случайных чисел, равномерно распределённых на отрезке [0, 1]. Законы распределения вероятностей Ψ(PRi) и Ψ(UBi) участвуют в построении интервалов, длины которых соответствуют величинам относительных частот
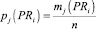
и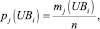 
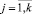(рис. 2).
Алгоритм функционирования модели ω2 приведён на рис. 3. Планируемый период исследования, в течение которого оценивается величина стратегического риска, задаётся в интерактивном режиме. В конце цикла определяется величина риска выбранного варианта стратегического ориентира по формуле
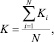
где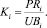 
Математические модели ω1 и ω2 получили программную реализацию в виде пакета прикладных программ «Risc-Menedger». Интерфейс программного средства представлен на рис. 4.
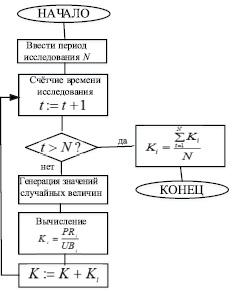
Рис. 3. Алгоритм функционирования имитационной модели ω2
Рис. 4. Интерфейс программного средства «Risc-Menedger»
Пункт «Ввод данных» выполняет ввод выборок из генеральных совокупностей, характеризующих случайные величины прибыли PRi и убытки UBi. По введённым выборочным данным строятся законы распределения случайных величин PRi и UBi, в соответствии с которыми генерируются по методу статистических испытаний прогнозируемые значения прибылей и убытков предприятия, а также определяются прогнозируемые значения коэффициентов риска.
На базе использования программного средства «Risc-Menedger» авторами продемонстрирована оценка стратегического риска при выборе варианта стратегического ориентира в условиях рисковых ситуаций. Исследования основаны на статистических данных о значениях случайных величин «Прибыли» PR и «Убытки» некоторого промышленного предприятия «ХХХ», приведенных табл. 3 за год, предшествующий планируемому.
С помощью комплекса программ «Risc-Menedger» для описания статистических данных, приведённых в табл. 3, построены эмпирические законы распределения вероятностей (рис. 5) и определены значения коэффициентов риска (рис. 6).
Построенные экономико-математические модели и основанные на них программные средства позволяют усовершенствовать механизм управления хозяйственными рисками в условиях неопределенности и нестабильности рыночного окружения.
Таблица 3
Статистические данные случайной величины PR и UB
|
Прибыль |
Убытки |
||||
|
175133 |
135687 |
142259 |
4769 |
8620 |
2239 |
|
214788 |
67845 |
157845 |
10467 |
324 |
157 |
|
98523 |
56783 |
117638 |
5680 |
769 |
7834 |
|
82678 |
125398 |
203465 |
2307 |
398 |
203 |
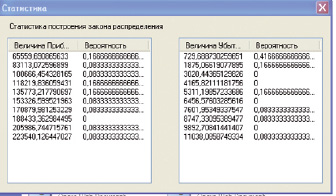
Рис. 5. Эмпирические законы распределения случайных величин PR и UB
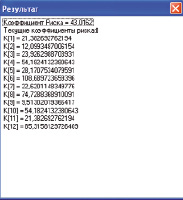
Рис. 6. Значения коэффициентов риска, полученные в программе «Risc-Menedger»
Выводы
В статье получены следующие научные результаты.
1. Предложен комплекс экономико-математических моделей, позволяющий давать количественную оценку стратегических рисков при выборе стратегических ориентиров развития промышленного предприятия на основе имитации процессов изменения текущих прибылей и убытков в условиях неопределённости.
2. Осуществлена программная реализация построенных экономико-математических моделей.
3. Произведены компьютерные эксперименты на созданном программном продукте с целью оценки стратегических ориентиров развития предприятия.