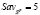Введение
Во многих задачах финансово-экономического содержания принятие решений зависит не только от субъекта, принимающего решение, но и от объективной действительности, о которой у субъекта, принимающего решение, в момент его принятия недостаточно информации. Часто подходящей математической моделью для анализа и решения таких задач служит «Игра с природой» (или в другой терминологии «Статистическая игра»), в которой участвуют два игрока: A – субъект, принимающий рациональные решения, П – природа, представляющая собой объективную действительность, окружающую данную задачу. Природа, не являющаяся ни противником, ни союзником игрока A, в любой момент принимает случайным образом то или иное состояние, не преследуя при этом конкретной цели и оставаясь абсолютно безразличной к результатам игры.
Для принятия решения, которое, как известно, является одной из главных составляющих любого управления, игрок A, будучи рациональным, стремится из возможных альтернативных стратегий выбрать стратегию, максимально отвечающую поставленным целям решения задачи. Для сравнения стратегий по их эффективности необходимо подобрать подходящий принцип оптимальности.
Проблема выбора принципа оптимальности стратегий в играх с природой – одна из центральных в теории принятия решений. Существуют разнообразные критерии оптимальности с различными свойствами. Некоторые из них, выигрыш-критерии, определяют оптимальность выбираемых стратегий с точки зрения выигрышей, абстрагируясь от рисков. Например, критерий Вальда [1; 2], максимаксный критерий [2] и др. Другие, риск-критерии, – наоборот, характеризуют оптимальность стратегий с позиций рисков, абстрагируясь от выигрышей. Например, критерий Сэвиджа [2, 3]; миниминный критерий [2] и др. Широко используются комбинированные критерии, составленные из двух выигрыш-критериев или двух риск-критериев. В каждой такой паре один из критериев является крайне пессимистическим, а другой – крайне оптимистическим. Например, классический выигрыш-критерий Гурвица [4, 5].
На наш взгляд заслуживает внимания также и подход выбора стратегии, оптимальной с синтетической (совместной) точки зрения выигрышей и игровых рисков. Такие критерии оптимальности будем называть синтетическими. В [2, 6, 7] предложен общий подход к конструированию синтетических критериев и приведены формулы показателей эффективности стратегий по различным синтетическим критериям. В работах [6, 8, 9] введен в рассмотрение синтетический критерий Вальда-Сэвиджа, проведен его детальный математический анализ и предложено приложение к решению задачи об установлении приоритетного порядка кредитования потенциальных корпоративных заемщиков банка.
Для описания критерия Вальда-Сэвиджа напомним кратко необходимые определения.
Критерий Вальда-Сэвиджа. Пусть в игре с природой игрок A обладает множеством 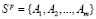 (В обозначении Sp буква "p" – первая буква английского pure – чистый. Она указывает на то, что рассматриваемые в данной статье стратегии А1, А2,…, Ат являются чистыми, а не смешанными, т.е. выбираются игроком A определенным образом без примесей случайности и неопределенности), m ≥ 2, альтернативных чистых стратегий, а П1, П2,…, Пn, n ≥ 2, – состояния природы П. Пусть действительные числа aij,
(В обозначении Sp буква "p" – первая буква английского pure – чистый. Она указывает на то, что рассматриваемые в данной статье стратегии А1, А2,…, Ат являются чистыми, а не смешанными, т.е. выбираются игроком A определенным образом без примесей случайности и неопределенности), m ≥ 2, альтернативных чистых стратегий, а П1, П2,…, Пn, n ≥ 2, – состояния природы П. Пусть действительные числа aij, 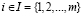 ,
, 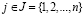 , – выигрыши игрока A в игровой ситуации (Ai, Пj), когда игрок A выбирает стратегию Ai, а природа находится в состоянии Пj. Величину
, – выигрыши игрока A в игровой ситуации (Ai, Пj), когда игрок A выбирает стратегию Ai, а природа находится в состоянии Пj. Величину 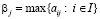 ,
, 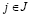 , назовем показателем благоприятности состояния Пj. Выбор игроком A стратегии Ai, когда природа находится в состоянии Пj, сопровождается риском
, назовем показателем благоприятности состояния Пj. Выбор игроком A стратегии Ai, когда природа находится в состоянии Пj, сопровождается риском 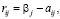
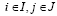 , не получения игроком A наибольшего при состоянии природы Пj выигрыша βj [2]. Таким образом, риск rij количественно характеризует упущенную игроком A возможность (при выборе им стратегии Ai) получения максимального выигрыша βj при нахождении природы в состоянии Пj и может интерпретироваться как своеобразная плата за отсутствие у игрока A информации о состоянии природы при выборе им стратегии Ai.
, не получения игроком A наибольшего при состоянии природы Пj выигрыша βj [2]. Таким образом, риск rij количественно характеризует упущенную игроком A возможность (при выборе им стратегии Ai) получения максимального выигрыша βj при нахождении природы в состоянии Пj и может интерпретироваться как своеобразная плата за отсутствие у игрока A информации о состоянии природы при выборе им стратегии Ai.
Критерий Вальда (W-критерий) описывается составляющими: 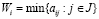 – показатель эффективности (W-показатель) стратегии Ai,
– показатель эффективности (W-показатель) стратегии Ai, 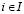 ;
; 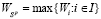 -цена (W-цена) игры в чистых стратегиях; Ak-стратегия, оптимальная (W-оптимальная) во множестве Sp чистых стратегий, если
-цена (W-цена) игры в чистых стратегиях; Ak-стратегия, оптимальная (W-оптимальная) во множестве Sp чистых стратегий, если 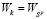 ;
; 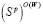 - множество стратегий, W-оптимальных во множестве Sp чистых стратегий.
- множество стратегий, W-оптимальных во множестве Sp чистых стратегий.
Критерий Сэвиджа (Sav-критерий) описывается составляющими: 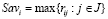 - показатель неэффективности (Sav-показатель) стратегии Ai,
- показатель неэффективности (Sav-показатель) стратегии Ai, 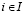 ;
; 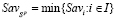 – цена (Sav-цена) игры в чистых стратегиях; Ak-стратегия, оптимальная (Sav-оптимальная) во множестве Sp чистых стратегий, если
– цена (Sav-цена) игры в чистых стратегиях; Ak-стратегия, оптимальная (Sav-оптимальная) во множестве Sp чистых стратегий, если 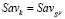 ;
; 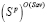 - множество стратегий, Sav-оптимальных во множестве Sp чистых стратегий.
- множество стратегий, Sav-оптимальных во множестве Sp чистых стратегий.
Далее нам понадобится критерий (–Sav), противоположный критерию Сэвиджа, который определяется следующим образом: 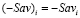 – показатель эффективности ((–Sav)-показатель) стратегии Ai,
– показатель эффективности ((–Sav)-показатель) стратегии Ai, 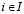 ;
; 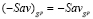 – цена ((–Sav)-цена) игры в чистых стратегиях; Ak-стратегия, оптимальная ((–Sav)-оптимальная) во множестве Sp чистых стратегий, если
– цена ((–Sav)-цена) игры в чистых стратегиях; Ak-стратегия, оптимальная ((–Sav)-оптимальная) во множестве Sp чистых стратегий, если 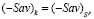 ;
; 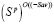 – множество стратегий, (–Sav)-оптимальных во множестве Sp чистых стратегий.
– множество стратегий, (–Sav)-оптимальных во множестве Sp чистых стратегий.
Два критерия будем называть эквивалентными во множестве чистых стратегий, если множества оптимальных чистых стратегий по этим критериям совпадают.
Предложение 1. Критерий Сэвиджа и противоположный ему критерий эквивалентны.
Доказательство. Пусть стратегия 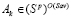 . Эта принадлежность по определению оптимальной стратегии эквивалентна равенству
. Эта принадлежность по определению оптимальной стратегии эквивалентна равенству 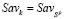 . Отсюда, по определениям (–Sav)-показателя и (–Sav)-цены игры получаем равенство (–Sav)k =
. Отсюда, по определениям (–Sav)-показателя и (–Sav)-цены игры получаем равенство (–Sav)k = 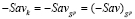 , которое означает, что
, которое означает, что 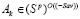 . Таким образом, доказано включение
. Таким образом, доказано включение
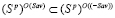 . (1)
. (1)
Докажем обратное включение. Пусть 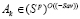 . Тогда
. Тогда 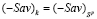 . Отсюда
. Отсюда 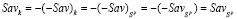 и, следовательно,
и, следовательно,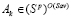 . Итак, доказано включение
. Итак, доказано включение
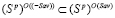 . (2)
. (2)
Из (1) и (2) следует равенство 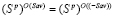 , означающее эквивалентность Sav-критерия и (–Sav)-критерия во множестве Sp.
, означающее эквивалентность Sav-критерия и (–Sav)-критерия во множестве Sp.
В определении критерия Вальда-Сэвиджа важную роль играют выигрыш-показатель 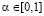 и риск-показатель
и риск-показатель 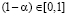 степени предпочтения, отдаваемого игроком A соответственно выигрышам и рискам. Выбор игроком A значения выигрыш-показателя
степени предпочтения, отдаваемого игроком A соответственно выигрышам и рискам. Выбор игроком A значения выигрыш-показателя 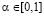 является субъективным и связан с его психологическими особенностями, определяющими его отношение к выигрышам и рискам.
является субъективным и связан с его психологическими особенностями, определяющими его отношение к выигрышам и рискам.
При α = 0 и, следовательно, 1 – α = 1, игрок A при выборе стратегии абстрагируется от выигрышей, сконцентрировав свое внимание только на рисках. И, наоборот, при α = 1 и, следовательно, 1 – α = 0, игрок A во главу угла ставит выигрыши, абстрагируясь от рисков.
Критерий Вальда-Сэвиджа с выигрыш-показателем 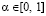 (
(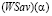 критерий), определяется составляющими:
критерий), определяется составляющими: 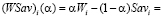
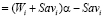 - показатель (
- показатель (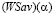 -показатель) эффективности стратегии Ai,
-показатель) эффективности стратегии Ai, 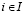 ;
; 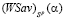
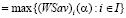 - цена (
- цена (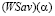 -цена) игры в чистых стратегиях; стратегию Ak назовем оптимальной (
-цена) игры в чистых стратегиях; стратегию Ak назовем оптимальной (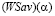 -оптимальной) во множестве Sp чистых стратегий, если
-оптимальной) во множестве Sp чистых стратегий, если 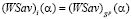 ;
; 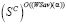 - множество стратегий,
- множество стратегий, 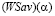 -оптимальных во множестве Sp чистых стратегий.
-оптимальных во множестве Sp чистых стратегий.
Очевидно, что при α = 0 критерий Вальда-Сэвиджа превращается в критерий, противоположный критерию Сэвиджа, и, следовательно, по предложению 1, эквивалентен критерию Сэвиджа. При α = 1 критерий Вальда-Сэвиджа превращается в критерий Вальда.
Из определения показателя 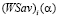 эффективности стратегии Ai видно, что он является линейной функцией аргумента
эффективности стратегии Ai видно, что он является линейной функцией аргумента 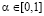 с угловым коэффициентом
с угловым коэффициентом 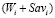 . Следовательно, графиком показателя
. Следовательно, графиком показателя 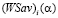 является отрезок
является отрезок 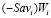 (обозначаемый двумя его концами) с левым концом
(обозначаемый двумя его концами) с левым концом 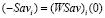 и правым концом
и правым концом 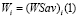 . Тогда графиком цены игры
. Тогда графиком цены игры 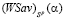 является, как следует из ее определения, верхняя огибающая m отрезков
является, как следует из ее определения, верхняя огибающая m отрезков 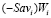 ,
, 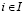 , и представляющая собой ломаную, состоящую из не более m звеньев, число которых обозначим через
, и представляющая собой ломаную, состоящую из не более m звеньев, число которых обозначим через 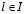 . Очевидно, что
. Очевидно, что 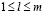 .
.
Проблема синтезирования оптимальных стратегий критерием Вальда-Сэвиджа
Определение 1. Стратегию, оптимальную по критерию Вальда-Сэвиджа при выигрыш-показателе 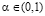 , будем называть синтезированной при данном выигрыш-показателе α, если она не является оптимальной ни по критерию Вальда, ни по критерию Сэвиджа,
, будем называть синтезированной при данном выигрыш-показателе α, если она не является оптимальной ни по критерию Вальда, ни по критерию Сэвиджа,
Определение 2. Будем говорить, что в данной игре критерий Вальда-Сэвиджа при фиксированном значении выигрыш-показателя 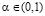 обладает свойством синтезирования, если при данном выигрыш-показателе α существует синтезированная стратегия, т.е.
обладает свойством синтезирования, если при данном выигрыш-показателе α существует синтезированная стратегия, т.е. 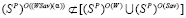 .
.
Определение 3. Если в данной игре ни при каком значении выигрыш-показателя 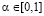 не существует синтезированной стратегии, т.е. при любом
не существует синтезированной стратегии, т.е. при любом 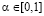 каждая стратегия, оптимальная по критерию Вальда-Сэвиджа, оптимальна либо по критерию Вальда, либо (связка «или» используется здесь в неразделительном смысле) по критерию Сэвиджа:
каждая стратегия, оптимальная по критерию Вальда-Сэвиджа, оптимальна либо по критерию Вальда, либо (связка «или» используется здесь в неразделительном смысле) по критерию Сэвиджа:
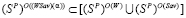 ,
,
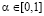 , (3)
, (3)
то будем говорить, что в этом случае критерий Вальда-Сэвиджа не обладает свойством синтезирования.
Понятно, что в общем случае не каждая стратегия, оптимальная или по критерию Вальда, или по критерию Сэвиджа, является оптимальной по критерию Вальда-Сэвиджа с некоторым выигрыш-показателем 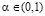 .
.
Так как при α = 0 и α = 1 критерий Вальда-Сэвиджа соответственно эквивалентен критерию Сэвиджа и совпадает с критерием Вальда, то при этих значениях выигрыш-показателя критерий Вальда-Сэвиджа свойством синтезирования не обладает. Именно поэтому в определениях 1 и 2 указанные значения выигрыш-показателя исключены из рассмотрения.
В следующем предложении сформулировано еще одно простое условие отсутствия у критерия Вальда-Сэвиджа свойства синтезирования.
Предложение 2. В игре, в которой число m чистых стратегий игрока A равно 2, критерий Вальда-Сэвиджа свойством синтезирования не обладает.
Доказательство. Пусть A1 и A2 – чистые стратегии игрока A. Графики показателей эффективности 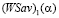 и
и 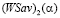 этих стратегий – отрезки
этих стратегий – отрезки 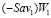 и
и 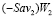 либо совпадают, либо не пересекаются, либо пересекаются.
либо совпадают, либо не пересекаются, либо пересекаются.
В первых двух случаях графиком цены игры 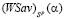 является отрезок. Тогда по необходимой части теоремы 11 из [10] в игре существует стратегия, оптимальная и по критерию Вальда, и по критерию Сэвиджа, т.е. выполняется условие
является отрезок. Тогда по необходимой части теоремы 11 из [10] в игре существует стратегия, оптимальная и по критерию Вальда, и по критерию Сэвиджа, т.е. выполняется условие
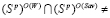 O. (4)
O. (4)
Из условия (4) по достаточной части теоремы 10 из [10] следует равенство 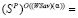
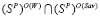 , при
, при 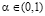 , из которого вытекает включение (3), означающее по определению 3, что
, из которого вытекает включение (3), означающее по определению 3, что 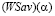 -критерий свойством синтезирования не обладает.
-критерий свойством синтезирования не обладает.
Если же отрезки 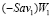 и
и 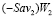 пересекаются, то очевидно, что выполняется включение (3), из которого по определению 3 также следует, что критерий Вальда-Сэвиджа свойством синтезирования не обладает.
пересекаются, то очевидно, что выполняется включение (3), из которого по определению 3 также следует, что критерий Вальда-Сэвиджа свойством синтезирования не обладает.
Таким образом, при α = 0 или α = 1, или m = 2 никакого синтезирования быть не может. Значит, ожидать синтезированное решение в результате применения критерия Вальда-Сэвиджа можно только при выигрыш-показателях 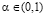 и при числе чистых стратегий m ≥ 3, что мы и будем предполагать в дальнейшем.
и при числе чистых стратегий m ≥ 3, что мы и будем предполагать в дальнейшем.
Из определения критерия Вальда-Сэвиджа [11, 12] следует, что его предназначение состоит в синтезировании крайне высоких предпочтений, отдаваемых лицом, принимающим решение, выигрышам (α = 1 и в этом случае им используется критерий Вальда) и рискам (α = 0 и в этом случае используется критерий Сэвиджа). В связи с этим возникает вопрос. В любой ли игре (при условиях 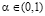 и m ≥3) критерий Вальда-Сэвиджа обладает свойством синтезирования?
и m ≥3) критерий Вальда-Сэвиджа обладает свойством синтезирования?
Таким образом, возникает проблема синтезирования критерием Вальда-Сэвиджа. В настоящей статье дано решение этой проблемы: найдены необходимые и достаточные условия игры с природой, для которой критерий Вальда-Сэвиджа свойством синтезирования не обладает, и, следовательно, применять его для отыскания синтезированных стратегий не имеет смысла [13, 14, 15]. Тем не менее, решение, полученное в результате применения критерия Вальда-Сэвиджа, выявляет зависимость стратегий, оптимальных или по критерию Вальда, или по критерию Сэвиджа от значений выигрыш-показателя 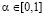 . Приложение полученных результатов иллюстрируется на примере задачи с экономическим содержанием.
. Приложение полученных результатов иллюстрируется на примере задачи с экономическим содержанием.
Решение проблемы синтезирования критерием Вальда-Сэвиджа. В доказательстве предложения 2 было показано, что при условии (4), т.е. при условии существования стратегии, оптимальной и по критерию Вальда и по критерию Сэвиджа, критерий Вальда-Сэвиджа свойством синтезирования не обладает. Поэтому в дальнейшем будем предполагать, что такой стратегии не существует, т.е.
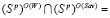 O. (5)
O. (5)
Условие (5) эквивалентно невыполнению условия (4), которое эквивалентно равенству l = 1. Следовательно, условие (5) эквивалентно тому, что l ≠ 1 или, что то же l ≥ 2. Таким образом, отсутствие в игре стратегии, оптимальной и по критерию Вальда, и по критерию Сэвиджа, эквивалентно тому, что ломаная, представляющая график цены игры 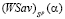 , состоит из не менее двух звеньев: l ≥ 2.
, состоит из не менее двух звеньев: l ≥ 2.
Если каждая чистая стратегия оптимальна по критерию Вальда или по критерию Cэвиджа: 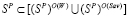 , то критерий Вальда-Сэвиджа не обладает свойством синтезирования. Поэтому далее будем считать, что существуют стратегии, не являющиеся оптимальными ни по критерию Вальда, ни по критерию Сэвиджа:
, то критерий Вальда-Сэвиджа не обладает свойством синтезирования. Поэтому далее будем считать, что существуют стратегии, не являющиеся оптимальными ни по критерию Вальда, ни по критерию Сэвиджа:
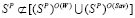 . (6)
. (6)
Пусть 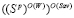 – множество стратегий, оптимальных по критерию Сэвиджа во множестве
– множество стратегий, оптимальных по критерию Сэвиджа во множестве 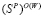 стратегий, оптимальных по критерию Вальда, и
стратегий, оптимальных по критерию Вальда, и 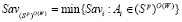 – цена игры по критерию Сэвиджа в стратегиях множества
– цена игры по критерию Сэвиджа в стратегиях множества 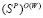 ;
; 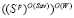 – множество стратегий, оптимальных по критерию Вальда во множестве
– множество стратегий, оптимальных по критерию Вальда во множестве 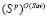 стратегий, оптимальных по критерию Сэвиджа, и
стратегий, оптимальных по критерию Сэвиджа, и 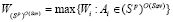 – цена игры по критерию Вальда в стратегиях множества
– цена игры по критерию Вальда в стратегиях множества 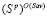 .
.
Нетрудно видеть, что множества 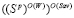 и
и 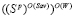 не пусты и справедливы включения
не пусты и справедливы включения 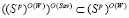 и
и 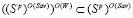 .
.
Графики показателей эффективности 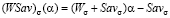 всех стратегий
всех стратегий 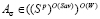 совпадают и представляют собой отрезок с левым концом
совпадают и представляют собой отрезок с левым концом 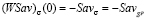 и правым концом
и правым концом 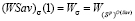 , т.е. отрезок
, т.е. отрезок 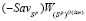 (см. рис. 1).
(см. рис. 1).
Аналогично, графики показателей эффективности 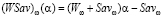 всех стратегий
всех стратегий 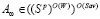 совпадают и представляют собой отрезок с левым концом
совпадают и представляют собой отрезок с левым концом 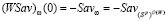 и правым концом
и правым концом 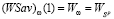 , т.е. отрезок
, т.е. отрезок 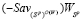 (см. рис. 1).
(см. рис. 1).
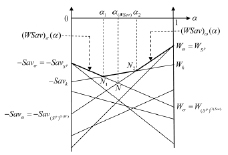
Рис. 1. Графики показателей эффективности стратегий в случае, когда ломаная, представляющая график цены игры по критерию Вальда-Сэвиджа, состоит из трех звеньев (l = 3)
Определение 4. В предположении выполнения условия (6), будем говорить, что игра удовлетворяет условию 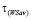 , если для каждой чистой стратегии Ak, не являющейся оптимальной ни по критерию Вальда, ни по критерию Сэвиджа (существующей в силу условия (6)), т.е. для которой выполняется условие
, если для каждой чистой стратегии Ak, не являющейся оптимальной ни по критерию Вальда, ни по критерию Сэвиджа (существующей в силу условия (6)), т.е. для которой выполняется условие
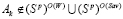 , (7)
, (7)
справедливо неравенство
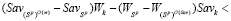
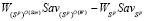 . (8)
. (8)
Отметим, что для стратегии 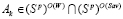 неравенство (8) не выполняется, поскольку в этом случае
неравенство (8) не выполняется, поскольку в этом случае 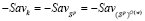 и
и 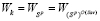 , и, следовательно, левая и правая части неравенства (8) превращаются в нули.
, и, следовательно, левая и правая части неравенства (8) превращаются в нули.
Далее нам понадобится следующее предложение, доказанное в [10, лемма 3].
Предложение 3. Пусть выполняется условие (5) и пусть 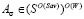 и
и 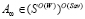 . Тогда отрезки
. Тогда отрезки 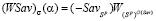 и
и 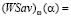 =
= 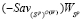 не совпадают и пересекаются в точке
не совпадают и пересекаются в точке 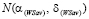 с абсциссой
с абсциссой
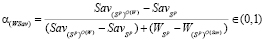 , (9)
, (9)
и ординатой
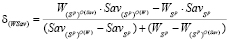 (10)
(10)
(см. рис. 1).
Необходимые условия отсутствия у критерия Вальда-Сэвиджа свойства синтезирования даны в следующей теореме.
Теорема 1 (необходимые условия отсутствия синтезирования). Пусть в игре не существует стратегии, оптимальной одновременно по критерию Вальда и по критерию Сэвиджа, т.е. выполняется условие (5), и существует стратегия, не являющаяся оптимальной ни по критерию Вальда, ни по критерию Сэвиджа, т.е. выполняется условие (6).
Тогда если в данной игре критерий Вальда-Сэвиджа не обладает свойством синтезирования, то справедливы следующие утверждения:
а) число l звеньев ломаной, представляющей график цены игры по критерию Вальда-Сэвиджа 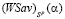 , равно 2;
, равно 2;
b) игра удовлетворяет условию 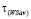 ;
;
c) множество 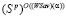 стратегий, оптимальных по критерию Вальда-Сэвиджа, имеет следующую структуру
стратегий, оптимальных по критерию Вальда-Сэвиджа, имеет следующую структуру
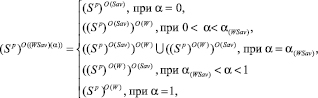 (11)
(11)
где 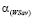 определяется формулой (9).
определяется формулой (9).
Доказательство. Докажем утверждение a). Как было показано выше, условие (5) эквивалентно тому, что l ≥ 2. Предположим противное утверждению a): l ≠ 2. Тогда l ≥ 3.
В этом случае найдется стратегия Ak, такая, что отрезок 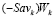 , являющийся графиком показателя эффективности
, являющийся графиком показателя эффективности 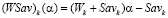 , будет пересекать отрезок
, будет пересекать отрезок 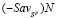 во внутренней его точке N1, порождая звено N1N2 ломаной
во внутренней его точке N1, порождая звено N1N2 ломаной 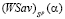 (см. рис. 1). Отрезок
(см. рис. 1). Отрезок 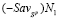 является первым (слева направо) звеном ломаной
является первым (слева направо) звеном ломаной 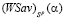 . Точка N2 является концом второго звена и началом третьего звена (На рис. 1 приведен случай l = 3; ломаная
. Точка N2 является концом второго звена и началом третьего звена (На рис. 1 приведен случай l = 3; ломаная 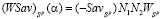 , выделенная жирной линией, состоит из трех звеньев
, выделенная жирной линией, состоит из трех звеньев 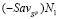 ,
, 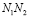 и
и 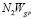 ).
).
По определению Sav-цены игры, 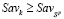 . Но
. Но 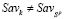 , поскольку в противном случае было бы справедливо равенство
, поскольку в противном случае было бы справедливо равенство 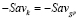 и тогда отрезок
и тогда отрезок 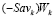 не мог бы пересечь отрезок
не мог бы пересечь отрезок 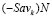 во внутренней его точке N1. Таким образом, имеет место неравенство
во внутренней его точке N1. Таким образом, имеет место неравенство 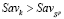 , означающее, что стратегия Ak не является Sav-оптимальной:
, означающее, что стратегия Ak не является Sav-оптимальной:
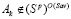 . (12)
. (12)
Справедливо неравенство
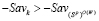 , (13)
, (13)
поскольку в противном случае: 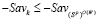 и тогда отрезок
и тогда отрезок 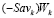 не мог бы пересекать отрезок
не мог бы пересекать отрезок 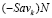 во внутренней его точке N1 (см. рис. 1).
во внутренней его точке N1 (см. рис. 1).
По определению W-цены игры  . Но
. Но 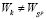 , поскольку в противном случае стратегия
, поскольку в противном случае стратегия 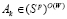 и по определению цены игры в стратегиях множества
и по определению цены игры в стратегиях множества 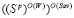 по критерию Сэвиджа
по критерию Сэвиджа 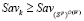 , откуда следует неравенство
, откуда следует неравенство 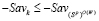 , противоречащее неравенству (13). Таким образом,
, противоречащее неравенству (13). Таким образом, 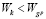 и, следовательно, стратегия Ak не является W-оптимальной:
и, следовательно, стратегия Ak не является W-оптимальной:
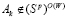 . (14)
. (14)
Пусть α1 и α2 – абсциссы соответственно левого и правого концов второго звена ломаной 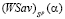 (см. рис. 1). Тогда при каждом значении выигрыш-показателя
(см. рис. 1). Тогда при каждом значении выигрыш-показателя 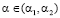 критерий Вальда-Сэвиджа будет обладать свойством синтезирования, так как при каждом
критерий Вальда-Сэвиджа будет обладать свойством синтезирования, так как при каждом 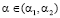 , будем иметь
, будем иметь 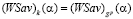 , т.е. стратегия Ak является
, т.е. стратегия Ak является 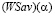 -оптимальной, но не является оптимальной ни по критерию Вальда (см. (14)), ни по критерию Сэвиджа (см. (12)). Но это противоречит условию теоремы.
-оптимальной, но не является оптимальной ни по критерию Вальда (см. (14)), ни по критерию Сэвиджа (см. (12)). Но это противоречит условию теоремы.
Полученное противоречие доказывает, что l = 2. Утверждение a) доказано.
Докажем утверждение b). По доказанному утверждению a) число звеньев ломаной 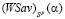 равно 2 (l = 2). Символический вид этой ломаной изображен на рис. 2 (выделена жирной линией).
равно 2 (l = 2). Символический вид этой ломаной изображен на рис. 2 (выделена жирной линией).
Пусть Ak – произвольная чистая стратегия, не являющаяся оптимальной ни по критерию Вальда, ни по критерию Сэвиджа, т.е. удовлетворяющая условию (7) (существование таких стратегий обусловлено требованием (6)). Графиком показателя эффективности этой стратегии по критерию Вальда-Сэвиджа 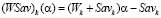 является отрезок
является отрезок 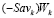 (обозначаемый его концами).
(обозначаемый его концами).
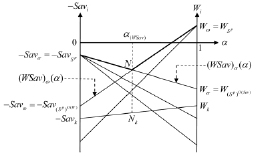
Рис. 2. Графики показателей эффективности стратегий в случае, когда ломаная, представляющая график цены игры по критерию Вальда-Сэвиджа, состоит из двух звеньев (l = 2)
Докажем, что значение 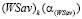 показателя эффективности
показателя эффективности 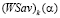 стратегии Ak при выигрыш-показателе
стратегии Ak при выигрыш-показателе 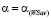 меньше, чем ордината
меньше, чем ордината 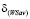 точки N:
точки N:
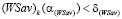 (15)
(15)
(на рис. 2 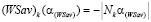 , где
, где 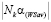 – длина отрезка
– длина отрезка 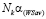 ).
).
Левый конец 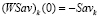 этого отрезка не может равняться
этого отрезка не может равняться 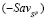 :
:
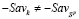 , (16)
, (16)
поскольку в противном случае стратегия 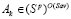 , что противоречит условию (7). Аналогично, правый конец
, что противоречит условию (7). Аналогично, правый конец 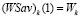 отрезка
отрезка 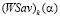 не может совпадать с
не может совпадать с 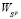 :
:
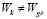 . (17)
. (17)
ибо в противном случае 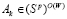 , что также противоречит (7).
, что также противоречит (7).
Левый конец 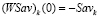 отрезка
отрезка 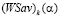 , в силу определения
, в силу определения 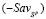 , не может быть больше
, не может быть больше 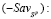
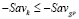 , (18)
, (18)
а правый конец 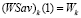 этого отрезка, в силу определению
этого отрезка, в силу определению 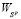 , не может быть больше
, не может быть больше 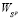 :
:
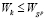 . (19)
. (19)
Из неравенств (16), (17), (18) и (19) следует, что отрезок 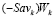 не может пересекать только один из отрезков
не может пересекать только один из отрезков 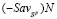 или
или 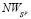 .
.
Отрезок 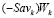 не может пересекать оба отрезка
не может пересекать оба отрезка 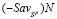 и
и  , ибо в противном случае ломаная
, ибо в противном случае ломаная 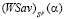 имела бы 3 звена, что противоречит утверждению a).
имела бы 3 звена, что противоречит утверждению a).
Отрезок 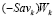 не может иметь с отрезками
не может иметь с отрезками 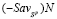 и
и 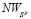 единственную общую точку N. В самом деле, если отрезок
единственную общую точку N. В самом деле, если отрезок 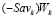 проходит через точку N и не имеет других общих точек ни с отрезком
проходит через точку N и не имеет других общих точек ни с отрезком 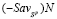 , ни с отрезком
, ни с отрезком 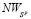 , то
, то 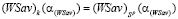 , т.е.
, т.е. 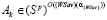 . Таким образом, стратегия Ak оптимальна во множестве чистых стратегий по критерию Вальда-Сэвиджа при выигрыш-показателе
. Таким образом, стратегия Ak оптимальна во множестве чистых стратегий по критерию Вальда-Сэвиджа при выигрыш-показателе 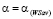 и не оптимальна ни по критерию Вальда, ни по критерию Сэвиджа. А это означает, что критерий Вальда Сэвиджа при выигрыш-показателе
и не оптимальна ни по критерию Вальда, ни по критерию Сэвиджа. А это означает, что критерий Вальда Сэвиджа при выигрыш-показателе 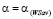 обладает свойством синтезирования, что противоречит условию теоремы.
обладает свойством синтезирования, что противоречит условию теоремы.
Итак, мы показали, что отрезок 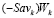 лежит ниже точки N. Этим доказано неравенство (15).
лежит ниже точки N. Этим доказано неравенство (15).
Левую часть неравенства (15) заменим по ее определению, а вместо выигрыш-показателя 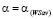 и ординаты
и ординаты 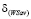 подставим их значения соответственно по формулам (9) и (10); в результате получим:
подставим их значения соответственно по формулам (9) и (10); в результате получим:
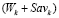
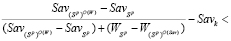
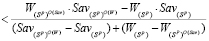 . (20)
. (20)
Из того, что 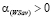 (см. (9)) и
(см. (9)) и 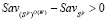 следует, что
следует, что 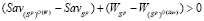 . Поэтому обе части неравенства (20) можем умножить на этот знаменатель, после чего элементарными преобразованиями получаем неравенство (8).
. Поэтому обе части неравенства (20) можем умножить на этот знаменатель, после чего элементарными преобразованиями получаем неравенство (8).
Таким образом, мы показали, что для любой стратегии, не являющейся оптимальной ни по критерию Вальда, ни по критерию Сэвиджа, справедливо неравенство (8), т.е. игра удовлетворяет условию 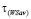 . Утверждение b) доказано.
. Утверждение b) доказано.
Для доказательства утверждения c) отметим, что оно, как было доказано в [10], следует из утверждения b).
Таким образом, теорема доказана.
Теорема 2 (достаточные условия отсутствия синтезирования). Пусть в игре не существует стратегии, оптимальной одновременно по критерию Вальда и по критерию Сэвиджа, т.е. выполняется условие (6), и существует стратегия, не являющаяся оптимальной ни по критерию Вальда, ни по критерию Сэвиджа, т.е. выполняется условие (7). Тогда из каждого из следующих условий следует, что критерий Вальда-Сэвиджа не обладает свойством сглаживания:
a) игра удовлетворяет условию 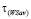 ;
;
b) множество 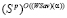 стратегий, оптимальных по критерию Вальда-Сэвиджа, имеет структуру (11).
стратегий, оптимальных по критерию Вальда-Сэвиджа, имеет структуру (11).
Доказательство. Докажем, что из условия a) следует утверждение теоремы.
Допустим противное утверждению теоремы, т.е. допустим, что существуют значение выигрыш-показателя 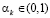 и стратегия Ak, удовлетворяющая условию (7) (такие стратегии существуют в силу условия (6)), которая является
и стратегия Ak, удовлетворяющая условию (7) (такие стратегии существуют в силу условия (6)), которая является 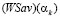 -оптимальной:
-оптимальной:
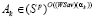 . (21)
. (21)
Из принадлежности (21), по определению оптимальности стратегии, следует равенство 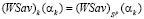 , означающее, что при α = αk отрезок, представляющий график показателя эффективности
, означающее, что при α = αk отрезок, представляющий график показателя эффективности 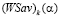 стратегии Ak, имеет общую точку с ломаной, представляющей график цены игры
стратегии Ak, имеет общую точку с ломаной, представляющей график цены игры 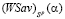 по критерию Вальда-Сэвиджа.
по критерию Вальда-Сэвиджа.
В силу условия (5) количество звеньев ломаной 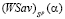 не меньше 2 (l ≥ 2) и, следовательно, отрезки
не меньше 2 (l ≥ 2) и, следовательно, отрезки 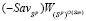 и
и 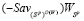 не совпадают и пересекаются в точке N (см. рис. 3, на котором число звеньев l = 4). В силу условия (7), отрезок
не совпадают и пересекаются в точке N (см. рис. 3, на котором число звеньев l = 4). В силу условия (7), отрезок 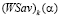 не может совпадать ни с одним из отрезков
не может совпадать ни с одним из отрезков 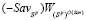 и
и 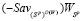 и также не может пересекать только один из отрезков
и также не может пересекать только один из отрезков 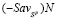 или
или 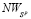 , поскольку из (7) следует, что
, поскольку из (7) следует, что 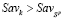 и потому
и потому 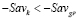 , а также
, а также 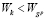 (см. рис. 3).
(см. рис. 3).
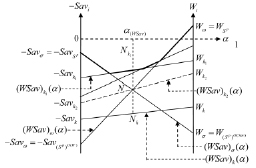
Рис. 3. Графики показателей эффективности оптимальных стратегий по критерию Вальда-Сэвиджа в случае, когда ломаная, представляющая график цены игры, состоит из четырёх звеньев (l = 4)
Если отрезок 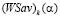 пересекает оба отрезка
пересекает оба отрезка 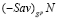 и
и 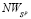 и занимает, например, положение отрезка
и занимает, например, положение отрезка 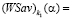
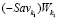 (см. рис. 3), то
(см. рис. 3), то
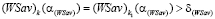 , (22)
, (22)
где 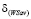 – ордината точки N (на рис. 3,
– ордината точки N (на рис. 3, 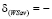
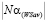 , где
, где 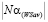 - длина отрезка
- длина отрезка 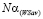 .
.
Если отрезок 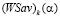 имеет с отрезками
имеет с отрезками 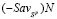 и
и 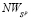 единственную общую точку N и занимает, например, положение отрезка
единственную общую точку N и занимает, например, положение отрезка 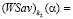
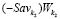 (см. рис. 3), то
(см. рис. 3), то
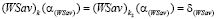 . (23)
. (23)
Оба случая (22) и (23) можно объединить одним неравенством 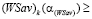
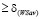 . Подставляя в это неравенство выражения для
. Подставляя в это неравенство выражения для 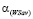 и
и 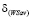 по формулам соответственно (9) и (10), получим
по формулам соответственно (9) и (10), получим
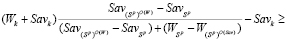
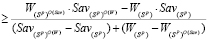 . (24)
. (24)
При доказательстве утверждения b) теоремы 1 была доказана положительность знаменателя в неравенстве (24). Умножая обе части этого неравенства на знаменатель и проведя элементарные преобразования, получим неравенство
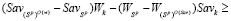
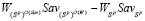 ,
,
которое противоречит неравенству (8). Следовательно, отрезок 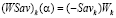 не имеет общих точек с ломаной, являющейся графиком цены игры, и потому стратегия Ak не является оптимальной по критерию Вальда-Сэвиджа. Таким образом, критерий Вальда-Сэвиджа не обладает свойством синтезирования.
не имеет общих точек с ломаной, являющейся графиком цены игры, и потому стратегия Ak не является оптимальной по критерию Вальда-Сэвиджа. Таким образом, критерий Вальда-Сэвиджа не обладает свойством синтезирования.
Итак, доказано, что из условия a) следует утверждение теоремы.
Теперь докажем, что утверждение теоремы следует также и из условия b). Пусть множество оптимальных стратегий по критерию Вальда-Сэвиджа имеет структуру (11) и пусть Ak – произвольная стратегия, оптимальная по критерию Вальда-Сэвиджа при некотором значении выигрыш-показателя 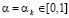 :
: 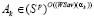 .
.
Из структуры (11) очевидным образом вытекают следующие утверждения: если 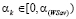 , то
, то 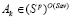 ; если
; если 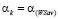 , то
, то 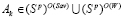 ; если
; если 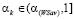 , то
, то 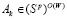 . Таким образом, справедливо включение
. Таким образом, справедливо включение 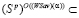
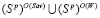 , означающее отсутствие у критерия Вальда-Сэвиджа свойства синтезирования. Теорема доказана.
, означающее отсутствие у критерия Вальда-Сэвиджа свойства синтезирования. Теорема доказана.
Из теорем 1 и 2 следует, что каждое из утверждений a) и b) теоремы 2 является необходимым и достаточным условием того, что критерий Вальда-Сэвиджа не обладает свойством синтезирования.
Условие a) теоремы 1, являясь необходимым условием отсутствия у критерия Вальда-Сэвиджа свойства синтезирования, не является достаточным. Для доказательства этого приведем следующий пример.
Пример 1. Пусть игра с природой задается матрицей А размера 3×2, в последней добавленной строке которой проставлены показатели благоприятности состояний природы 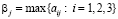 , j = 1, 2, а в последнем добавленном столбце – W-показатели стратегий и W-цена игры. По матрице А высчитываем риски
, j = 1, 2, а в последнем добавленном столбце – W-показатели стратегий и W-цена игры. По матрице А высчитываем риски 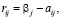 i = 1, 2, 3; j = 1, 2, и формируем матрицу рисков R, в последнем добавленном столбце которой стоят Sav-показатели стратегий и Sav-цена игры.
i = 1, 2, 3; j = 1, 2, и формируем матрицу рисков R, в последнем добавленном столбце которой стоят Sav-показатели стратегий и Sav-цена игры.
|
А = |
Пj Ai |
П1 |
П2 |
Wi |
|
A1 |
3 |
4 |
3 |
|
|
A2 |
10 |
–1 |
–1 |
|
|
A3 |
4 |
1 |
1 |
|
|
|
βj |
10 |
4 |
|
|
R = |
Пj Ai |
П1 |
П2 |
Savi |
|
A1 |
7 |
0 |
7 |
|
|
A2 |
0 |
5 |
5 |
|
|
A3 |
6 |
3 |
6 |
|
|
|
|
|||
На рис. 4 представлены отрезки 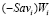 , i = 1, 2, 3, являющиеся графиками показателей эффективности
, i = 1, 2, 3, являющиеся графиками показателей эффективности 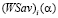 стратегий Ai. Отрезки
стратегий Ai. Отрезки 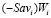 , i = 1, 2, пересекаются в точке
, i = 1, 2, пересекаются в точке 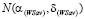 с абсциссой
с абсциссой 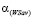 и ординатой
и ординатой 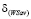 , образуя ломаную
, образуя ломаную 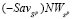 (выделенную на рис. 4 жирной линией), представляющую график цены игры
(выделенную на рис. 4 жирной линией), представляющую график цены игры 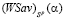 по критерию Вальда-Сэвиджа и состоящую из двух звеньев
по критерию Вальда-Сэвиджа и состоящую из двух звеньев 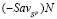 и
и 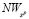 (l = 2).
(l = 2).
Абсцисса 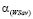 и ордината
и ордината 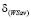 вычисляются соответственно по формулам (9) и (10).Очевидно, что
вычисляются соответственно по формулам (9) и (10).Очевидно, что 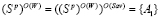 ;
; 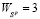 ;
; 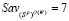 ;
; 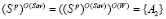 ;
; 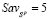 ;
; 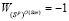 . Тогда по формулам (9) и (10) будем иметь:
. Тогда по формулам (9) и (10) будем иметь: 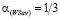 ,
, 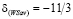 .
.
Стратегия A3 не является оптимальной ни по критерию Вальда, ни по критерию Сэвиджа, т.е. она удовлетворяет условию (10), поскольку (как явствует из последних дополнительных столбцов матриц A и R) 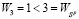 и
и 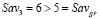 (на рис. 4 левый конец (
(на рис. 4 левый конец (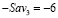 ) отрезка
) отрезка 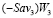 лежит ниже
лежит ниже 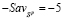 , а правый конец W3 = 1 отрезка
, а правый конец W3 = 1 отрезка 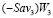 – ниже
– ниже 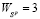 ).
).
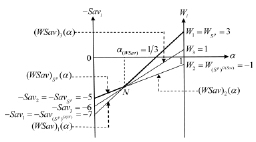
Рис. 4. Геометрическая интерпретация примера
Показатель эффективности стратегии A3 при выигрыш-показателе 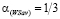 равен
равен 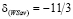 . В самом деле,
. В самом деле,
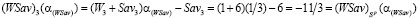 .
.
Таким образом, стратегия A3, не являющаяся оптимальной ни по критерию Вальда, ни по критерию Сэвиджа, оптимальна по синтетическому критерию Вальда-Сэвиджа при выигрыш-показателе 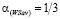 и, следовательно, критерий Вальда-Сэвиджа в данной игре обладает свойством синтезирования
и, следовательно, критерий Вальда-Сэвиджа в данной игре обладает свойством синтезирования
Итак, в данной игре ломаная, представляющая график цены игры, состоит из двух звеньев, но, тем не менее, критерий Вальда-Сэвиджа обладает свойством синтезирования.
Иллюстрация применения полученных результатов. Применение полученных результатов проиллюстрируем на решении следующей задачи оптимального планирования производства.
Постановка задачи. Для изготовления X единиц определенной продукции должен быть выбран один из четырех возможных технологических способов. Потребность в этой продукции носит случайный характер и, как показывает прошлый опыт, может принимать значения 25, 35, 45 или 50 единиц. Производственные затраты TCi на изготовление X единиц продукции i-м (i = 1, 2, 3, 4) технологическим способом включают постоянные затраты, соответственно: Q1 = 145, Q2 = 70, Q3 = 180, Q4 = 110 условных денежных единиц (у.д.е) и удельные переменные затраты, соответственно: c1 = 3, c2 = 5, c3 = 2, c4 = 4 условных денежных единиц (у.д.е). Общие затраты на производство продукции объемом Х по i-му технологическому способу выражаются формулой:
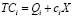 , i = 1, 2, 3, 4. (25)
, i = 1, 2, 3, 4. (25)
Ставится задача выбора одного из четырех технологических способов изготовления продукции с критерием на минимум производственных затрат.
Решение. Для анализа задачи адекватной является модель «Игры с природой», в которой рациональным игроком A выступает предприятие, а природой выступает потребность в изготавливаемой продукции. Игрок A располагает четырьмя чистыми стратегиями Ai, i = 1, 2, 3, 4 – выбрать для изготовления продукции i-й технологический способ, а «природа» может находится в одном из четырех состояниях: П1 = 25, П2 = 35, П3 = 45 и П5 = 50 единиц потребляемой продукции. В модели в качестве выигрышей aij (i, j = 1, 2, 3, 4) игрока A в игровой ситуации (Ai, Пj): игрок A выбирает стратегию Ai, а природа находится в состоянии Пj, будем рассматривать производственные затраты предприятия, вычисляемые по формуле (25). Таким образом, выигрыши aij (i, j = 1, 2, 3, 4), представляют собой отрицательные величины, которые в обозначениях модели рассчитываются по формуле: 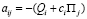 (i, j = 1, 2, 3, 4). На основе рассчитанных выигрышей aij формируем платежную матрицу А. Рассчитываем показатели
(i, j = 1, 2, 3, 4). На основе рассчитанных выигрышей aij формируем платежную матрицу А. Рассчитываем показатели 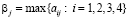 (j = 1, 2, 3, 4) благоприятности состояний природы и проставляем их в последней дополнительной строке матрицы А. Подсчитываем риски
(j = 1, 2, 3, 4) благоприятности состояний природы и проставляем их в последней дополнительной строке матрицы А. Подсчитываем риски 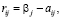 (i, j = 1, 2, 3, 4) и формируем матрицу рисков R.
(i, j = 1, 2, 3, 4) и формируем матрицу рисков R.
|
А = |
Пj Ai |
П1 |
П2 |
П3 |
П4 |
Wi |
|
A1 |
-220 |
-250 |
-280 |
-295 |
-295 |
|
|
A2 |
-195 |
-245 |
-290 |
-320 |
-320 |
|
|
A3 |
-230 |
-250 |
-270 |
-280 |
-280 |
|
|
A4 |
-210 |
-250 |
-290 |
-310 |
-310 |
|
|
|
βj |
-195 |
-245 |
-270 |
-280 |
|
R = |
Пj Ai |
П1 |
П2 |
П3 |
П4 |
Savi |
|
A1 |
25 |
5 |
10 |
15 |
25 |
|
|
A2 |
0 |
0 |
20 |
40 |
40 |
|
|
A3 |
35 |
5 |
0 |
0 |
35 |
|
|
A4 |
15 |
5 |
20 |
30 |
30 |
В последних добавленных столбцах матриц А и R проставлены W- и Sav-показатели стратегий. Перед тем как приступить к процедуре нахождения синтезированных стратегий целесообразно выяснить их существование. Для этого используем условие 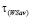 . Из показателей столбцов «Wi» и «Savi» матриц А и R следует, что
. Из показателей столбцов «Wi» и «Savi» матриц А и R следует, что
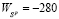 ,
, 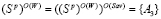 ,
, 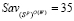 ,
,
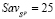 ,
, 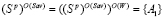 ,
, 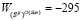 .
.
Тогда правая часть неравенства (8)
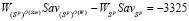 . (26)
. (26)
Так как стратегии A2 и A4 не принадлежат множеству 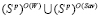 , то левую часть неравенства (8) надо подсчитать только для этих стратегий. Имеем:
, то левую часть неравенства (8) надо подсчитать только для этих стратегий. Имеем:
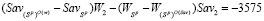 , (27)
, (27)
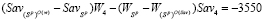 . (28)
. (28)
Из неравенств (26), (27) и (28) заключаем, что для стратегий A2 и A4 справедливо неравенство (8), т.е. данная игра удовлетворяет условию 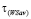 . Нетрудно видеть, что выполняются также условия (6) и (7). Таким образом, выполняются условия теоремы 2, в соответствии с которой критерий Вальда-Сэвиджа не обладает свойством синтезирования, т.е. применение критерия Вальда-Сэвиджа ни при каком значении выигрыш-показателя
. Нетрудно видеть, что выполняются также условия (6) и (7). Таким образом, выполняются условия теоремы 2, в соответствии с которой критерий Вальда-Сэвиджа не обладает свойством синтезирования, т.е. применение критерия Вальда-Сэвиджа ни при каком значении выигрыш-показателя 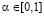 не приводит к синтезированным решениям и каждая стратегия, оптимальная по критерию Вальда-Сэвиджа, оптимальна либо по критерию Вальда, либо по критерию Сэвиджа. По формуле (9)
не приводит к синтезированным решениям и каждая стратегия, оптимальная по критерию Вальда-Сэвиджа, оптимальна либо по критерию Вальда, либо по критерию Сэвиджа. По формуле (9) 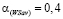 . Используя формулу (11), получим следующую структуру множества оптимальных не синтезированных стратегий по критерию Вальда-Сэвиджа
. Используя формулу (11), получим следующую структуру множества оптимальных не синтезированных стратегий по критерию Вальда-Сэвиджа
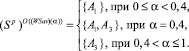
Условно-геометрическая интерпретация данной задачи представлена на рис. 5.
Найденное решение экономически можно проинтерпретировать следующим образом.
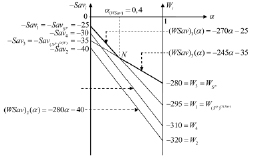
Рис. 5. Геометрическое представление задачи
Если значение выигрыш-показателя α находится в пределах 0 ≤ α < 0,4, то критерий Вальда-Сэвиджа рекомендует для изготовления продукции в качестве оптимального выбрать 1-й технологический способ (стратегия A1 в матрице R, оптимальная по критерию Сэвиджа), при котором предприятие гарантирует себе наибольший риск недостижения наименьших затрат при каждой потребности производимой продукции, равный 25 у.д.е (первая строка матрицы R). То есть, при выборе 1-го технологического способа производства риск недостижения наименьших затрат не может быть больше 25 у.д.е. При выборе другого способа производства этот риск может оказаться больше 25 у.д.е. Действительно, например, при выборе 2-го, 3-го или 4-го способа производства и при потребности соответственно в 50, 25 и 50 единиц продукции риск будет равен соответственно 40, 35 и 30 у.д.е (см. игровые ситуации (A2, П4), (A3, П1), (A4, П4) в матрице рисков R). Принятое решение является крайне пессимистическим относительно рисков, поскольку выбору 1-го технологического способа производства сопутствует наибольший при этом способе риск в 25 у.д.е.
Если значение выигрыш-показателя α находится в пределах 0,4 < α ≤ 1, то оптимальным по критерию Вальда-Сэвиджа является решение изготавливать продукцию по 3-му технологическому способу (стратегия A3 в матрице А оптимальна по критерию Вальда). При этом затраты предприятия при любой потребности в продукции составят не более 280 у.д.е. Если предприятие отклонится от оптимального решения и выберет 1-й, 2-й или 4-й способ производства, то при потребности в продукции в 50 единиц затраты составят соответственно 295, 320 или 310 у.д.е (см. игровые ситуации (A1, П4), (A2, П4), (A4, П4) в платежной матрице А). Принятое решение крайне пессимистично относительно издержек, так как при 3-м способе производства издержки в 280 у.д.е являются максимальными при этом способе производства.
Если α = 0,4 то с точки зрения критерия Вальда-Сэвиджа равноценными являются 1-й или 3-й способы производства.
Заключение
В статье рассмотрена проблематика корректности использования в процедурах выбора управленческих решений в условиях неопределенности, моделируемых в терминах «игры с природой», синтетического критерия, обобщающего свойства критериев, характеризующих принимаемое решение и с позиции возможного выигрыша, и с позиции возможного риска. Актуальность использования синтетического критерия связывается с необходимостью оценок качества принимаемого решения в условиях высокой неопределенности как в отношении выигрышей, так и сопровождающих их рисков. Предложенная интерпретация свойства синтезирования обобщенного критерия Вальда-Сэвиджа и доказанные условия наличия качества синтезирования этих критериев позволяют лицу, принимающему решения, обоснованно применять или не применять его в оценках игровой ситуации и при выборе окончательного решения.