Многопрофильное предприятие занимает видное место среди важных, но забытых тем в экономической теории. За исключением программных подходов поиск литературы не показывает всеобъемлющей теоретической трактовки предмета. Действительно, краткие выводы Хикса в математическом приложении к «Стоимости и капиталу» [11], вероятно, являются наиболее тщательной трактовкой в смысле рассмотрения как производственной, так и торговой деятельности предприятия. Поскольку Хикс выделяет всего четыре страницы на эту тему, это примечательное положение дел.
Хотя литература на всех этапах многопрофильного предприятия скудна, несколько авторов рассматривали торговую сторону такого предприятия; в этой связи можно привести работы Бейли [6], Клеменса [8] и Уэлдона [15]. На стороне «выпуск-затраты» литературы мало [1,4,5]. Даже работа Карлсона [7], стандартная ссылка на двадцать лет, касается только частного случая совместной стоимости, но не с каким-либо другим аспектом многопрофильного предприятия.
Цель исследования – представить теорию стоимости и производства для многопрофильного предприятия. При разработке этой теории сохранится традиционная концепция предприятия как социального механизма, связывающего рынки факторов производства с рынками готовой продукции. Это контрастирует с обычным «внутренним взглядом» предприятия, который появляется в литературе по экономико-математическому моделированию. Но как только проблема четко сформулирована в традиционных терминах, становится очевидным, что теорема Куна-Таккера, которую можно рассматривать как логическую основу методов оптимизации анализа деятельности, может быть однозначно использована для решения задач стоимости и производства на многопрофильном предприятии.
Материалы и методы исследования
Теперь мы обратимся к прямому рассмотрению «выпуск-затраты» на многопрофильном предприятии. Тип предприятия, которое мы рассматриваем, продает n разных продуктов, обозначенных xl, x2, ..., xn. При проведении этого производства используются переменные факторы производства, которые обозначены yij; Этот символ относится к количеству j-го переменного фактора, используемого при производстве i-го продукта. Термин «переменные факторы производства» относится к факторам, которые постоянно меняются с выходом и чьи общие объемы могут быть изменены предприятием в краткосрочной перспективе. Будем считать, что переменные факторы могут быть приобретены при постоянной цене единицы, хотя это предположение может быть изменено довольно легко. Мы обозначаем цену j-го переменного фактора wj.
Фиксированные факторы производства занимают важное место в теории многопрофильного предприятия. Термин «фиксированные факторы» относится, конечно, к факторам производства, которые не могут быть изменены в общей сумме в краткосрочной перспективе [5].
Важность фиксированных факторов в теории многопрофильного предприятия возникает частично из-за возможности переноса единиц фиксированного фактора из использования при производстве одного продукта к использованию при производстве другого продукта. Это служит для связывания продукции разных продуктов вместе. Таким образом, на предприятии каждый продукт конкурирует со всеми другими продуктами предприятия за использование доступных фиксированных факторов. Поэтому многопрофильное предприятие не может быть законно расценена как совокупность однопрофильных предприятий [2, 3].
Вторым источником особого значения фиксированных факторов в многопрофильном предприятии является тот факт, что доступное количество фиксированного фактора не может быть полностью использовано в течение любого периода эксплуатации. Такое условие не может существовать с переменными факторами, поскольку общее количество, используемое предприятием, может быть скорректировано в краткосрочной перспективе. По определению это не может быть сделано для фиксированных факторов. В краткосрочной перспективе может оказаться экономичным использование избыточной производительности в некоторых или во всех фиксированных факторах. Такая возможность обычно не рассматривается на предприятии с одним продуктом, но ее необходимо учитывать на многопрофильном предприятии.
В традиционных теоретических подходах к предприятию фиксированным факторам уделялось мало внимания. Вероятно, это связано с концентрацией на предприятии с одним продуктом, в которой нет никаких сомнений в распределении фиксированных факторов среди различных продуктов предприятия. Программный подход к предприятию выявил важность фиксированных факторов. Вероятно, Дорфман был первым, кто придал этому значение. В 1951 году он писал:
«Рассматриваемая в целом стоимость основных фондов фирмы заключается в том, что они предоставляют набор производственных возможностей, и мы уже видели, как можно (посредством программирования) выбрать оптимальный набор из этих возможностей» [9].
Аналогично, Дорфман, Самуэльсон и Солоу наблюдают:
«... в формулировке программирования, наиболее явно, когда ограничения являются линейными, величины фиксированных производственных факторов являются центральными для проблемы, поскольку они являются важными данными при определении того, что предприятие может делать и чего не может, в то время как в обычной формулировке эти же фиксированные факторы рассматриваются как несколько в стороне от проблемы только потому, что их величины фиксированы и предопределены» [10].
Чтобы ввести фиксированные факторы в нашу формулировку, напишем zit, чтобы представить количество t-го фиксированного фактора, используемого при производстве i-го продукта. Затем, используя Ft для обозначения общего количества фактора t, мы получаем ограничение деятельность предприятия в виде:
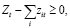(1)
где Zt – константа, и мы допускаем избыточную мощность в факторе t.
Также вводим понятие производственной функции в виде:
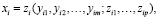
(i = 1,…,n). (2)
Уравнения (2) показывают величины n продуктов как функций от m переменных факторов производства и p фиксированных факторов производства. Предположим, что уравнения (2) неубывающие в диапазонах значений переменных, которые рассматриваем.
Перенос единиц фиксированных факторов из производства одного продукта в производство другого продукт обычно влечет за собой стоимость. Машины должны быть адаптированы для обработки другого продукта, должны быть изменены складские помещения и бункеры, здания должны быть отремонтированы и т.д. Здесь у нас есть тип затрат, который не существует на монопродовольственном предприятии и который не относится ни к категории переменных затрат, ни постоянных. Эти затраты не меняются непрерывно с выпуском конкретного продукта, но они меняются по мере изменения ассортимента продукта. Например, скорость выпуска продукта может быть увеличена до определенной точки за счет увеличения скорости работы машин. Такое увеличение изменяет переменные затраты и постоянные затраты на единицу, но это не вызывает никаких затрат на переключение фиксированных факторов из одного продукта в другой. С другой стороны, если количество машин, используемых при производстве продукта, увеличивается, и, если они должны быть адаптированы или откалиброваны, затраты на переключение фиксированного фактора на производство указанного продукта будут понесены. Таким образом, у нас есть тип стоимости, который ранее не рассматривался в теории фирмы.
Чтобы представить этот тип стоимости, пишем
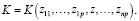(3)
Тогда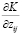 
которое считается положительным, представляет собой стоимость передачи небольшого количества фиксированного фактора j в производство продукта i. Чтобы проиллюстрировать тип стоимости, представленный (3), предполагаем, что такие затраты являются линейными. Пусть 
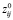представляет собой количество фиксированного фактора j, используемого при производстве продукта i в начале операционного периода, и 
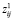– количество, используемое в течение операционного периода. Тогда, если aij – (постоянная)(constant) стоимость на единицу продукции по переводу фиксированного фактора j в обработку товара i, мы имеем
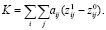(4)
Применительно к операционному периоду,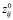 
постоянна; таким образом, мы имеем
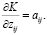(5)
Конечно, предположение о линейности используется только в целях иллюстрации.
Рассмотрим теперь центральную задачу, которая заключается в нахождении таких условий, при которых затраты сводятся к минимуму для любого фиксированного уровня выпуска каждого продукта, подверженного ограничениям, налагаемым общим количеством фиксированных факторов. Другими словами, мы хотим свести к минимуму сумму затрат на переменные факторы производства, затраты на передачу фиксированных факторов и постоянные затраты, представленные
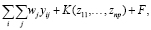(6)
с учётом
,
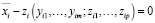(i = 1,…,n). (7)
и
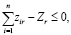(r = 1,…,p). (8)
Задача, сформулированная в уравнениях (6), (7) и (8), состоит в том, чтобы найти минимум функции, когда переменные функции ограничены неравенствами. Это тот тип проблемы, для обработки которого предназначена теорема Куна-Таккера, и, следовательно, представляется целесообразным использовать эту теорему. Хотя теорема является одним из общих математических интересов, она, как принято считать, обладает особой важностью для анализа активности (деятельности). Поскольку наш подход был сформулирован в традиционных терминах, возможно, следует кратко остановиться на различиях между этими двумя подходами.
Как отмечалось ранее, предприятие традиционно рассматривается как фактор покупки продукции на различных рынках факторов, сочетая их в продукте и продавая продукт на товарном рынке. Короче говоря, предприятие рассматривается в ее отношениях с остальной экономикой.
В программном подходе точка зрения совершенно иная. В этом контексте мы говорим о «действиях» или «процессах», а не о «факторах продукции». Затраты (inputs) в деятельность обычно не определяются непосредственно с точки зрения факторов производства, но могут быть указаны в любых удобных для проблемы условиях. Таким образом, внимание не сосредоточено на существующих рынках, а на доступных ресурсах (available inputs), возможно, после того как уже произошло несколько комбинаций факторов. Затраты (inputs) в деятельность могут быть указаны, например, с точки зрения возможностей линейных отделов предприятия. Разумеется, возможности отделов представляют собой комбинации различных факторов производства, но, возможно, нелегко думать о департаментах напрямую с точки зрения количества факторов производства. Программный подход ориентирован на управление, или, как выразился Дорфман, Самуэльсон и Солоу [10], он смотрит внутрь. Разумеется, нет никакого конфликта между этими двумя подходами.
В данной статье мы сохраняем традиционную концепцию предприятия, используя математическую логику, используемую в теории программирования.
Результаты исследования и их обсуждение
В теоретическом смысле методы программирования основаны на теореме Куна-Таккера, в которой рассматриваются экстремальные значения функций, ограниченных неравенствами [12]. Все программирование можно рассматривать как полагающееся на эту теорему, будь то линейное программирование или программирование с экстремальными значениями некоторой более сложной функции.
Теорема Куна-Таккера рассматривает задачу нахождения экстремальных значений функции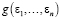 
, где переменные ограничены неравенствами, такими как
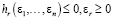, (r = 1,…,q). (9)
Поскольку мы обсудим применение теоремы к задаче минимизации, опишем теорему в терминах минимума, а не максимума.
Воздействие теоремы состоит в том, что задача локального минимума (constrained minimum problem) может при нестрогих ограничениях (under non-restrictive qualification) трансформироваться в задачу о седловой точке или максимине. Тогда условия, которые гарантируют нам седловую точку, также гарантируют нам локальный/ограниченный минимум (constrained minimum). Для того чтобы теорема была действительной, необходимо предположить, что g-функция и ограничения (9) являются выпуклыми и дифференцируемыми (существует еще одно незначительное ограничение на ограничения для исключения возможности особой точки (singular point) на границе ограничений [12]). Выпуклость означает, что линейная интерполяция между любыми двумя точками функции дает значение не меньше, чем значение функции в точке интерполяции. Теперь мы формируем лагранжево выражение,
+ 
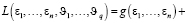
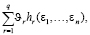(10)
εi ≥ 0, ϑr ≥ 0, (i = 1,…,n; r = 1,…,q).
Чтобы обеспечить существование ограниченного минимума в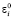 
и 
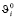необходимо и достаточно, чтобы седловая точка существовала при предельном значении. Чтобы обеспечить существование седловой точки, необходимо и достаточно, чтобы выполнялись следующие условия:
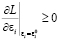, (i = 1,…,n), (11)
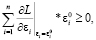(12)
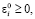(i = 1,…,n), (13)
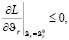(r = 1,…,q), (14)
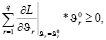(15)
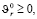(r = 1,…,q). (16)
Строгое неравенство будет выполнено в (11) только при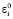 
= 0. Точно так же строгое неравенство будет выполняться в (14) только в том случае, если 
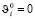, т.е. только, если r-е ограничение неэффективно.
Условия (11)–(16) обеспечивают ограниченный минимум в обозначенной точке. Теперь мы перефразируем эти условия в терминах отношений, связанных с многопрофильным предприятием. Таким образом, общие (валовые, total costs) затраты, которые мы хотим минимизировать и которые соответствуют g-функции выше, показаны в (6), а ограничения, которые соответствуют (9), показаны в (7) и (8).
Для того, чтобы применить теорему Куна-Таккера, необходимо, чтобы функции из (6), (7) и (8) были выпуклыми и дифференцируемыми. Последняя квалификация явно не вызывает проблем, если производственная функция и K-функция дифференцируемы, и такие предположения обычно считаются обоснованными в экономической теории. Общая стоимость (total cost) (6) может считаться выпуклой в пределах соответствующего диапазона выпуска, а также в соответствии с обычными эмпирическими предвзятостями экономической теории. Точно так же в экономической теории мы обычно соглашаемся, ссылаясь на закон убывающих возвращений, что производственные функции вогнуты и с учетом префиксов знаков минус производственные функции в (7) преобразуются из вогнутых в выпуклые функции. Ограничения в (8), являющиеся линейными, являются вогнутыми и выпуклыми. Таким образом, требования к выпуклости выполняются.
Теперь мы формируем соответствующее уравнение Лагранжа,
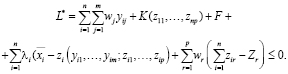(17)
Теперь в соответствии с (11) мы имеем
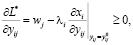
(i = 1,…,n; j = 1,…,m) (18)
и
,
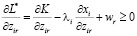при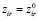 
(i = 1,…,n; r = 1,…,p). (19)
В (18) и (19)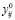 
и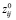 
означают минимальные значения этих переменных.
Из (18) мы наблюдаем, что если какой-либо из всех переменных факторов используется для производства каждого продукта, то равенства справедливы для всех факторов, и мы получаем знакомое условие, что предельная доходность последнего доллара должна быть одинаковой во всех областях применения. Если переменный фактор не используется при производстве конкретного продукта, выполняется неравенство, и обычное правило изменяется соответствующим образом, т.е. стоимость добавления фактора больше, чем продукт, полученный из фактора.
Отношения в (19) также представляют экономический интерес. Для упрощения обсуждения мы предполагаем, что для получения каждого продукта используется некоторый из каждого переменного фактора, и, следовательно, равенства выполняются в (18). Тогда в равновесии можно заменить λi из (18) на (19), получив
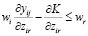
(i = 1,…,n; j = 1,…,m; r = 1,…,p). (20)
Таким образом, если j-й переменный фактор и r-й фиксированный фактор используются при производстве продукта i, то ωr – это разница между стоимостью корректировки переменного фактора из-за увеличения фиксированного фактора и стоимости увеличения использования фиксированного фактора в продукте i. Если в (20) выполняется строгое неравенство, то r-й фиксированный фактор не используется, поскольку стоимость корректировки некоторого переменного фактора больше стоимости переноса фиксированного фактора.
Если два переменных фактора и фиксированный фактор действительно используются при производстве двух продуктов предприятия, то из (19) мы, очевидно, имеем
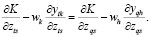(21)
Это уравнение выполняется независимо от наличия избыточной производительности в фиксированном факторе. Уравнения, подобные (21), требующие равенства предельных значений (marginal values) в равновесии, встречаются во многих контекстах экономической теории.
Отметим также, что если избыточная производительность существует в фиксированном факторе, соответствующее ограничение не является обязательным и (19) становится
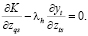(22)
И (18), и (22) могут быть решены для λ и полученное уравнение расширяет привычное предельное правило (marginal rule) в форме
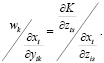(23)
Только в том случае, когда существует избыточная производительность во всех фиксированных факторах, которые обычно выполняются (23), и это единственный случай, когда в любом значимом смысле можно утверждать, что многопрофильное предприятие представляет собой просто набор монопродуктовых предприятий.
Из предыдущего обсуждения видно, что условия, соответствующие (12),
+ 
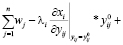
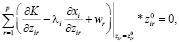
(i = 1,…,n) (24)
выполняются.
Мы должны также изучить условия в теории многопродукционного предприятия, соответствующие уравнениям (14). Из уравнения Лагранжа получаем
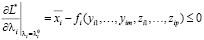
(i = 1,…,n). (25)
и
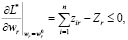
(i = 1,…,n). (26)
Из характера ограничения (7) ясно, что (25) всегда будет равным нулю. Для любого уравнения из (26), в котором нет избыточной производительности, знак равенства будет сохранён. Если в фиксированном факторе имеется избыточная производительность, то очевидно, что знак неравенства будет иметь место, а соответствующее ω будет равно нулю.
Нам также необходимо найти условия, соответствующие уравнениям (15) теоремы Куна-Таккера. Для многопрофильного предприятия имеем
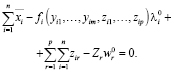(27)
Оценивается в λi = λ0i и ωr = ω0r. Из замечаний в предыдущем параграфе ясно, что (27) будет выполнено.
Наконец, заметим требование, соответствующее (13) и (16), что
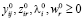
(i = 1,…,n; j = 1,…,m; r = 1,…,p). (28)
Ясно, что (28) справедливо для y-ов и z-ов, так как отрицательные количества факторов производства не определены в обсуждении. Ясно также, что λ-ы, выражая отношение цены фактора к предельному продукту (factor price to marginal product), будут определяться только как неотрицательная величина. Наконец, наблюдаем, что обсуждение, сосредоточенное на (20), демонстрирует экономический смысл того, что ω-и являются неотрицательными.
Заключение
Большая часть обсуждений в предыдущем разделе основана на отношениях, совершенно чуждых теорий предприятия с одним продуктом. Из условий равновесия только (18) и (25) аналогичны условиям, которые находятся в этой теории.
Аналогичным образом можно показать, что условия, которые находятся в равновесии монопродукционного предприятия, не сохраняются для многопрофильного предприятия. Например, Самуэльсон [14] выводит четыре условия для монопродуктового предприятия. Эти условия включают условие, аналогичное нашему уравнению (18), условие, требующее равенства перекрестных производных факторов затрат (inputs) в отношении ставок факторных платежей, условие о том, что при повышении цены фактора использование фактора будет сокращен (Макевер и Баумол показали, что если предприятие имеет ограниченные средства и должна со временем дозировать капитал, то условие снижения использования фактора с ростом цены не будет выполнено [8]), и, наконец, условие равенства между предельными издержками (marginal cost) и множителем Лагранжа. Из этих условий только первое имеет место в теории многопрофильного предприятия.
Конечно, есть некоторые сомнения в том, что эмпирически многопрофильное предприятие является более важной. И, конечно же, сейчас остаётся небольшое сомнение, что теория «выпуск-затраты» в обоих случаях сильно различается.