Введение
Построение экономико-математических моделей динамического развития производственных предприятий представляет собой одну из актуальных проблем современной экономической теории, успешное решение которой позволяет эффективно и адекватно анализировать деятельность предприятий, вычислять предельные показатели для производственных ресурсов, прогнозировать выпуск продукции, прибыль и затраты, оценивать эффекты замещения производственных факторов и т.д. [1–5].
Целью публикуемой работы является разработка новой трехфакторной экономико-математической модели развития предприятия, находящегося в условиях переоснащения производства. Эта модель представляет собой систему связанных нелинейных дифференциальных уравнений.
Особенность предлагаемой модели и ее научная новизна заключается в том, что она учитывает нелинейный характер амортизации производственных факторов. Кроме того, модель способна описывать различные варианты модернизации собственных производств. К таким вариантам относятся монотонный процесс развития предприятия, процесс временной стагнации работы предприятия или его временного сворачивания.
Математическая модель развития предприятия за счет внутренних инвестиций
Пусть некоторое производственное предприятие, выпуск готовой продукции которого обеспечивается тремя ресурсами в виде объемов факторов производства K, L, M.
Здесь объем K – образован основным капиталом и производственными фондами, объем L – представляет собой привлекаемые в производство трудовые ресурсы, объем M – состоит из используемых в производстве материалов, применяемых технологий, инноваций и т.д.
Выпуск продукции предприятия V обеспечивается трехфакторной производственной функцией Кобба–Дугласа
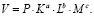(1)
Степенные показатели степени a, b, c – представляют собой эластичности выпуска продукции по каждому фактору производства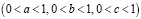 
, P – стоимость продукции произведенной на единичные объемы ресурсов.
Величины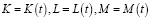 
считаются непрерывными, непрерывно дифференцируемыми и ограниченными на числовой полуоси 
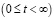функциями времени непрерывного аргумента t. Единицей измерения времени t служит соответствующий обстоятельствам рыночный период (месяц, квартал, год).
Функции объемов факторов производства удовлетворяют неравенствам
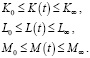
Здесь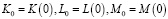 
– начальные значения факторов производства, 
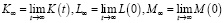– их предельные значения, которые подлежат вычислению.
Рассмотрим сначала процесс развития предприятия только за счет внутренних инвестиций. Составим уравнения баланса динамики развития рассматриваемого предприятия для объемов факторов производства K, L, M. Приращения объемов факторов производства ΔK, ΔL, ΔM за некоторый малый промежуток времени Δt образуются из двух компонентов
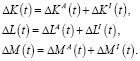(2)
Здесь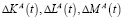 
– приращения амортизаций факторов производства, 
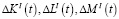– приращения частичных восстановлений факторов производства за счет внутренних инвестиций.
Приращения частичных амортизаций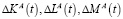 
за промежуток времени Δt можно представить в виде [6]
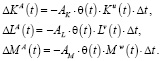(3)
Здесь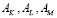 
– коэффициенты амортизации, доли выбывших за единицу времени объемов факторов производства, u, v, w – показатели интенсивности амортизации. Если эти показатели равны единице, то имеет место обычная пропорциональная амортизация. Если показатели больше единицы, то амортизационные отчисления увеличиваются и становятся прогрессивными. Если же эти показатели меньше единицы, то амортизационные отчисления снижаются и становятся регрессивными.
Приращения внутренних инвестиций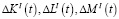 
за промежуток времени Δt определяются соотношениями
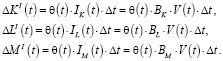(4)
Здесь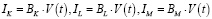 
– инвестиции, вложенные в факторы производства K, L, M в момент времени t, 
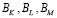– нормы накопления внутренних инвестиций.
Функция θ(t) в формулах (3) и (4) определяет уровень приращений факторов производства и описывает в конечном счете удельную скорость развития рассматриваемого предприятия. Если функция θ(t) постоянна и равна единице 
, то уровень приращений факторов производства будет максимальным, а само развитие предприятия будет поступательным и монотонно возрастающим. Если функция θ(t) принимает значения меньше единицы, то развитие предприятия будет замедляться, вплоть то временной остановки или даже до некоторого сворачивания производства [7].
В пределах жизненного цикла предприятия как правило наступает период, в котором применяемые в производстве технологии морально устаревают и начинают тормозить процесс выпуска продукции. В этом временном интервале значения функции θ(t) становятся меньше единицы. Обновление имеющихся производственных технологий или внедрение новых, перевооружение и модернизация производства могут привести к обратному росту этой функции.
Подставляя формулы (3) и (4) в уравнения баланса (2), получаем
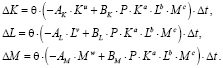
Переходя здесь к пределу при условии Δt → 0, находим систему нелинейных дифференциальных уравнений
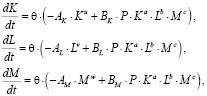(5)
c начальными условиями
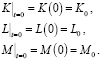(6)
Поскольку формирование штатного расписания не всегда является экономической задачей, то следует отметить, что выражение объема фактора трудовых ресурсов L в денежной форме напрямую не связано с численностью персонала рассматриваемой экономической системы. Здесь не исключены варианты, в которых увеличение фактора L может сопровождаться как уменьшением, так и увеличением числа работников и наоборот.
Структура уравнений (5) показывает, что развитие предприятия будет происходить до тех пор, пока объемы внутренних инвестиций –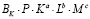 
, 
, 
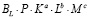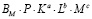будут превосходить соответсвующие амортизационные отчисления – 
, 
, 
.
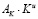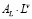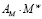Предельные значения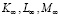 
объемов производственных факторов 
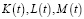находятся из системы уравнений
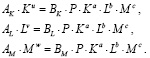(7)
Решение системы (7) имеет вид
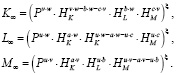(8)
Здесь
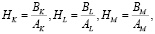
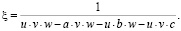
Таким образом, предельное значение выпуска продукции предприятием выражается формулой
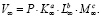(9)
Динамика выпуска продукции предприятием V(t) рассчитывается по формуле (1) после решения задачи Коши (5), (6)
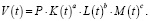(10)
Форма кривой (10) существенно зависит от вида функции θ(t), которая определяют центр временного интервала, его протяженность и размер отклонения от единичного значения, при котором предприятие работает стабильно.
Если в некотором симметричном временном интервале с центром в точке времени t = t* на предприятии производится некоторая замена технологического оборудования или происходит временное сворачивание производства, то функцию θ(t) можно принять в виде 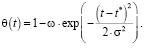[1]
(11)
Здесь ω – максимальный размер отклонения функции θ(t) от единицы, σ – радиус временного интервала смены технологического уклада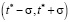 
.
Если параметр ω = 0, то предприятие будет работать стабильно и выпуск его продукции будет монотонно возрастать, если параметр ω = 1, то в момент времени t = t* рост функции выпуска V(t) прекращается, и на интервале времени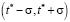 
происходит переоснащение производства, если параметр ω > 1, то на интервале времени 
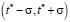происходит переоснащение производства, сопровождаемое его некоторым сворачиванием.
Если эффекты стагнации и падения выпуска продукции на предприятии происходят неоднократно, то в качестве функции относительной удельной скорости развития рассматриваемого предприятия целесообразно выбрать произведение функций вида (11)
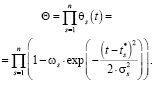(12)
На рис. 1 приведены графики функций выпуска продукции предприятия V(t), построенные по результатам численного решения задачи Коши (5), (6), для случая стабильной работы предприятия, при котором параметр ω = 0, для случая переоснащения производства предприятия, при котором параметр ω = 1, и для случая определенного временного сворачивания производства предприятия, при котором параметр ω > 0.
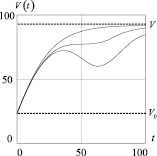
Рис. 1. Графики функций выпуска продукции предприятия V(t), построенные по результатам численного решения задачи Коши (5), (6), для различных режимов работы предприятия
Расчетные значения величин: P = 3; a = 0,34; b = 0,25; c = 0,2; u = 1,12; v = 1,14; w = 1,16; K0 = 20; L0 = 10; M0 = 10; AK = 0,1; BK = 0,15; AL = 0,1; BL = 0,15; AM = 0,1; BM = 0,15; K∞ = 82,034; L∞ = 75,930; M∞ = 70,468; V0 = 23,414; V∞ = 92,807; t* = 50; σ = 15.
Математическая модель развития предприятия за счет внутренних и внешних инвестиций
Обобщим теперь рассмотренные выше уравнения развития предприятий на случай, когда помимо внутренних инвестиций в производство вкладываются и внешние инвестиции. Составим уравнения баланса динамики развития рассматриваемого предприятия для объемов факторов производства K, L, M. Приращения объемов факторов производства ΔK, ΔL, ΔM за некоторый малый промежуток времени Δt образуются из трех компонентов
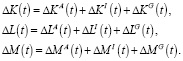(13)
Здесь приращения амортизаций факторов производства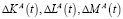 
, приращения частичных восстановлений факторов производства за счет внутренних инвестиций 
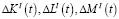по-прежнему задаются формулами (3) и (4).
Приращения внешних инвестиций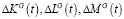 
за промежуток времени Δt могут быть представлены формулами
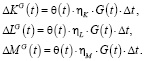(14)
Здесь G(t) – объем внешних инвестиций, приходящихся на объемы факторов производства K, L, M,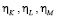 
– коэффициенты распределения объема внешних инвестиций G(t) между объемами факторов производства K, L, M. Очевидно, что коэффициенты 
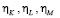не являются независимыми, а удовлетворяют соотношению
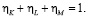
Подставляя формулы (3), (4) и (14) в уравнения баланса (13), получаем
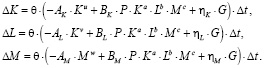
Переходя здесь к пределу при условии Δt → 0, находим систему нелинейных дифференциальных уравнений
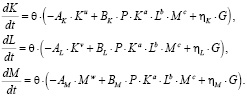(15)
Начальными условиями для системы (15) по-прежнему являются условия (6).
Вид функции объема внешних инвестиций G(t) существенно зависит от условий инвестирования. Если, например, предприятие находится в условиях со финансирования с внешним инвестором, то уровень объема внешних инвестиций будет соответствовать уровням объемов производственных факторов. В таком случае функция G(t) будет представлять собой дополнительную производственную функцию от факторов производства K(t), L(t), M(t)
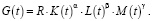(16)
Степенные показатели степени α, β, γ – представляют собой эластичности внешних инвестиций по каждому фактору производства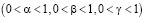 
, R – стоимость привлеченных внешних инвестиций на единичные объемы ресурсов.
Таким образом, система уравнений (15) принимает вид
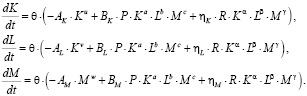(17)
Структура уравнений (17) показывает, что развитие предприятия будет происходить до тех пор, пока объемы внутренних и внешних инвестиций будут превосходить соответсвующие амортизационные отчисления. Предельные значения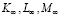 
объемов производственных факторов K(t), L(t), M(t) находятся из системы уравнений
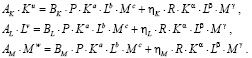(18)
В общем случае систему уравнений (18) можно решить только численно в отличие от системы (7), которая имеет аналитическое решение (8).
Если уровни объемов внешних инвестиций не зависят от уровней объемов производственных факторов, то функция G(t) задается непосредственно, исходя из наблюдаемых статистических данных.
Рассмотрим вариант развития предприятия, при котором максимальный объем внешних инвестиций Gmax вкладывается в производство в начальный момент времени, а затем их уровень постепенно снижается до определенного предела Gmin. Уменьшение объема внешних инвестиций G(t) за время Δt будем предполагать пропорциональным отклонению функции G(t) от минимального значение этих инвестиций Gmin
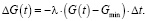
Переход к пределу при условии Δt → 0 дает дифференциальное уравнение для функции G(t)
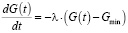, (19)
решение которого с начальным условием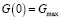 
дает объем внешних вложений в предприятие в виде
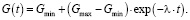(20)
Здесь константа Gmax представляет собой максимальную стоимость привлеченных внешних инвестиций, λ – параметр, характеризующий скорость снижения объемов внешних инвестиций.
На рис. 2 приведен график функции (20) c расчетными значениями: Gmax = 15; Gmin = 3; λ = 0,05.
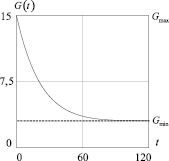
Рис. 2. График функции объемов внешних инвестиций, построенный по формуле (19)
Структура уравнений (15) с функцией (20) показывает, что развитие предприятия будет происходить до тех пор, пока объемы внутренних и внешних инвестиций будут превосходить соответсвующие амортизационные отчисления. Предельные значения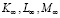 
объемов производственных факторов K(t), L(t), M(t) находятся из системы уравнений
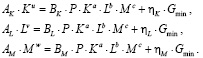(21)
В общем случае систему уравнений (21) можно решить только численно в отличие от системы (7), которая имеет аналитическое решение (8).
На рис. 3 приведены графики функций выпуска продукции предприятия V(t), построенные по результатам численного решения задачи Коши (15), (6), для случая стабильной работы предприятия.
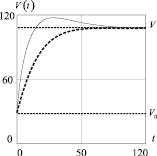
Рис. 3. Графики функций выпуска продукции предприятия V(t), построенные по результатам численного решения задачи Коши (15), (6), для случая стабильной работы предприятия. Верхняя сплошная линия соответствует решению задачи Коши (15), (6), с функцией объема внешних вложений (20). Нижняя штриховая линия соответствует решению задачи Коши (15), (6), с постоянным минимальным объемом внешних вложений (20) G(t) = Gmin
Расчетные значения величин: P = 3; a = 0,34; b = 0,25; c = 0,2; u = 1,12; v = 1,14; w = 1,16; K0 = 20; L0 = 10; M0 = 10; AK = 0,1; BK = 0,15; AL = 0,1; BL = 0,15; AM = 0,1; BM = 0,15; Gmax = 15; Gmin = 3; λ = 0,05; ηK = 0,5; ηL = 0,3; ηM = 0,2; K∞ = 101,370; L∞ = 90,685; M∞ = 82,630; V0 = 23,414; V∞ = 107,632; ω = 0.
Рассмотрим еще один вариант развития предприятия, при котором внешние инвестиции вкладываются в производство на небольшом временном интервале. При этом эти инвестиции сначала увеличиваются до своего максимального значения, а затем прекращаются совсем.
Такие объемы внешних вложений в предприятие можно описать формулой
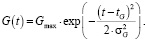(22)
Здесь константа Gmax представляет собой максимальную стоимость привлеченных внешних инвестиций, tG – момент времени, отвечающий максимальному значению внешних инвестиций, σG – радиус временного интервала вложения внешних инвестиций.
На рис. 4 приведен график кривой функции (22) с расчетными значениями: Gmax = 15; tG = 50; σG = 10.
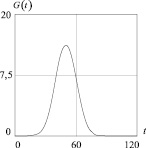
Рис. 4. График функции объемов внешних инвестиций, построенный по формуле (22)
На рис. 5 приведены графики функций выпуска продукции предприятия V(t), построенные по результатам численного решения задачи Коши (15), (6), для случая стабильной работы предприятия.
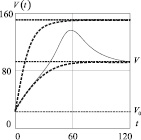
Рис. 5. Графики функций выпуска продукции предприятия V(t), построенные по результатам численного решения задачи Коши (15), (6), для различных режимов работы предприятия. Сплошная линия соответствует случаю, когда внешние инвестиции задаются формулой (22). Верхняя штриховая линия соответствует решению задачи Коши (15), (6), с постоянным максимальным объемом внешних вложений (20) G(t) = Gmax. Нижняя штриховая линия соответствует решению задачи Коши (15), (6), с нулевым объемом внешних вложений (20) G(t) ≡ 0
Расчетные значения величин: P = 3; a = 0,34; b = 0,25; c = 0,2; u = 1,12; v = 1,14; w = 1,16; K0 = 20; L0 = 10; M0 = 10; AK = 0,1; BK = 0,15; AL = 0,1; BL = 0,15; AM = 0,1; BM = 0,15; Gmax = 15; Gmin = 1; λ = 0,05; ηK = 0,5; ηL = 0,3; ηM = 0,2; K∞ = 88,808; L∞ = 81,139; M∞ = 74,784; V0 = 23,414; V∞ = 98,099; t* = 50; σ = 15.
Заключение
Разработаны новые модели динамики развития предприятий, восстановление производственных мощностей которых происходит за счет внутренних и внешних инвестиций.
Построенные математические модели представляют собой системы дифференциальных уравнений относительно трех производственных факторов, в качестве которых использовались объем основного капитала, объем привлекаемых в производство трудовых ресурсов и объем применяемых в производстве материалов.
Составленные из решений этих систем динамические производственные функции способны описывать различные варианты развития выпуска продукции предприятиями.
Рассмотрены случаи монотонного поступательного выпуска продукции предприятиями, временной приостановки работы предприятий при их техническом переоснащении, и временное сворачивание производства.
Исследовано взаимодействие пропорциональных, прогрессивных и дигрессивных амортизационных отчислений с внутренними и внешними инвестициями, и получены уравнения для вычисления предельных объемов производственных факторов предприятий.