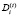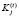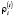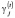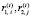Научный журнал

Вестник Алтайской академии экономики и права

Print ISSN 1818-4057

Online ISSN 2226-3977

Перечень ВАК

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Горский М.А. 1

---

1 Российский экономический университет им. Г.В. Плеханова

Рост доходности банковских операций и расширение объемов банковского кредитования розничных и корпоративных заемщиков предполагает совершенствование теории и практики оценки внешних и внутренних рисков банковской организации и выбора нормативов, регулирующих ее кредитно-депозитную деятельность. В качестве вполне оригинального инструментария решения этой задачи в работе представлена концепция параметрического моделирования оптимального банковского портфеля депозитов-ссуд. Предложено в качестве управляемых параметров банковского портфеля выбрать те, которые находятся в регулируемом менеджментом банка поле: величина резервов, уровни ликвидности, процентные ставки, кредитный риск портфеля и некоторые др. Учитывая влияние параметров на структуру и состав банковского портфеля, предложено на основе эмпирических расчетов выбрать такую их комбинацию, которая позволила бы повысить его доходность при соблюдении ограничений, определяемых с использованием этих параметров. В работе приводятся результаты выбора оптимального варианта кредитно-депозитной деятельности универсального коммерческого банка среднего по объему капитала (близкого по характеристикам к КБ Промсвязьбанк), полученные на основе расчетов по параметрической модели, которые продемонстрировали адекватность предложенного подхода и модели кредитно-инвестиционной практике современного российского банка.

Статья в формате PDF

0 KB

коммерческий банк

портфель депозитов-ссуд

кредитно-инвестиционная деятельность

математическое моделирование

параметрическая модель банка

кредитная стратегия банка

нормативы банковской деятельности

1. Бренд Р. Банковская система и контроль за банковской деятельностью в условиях рыночной экономики. Мюнхен. 1994. 426 с.

2. Егорова Н.Е., Смулов А.М. Предприятия и банки: Взаимодействие, экономический анализ: учебно-практическое пособие. М.: Дело, 2002. 454 с.

3. Киселева И.А. Система математического моделирования банковской деятельности в переходной экономике / Дис. на соис. уч. ст. д.э.н. М.: МЭСИ, 2000. 484 с.

4. Лаврушин О.И. Деньги, кредиты, банки. М.: Кнорус. 2014. 448 с.

5. Центральный банк Российской Федерации [Электронный ресурс]. URL: https://www.cbr.ru/today/cbrf_itm/cbrf_sub// (дата обращения: 10.12.2019).

6. Klin M. Theory of the banking firm. J.Money. Credit and banking. 1971, May. Р. 205-218.

7. Maximov D.A., Khalikov M.A. Prospects of institutional approach to production corporation assets assessment. Aktual Problems of Economics. 2016. vol. 183. № 9. P. 16-25.

8. Буруханова Т.Д. Оптимизация кредитного портфеля коммерческого банка. / Дис. на соис. уч. ст. к.э.н. М.: Фин. Акад. при Правительстве РФ. 2003 г. 140 с.

9. Рогачев А.Ю. Современная роль коммерческих и региональных банков // Экономический журнал ВШЭ. 2004. № 1. С. 92-96.

10. Халиков М.А., Максимов Д.А. О приоритетной модели российской экономики. // Международный журнал прикладных и фундаментальных исследований. 2015. № 4-2. С. 309-310.

11. Халиков М.А., Антиколь А.М. Методы учёта трансакционных издержек операций фондового рынка // Вестник Российского экономического университета. 2012. № 2. С. 53-59.

12. Роуз Питер С. Банковский менеджмент. М.: Дело, 1997. 768 с.

13. Синки Джозеф Ф., мл. Управление финансами в коммерческих банках. Пер. с англ.: под ред. Р.Я. Левиты, Б.С. Пинскера. М.: Catallaxary, 1994. 957 с.

14. Busch A. Banking regulation and globalization / A. Busch. Oxford: Oxford: University Press, 2009. 282 р.

15. Murphy N.D. Costs of banking activities: interactions between risk and operating costs: comment. J. Money // Credit and Banking. 1972. Aug. Р.205-218.

16. Sealey C.W. Valuation, capital structure, and shareholder unanimity for depository financial intermediates// J. Finance. 1983, June. Р. 1139-1154.

17. Гаджиагаев (Горский) М.А., Халиков М.А. Динамическая модель оптимального управления кредитным портфелем коммерческого банка с дополнительным критерием ликвидности временной структуры активов-пассивов// Путеводитель предпринимателя. 2016. № 29. С. 72-85.

18. Горский М.А., Алексеева А.А., Решульская Е.М. Устойчивость и надежность коммерческого банка в турбулентной рыночной среде // Фундаментальные исследования. 2019. № 2. С. 60-68.

19. Информация о банковской системе Российской Федерации, [Электронный ресурс]. URL: https://www.cbr.ru/finmarket/lic/ (дата обращения: 21.12.2019).

20. Информация о кредитно-инвестиционном банке «Промсвязьбанк» [Электронный банк]. URL: https://www.banki.ru/banks/bank/promsvyazbank/ (дата обращения: 20.12.2019).

21. Кредитный портфель банка | Банки.ру [Электронный ресурс]. URL: https://www.banki.ru/ (дата обращения: 20.12.2019).

23. Система анализа финансового состояния банков, [Электронный ресурс]. URL: https://analizbankov.ru/index.php (дата обращения: 20.12.2019).

24. Антиколь А.М., Халиков М.А. Нелинейные модели микроэкономики: уч. пос. М.: ФГБОУ ВПО «РЭУ им. Г.В. Плеханова», 2011. 156 с.

25. Халиков М.А., Хечумова Э.А., Щепилов М.В. Модели и методы выбора и оценки эффективности рыночной и внутрифирменной стратегий предприятия/ Под общ. ред. проф. Халикова М.А. М.: Коммерческие технологии. 2015. 595 с.

26. Мину М. Математическое программирование. Теория и алгоритмы. М.: Наука, 1990. 488 с.

27. Халиков М.А. Дискретная оптимизация планов повышения надежности функционирования экономических систем // «Финансовая математика» Сб. ст. М.: МГУ. 2001. С. 281-295.

Введение

Структурная перестройка экономики России с упором на опережающее развитие инновационных производств и создание высокопроизводительных рабочих мест предполагает значительные инвестиции в реальный сектор экономики и софинансирование инвестиционных проектов российских корпораций с привлечением банковских кредитов. В этих условиях значительно возрастает роль банковского сектора, в том числе и коммерческих банков.

На современном этапе развития экономики России основным препятствием расширенному кредитованию банками инвестиционных программ экономических агентов является неполнота и неточность информации о перспективах финансовых рынков, финансово-экономическом положении ссудополучателей, рисках кредитования и портфельного инвестирования. Банки вынуждены перестраховываться, увеличивать резервы, сокращать долю работающих активов, что негативно сказывается на их доходности и конкурентоспособности.

Вместе с тем, решение проблемы оптимизации деятельности кредитного учреждения, связанной с выбором наилучшего из имеющихся вариантов формирования банковского портфеля депозитов-ссуд, лежит в хорошо известной и в целом достаточно разработанной предметной области экономических и математических дисциплин, использующих методы исследования операций, оптимального управления и математического моделирования.

Указанное актуализирует проблематику совершенствования известных и разработки оригинальных экономико-математических моделей и численных методов оптимального управления банковским портфелем с учетом приоритетов кредитно-депозитной деятельности банка (в ряду которых отметим рост финансовой устойчивости кредитной деятельности, безусловное обеспечение надежности в соответствии с нормативами ЦБ и международными стандартами, сохранение и повышение конкурентоспособности банка в основных направлениях деятельности [1–7]), условий и ограничений этой деятельности, определяемых параметрами финансовых рынков, внешними и внутренними нормативами.

Научно-практический задел и методологические основы работы

Проблематика оценки эффективности коммерческого банка и оптимального управления кредитно-депозитным портфелем, в том числе, обоснования критериев оптимальности и экономико-математического моделирования банковского портфеля исследована в трудах российских: Бурухановой Т.Д. [8], Егоровой Н.Е. и Смулова А. [2], Киселевой И.А. [3], Лаврушина О.И. [4], Рогачева А.Ю. [9], Халикова М.А. и Максимова Д.А. [10], Халикова М.А. и Антиколь А.М. [11] и авторитетных западных: Бренда Р. [1], Роуза П. [12], Синки Дж. [13], Буша А. [14], Клини М. [6], Мэрфи Н. [15], Сили К. [16] и др. ученых и банковских аналитиков.

В этой, как и более ранних работах автора (например, [17,18]), будем использовать «производственную» интерпретацию «банковской фирмы», широко применяемую в цитируемых выше работах Клини М. и Мэрфи Н. Такой подход оказывается вполне оправданным в случае использования в процедурах формирования и управления банковским портфелем различных экономико-математических моделей: оптимизационных, стохастических, балансовых, теории безкоалиционных и коалиционных игр и т.п.

Как отмечено выше, в настоящее время особую важность приобретают исследования, связанные с совершенствованием теоретических моделей и практических приемов управления кредитно-депозитной деятельностью российских коммерческих банков в направлении уточнения критериев оптимальности, внешних (определяемых регулятором) и внутренних (вытекающих из приоритетов банковской стратегии и определяемых внутренними нормативами) ограничений на выбор процентных ставок и уровень кредитного риска.

Оптимальное сочетание внешних и внутренних нормативов в задачах управления банковским портфелем по мысли автора может быть определено на основе параметрического моделирования портфеля депозитов-ссуд, в котором планируемые банком внутренние нормативы выступают в роли параметров, оценка корректности выбора которых устанавливается в соответствии со значениями предварительно установленных критериев оптимальности кредитно-депозитной деятельности банка. Достаточно общее описание параметрической модели банка приведено в работе автора с соавторами [18].

Целью этой работы является более подробное описание параметрической модели банковского портфеля с обоснованием критерия оптимальности и выбираемых в качестве параметров эндогенных переменных.

Результаты работы и их обсуждение

Модельные расчеты по параметрической модели проводились на данных кредитно-инвестиционного портфеля банка XXX, характеристики которого близки к характеристикам коммерческого банка Промсвязьбанк, являющегося крупным универсальным банком с развитой сетью подразделений. Ключевыми направлениями его работы традиционно являются кредитование и обслуживание счетов корпоративных клиентов [5, 19, 20, 21]. С недавних пор банк развивает розничный бизнес, оказывая полный спектр услуг розничным и корпоративным клиентам, малому и среднему предпринимательству. Этот банк был выбран в качестве «опорного» для финансирования государственного оборонного заказа и сопровождения крупных государственных контрактов. Банк активно ведет политику на межбанковском и валютном рынках, на рынке ценных бумаг.

Учитывая необходимость оперирования официальной информацией, нами выбраны ставки кредитов и депозитов за период 2016–2018 гг.

Для оптимизации портфеля Банка ХХХ в условиях неполной и неточной информации о рынках депозитов и ссуд была использована параметрическая модель выбора оптимального варианта кредитно-депозитной деятельности в статичном варианте [18].

Основные параметры, используемые в формальном представлении параметрической модели оптимального банковского портфеля, приведены в таблице 1.

Таблица 1

Также в состав переменных модели оптимального банковского портфеля включены:

T – временной горизонт планирования кредитно-инвестиционной деятельности банка, t-плановый период (t = 1,…,T);

I(t) – число депозитов, открытых в банке к началу периода t;

J(t) – число кредитов и других инвестиций, включенных или рассматриваемых с позиции возможного включения банковский портфель к началу периода t;

Депозит и депозитная ставка связаны следующим соотношением:

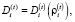(1)

где Di – функция (в общем случае нелинейная), задающая зависимость величины депозита от процентной ставки ;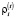

Кредиты и кредитная ставка, в свою очередь, связаны соотношением:

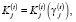(2)

где Kj – функция (в общем случае нелинейная), задающая зависимость величины кредита от кредитной ставки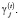

К элементам пассивов и активов банка, чувствительным к изменениям соответствующих процентных ставок для периода t, относятся соответственно Di(t) и Kj(t):

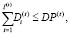(3)

где DP(t) – предельная для периода t величина сбережений, которая может быть размещена в депозиты;

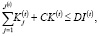(4)

где CK(t) – собственный капитал банка в ликвидной форме; DI(t) – потенциальная емкость инвестиционного рынка (для периода t).

Баланс банка для периода t задается неравенством:

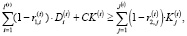(5)

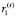где и 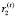– ставки обязательного резервирования, соответственно: 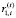– норматив по резервированию средств в ЦБ, зависящий от вида депозита; 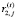– норматив отчисления по j-му кредиту (инвестиции) в резервы банка, зависящий от риска невозврата [5, 21, 22].

Следующее ограничение – на гэп-разницу величин активов и пассивов, чувствительных к изменению ставки процента и подлежащих переоценке или погашению к фиксированному сроку (стабилизатор кредитно-инвестиционной стратегии коммерческого банка [21]):

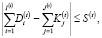(6)

где S(t) – предельная для временного периода t величина дисбаланса кредитно-депозитной структуры банка (проблематика моделирования кредитно-депозитной деятельности коммерческого банка с учетом риска ликвидности временной структуры активов-пассивов подробно рассматривалась в работах Бурухановой Т.Д. [8] и автора [17], а также в работах Егоровой Н.Е. [2] и Киселевой И.А. [3]).

В нашем случае возможный дисбаланс должен быть в пользу активной инвестиционной стратегии банка, а, следовательно, ограничение (6) принимает вид неравенства:

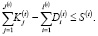(7)

Следующее ограничение – на текущую ликвидность баланса активно-пассивных операций:

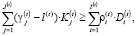(8)

где l(t) – норматив текущей ликвидности для периода t, определяемый регулирующим органом (ЦБ) [5, 21].

Отметим, что Центральный банк РФ ежегодно предоставляет данные о нормативах [5]. Один из них – норматив текущей ликвидности, который ограничивает риск потери банком платежеспособности в течение ближайших (к дате формирования портфеля) 30 дней (минимальное значение показателя – 50 %) [5]. В параметрической модели банка также предложено использовать значение норматива 50 %.

Расчеты были оптимального портфеля банка ХХХ проводились на информационной базе за период 2016-2018 гг. Были использованы данные о 10 кредитах и 10 депозитах, взятых и выданных под различные ставки и на суммы от 50 тыс. руб. до 700 тыс. руб. (таблица 2).

Отметим наиболее часто применяемые в банковской практике критерии, используемые в моделях оптимального банковского портфеля (тематика выбора и обоснования критериев кредитно-инвестиционной деятельности универсального коммерческого банка подробно рассматривалась в работах автора [17, 18]):

а) максимум процентной маржи (без учета риска невозврата кредита):

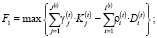(9)

или (с учетом):

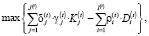(9')

где 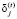– доля невозвращаемых кредитов (зависящая, в том числе, от ставки );

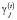б) максимум взвешенной суммы процентной маржи, и банковских резервов:

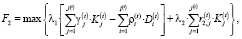(10)

где 0 ≤ λ1, λ2 ≤ 1; λ1 + λ2 = 1;

в) на максимум процентной маржи (с учетом или без учета риска невозврата кредита) на руб. доходных активов:

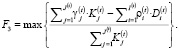(11)

В Таблице 3 представлены результаты расчетов показателей F1, F2, F3 на основе официальной информации о депозитах, кредитах и резервах банка ХХХ за период 2016 – 2018 гг.

Таблица 3

Значения критериев оптимальности кредитно-инвестиционной деятельности банка ХХХ

По данным таблицы 3 можно сделать предварительный вывод о одинаковой направленности исследуемых показателей качества банковского портфеля с позиции акционеров и других собственников. Однако в качестве критерия в параметрической модели оптимального банковского портфеля следует рассматривать один из абсолютных критериев (F1 или F2), так как критерий в форме F3 носит ярко выраженный «долевой» характер, что ограничивает возможности его использования в качестве критерия в экономико-математических моделях, в том числе и параметрических, ввиду возможности искажения решения по причине «эффекта структуры» (эта особенность задач математического программирования рассмотрена, например, в работе Антиколь А.М. и Халикова М.А. [23]).

Необходимо также отметить и следующее обстоятельство: вышеперечисленные критерии не применимы в задачах стратегического планирования кредитно-депозитной деятельности банка, так как они ориентированы на выбор портфеля на текущем временном отрезке.

В качестве целевого ориентира долгосрочный стратегии банка, ориентированной на стабильный рост доходности и инвестиционной привлекательности кредитно-депозитной деятельности, обеспечение финансовой устойчивости и снижение риска, должны выбираться стоимостные показатели, основанные на оценках денежных потоков банка.

Таким показателем может служить стоимость дисконтированного чистого денежного потока банка, принадлежащего акционерам, или производные от этого показателя (например, стоимость денежного потока, приходящаяся на ед. акционерного капитала. Актуальность использования указанного показателя в оценках качества предпринимательских решений и, в том числе, в банковской сфере, обоснована в работах проф. Халикова М.А. и его учеников [7, 10, 24]). Стоимость акционерного капитала, который отражает оценку основной деятельности коммерческого банка, является важным стоимостным показателем.

С учетом приведенных обоснований в качестве интегрального критерия оптимальности кредитно-депозитной деятельности коммерческого банка предложен показатель дисконтированной стоимости накопленной процентной маржи:

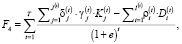(12)

где T – рассматриваемый стратегический горизонт; e – ставка дисконтирования (исходя из рекомендаций, представленных в цитируемых выше работах [7, 10, 24] – средневзвешенная стоимость капитала банка – постоянная (если структура капитала на горизонте планирования остается постоянной) или переменная (в противном случае).

Для выбранного банка ХХХ этот критерий на анализируемом временном интервале имел следующие значения (табл. 4).

Исходя из данных, представленных в таблице 4, можно сделать вывод, что динамика предложенного интегрального показателя оптимальности кредитно-инвестиционной деятельности коммерческого банка в полной мере согласуется с динамикой частных показателей F1, F2, F3, что является дополнительным аргументом в пользу его использования в качестве целевого критерия оптимальности в параметрической модели банка.

Таблица 4

Значения критерия F4 оптимальности кредитно-инвестиционной деятельности банка ХХХ

Рассматривая систему ограничений параметрической модели банка, сделаем следующее замечание. Если стратегический горизонт превышает некоторое (определенное экспертами-банковскими аналитиками и заранее известное) число плановых периодов (месяцев, лет), то необходимо дополнительно учитывать ограничение на минимальный уровень рентабельности доходных активов (для стимулирования активности кредитно-инвестиционной политики банка на каждом плановом интервале):

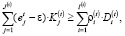(13)

где ε – пороговое значение рентабельности доходных активов.

Разобьем множество индексов I(t) депозитов и J(t) кредитов на множества 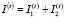и 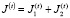, включив в 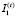действующие депозиты, а в 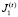– действующие кредиты и профинансированные инвестиции прошлых периодов. Будем считать такое разбиение корректным, а именно, включенные в эти множества пассивы и активы удовлетворяют ограничениям (1) – (8), (13).

Параметрическая модель банка в статичном для временного интервала t варианте включает критерий (9) (на максимум) и ограничения (1) – (8), (13). Эндогенными (управляемыми) переменными модели являются доступные банку депозиты с индексами из множества 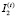и кредиты с индексами из множества .

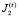Если рассматривать динамический вариант параметрической модели коммерческого банка, то необходимо дополнительно учесть балансовые соотношения, связывающие величины пассивов и активов.

Выделим в составе депозитов срочные обязательства до востребования DS, межбанковские кредиты и векселя DV, прочие депозиты DP.

Считая, что ΔCK(t) – изменение собственного капитала банка на временном интервале t, определим пошаговые ограничения на величины составляющих пассива:

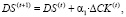
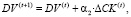(14)

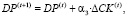
α1, α2, α3 ≥ 0, α1 + α2 + α3= 1,

где α1, α2, α3 – доли распределения прибыли по составляющим пассивов.

В составе активов, в свою очередь, выделим ликвидные AL (ставка rAL процента), средне- и низколиквидные AS (ставка rAS процента).

Пошаговые ограничения по составляющим активов:

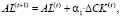(15)

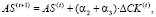
где доли α1, α2, α3 распределения собственных средств банка между активами совпадают с приведенными в соотношениях (14).

Баланс банка, связывающий временные интервалы t и t+1:

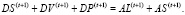(16)

Параметрическая модель оптимизации кредитно-инвестиционной деятельности коммерческого банка в динамическом варианте включает критерий (12) (на максимум), внутри шаговые ограничения (1)-(8), (13) и межпериодные ограничения (14)-(16). Состав эндогенных (управляемых) параметрами динамической модели расширен, по сравнению со статистическим вариантом, переменными α1, α2, α3.

Параметрическая модель оптимального банковского портфеля депозитов-кредитов может быть эффективно решена на двух уровнях. На первом решается задача оптимального управления портфелем для очередного временного интервала, на втором – задача мониторинга сформированного портфеля и выбора его параметров для очередного временного интервала с использованием динамической процедуры Р. Беллмана [4, 25].

Численные алгоритмы решения задач первого и второго уровня основываются на:

– методах и моделях аппроксимации нелинейных зависимостей (1), (2) спроса на депозиты, кредиты и инвестиции от объемов предложений и процентных ставок;

– методах и моделях оценки свободных для размещения в инвестиции средств коммерческого банка, представленных в работах Бурухановой Т.Д. [8] и Киселевой И.А. [3];

– моделях и численном методе нелинейной дискретной оптимизации, представленном в работе Халикова М.А. [26].

Оптимальный кредитный портфель банка ХХХ рассчитывался на даты: 31.10, 30.11, 31.12 2019 г. (таблица 5). Портфель диверсифицирован, однако основная сумма приходится на кредиты негосударственным и коммерческим организациям (юридическим лицам) на сроки от 181 дня до 1 года и от 1 года до 3 лет.

Портфель депозитов банка (таблица 6) состоит из средств, полученных от физических лиц: резидентов и нерезидентов. Основную долю вкладчиков составляют физические лица – резиденты, с позиции временной структуры преобладают депозиты сроком от 181 дня до 1 года и от 1 года до 3 лет.

В таблице 7 приведены значения ключевых показателей банковского портфеля: V(t), Y(t), P(t), k2(t) (объём кредитного портфеля, объём погашений по ранее размещённым кредитам, объём просроченной задолженности, коэффициент просроченной задолженности).

Таблица 7

Расчётные значения показателей V(t), Y(t), P(t) для банка ХХХ, млн. руб., %

Приведенные данные позволяют утверждать, что банк ХХХ контролирует риск банкротства заёмщика и поддерживает просроченную задолженность на уровне ниже порогового значения.

В таблице 8 представлены значения нормативов ликвидности для банка ХХХ на соответствующие даты. Из данных таблицы следует, что банк выполняет все нормативы ликвидности (Н2, Н3, Н4) в каждом из рассматриваемых периодов и обладает значительным запасом мгновенной и текущей ликвидности.

По результатам проведенных расчётов можно утверждать, что параметрическая модель оптимального управления кредитно-депозитным портфелем коммерческого банка даёт адекватную оценку корректности выбранной банком кредитно-инвестиционной политики и качества сформированного портфеля.

Заключение

Важной особенностью современной банковской практики является снижение доходности кредитно-инвестиционной деятельности в условиях сокращения розничного кредитования, роста кредитной задолженности и падения кредитоспособного спроса. Банки вынуждены повышать требования к ссудополучателям, а при формировании и управлении кредитно-депозитным портфелем использовать повышенные нормативы, устанавливаемые регулятором и рекомендованные международным банковским сообществом.

В этих условиях важное значение приобретает корректное определение внутренних банковских нормативов, регулирующих операционные и кредитные риски и влияющих на структуру и элементный состав банковского портфеля. Также весьма актуальной является проблема уточнения критерия оптимальности деятельности коммерческого банка на стратегическом горизонте планирования.

Эти и другие проблемы управления банковскими пассивами и активами могут быть решены с использованием параметрической модели банка, в рамках которой возможно ставить и решать задачу выбора оптимального соотношения регулируемых и нерегулируемых коммерческим банком параметров, используемых в критерии и ограничениях при формировании портфеля кредитов-депозитов.

В работе предложены варианты параметрической модели банка в статичном и динамическом вариантах. Модельные расчеты по этим моделям на данных выбранного коммерческого банка показали их адекватность поставленной задаче и возможность корректного использования в банковской практике при управлении портфелями депозитов-ссуд.

Библиографическая ссылка