Введение
Крупные интегрированные производственные структуры и вертикально-интегрированные холдинги занимают значительное место в экономике России и преобладающее – в добывающих и обрабатывающих отраслях, характеризующихся высокой концентрацией капитала и его неоднородностью по стоимости и риску. По этой причине, а также в силу институциональных несовершенств внутрифирменных механизмов управления производственной и инвестиционной сферами рыночной деятельности структурных подразделений холдингов актуальной и практически значимой становится задача повышения эффективности внутрифирменного кредитования. Трансфертное (внутрифирменное) кредитование-важный инструмент корпоративного управления, значимость которого усиливается в условиях снижения доступности и ограничений внешнего финансирования. Для современной экономики России – это практически единственный значимый резерв роста синергии объединения ранее независимых хозяйствующих субъектов в интегрированные группы предприятий (ИГП) и производственные холдинги [1, 5, 7, 8, 15, 17, 18].
Особенности внутрифирменного кредитования с учетом риска и уровня централизации внутрифирменных денежных потоков в рамках ИГП, характерные для российских условий становления и функционирования корпоративного бизнеса, достаточно подробно рассмотрены в работах зарубежных [6, 11] и отечественных исследователей [2, 3, 10, 13, 16, 19]. В цитируемых работах основное внимание уделено взаимосвязи риска и стоимости внутрифирменного кредитования с эффективностью производственной и инвестиционной деятельности подразделений холдинга, а также вопросам выбора оптимальной рыночной стратегии ИГП. Анализ перечисленных и других доступных авторам источников показал недостаточную разработанность проблематики повышения эффективности внутрифирменного кредитования в рамках ИГП и холдингов на основе корректного выбора приоритетной очереди структурных подразделений, претендующих на финансирование производственных программ и инвестиционных проектов из централизованных источников и, в том числе, общефирменного инвестиционного фонда.
Цель исследования – разработка инструментария моделей и методов выбора оптимального варианта внутрифирменного софинансирования инвестиционных программ структурных подразделений вертикально-интегрированного холдинга с учетом уровня централизации денежных и инвестиционных потоков и отдачи (рентабельности) общефирменного капитала в результатах их инвестиционной деятельности.
Результаты исследования и их обсуждение
1. Постановка задачи и математическая модель выбора оптимального варианта централизованного финансирования инвестиционных проектов структурных подразделений холдинга.
Выбранный в качестве основного и наиболее часто встречающийся на практике частично-децентрализованный вариант организационной структуры интегрированной группы предприятий (ИГП) предусматривает взаимную заинтересованность структурных подразделений и управляющей компании в результатах инвестиционной деятельности предприятий группы. Последние формируют инвестиционные программы и планируют инвестиционные затраты, которые покрываются собственным капиталом и трансфертными платежами из централизованного инвестиционного фонда (ЦИФ) ИГП, находящегося в распоряжении управляющей (материнской) компании. УК привлекает дополнительные средства сторонних инвесторов и, выступая в роли внутрифирменного инвестиционного банка, выделяет средства ЦИФа структурным подразделениям ИГП на платной основе, учитывая при согласовании ставки внутрифирменного кредита как «надежность» структурного подразделения во внутрифирменных платежах, так и приоритетность и рентабельность заявленных им инвестиционных проектов.
Представленная постановка задачи организации отбора инвестиционных программ подразделений ИГП и их финансирования в полной мере «укладывается» в схему задачи многоуровневой оптимизации.
Далее рассмотрим двухуровневую модель оптимального управления инвестиционной деятельностью интегрированной группы предприятий.
Верхний уровень – выбор инвестиционной стратегии управляющей компании.
Приведем перечень параметров и переменных модели верхнего уровня:
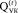 – объем ЦИФ ИГП на начало временного интервала t;
– объем ЦИФ ИГП на начало временного интервала t;
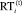 – объем заявки i-й СБЕ на централизованное (в рамках ЦИФ) финансирование технических и других проектов в интервале t;
– объем заявки i-й СБЕ на централизованное (в рамках ЦИФ) финансирование технических и других проектов в интервале t;
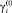 – ставка трансфертного (внутрифирменного) кредитования инвестиционных проектов i-й СБЕ в периоде t, выбранная на основе модели оптимальной стоимости внутрифирменного кредита и согласованная в рамках финансового взаимодействия УК и СБЕ в начале временного интервала;
– ставка трансфертного (внутрифирменного) кредитования инвестиционных проектов i-й СБЕ в периоде t, выбранная на основе модели оптимальной стоимости внутрифирменного кредита и согласованная в рамках финансового взаимодействия УК и СБЕ в начале временного интервала;
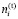 – номер i-й СБЕ
– номер i-й СБЕ 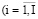 ) в приоритетной последовательности номеров СБЕ ИГП (построенной по принципу «от СБЕ с высоким приоритетом к СБЕ с низким приоритетом»), сформированной для шага t с использованием эвристического алгоритма, например, с синтетическим критерием Вальда-Сэвиджа, предложенного проф. Лабскером Л.Г. и приведенным в работе [9]. (В следующем разделе приведено описание численного алгоритма выбора приоритетной очереди структурных подразделений холдинга на предмет централизованного финансирования их инвестиционных проектов с позиции управляющей компании, а также представлен численный пример финансироваания проектов структурных подразделений вертикально-интегрированного холдинга);
) в приоритетной последовательности номеров СБЕ ИГП (построенной по принципу «от СБЕ с высоким приоритетом к СБЕ с низким приоритетом»), сформированной для шага t с использованием эвристического алгоритма, например, с синтетическим критерием Вальда-Сэвиджа, предложенного проф. Лабскером Л.Г. и приведенным в работе [9]. (В следующем разделе приведено описание численного алгоритма выбора приоритетной очереди структурных подразделений холдинга на предмет централизованного финансирования их инвестиционных проектов с позиции управляющей компании, а также представлен численный пример финансироваания проектов структурных подразделений вертикально-интегрированного холдинга);
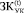 – максимальный объем внешнего (в том числе, заемного) финансирования инвестиционной деятельности подразделений ИГП для временного интервала t, определенный стратегией УК, условиями и ограничениями финансовых рынков;
– максимальный объем внешнего (в том числе, заемного) финансирования инвестиционной деятельности подразделений ИГП для временного интервала t, определенный стратегией УК, условиями и ограничениями финансовых рынков;
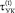 – средняя для временного интервала t ставка внешнего кредита для УК холдинга;
– средняя для временного интервала t ставка внешнего кредита для УК холдинга;
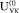 – планируемый для временного интервала t объем привлекаемого внешнего кредита (эндогенная (управляемая) переменная);
– планируемый для временного интервала t объем привлекаемого внешнего кредита (эндогенная (управляемая) переменная);
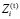 – планируемый объем трансфертных отчислений в интервале планирования t на финансирование инвестиционной деятельности i-й СБЕ (эндогенная (управляемая) переменная).
– планируемый объем трансфертных отчислений в интервале планирования t на финансирование инвестиционной деятельности i-й СБЕ (эндогенная (управляемая) переменная).
С учетом введенных обозначений модель верхнего уровня представлена следующими соотношениями:
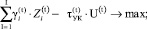 (1)
(1)
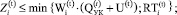 (2)
(2)
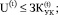 (3)
(3)
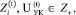 (4)
(4)
где 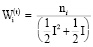 – коэффициент значимости i-й СБЕ в централизованном финансировании инвестиционной деятельности подразделений ИГП – модифицированный коэффициент Фишберна (15).
– коэффициент значимости i-й СБЕ в централизованном финансировании инвестиционной деятельности подразделений ИГП – модифицированный коэффициент Фишберна (15).
Учитывая, что ограничение (2) естественным образом преобразуется в два неравенства типа «≤», можно утверждать, что модель верхнего уровня (модель УК) относится к моделям линейного целочисленного программирования и может быть успешно решена одним из известных алгоритмов, например, методом «ветвей и границ».
Нижний уровень – выбор оптимального набора инвестиционных проектов i-й СБЕ 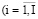 ), которые планируется реализовать в интервале времени t.
), которые планируется реализовать в интервале времени t.
Переменные и параметры модели нижнего уровня (секторной задачи для i-й СБЕ):
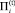 – набор инвестиционных проектов i-й СБЕ для временного интервала t с указанием для каждого l-го (l = 1,
– набор инвестиционных проектов i-й СБЕ для временного интервала t с указанием для каждого l-го (l = 1, 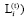 проекта совокупных затрат
проекта совокупных затрат 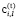 на его реализацию и ожидаемого по окончании временного интервала t эффекта
на его реализацию и ожидаемого по окончании временного интервала t эффекта 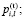
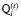 – объем собственного инвестиционного фонда i-й СБЕ на начало временного интервала t;
– объем собственного инвестиционного фонда i-й СБЕ на начало временного интервала t;
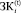 – максимальный для временного интервала t объем заемного финансирования инвестиционной деятельности i-й СБЕ из внешних источников;
– максимальный для временного интервала t объем заемного финансирования инвестиционной деятельности i-й СБЕ из внешних источников;
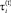 – средняя для временного интервала t ставка внешнего кредита для i-й СБЕ;
– средняя для временного интервала t ставка внешнего кредита для i-й СБЕ;
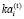 – пороговое для интервала t значение коэффициента автономии для i-й СБЕ, характеризующее риск структуры капитала ее инвестиционной сферы;
– пороговое для интервала t значение коэффициента автономии для i-й СБЕ, характеризующее риск структуры капитала ее инвестиционной сферы;
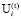 – планируемый для интервала t объем внешнего кредита для финансирования инвестиционной деятельности i-й СБЕ (эндогенная (управляемая) переменная);
– планируемый для интервала t объем внешнего кредита для финансирования инвестиционной деятельности i-й СБЕ (эндогенная (управляемая) переменная);
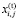 – булева переменная – признак включения/не включения j-го проекта в инвестиционную программу i-й СБЕ на временном интервале t.
– булева переменная – признак включения/не включения j-го проекта в инвестиционную программу i-й СБЕ на временном интервале t.
С учетом введенных обозначений модель секторной задачи (нижнего уровня) без учета производственно-технологических ограничений реализации инвестиционной программы i-й СБЕ задается следующими соотношениями:
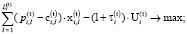 (5)
(5)
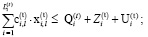 (6)
(6)
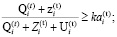 (7)
(7)
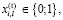
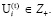 (8)
(8)
Учитывая, что ограничение (8) может быть представлено следующим линейным неравенством:
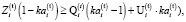 (9)
(9)
То делаем вывод – задача целочисленного программирования (5) – (8) имеет следующее тривиальное решение. При наличии значительного числа инвестиционных проектов все они будут включены в оптимальную инвестиционную программу i-й СБЕ в порядке убывания маржинальной доходности. При этом объем внешнего кредита достигнет максимальной величины, задаваемой ограничением (7) на структуру капитала инвестиционной сферы i-й СБЕ.
Ясно, что наличие тривиального решения задачи (5) – (8) связано с ее «рюкзачной» спецификой: причина в том, что постановка задачи нижнего уровня не учитывает некоторые важные особенности инвестиционной деятельности предприятий в составе ИГП, например, обеспечение рентабельности внутрифирменного кредитования для i-й СБЕ и для временного интервала t на уровне выше его доходности, задаваемой ставкой 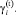
Таким образом, модель (5) – (8) задачи нижнего уровня следует дополнить следующим ограничением на минимальную рентабельность включаемых в инвестиционную программу i–й СБЕ проектов:
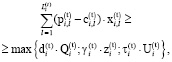 (10)
(10)
где 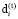 – средневзвешенная стоимость собственного капитала i-й СБЕ для временного интервала t.
– средневзвешенная стоимость собственного капитала i-й СБЕ для временного интервала t.
Включение в модель секторной задачи ограничения (10) позволяет обеспечить выбор инвестиционных проектов i-й СБЕ на шаге t, согласованный по объемам финансирования из собственных источников, внутрифирменных кредитов и внешних заимствований.
Модель (5) – (10), как легко видеть, относится к моделям линейного (ограничение (10) может быть представлено в форме трех линейных неравенств) целочисленного программирования, а решение соответствующей секторной задачи может быть получено одним из методов отсечений, например, «ветвей и границ».
2. Постановка задачи и численный алгоритм выбора приоритетной последовательности подразделений холдинга, претендующих на трансфертное (внутрифирменное) кредитование из средств централизованного инвестиционного фонда ИГП.
Для построения приоритетной последовательности подразделений холдинга предлагается провести их ранжирование по показателю рентабельность инвестиций на рубль общефирменного капитала. Процедуру ранжирования предлагается организовать на основе алгоритма игры с природой с использованием синтетического критерия Вальда-Сэвиджа, введенного в оборот Л. Лабскером (Лев Григорьевич Лабскер – профессор кафедры «Математическое моделирование экономических процессов» ФГОБУ ВПО «Финансовый университет при Правительстве РФ». Автор 165 научных и учебно-методических публикаций в области теории аппроксимации в банаховых пространствах, систем Чебышева, теории массового обслуживания и теории игр). Исходные данные численного примера взяты из бухгалтерской (финансовой) отчетности АО СУЭК за период с 2014 по 2018 г. СУЭК [4].
Синтетический критерий Вальда-Сэвиджа включает:
– критерий Вальда, позволяющий определить оптимальность стратегии с позиции выигрыша;
– критерий Сэвиджа, который позволяет выбрать стратегию с позиции игрового риска.
По критерию Вальда (W-оптимальной) оптимальной во множестве чистых стратегий является стратегия, которая обеспечивает W-максимальный среди минимальных выигрышей. Оптимальное решение, выбранное данным образом, исключает риск и гарантирует, что полученный результат, в каком бы состоянии не находилась «природа», не достигает значение ниже W. Критерий Вальда также называется «принципом гарантированного результата» (критерий «крайнего пессимизма относительно выигрышей») [9, с. 115-117] и применяют в тех случаях, когда целью субъекта является не выигрыш, а желание не проиграть.
По критерию Сэвиджа (S-оптимальной) оптимальной во множестве чистых стратегий является стратегия, которая обеспечивает S-минимальный среди максимальных рисков. Этот критерий также определяют, как «критерий крайнего пессимизма» и применяются в случаях, когда ЛПР (лицо, принимающее решение) при выборе стратегии ориентируется на наибольший риск – «природа» находится в наихудшем для игрока состоянии [9, с. 125-126].
Линейная комбинация критериев позволит подойти к выбору оптимальной с позиции выигрыша и риска стратегии управляющей компании.
Для описания синтетического критерия введем коэффициенты, которые характеризуют степень предпочтения управляющей компании выигрыша и риска: r∈[0, 1] и (1 – r). Выбор численного значения показателя r является субъективным и зависит от требуемой ожидаемой доходности и толерантности к риску [9, с. 138].
Критерий Вальда-Сэвиджа с выигрыш-показателем r∈[0, 1] определим по формуле:
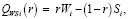 (11)
(11)
где Wi – показатель эффективности стратегии Ai по критерию Вальда; Si – показатель эффективности стратегии Ai по критерию Сэвиджа, i∈I.
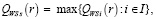 (12)
(12)
где QWs(r) – цена игры в чистых стратегиях.
Назовем оптимальной стратегию Af на множестве s чистых стратегий при условии, что:
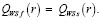 (13)
(13)
Множество QWS(r)-оптимальных на множестве s чистых стратегий обозначим как 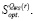
В цитируемой работе Л.Г. Лабскера доказано, что каждая стратегия, которая оптимальна на множестве s чистых стратегий по критерию Вальда-Сэвиджа, является оптимальной на множестве s как по критерию Вальда, так и по критерию Сэвиджа. Кроме того, при r∈(0, 1) структура множества 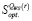 стратегий, оптимальных на множестве чистых стратегий по критерию Вальда-Сэвиджа с выигрыш-коэффициентом r, не зависит от значений r∈(0, 1) [9, с. 147-155].
стратегий, оптимальных на множестве чистых стратегий по критерию Вальда-Сэвиджа с выигрыш-коэффициентом r, не зависит от значений r∈(0, 1) [9, с. 147-155].
Для применения вышеизложенной модели воспользуемся алгоритмом Л. Лабскера, который нами был усовершенствован исходя из целей работы.
Для использования синтетического критерия Вальда-Сэвиджа необходимо определить показатель сравнительной оценки СБЕ при формировании их приоритетной с позиции УК очереди. В качестве такого показателя предлагается использовать рентабельность инвестиций в капитал СБЕ на рубль общефирменного капитала.
Алгоритм:
1. Сформировать матрицу A выигрышей, элементами которой будут показатели рентабельности инвестиций на руб. общефирменного капитала за период с 2014 г. по 2018 г.;
2. Используя формулу (14) найти по данным матрицы А показатели эффективности Wi стратегий Ai, i∈I, по критерию Вальда [9, с. 115]:
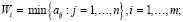 (14)
(14)
3. По найденным в п. 2 показателям Wi, 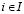 , найти по формуле (15) цену игры Ws в чистых стратегиях по критерию Вальда [9, с. 115]:
, найти по формуле (15) цену игры Ws в чистых стратегиях по критерию Вальда [9, с. 115]:
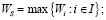 (15)
(15)
4. Используя п.п. 2 и 3, определить множество стратегий 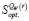 , оптимальных во множестве чистых стратегий по критерию Вальда;
, оптимальных во множестве чистых стратегий по критерию Вальда;
5. Используя матрицу А, сформировать матрицу рисков R;
6. По данным матрицы R вычислить показатели Si стратегий Ai, i∈I по критерию Сэвиджа;
7. По найденным в п. 6 показателям Si, i∈I, по формуле (16) найти цену игры по критерию Сэвиджа в чистых стратегиях, Ss [9, с.131]:
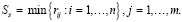 (16)
(16)
8. Используя п.п. 6 и 7, определить множество стратегий 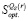 , оптимальных во множестве чистых стратегий по критерию Сэвиджа.
, оптимальных во множестве чистых стратегий по критерию Сэвиджа.
9. По данным п.п. 4 и 8 проверить выполнимость условия [9, с. 156]:
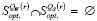 ;
;
Если данное условие не выполняется, то множество стратегий 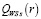 , оптимальных на множестве S, имеет структуру [9, с. 152]:
, оптимальных на множестве S, имеет структуру [9, с. 152]:
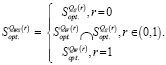 (17)
(17)
Если условие выполняется, то перейти к следующему пункту;
10. По данным п.п. 4 и 6 найти цену игры 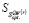 в стратегиях множества
в стратегиях множества 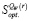 по критерию Сэвиджа;
по критерию Сэвиджа;
11. По данным п.п. 3 и 8 найти цену игры 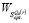 в стратегиях множества
в стратегиях множества 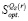 по критерию Вальда;
по критерию Вальда;
12. По данным п.п. 4 и 8 определить множество стратегий, не являющихся оптимальными на множестве чистых стратегий ни по критерию Вальда, ни по критерию Сэвиджа;
13. Для каждой стратегии, определенной в п. 12, с использованием пунктов 3, 7, 10, 11 проверить справедливость неравенства [9, с. 163]:
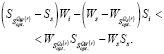 (18)
(18)
Если хотя бы для одной стратегии данное неравенство не выполняется, то алгоритм завершается и о структуре 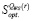 нельзя сказать ничего определенного.
нельзя сказать ничего определенного.
Если же для каждой стратегии неравенство выполняется, переходим к следующему пункту;
14. По данным п.п. 3 и 8 определить множество 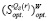 , оптимальных на
, оптимальных на 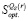 по критерию Вальда;
по критерию Вальда;
15. По данным п.п. 4 и 6 определить множество 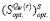 , оптимальных на
, оптимальных на 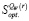 по критерию Сэвиджа;
по критерию Сэвиджа;
16. По данным п.п. 3, 7, 10, 11 рассчитать значение 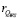 по формуле (19) [9, с. 157]:
по формуле (19) [9, с. 157]:
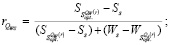 (19)
(19)
17. По данным п.п. 4, 8, 14, 15, 16 по формуле (20) [9, с. 165] определить структуру множества оптимальных чистых стратегий 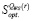 :
:
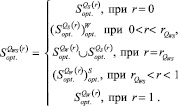 (20)
(20)
Численный пример рейтингования структурных подразделений холдинга по приоритету финансирования их инвестиционной деятельности из централизованного инвестиционного фонда холдинга проведем на основе информационной базы АО «Сибирская угольная энергетическая компания».
СУЭК – одна из крупнейших угольных компаний мира, а также ведущий производитель угля и энергии в России [12]. Компания поставляет уголь в 48 стран через собственную развитую сбытовую сеть и включает 22 основных подразделений: ООО «Арктические разработки», ООО «Черновские ЦЭММ», ООО «Читауголь», АО «Разрез Харанорский», АО «СУЭК-Кузбасс», ООО «Сибнииуглеобогащение», ООО «Объединенное ПТУ Кузбасса», АО «Разрез Березовский», АО «Разрез Назаровский», ООО «Гринфин», ООО «Бородинский РМЗ», АО «ШУ Восточное», ООО «Правобережное», АО «Разрез Тугнуйский», ООО «Тугнуйская обогатительная фабрика», ООО «Тугнуйское ПТУ», ООО «СУЭК-Хакасия», АО «Разрез Изыхский», ООО «Восточно-Бейский разрез», АО «Черногорский ремонтно-механический завод», АО «Ургалуголь», АО «Дальтрансуголь». НЕиже в работе используется 14 подразделений, по которым удалось получить финансово-экономические данные за период с 2014 г. по 2018 г. [4].
Таким образом, компания имеет возможность одновременного финансирования инвестиционной деятельности нескольких своих дочерних компаний, что и актуализирует задачу выбора их приоритетной последовательности.
Приоритетная последовательность структурных подразделений в планах трансфертного кредитования, как указано выше, организована на основе показателя отдачи на руб. инвестиций материнской компании.
Ниже в табл. 1 и 2 представлены величины трансфертных отчислений и премий (млн руб.) по каждому предприятию холдинга за период с 2014 г. по 2018 г.
Основой для применения алгоритма Л. Лабскера и критерия Вальда-Сэвиджа являются данные табл. 3 – матрицы выигрышей, включающей показатели рентабельности инвестиций из централизованного фонда в предприятия холдинга (отдача на руб. общефирменного капитала).
В последнем столбце матрицы выигрышей рассчитаны показатели эффективности Wi, i = 1,2,…,14 стратегий Аi, i = 1,2,…,14, по критерию Вальда. В последней строке – показатели благоприятности βj, i = 1,2,…,5, состояний природы Пj, i = 1,2,…,5.
Таблица 1
Объемы трансфертов по предприятиям АО «СУЭК» (млн руб.)*
|
2018 |
2017 |
2016 |
2015 |
2014 |
|
|
ООО «Арктические разработки» |
704,8 |
696,4 |
703,6 |
191,2 |
187 |
|
ООО «Черновские ЦЭММ» |
24,8 |
9,6 |
5 |
10,8 |
7,6 |
|
АО «Разрез Харанорский» |
20 |
2,8 |
1,4 |
20,6 |
21,4 |
|
АО «СУЭК-Кузбасс» |
1350,2 |
120,6 |
43,2 |
58,4 |
9,8 |
|
ООО «Сибнииуглеобогащение» |
41 |
41,6 |
40,4 |
38,6 |
39,6 |
|
АО «Разрез Березовский» |
1,8 |
4,6 |
3 |
4,2 |
5 |
|
АО «Разрез Назаровский» |
2,8 |
6,8 |
3,8 |
5 |
6,2 |
|
ООО «Бородинский РМЗ» |
2,2 |
1,6 |
3,4 |
5,6 |
2,8 |
|
АО «Разрез Тугнуйский» |
1963 |
23,6 |
5,6 |
4,8 |
6 |
|
ООО «Тугнуйская обогатительная фабрика» |
1,2 |
20 |
50 |
110 |
110 |
|
ООО «СУЭК-Хакасия» |
372,4 |
19,6 |
9,2 |
8,8 |
8 |
|
АО «Разрез Изыхский» |
1 |
2,4 |
1,4 |
1,6 |
1 |
|
АО «Ургалуголь» |
3785,6 |
1794,2 |
279 |
10 |
1,6 |
|
АО «Дальтрансуголь» |
15,4 |
14,2 |
8,2 |
9,6 |
8,8 |
Примечание. *– таблица составлена авторами с использованием источника [4].
Таблица 2
Премии УК, перечисленные предприятиями АО «СУЭК» (млн руб.)*
|
2018 |
2017 |
2016 |
2015 |
2014 |
|
|
ООО «Арктические разработки» |
968 |
1139 |
153 |
-243 |
707 |
|
ООО «Черновские ЦЭММ» |
165 |
115 |
73 |
12 |
12 |
|
АО «Разрез Харанорский» |
2240 |
1866 |
1888 |
1616 |
1545 |
|
АО «СУЭК-Кузбасс» |
97108 |
87218 |
60810 |
31495 |
32276 |
|
ООО «Сибнииуглеобогащение» |
210 |
215 |
199 |
181 |
64 |
|
АО «Разрез Березовский» |
2122 |
1917 |
2068 |
2704 |
2533 |
|
АО «Разрез Назаровский» |
1752 |
1675 |
1075 |
1312 |
1585 |
|
ООО «Бородинский РМЗ» |
166 |
183 |
114 |
55 |
82 |
|
АО «Разрез Тугнуйский» |
29624 |
22513 |
20615 |
13821 |
12994 |
|
ООО «Тугнуйская обогатительная фабрика» |
1787 |
1949 |
621 |
109 |
361 |
|
ООО «СУЭК-Хакасия» |
14677 |
11111 |
11903 |
11659 |
9275 |
|
АО «Разрез Изыхский» |
2257 |
1785 |
1253 |
1353 |
992 |
|
АО «Ургалуголь» |
6529 |
5447 |
2683 |
959 |
1566 |
|
АО «Дальтрансуголь» |
5353 |
5320 |
5243 |
5085 |
5085 |
Примечание. *– таблица составлена авторами с использованием источника [4].
Таблица 3
Матрица выигрышей по показателю «Рентабельность инвестиций в СБЕ, входящих в организационную структуру АО «СУЭК»
|
Матрица выигрышей |
2018 |
2017 |
2016 |
2015 |
2014 |
Wi |
|
ООО «Арктические разработки» |
1,373 |
1,636 |
0,217 |
-1,271 |
3,781 |
-1,27092 |
|
ООО «Черновские ЦЭММ» |
6,653 |
11,979 |
14,600 |
1,111 |
1,579 |
1,111111 |
|
АО «Разрез Харанорский» |
112,000 |
666,429 |
1348,571 |
78,447 |
72,196 |
72,19626 |
|
АО «СУЭК-Кузбасс» |
71,921 |
723,201 |
1407,639 |
539,298 |
3293,469 |
71,9212 |
|
ООО «Сибнииуглеобогащение» |
5,122 |
5,168 |
4,926 |
4,689 |
1,616 |
1,616162 |
|
АО «Разрез Березовский» |
1178,889 |
416,739 |
689,333 |
643,810 |
506,600 |
416,7391 |
|
Окончание табл. 3 |
||||||
|
Матрица выигрышей |
2018 |
2017 |
2016 |
2015 |
2014 |
Wi |
|
АО «Разрез Назаровский» |
625,714 |
246,324 |
282,895 |
262,400 |
255,645 |
246,3235 |
|
ООО «Бородинский РМЗ» |
75,455 |
114,375 |
33,529 |
9,821 |
29,286 |
9,821429 |
|
АО «Разрез Тугнуйский» |
15,091 |
953,941 |
3681,250 |
2879,375 |
2165,667 |
15,09119 |
|
ООО «Тугнуйская обогатительная фабрика» |
1489,167 |
97,450 |
12,420 |
0,991 |
3,282 |
0,990909 |
|
ООО «СУЭК-Хакасия» |
39,412 |
566,888 |
1293,804 |
1324,886 |
1159,375 |
39,41192 |
|
АО «Разрез Изыхский» |
2257,000 |
743,750 |
895,000 |
845,625 |
992,000 |
743,75 |
|
АО «Ургалуголь» |
1,725 |
3,036 |
9,616 |
95,900 |
978,750 |
1,724694 |
|
АО «Дальтрансуголь» |
347,597 |
374,648 |
639,390 |
529,688 |
577,841 |
347,5974 |
|
βj |
2257 |
953,940678 |
3681,25 |
2879,375 |
3293,4694 |
Ws = 743,75 |
Таблица 4
Матрица рисков централизованного финансирования инвестиционных программ АО «СУЭК»
|
Матрица выигрышей |
2018 |
2017 |
2016 |
2015 |
2014 |
Si |
|
ООО «Арктические разработки» |
2255,6266 |
952,305124 |
3681,03255 |
2880,6459 |
3289,68864 |
3681,033 |
|
ООО «Черновские ЦЭММ» |
2250,3468 |
941,961511 |
3666,65 |
2878,2639 |
3291,89044 |
3666,65 |
|
АО «Разрез Харанорский» |
2145 |
287,512107 |
2332,67857 |
2800,9284 |
3221,27313 |
3221,273 |
|
АО «СУЭК-Кузбасс» |
2185,0788 |
230,740015 |
2273,61111 |
2340,0771 |
0 |
2340,077 |
|
ООО «Сибнииуглеобогащение» |
2251,878 |
948,772409 |
3676,32426 |
2874,6859 |
3291,85323 |
3676,324 |
|
АО «Разрез Березовский» |
1078,1111 |
537,201548 |
2991,91667 |
2235,5655 |
2786,86939 |
2991,917 |
|
АО «Разрез Назаровский» |
1631,2857 |
707,617149 |
3398,35526 |
2616,975 |
3037,82423 |
3398,355 |
|
ООО «Бородинский РМЗ» |
2181,5455 |
839,565678 |
3647,72059 |
2869,5536 |
3264,18367 |
3647,721 |
|
АО «Разрез Тугнуйский» |
2241,9088 |
0 |
0 |
0 |
1127,80272 |
2241,909 |
|
ООО «Тугнуйская обогатительная фабрика» |
767,83333 |
856,490678 |
3668,83 |
2878,3841 |
3290,18757 |
3668,83 |
|
ООО «СУЭК-Хакасия» |
2217,5881 |
387,052923 |
2387,44565 |
1554,4886 |
2134,09439 |
2387,446 |
|
АО «Разрез Изыхский» |
0 |
210,190678 |
2786,25 |
2033,75 |
2301,46939 |
2786,25 |
|
АО «Ургалуголь» |
2255,2753 |
950,904785 |
3671,63351 |
2783,475 |
2314,71939 |
3671,634 |
|
АО «Дальтрансуголь» |
1909,4026 |
579,292791 |
3041,85976 |
2349,6875 |
2715,62848 |
3041,86 |
Определим структуру множества 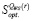 стратегий, оптимальных во множестве чистых стратегий по синтетическому критерию Вальда-Сэвиджа, по вышеизложенному алгоритму.
стратегий, оптимальных во множестве чистых стратегий по синтетическому критерию Вальда-Сэвиджа, по вышеизложенному алгоритму.
Показатели эффективности стратегий по критерию Вальда представлены в последнем столбце таблицы 3. Цена игры в чистых стратегиях по критерию Вальда: Ws = 743,75.
Из последнего столбца следует, что W12 = Ws = 743,75. Поэтому стратегия А12 оптимальна по критерию Вальда, а, следовательно, 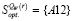 . Напомним, что под стратегией понимается выбор приоритетной с позиции внутрифирменного кредитования очереди структурных подразделений. Например, стратегия А12 означает приоритетное финансирование в АО «Разрес Изыхский».
. Напомним, что под стратегией понимается выбор приоритетной с позиции внутрифирменного кредитования очереди структурных подразделений. Например, стратегия А12 означает приоритетное финансирование в АО «Разрес Изыхский».
Составим матрицу рисков (таблица 4).
Показатели рассчитаны и представлены в последнем столбце таблицы 4. Цена игры по критерию Сэвиджа Ss = 2241,909. Множество стратегий 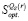 , оптимальных во множестве чистых стратегий по критерию Сэвиджа, состоит из одной стратегии А9, следовательно,
, оптимальных во множестве чистых стратегий по критерию Сэвиджа, состоит из одной стратегии А9, следовательно, 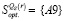 .
.
Используя данные из таблиц 3 и 4, по формуле (10) рассчитаем значение критерия для каждой стратегии на концах отрезка [0, 1] и полученные результаты представим в таблице 5:
Таблица 5
Показатель эффективности на концах отрезка [0, 1]
|
i |
Qwsi(0) = -Si |
Qwsi(1) = Wi |
|
1 |
-3681,03255 |
-1,270920502 |
|
2 |
-3666,65 |
1,111111111 |
|
3 |
-3221,27313 |
72,19626168 |
|
4 |
-2340,07705 |
71,92119686 |
|
5 |
-3676,32426 |
1,616161616 |
|
6 |
-2991,91667 |
416,7391304 |
|
7 |
-3398,35526 |
246,3235294 |
|
8 |
-3647,72059 |
9,821428571 |
|
9 |
-2241,90881 |
15,09118696 |
|
10 |
-3668,83 |
0,990909091 |
|
11 |
-2387,44565 |
39,41192266 |
|
12 |
-2786,25 |
743,75 |
|
13 |
-3671,63351 |
1,724693576 |
|
14 |
-3041,85976 |
347,5974026 |
Из полученных результатов следует: левый конец 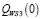 отрезка
отрезка 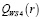 стратегии А3, меньше показателя в левом конце стратегии А4, А9, А11; правый конец
стратегии А3, меньше показателя в левом конце стратегии А4, А9, А11; правый конец 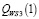 стратегии А3 больше правых концов стратегий А4, А9, А11. Таким образом, можно установить взаимные пересечения отрезков
стратегии А3 больше правых концов стратегий А4, А9, А11. Таким образом, можно установить взаимные пересечения отрезков 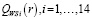 , которые наглядно представлены в таблице 6.
, которые наглядно представлены в таблице 6.
Таблица 6
Пересечения отрезков 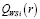
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
|
1 |
||||||||||||||
|
2 |
||||||||||||||
|
3 |
x |
x |
x |
|||||||||||
|
4 |
x |
x |
x |
x |
||||||||||
|
5 |
x |
|||||||||||||
|
6 |
x |
x |
x |
|||||||||||
|
7 |
||||||||||||||
|
8 |
||||||||||||||
|
9 |
x |
x |
x |
x |
||||||||||
|
10 |
x |
|||||||||||||
|
11 |
x |
x |
x |
|||||||||||
|
12 |
||||||||||||||
|
13 |
||||||||||||||
|
14 |
x |
x |
x |
Отметка «х» означает пересечение отрезков. Далее найдем значения r на пересечении каждого отрезка, решая уравнение 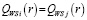 . Получим следующие значения r для каждого пересечения: r34 = 0,99968; r39 = 0,9449; r311 = 0,96216; r46 = 0,654; r49 = 0,63335; r414 = 0,71796; r510 = 0,92299; r69 = 0,65124; r611 = 0,615677; r914 = 0,70638; r1114 = 0,67984.
. Получим следующие значения r для каждого пересечения: r34 = 0,99968; r39 = 0,9449; r311 = 0,96216; r46 = 0,654; r49 = 0,63335; r414 = 0,71796; r510 = 0,92299; r69 = 0,65124; r611 = 0,615677; r914 = 0,70638; r1114 = 0,67984.
Значения показателя эффективности 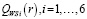 при значениях r = 0, r34, r39, r311, r46, r49, r414, r510, r69, r611, r914, r1114 1 и номера стратегий в приоритетной последовательности для различных r представим в таблице 7.
при значениях r = 0, r34, r39, r311, r46, r49, r414, r510, r69, r611, r914, r1114 1 и номера стратегий в приоритетной последовательности для различных r представим в таблице 7.
Таблица 7
Определение приоритетной последовательности подразделений АО «СУЭК» по критерию Вальда-Сэвиджа
|
Показатели эффективности Qwsi (r)чистых стратегий Ai |
|||||||
|
значение показателя r |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
0 |
-3681 |
-3666,7 |
-3221,3 |
-2340,1 |
-3676,3 |
-2991,9 |
-3398,4 |
|
14 |
10 |
7 |
2 |
13 |
5 |
8 |
|
|
0 < r < 0,616 |
14 |
10 |
7 |
2 |
13 |
5 |
8 |
|
0,615677438 |
-1415,5 |
-1408,5 |
-1193,6 |
-855,06 |
-1411,9 |
-893,28 |
-1154,4 |
|
14 |
10 |
8 |
3 |
13 |
5 |
7 |
|
|
0,616 < r < 0,633 |
14 |
10 |
8 |
3 |
13 |
5 |
7 |
|
0,633350639 |
-1350,5 |
-1343,7 |
-1135,4 |
-812,44 |
-1346,9 |
-833,04 |
-1090 |
|
14 |
10 |
8 |
2,5 |
13 |
4 |
7 |
|
|
0,633 < r < 0,651 |
14 |
10 |
8 |
2 |
13 |
4 |
7 |
|
0,651243067 |
-1284,6 |
-1278 |
-1076,4 |
-769,28 |
-1281,1 |
-772,05 |
-1024,8 |
|
14 |
10 |
8 |
2 |
13 |
3 |
7 |
|
|
Окончание табл. 7 |
|||||||
|
Показатели эффективности Qwsi (r)чистых стратегий Ai |
|||||||
|
значение показателя r |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
0,651 < r < 0,654 |
14 |
10 |
8 |
2 |
13 |
3 |
7 |
|
0,654025663 |
-1274,4 |
-1267,8 |
-1067,3 |
-762,57 |
-1270,9 |
-762,57 |
-1014,6 |
|
14 |
10 |
8 |
3 |
13 |
2 |
7 |
|
|
0,654 < r < 0,680 |
14 |
10 |
8 |
3 |
13 |
2 |
7 |
|
0,679840418 |
-1179,4 |
-1173,2 |
-982,24 |
-700,3 |
-1175,9 |
-674,57 |
-920,56 |
|
14 |
10 |
8 |
3 |
13 |
2 |
7 |
|
|
0,680 < r < 0,706 |
14 |
10 |
8 |
3 |
13 |
2 |
7 |
|
0,70638517 |
-1081,7 |
-1075,8 |
-894,82 |
-636,28 |
-1078,3 |
-584,09 |
-823,81 |
|
14 |
10 |
8 |
3 |
13 |
2 |
7 |
|
|
0,706 < r < 0,718 |
14 |
10 |
8 |
3 |
13 |
2 |
7 |
|
0,71796645 |
-1039,1 |
-1033,3 |
-856,67 |
-608,34 |
-1035,7 |
-544,62 |
-781,6 |
|
14 |
10 |
8 |
3,5 |
13 |
2 |
7 |
|
|
0,718 < r < 0,923 |
14 |
10 |
8 |
3 |
13 |
2 |
7 |
|
0,92299381 |
-284,64 |
-281,33 |
-181,42 |
-113,82 |
-281,61 |
154,25 |
-34,339 |
|
14 |
11 |
8 |
5 |
13 |
2 |
4 |
|
|
0,923 < r < 1 |
14 |
11 |
8 |
5 |
13 |
2 |
4 |
|
1 |
-1,2709 |
1,11 |
72,196 |
71,92 |
1,6161 |
416,73 |
246,324 |
|
14 |
12 |
5 |
6 |
11 |
2 |
4 |
|
|
Показатели эффективности Qwsi (r)чистых стратегий Ai |
|||||||
|
значение показателя r |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
0 |
-3647,7 |
-2241,9 |
-3668,8 |
-2387,4 |
-2786,3 |
-3671,6 |
-3041,9 |
|
9 |
1 |
11 |
3 |
4 |
12 |
6 |
|
|
0 < r < 0,616 |
9 |
1 |
11 |
3 |
4 |
12 |
6 |
|
0,615677438 |
-1395,9 |
-852,32 |
-1409,4 |
-893,28 |
-612,91 |
-1410 |
-955,05 |
|
9 |
2 |
11 |
4 |
1 |
12 |
6 |
|
|
0,616 < r < 0,633 |
9 |
2 |
11 |
4 |
1 |
12 |
6 |
|
0,633350639 |
-1331,2 |
-812,44 |
-1344,5 |
-850,39 |
-550,52 |
-1345,1 |
-895,14 |
|
9 |
2,5 |
11 |
5 |
1 |
12 |
6 |
|
|
0,633 < r < 0,651 |
9 |
3 |
11 |
5 |
1 |
12 |
6 |
|
0,651243067 |
-1265,8 |
-772,05 |
-1278,9 |
-806,97 |
-487,36 |
-1279,4 |
-834,5 |
|
9 |
4 |
11 |
5 |
1 |
12 |
6 |
|
|
0,651 < r < 0,654 |
9 |
4 |
11 |
5 |
1 |
12 |
6 |
|
0,654025663 |
-1255,6 |
-765,77 |
-1268,7 |
-800,22 |
-477,54 |
-1269,2 |
-825,07 |
|
9 |
4 |
11 |
5 |
1 |
12 |
6 |
|
|
0,654 < r < 0,680 |
9 |
4 |
11 |
5 |
1 |
12 |
6 |
|
0,679840418 |
-1161,2 |
-707,51 |
-1173,9 |
-737,57 |
-386,41 |
-1174,3 |
-737,57 |
|
9 |
4 |
11 |
5 |
1 |
12 |
6 |
|
|
0,680 < r < 0,706 |
9 |
4 |
11 |
5 |
1 |
12 |
6 |
|
0,70638517 |
-1064,1 |
-647,6 |
-1076,5 |
-673,15 |
-292,71 |
-1076,8 |
-647,6 |
|
9 |
4 |
11 |
6 |
1 |
12 |
5 |
|
|
0,706 < r < 0,718 |
9 |
4 |
11 |
6 |
1 |
12 |
5 |
|
0,71796645 |
-1021,7 |
-621,46 |
-1034 |
-645,04 |
-251,83 |
-1034,3 |
-608,34 |
|
9 |
5 |
11 |
6 |
1 |
12 |
3,5 |
|
|
0,718 < r < 0,923 |
9 |
5 |
11 |
6 |
1 |
12 |
4 |
|
0,92299381 |
-271,83 |
-158,71 |
-281,61 |
-147,47 |
471,91 |
-281,15 |
86,5882 |
|
9 |
7 |
12 |
6 |
1 |
10 |
3 |
|
|
0,923 < r < 1 |
9 |
7 |
12 |
6 |
1 |
10 |
3 |
|
1 |
9,82143 |
15,0912 |
0,99091 |
39,411 |
743,75 |
1,72469 |
347,597 |
|
9 |
8 |
13 |
7 |
1 |
10 |
3 |
|
Таким образом для каждой последовательности рассчитаны показатели эффективности, которые далее ранжированы в невозрастающем порядке. Каждому значению присвоен порядковый номер (в таблице 7 номера проставлены под показателями эффективности).
В случае, если номера некоторых показателей эффективности в одной строке совпадают, то для соответствующих стратегий номера в приоритетной последовательности можно менять.
Если ищется номер чистой стратегии в приоритетной последовательности для r, находящемся в некотором интервале, то стратегии будет присвоен номер места в приоритетной последовательности, общий для концов этого интервала. Например, для стратегии А1 общим порядковым номером места в приоритетной последовательности является номер 14 при значении выигрыш-показателя на концах интервала (0,923;1). Следовательно, при любом значении r из данного интервала стратегия А1 займет 14 место.
На основе проведенных расчетов получена следующая приоритетная последовательность подразделений АО «СУЭК» – объектов централизованного финансирования инвестиционной деятельности, которую следует учитывать при выборе внутрифирменной стратегии управляющей компании: АО «Разрез Изыхский, АО «Разрез Березовский, АО «Дальтрансуголь», АО «Разрез Назаровский, АО «Разрез Харанорский», АО «СУЭК-Кузбасс, ООО «СУЭК-Хакасия, АО «Разрез Тугнуйский», ООО «Бородинский РМЗ», АО «Ургалуголь», ООО «Сибнииуглеобогащение, ООО «Черновские ЦЭММ», ООО «Тугнуйская обогатительная фабрика», ООО «Арктические разработки».
Заключение и выводы
В статье представлен оригинальный комплекс экономико-математических моделей и методов многоуровневой оптимизации инвестиционной деятельности структурных подразделений вертикально-интегрированного холдинга с частично-децентрализованной организационной структурой. Основное внимание авторы уделили методологии выбора приоритетной очереди заявок на трансфертное кредитование инвестиционных проектов подразделений из централизованного фонда холдинга. Предложено для этой и подобных задач внутрифирменного планирования и управления использовать инструментальные средства «игр с природой» и, в том числе, алгоритмы ранжирования, построенные на основе синтетического критерия Вальда-Сэвиджа.
Результаты верификации разработанных моделей и численных методов на объектах АО «СУЭК» подтвердили их соответствие сформулированной цели исследования и перспективы использования в практической деятельности крупных производственных предприятий корпоративного сектора российской экономики.
Библиографическая ссылка
Анохина П.Н., Беляева Д.И., Димитриев А.М., Максимов Д.А. ОПТИМИЗАЦИЯ ВНУТРИФИРМЕННОГО КРЕДИТОВАНИЯ ПОДРАЗДЕЛЕНИЙ ИЕРАРХИЧЕСКОЙ ПРОИЗВОДСТВЕННОЙ СТРУКТУРЫ С КРИТЕРИЯМИ ИГРЫ С ПРИРОДОЙ // Вестник Алтайской академии экономики и права. 2020. № 1-1. С. 4-16;URL: https://vaael.ru/ru/article/view?id=933 (дата обращения: 03.02.2026).
DOI: https://doi.org/10.17513/vaael.933

