Научный журнал

Вестник Алтайской академии экономики и права

Print ISSN 1818-4057

Online ISSN 2226-3977

Перечень ВАК

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Корсакова Е.А. 1

---

1 ФГБОУ ВО «Уральский государственный экономический университет»

Цель данного исследования заключается в определении количественной связи между темпами прироста валового внутреннего продукта России, темпами прироста объема основного капитала и темпами прироста эффективности его использования, в оценке вклада, который вносят в прирост валового внутреннего продукта эти факторы. Для достижения этой цели в данном исследовании было применено уравнение разработанной Г.А. Фельдманом модели экономического роста, которое описывает количественную связь между темпами прироста народного дохода, темпами прироста объема основных и оборотных фондов, а также темпами прироста эффективности их использования. Материалами для исследования послужили данные Росстата о динамике валовой добавленной стоимости, физического объема основного капитала и фондоотдачи. Проведенное исследование выявило наличие тесной и стабильной связи между динамикой роста валовой добавленной стоимости, физического объема основного капитала и фондоотдачи, а также позволило оценить вклад в прирост валового внутреннего продукта экстенсивных и интенсивных факторов экономического роста. Изучение количественной зависимости между темпами прироста этих макроэкономических показателей открывает возможности для прогнозирования и анализа влияния различных факторов на темпы роста валового внутреннего продукта и их устойчивость.

Статья в формате PDF

1255 KB

темпы прироста

валовой внутренний продукт

валовая добавленная стоимость

основной капитал

эффективность использования основного капитала

фондоотдача

1. Harrod R. F. An Essay in Dynamic Theory // The Economic Journal. 1939. Vol. 49. Is. 193. P. 14–33. DOI: 10.2307/2225181.

2. Domar E. Essays in the Theory of Economic Growth. New York: Oxford University Press, 1957. URL: https://ia803206.us.archive.org/28/items/in.ernet.dli.2015.228950/2015.228950 (дата обращения: 15.03.2025).

3. Полетаев А.В. К вопросу о российском вкладе в мировую экономическую науку // Национальная гуманитарная наука в мировом контексте: опыт России и Польши: сб. / под ред.: Е. Аксер, И.М. Савельева. М.: Издательский дом ГУ–ВШЭ, 2010. 368 с. ISBN 978-5-7598-0676-9.

4. Фельдман М.А. «Предвосхитившие работу, выполненную западными экономистами», или феномен журнала «Плановое хозяйство» // Вопросы теоретической экономики. 2021. № 1. С. 112–120. URL: https://cyberleninka.ru/article/n/predvoshitivshie-rabotu-vypolnennuyu-zapadnymi-ekonomistami-ili-fenomen-zhurnala-planovoe-hozyaystvo. (дата обращения: 15.03.2025). DOI: 10.24411/2587-7666-2020-10109.

5. Фельдман Г.А. К теории темпов народного дохода (Под углом зрения народного хозяйства СССР) // Плановое хозяйство. 1928. № 11. С. 146–170. [Электронный ресурс]. URL: https://istmat.org/files/uploads/43951/g.a.feldman.k_teorii_tempov_narodnogo_dohoda.pdf (дата обращения: 20.03.2025).

6. Золотухин А.А. Теория роста на основе трудовой теории стоимости // AlterEconomics. 2022. Т. 19. № 2. С. 306-325. DOI: 10.31063/AlterEconomics/2022.19-2.6.

7. Ляховецкий А.М., Петренко А.П., Маханбетова А.Д. Статистический анализ обеспеченности и использования основных фондов // Естественно-гуманитарные исследования. 2024. № 3(53). С. 224–227. URL: https://cyberleninka.ru/article/n/statisticheskiy-analiz-obespechennosti-i-ispolzovaniya-osnovnyh-fondov. EDN: SUJIIU.

8. Синявская Е.Е., Синявская В.В. Состояние и эффективность использования основных фондов Краснодарского края // Естественно-гуманитарные исследования. 2023. № 4 (48). С. 318–325. URL: https://cyberleninka.ru/article/n/sostoyanie-i-effektivnost-ispolzovaniya-osnovnyh-fondov-krasnodarskogo-kraya/viewer (дата обращения: 15.03.2025). EDN: QTQEOR.

9. Корсакова Е.А. Сущность и показатели устойчивого экономического роста: региональный аспект // Вестник Алтайской академии экономики и права. 2022. № 11-3. С. 458-463. DOI: 10.17513/vaael.2590.

10. Буданов И.А. Инвестирование как процесс накопления основного капитала страны // Научные труды: Институт народнохозяйственного прогнозирования РАН. Т. 21. № 4. С. 23–47. DOI: 10.47711/2076-3182-2023-4-23-47.

11. Сухарев О.С. Инвестиции в экономический рост и структурную трансформацию России // Финансы: теория и практика. 2025 Т. 29. № 2. С. 181-193. DOI: 10.26794/2587-5671-2025-29-2-181-193.

12. Сухарев О.С., Ворончихина Е.Н. Структурная динамика экономики: влияние инвестиций в старые и новые технологии // Экономические и социальные перемены: факты, тенденции, прогноз. 2020. Т. 13. № 4. С. 74–90. DOI: 10.15838/esc.2020.4.70.4.

13. Салин В.Н., Ситникова О.Ю., Третьякова О.Г., Шпаковская Е.П. Анализ и управление инвестициями // Управленческие науки. 2023. № 13(2). С. 109–120. DOI: 10.26794/2304-022X 2023-13-2-109-120.

14. Куклинова П.С. Анализ подходов к оценке эффективности денежно-кредитной политики // Экономика и бизнес: теория и практика. 2023. № 10-2 (104). С. 28-30. DOI: 10.24412/2411-0450-2023-10-2-28-30.15.

15. Кириякова Н.И. Взаимосвязь денежного и реального секторов экономики, влияние ключевой ставки Банка России // Вестник Алтайской академии экономики и права. 2023. № 9. С. 54–59. DOI: 10.17513/vaael.2972.

Введение

Проблема темпов экономического роста является одной из ключевых проблем макроэкономики. В XX веке экономисты активно разрабатывали модели, с помощью которых можно было выявить основные факторы, способствующие экономическому росту. Они стремились определить условия, при которых возможно достижение высоких и устойчивых темпов роста экономики. Исследователи экономической динамики искали способы достижения стабильных темпов экономического роста. Для этого нужно было прежде всего выяснить, как количественно связаны между собой темпы роста валового внутреннего продукта с макроэкономическими показателями, характеризующими динамику факторов предложения экономического роста. Большинство современных моделей экономического роста исходят из того, что основными факторами роста являются факторы предложения, т. е. труд и капитал. Со времен А. Смита в экономической науке экономический рост рассматривается как результат процесса накопления капитала.

Развитию современной макроэкономической теории роста, согласно точке зрения представителей зарубежной экономической мысли, положила начало публикация в 1939 году сторонником кейнсианской теории английским экономистом Harrod R.F. статьи «Очерк теории динамики», в которой он связывал темп прироста валового выпуска с нормой накопления и отдачей, производительностью капитала, которая рассматривалась им как постоянная величина [1].

Одна из моделей определения темпов прироста была разработана американским экономистом E. Domar. Описание этой модели было представлено им в книге «Очерки по теории экономического роста», опубликованной в 1957 году. В модели E. Domar темп прироста валового выпуска определяется темпом прироста инвестиций, а последний зависит от предельной производительности капитала и предельной склонности к сбережению [2].

E. Domar обратил внимание на сходство предложенной им модели экономического роста с моделью, разработанной советским экономистом Г.А. Фельдманом в 1928 году [3]. В главе IX «Советская модель роста» E. Domar изложил суть модели экономического роста, разработанной Г.А. Фельдманом. При этом он подчеркнул, что эта советская модель более разработана, чем аналогичные модели, созданные на Западе [2, p. 17]. Таким образом, приоритет в построении первой макроэкономической модели экономического роста и характеристике основных условий для устойчивого и постоянного роста экономики принадлежит Г.А. Фельдману [4, с. 114].

Исследование факторов, определяющих темпы прироста валового внутреннего продукта, а также оценка их вклада в прирост валового внутреннего продукта остается важной проблемой современной макроэкономической теории и в XXI веке. Особую актуальность эта проблема приобретает в современных условиях, когда в России идет поиск путей достижения высоких и устойчивых темпов экономического роста.

Цель исследования заключается в выявлении с помощью модели экономического роста Г.А. Фельдмана количественной связи между темпами прироста валового внутреннего продукта России, темпами прироста объема основного капитала и темпами прироста эффективности его использования, а также в оценке вклада, который вносят в прирост валового внутреннего продукта эти факторы.

Материалы и методы исследования

В основе исследования лежат основные идеи теории экономического роста. В процессе исследования были использованы различные научные методы, включая анализ, синтез и сравнение, а также статистические методы, в частности корреляционно-регрессионный анализ.

В ходе исследования на основе модели экономического роста, разработанной Г.А. Фельдманом, была изучена связь между изменениями валовой добавленной стоимости, объёма основного капитала и эффективности его использования. В качестве исходных данных были использованы данные Росстата о динамике валовой добавленной стоимости, объёма основного капитала и эффективности его использования.

Результаты исследования и их обсуждение

Проблема темпов экономического роста в экономической теории и хозяйственной практике была сформулирована в СССР ещё в 20-ые годы XX века в связи с разработкой текущих и перспективных планов развития народного хозяйства. В этот период была поставлена задача научного обоснования темпов экономического роста и факторов, его определяющих. Решению этой задачи была посвящена статья Г.А. Фельдмана «К теории темпов народного дохода», опубликованная в журнале «Плановое хозяйство» в 1928 году [5, с. 146–170]. Он пытался выяснить зависимость темпов роста народного дохода от объема капитала и эффективности его использования. В модели Г.А. Фельдмана процесс экономического роста, его динамизм, т. е. темпы прироста валового выпуска непосредственно связаны с процессом увеличения объема основного капитала, или с процессом инвестирования, а также с эффективностью использования основного капитала [6, с. 308].

Г.А. Фельдман представил в этой статье основные уравнения динамики своей модели экономического роста. С помощью этих уравнений он продемонстрировал, какие экономические переменные определяют динамику народного дохода, планируемые темпы его роста. По его мнению, главные факторы, от которых зависят темпы роста народного дохода, являются объем основного капитала и эффективность его использования (капиталоотдача или фондоотдача).

«Народный доход» Г.А. Фельдман рассматривал как всю вновь созданную стоимость в условиях расширенного воспроизводства [5, с. 154]. Это понятие совпадает с современным понятием «валовая добавленная стоимость» или произведенным валовым внутренним продуктом. Под эффективностью использования капитала он понимал отношение всей вновь созданной стоимости за определенный период времени, т. е. народного дохода, к стоимости основных и оборотных капиталов за этот же период, т. е. фондоотдачу (формула 1) [5, с. 151]. Фондоотдача показывает буквально какой объем произведенного валового внутреннего продукта или валовой добавленной стоимости приходится на 1 рубль фондов:

С = НД / К, (1)

где С – эффективность использования капиталов;

НД – вновь созданная стоимость (народный доход);

К – стоимость основных и оборотных капиталов.

Из этой формулы следует, что величина народного дохода зависит от размеров применяемого капитала и эффективности его использования (НД = С ×К).

Понятие «темп роста» совпадает у Г.А. Фельдмана с понятием «темп прироста». Темп роста Г.А. Фельдман рассматривал как отношение прироста за единицу времени к растущей величине [5, с. 155]. Таким образом, под темпами роста Г.А. Фельдман понимал буквально темпы прироста. Поэтому далее автор использовал понятие «темп прироста». С точки зрения математики темп прироста представляет собой отношение первой производной функции к функции или производную логарифма функции. Темп прироста народного дохода (Т) может быть рассчитан по формуле 2 [5, с. 155]:

Т = ΔНД / НД =

= (dНД / dt) × (1 / НД) = dlnНД / dt, (2)

где Т – темп прироста народного дохода или вновь созданной стоимости;

ΔНД – абсолютное изменение, абсолютный прирост вновь созданной стоимости (народного дохода) за единицу времени;

НД – предыдущее значение объема вновь созданной стоимости (народного дохода).

Темпы прироста основных и оборотных капиталов определяются аналогично по формуле 3:

Гк = ΔК / К = (dК / dt) × (1 / К) = dlnК / dt, (3)

где Гк – темп прироста основных и оборотных капиталов;

ΔК – абсолютное изменение, абсолютный прирост объема основных и оборотных капиталов за единицу времени;

К – предыдущее значение объема основных и оборотных капиталов.

Темп прироста эффективности использования капиталов рассчитывается соответственно по формуле 4:

Гс = ΔС / С = (dС / dt) × (1 / С) = dlnС / dt, (4)

где ΔС / С – темп прироста эффективности использования основных и оборотных капиталов;

ΔС – абсолютное изменение, абсолютный прирост эффективности использования основных и оборотных капиталов за единицу времени;

С – предыдущее значение эффективности использования основных и оборотных капиталов.

Используя сформулированные им определения темпов прироста народного дохода, капиталов и эффективности их использования, Г.А. Фельдман вывел следующую формулу темпов прироста народного дохода (формула 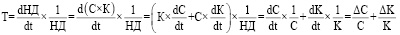5):

, (5)

где Т – темп прироста народного дохода или вновь созданной стоимости;

ΔС / С – темп прироста эффективности использования основных и оборотных капиталов;

ΔК / К – темп прироста основных и оборотных капиталов;

Таблица 1

Динамика валовой добавленной стоимости, объема основных фондов и фондоотдачи

Примечание: составлено и рассчитано автором; индекс изменения фондоотдачи рассчитывается как частное от деления индекса физического объема добавленной стоимости года t к году (t-1) на индекс физического объема основных фондов года t к году (t-1) в сопоставимых ценах.

Источник: Росстат / Статистика / Официальная статистика / Национальные счета / Валовой внутренний продукт / Произведенный ВВП. URL: https://rosstat.gov.ru/statistics/accounts; Российский статистический ежегодник. 2024: Стат. сб./Росстат. М., 2024. 304 с. [Электронный ресурс]. URL: https://rosstat.gov.ru/storage/mediabank/Ejegodnik_2024.pdf.

Таблица 2

Расчет темпов прироста валовой добавленной стоимости

Примечание: рассчитано автором по данным таблицы 1.

Из этого уравнения следует, что темп прироста народного дохода или валовой добавленной стоимости равен сумме темпов прироста объёма капитала и эффективности его использования [5, с. 156]. Это уравнение показывает, что темпы прироста валовой добавленной стоимости зависят от двух факторов, а именно, от темпов прироста объема капитала, связанного с накоплением капитала, величиной чистых инвестиций, направляемых на увеличение объема капитала, а также от темпов прироста эффективности его использования, т. е. фондоотдачи. Другими словами, темпы прироста валовой добавленной стоимости фактически предопределяются темпами прироста капитала и эффективности его использования, т. е. фондоотдачи [5, с. 157].

Данное уравнение было использовано для определения составляющих темпов прироста валовой добавленной стоимости в России на основе данных, представленных в таблице 1.

По данным таблицы 1, в которой представлена динамика валовой добавленной стоимости, объема основного капитала и фондоотдачи, с помощью уравнения Г.А. Фельдмана были рассчитаны темпы прироста валовой добавленной стоимости в России за 2014–2023 гг., которые оказались довольно близки к фактическим темпам прироста (таблица 2).

Таблица 3

Сравнение фактических и расчетных темпов прироста валовой добавленной стоимости

Примечание: рассчитано автором по данным таблиц 1 и 2.

Таблица 4

Основные результаты регрессионного анализа

Примечание: рассчитано автором по данным таблиц 1 и 2.

Данные таблицы 3 свидетельствуют о наличии значительного соответствия расчетных и фактических темпов прироста валовой добавленной стоимости. Коэффициент корреляции между этими двумя величинами составляет 0,78. Это означает, что между фактическим и расчетными показателями темпов прироста валового внутреннего продукта существует значительная положительная корреляция. Поэтому модель, предложенную Г.А. Фельдманом, можно считать моделью, максимально приближенной к действительности. Данная модель может быть использована для прогнозирования и анализа влияния различных факторов на темпы прироста валового внутреннего продукта и их устойчивость.

С целью определения силы влияния темпов прироста объема основного капитала и темпов прироста фондоотдачи, как показателя эффективности его использования, на темпы прироста валовой добавленной стоимости был проведен регрессионный анализ данных, представленных в таблицах 1 и 2 (таблица 4).

По результатам данного анализа можно сделать следующие выводы. Значение R-квадрат показывает, что изменение темпов прироста валовой добавленной стоимости можно на 99,9% объяснить изменениями, происходящими в темпах прироста объема основного капитала и эффективности его использования. Поскольку R-квадрат > 0,95, то это означает, что используемая модель хорошо описывает исследуемые взаимосвязи. Положительные коэффициенты при переменных, которыми являются темпы прироста объема основного капитала и фондоотдачи, свидетельствуют о наличии прямой связи между темпами прироста объема добавленной стоимости (зависимой переменной) и независимыми переменными модели. Величина показателей «значимость F» и «P-значение» наглядно демонстрирует статистическую значимость модели.

Высокое значение коэффициента детерминации R-квадрат (0,99) может свидетельствовать о наличии мультиколлинеарности, когда между независимыми переменными в модели существует сильная корреляция. Рассчитанный по данным таблицы 2 коэффициент корреляции между темпами прироста фондоотдачи и темпами прироста объема основного капитала составляет 0,15. Следовательно, высокое значение коэффициента детерминации в данной регрессионной модели объясняется оптимальным набором независимых переменных для предсказания зависимой переменной в уравнении Г.А. Фельдмана. Поскольку данная модель используется для прогнозирования, а не для точного определения и интерпретации коэффициентов, то даже наличие мультиколлинеарности может не иметь существенного негативного влияния. Основное внимание в данном исследовании уделялось общей объяснительной силе и предсказательной способности модели.

За анализируемый период наблюдались положительные темпы прироста объема основного капитала, но при этом снижалась эффективность его использования, т. е. снижение фондоотдачи. Согласно результатам регрессионного анализа, темпы прироста фондоотдачи оказывают более сильное влияние на темпы прироста валовой добавленной стоимости, чем темпы прироста объема основного капитала. Об этом свидетельствует величина соответствующих коэффициентов, полученных в результате проведенного регрессионного анализа. Коэффициент при переменной X1 (темпы прироста объема основного капитала) равен 0,91, а при переменной X2 (темпы прироста фондоотдачи) составляет 1,03. Поэтому для достижения высоких и устойчивых темпов прироста валовой добавленной стоимости необходимо повышение фондоотдачи, т. е. объема произведенной продукции на 1 рубль стоимости основного капитала. Это будет означать, что каждый рубль, вложенный в основной капитал, приносит все больший объем валовой добавленной стоимости [7, с. 225]. Другими словами, растет эффективность его использования, а экономический рост достигается за счет более полного использования интенсивных факторов роста. Эффективное использование основного капитала позволяет снизить издержки производства, увеличить темпы роста производимого продукта. Повышение эффективности использования основного капитала, что выражается в росте фондоотдачи, выступает как важный фактор интенсивного роста экономики [8, с. 324].

Влияние темпов прироста объема основного капитала на темпы прироста валовой добавленной стоимости и их устойчивость также значительно [9, с. 458]. Накопления капитала представляет собой увеличение объема основных фондов. Процессы, связанные с динамикой основных фондов в России, по данным Росстата, представляются исключительно стабильными [10, с. 24]. Реальное увеличение объема основного капитала происходит за счет роста объема чистых инвестиций. Эмпирический анализ экономического роста в России в период 2000–2023 гг. подтверждает, что темп роста определяется динамикой инвестиций [11, с. 181]. При этом наибольший вклад в рост экономики вносят инвестиции в технологическое обновление [12, с. 74]. Объем основного капитала в экономике сокращается на величину выбытия (амортизации), поэтому для увеличения его объема необходимо, чтобы объем валовых инвестиций превышал объем восстановительных инвестиций, компенсирующих выбытие основного капитала. Инвестиционные ресурсы являются ведущим фактором развития экономики, обеспечивающим устойчивые темпы ее роста. Однако, в современных условиях темпы увеличения объема инвестиций в основной капитал недостаточны для того, чтобы оказывать значительное воздействие на развитие экономики [13, с. 110]. Темпы прироста физического объема капитала зависят во многом от инвестиционной политики. Достижение устойчивого экономического роста на основе устойчивого роста инвестиций в основной капитал может быть достигнуто с помощью денежно-кредитной политики [14, с. 28]. Особое влияние на процесс достижения устойчивого развития экономики России оказывает такой инструмент денежно-кредитной политики, как ключевая ставка [15, с. 54].

Заключение

В результате проведенного исследования с использованием уравнения модели экономического роста Г.А. Фельдмана было продемонстрировано наличие очень тесной и устойчивой связи между темпами прироста валовой добавленной стоимости, темпами прироста объема основных фондов и эффективностью их использования, т. е. фондоотдачи. Увеличение объема основного капитала или основных фондов относится к экстенсивным факторам экономического роста, а рост эффективности использования, т. е. рост фондоотдачи представляет собой интенсивный фактор экономического роста. Поэтому определение доли темпов прироста объема основных фондов и темпов прироста фондоотдачи в общей сумме темпов прироста валовой добавленной стоимости позволяет оценить вклад экстенсивных и интенсивных факторов экономического роста.

За исследуемый период в большинстве случаев наблюдалось снижение фондоотдачи. Прирост объема валовой добавленной стоимости в этих случаях достигался за счет прироста объема основного капитала, т. е. за счет экстенсивного фактора экономического роста. Устойчивость темпов прироста объема основного капитала зависит от устойчивости темпов прироста чистых инвестиций. В связи с этим особую актуальность приобретает совершенствование инструментов инвестиционной политики.

Для устойчивого роста фондоотдачи, т.е. эффективности использования основного капитала, относящейся к интенсивным факторам экономического роста необходимо, чтобы рост физического объема валовой добавленной стоимости опережал рост физического объема основного капитала. Основными направлениями повышения фондоотдачи в современных условиях является увеличение доли активной части основных фондов, т. е. более производительных машин и оборудования, в их общем объеме в результате технического перевооружения, снижение стоимости вновь вводимого оборудования на единицу его производственной мощности, повышение коэффициента сменности работы оборудования, ускоренное освоение вновь вводимых мощностей.

Библиографическая ссылка