Введение
Российская экономика представляет собой сложную систему, в которую входят предприятия более 70-ти отраслей. Очевидно, что формирование модели ее стратегического развития в соответствии с традиционным отраслевым подходом заранее обречено на серьезные трудности из-за необходимости учета чрезмерно большой совокупности разнонаправленных факторов, которые оказывают непосредственное воздействие на функционирование предприятий разных отраслей. Для упрощения подхода к решению этой задачи целесообразно использовать системный подход, что позволит выделить по функциональному признаку ведущие сектора экономики, а также значительно сократить размерность моделируемой системы до ряда моделей стратегий импортозамещения и развития указанных секторов [3, с. 807]. Эффективное формирование моделей стратегий импортозамещения и развития ведущих секторов экономики представляется возможным на основе использования существующих методов экономико-математического моделирования и их представления в качестве детерминированных и/или стохастических систем.
Основная цель данного исследования заключается в обосновании возможности применения существующих методов экономико-математического моделирования для разработки моделей стратегий импортозамещения и развития ведущих секторов российской экономики на основе учета их функциональных особенностей и представления в качестве детерминированных и/или стохастических систем.
Материал и методы исследования
В состав ведущих секторов российской экономики входит достаточно большое число хозяйствующих субъектов, многие из которых обладают рядом специфических особенностей. Именно наличие таких особенностей позволяет достаточно четко определить принадлежность того или иного хозяйствующего субъекта к одному из ведущих секторов российской экономики. Для подавляющего большинства хозяйствующих субъектов указанные особенности выражаются в функциональных принципах организации производства. На практике они проявляются в том, что в зависимости от рода и условий организации и ведения производственно-хозяйственной деятельности их учет при моделировании стратегий импортозамещения и развития ведущих секторов позволяет отнести некоторые из них к детерминированным, а другие – к стохастическим системам [5, с. 82].
Покажем особенности моделирования стратегий импортозамещения и развития ведущих секторов российской экономики в том случае, когда их можно отнести к детерминированным системам.
Детерминированной принято считать такую систему, будущее состояние которой можно точно прогнозировать на основе информации о ее текущем состоянии. Связи между входом u(t,x) и выходом y(t,x) таких систем описываются при помощи оператора θ, свойства которого во времени либо не меняются, либо эти изменения точно известны. В простейшем случае детерминированную систему можно представить в следующем виде:
y(t,x) = θ u(t,x). (1)
При этом функции входных u(t,x) и выходных y(t,x) параметров системы считаются известными, а детерминированный оператор θ остается неизвестным.
В случае моделирования стратегий импортозамещения и развития ведущих секторов российской экономики как детерминированной системы (1) формируется вспомогательная модель со входом u(t,x) и выходом y(t,x), которая характеризуется оператором 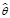 . Эту модель представим в виде следующего уравнения:
. Эту модель представим в виде следующего уравнения:
y(t,x) = 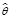 u(t,x). (2)
u(t,x). (2)
Задача моделирования детерминированной системы (1) будет заключаться в определении значения оператора 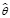 при соблюдении условия максимальной близости выходных параметров подсистемы y(t,x) и ее модели y(t,x). Различие между величинами этих параметров характеризует показатель их разности (невязки, ошибки), который можно выразить следующим уравнением:
при соблюдении условия максимальной близости выходных параметров подсистемы y(t,x) и ее модели y(t,x). Различие между величинами этих параметров характеризует показатель их разности (невязки, ошибки), который можно выразить следующим уравнением:
ε(t,x) = y(t,x) – y(t,x). (3)
Невязка ε(t,x) является функцией времени и пространственной координаты моделируемой системы. При этом каждый из ее аргументов определен на соответствующих ограниченных множествах: Т – интервал времени; X – множество локализации пространственных координат системы. Таким образом, невязка характеризует близость выходных параметров системы и ее модели в любой момент времени из интервала Т и в каждой точке множества локализации пространственных координат X.
Для количественной оценки близости могут использоваться некоторые числовые характеристики 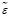 невязки ε, а именно: максимальная невязка (4), интегральная абсолютная невязка (5) и интегральная квадратичная невязка (6) [1, c. 79]. Формулы для определения этих характеристик приведены ниже:
невязки ε, а именно: максимальная невязка (4), интегральная абсолютная невязка (5) и интегральная квадратичная невязка (6) [1, c. 79]. Формулы для определения этих характеристик приведены ниже:
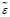 (
(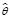 ) = εmax = max ε(t,x), t∈T, x∈X. (4)
) = εmax = max ε(t,x), t∈T, x∈X. (4)
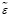 (
(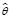 ) = εabc =
) = εabc =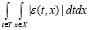 . (5)
. (5)
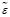 (
(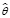 ) = εsqr =
) = εsqr =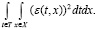 (6)
(6)
Выбрав одну из приведенных выше характеристик для оценки близости выходных параметров системы и ее модели, можно получить количественную оценку качества модели или, другими словами, количественную меру соответствия оператора модели 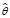 оператору системы q. Это дает возможность подбирать операторы для формирования модели стратегий импортозамещения и развития ведущих секторов российской экономики с целью уменьшения расчетных значений оценки ее близости по сравнению с моделируемой детерминированной системой. В результате приведенных выше рассуждений и проведения соответствующих преобразований можно утверждать, что под моделью стратегий импортозамещения и развития ведущего сектора экономики как детерминированной системы следует понимать модель с детерминированным оператором
оператору системы q. Это дает возможность подбирать операторы для формирования модели стратегий импортозамещения и развития ведущих секторов российской экономики с целью уменьшения расчетных значений оценки ее близости по сравнению с моделируемой детерминированной системой. В результате приведенных выше рассуждений и проведения соответствующих преобразований можно утверждать, что под моделью стратегий импортозамещения и развития ведущего сектора экономики как детерминированной системы следует понимать модель с детерминированным оператором 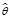 *, в которой минимизировано расчетное значение оценки близости выходных параметров системы и ее модели, то есть min
*, в которой минимизировано расчетное значение оценки близости выходных параметров системы и ее модели, то есть min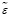 (
(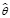 ).
).
Для формирования алгоритма решения такого рода задачи обычно задается класс операторов модели с точностью до конечной совокупности неизвестных параметров. С математической точки зрения это равнозначно параметризации оператора 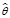 . Это означает, что данный оператор должен быть представлен некоторым набором неизвестных, но числовых параметров.
. Это означает, что данный оператор должен быть представлен некоторым набором неизвестных, но числовых параметров.
Для параметризованного оператора введем обозначение 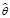 (W), где под W будем понимать вектор параметров. Если в параметризованном операторе выделить элементарные операторы и указать связи между ними, то данные параметры можно считать характеристиками этих связей. При параметризованных операторах невязки становятся функциями параметров W, то есть
(W), где под W будем понимать вектор параметров. Если в параметризованном операторе выделить элементарные операторы и указать связи между ними, то данные параметры можно считать характеристиками этих связей. При параметризованных операторах невязки становятся функциями параметров W, то есть 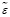 (W).
(W).
После параметризации оператора модели задача моделирования детерминированной подсистемы сводится к определению параметров W* оператора модели 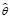 таким образом, чтобы
таким образом, чтобы
W* = arg min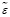 (W). (7)
(W). (7)
Покажем особенности моделирования стратегий импортозамещения и развития ведущих секторов российской экономики в том случае, если их можно отнести к стохастическим системам.
Основная отличительная характеристика стохастической системы заключается в том, что ее состояние в конкретный момент времени может определять ее будущее состояние только с некоторой степенью вероятности [2, с. 85]. Соответственно, выходные параметры такой системы будут представлять собой случайный процесс yω(t,x). Из этого вытекает принципиальное отличие стохастической системы от детерминированной, которое заключается в том, что связь между входными и выходными параметрами такой системы описывается стохастическим оператором qw:
yω(t,x) = qωu(t,x). (8)
Стохастический оператор можно рассматривать как совокупность S детерминированных операторов, каждый из которых реализуется с определенной вероятностью, где под ω будем понимать номер конкретного детерминированного оператора в этой совокупности.
Существуют два класса реализации операторов из совокупности S в интервале времени Т [4, c. 144].
Для первого класса детерминированные операторы, реализующиеся с вероятностью р, сохраняют свои свойства на всем интервале времени Т. В качестве самого простого примера этого класса реализации может выступать конечный пронумерованный набор детерминированных операторов q1,…, qs, а ω – представляет собой случайную целочисленную величину, которая принимает значения в интервале [1,s] с определенной функцией распределения вероятностей Р(ω).
Для второго класса детерминированные операторы из совокупности S могут реализовываться в произвольный момент времени на всем интервале Т. В этом случае ω будет представлять собой случайную функцию ω(m,h) со значениями из интервала [1,s] и функцией распределения вероятностей Р(ω (m_h),…, w(m0 ,h)).
Для моделирования стратегии импортозамещения и развития ведущего сектора российской экономики как стохастической системы (8) сформируем вспомогательную подсистему со стохастическим оператором 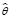 ω:
ω:
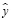 ω(t,x) =
ω(t,x) = 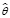 ω u(t,x). (9)
ω u(t,x). (9)
В дальнейшем приходим к заключению, что расчетное значение показателя невязки между выходными параметрами стохастической системы и ее модели становится так же случайным процессом:
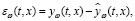 (10)
(10)
где ω является либо случайной функцией, либо случайной величиной.
Соответственно случайными величинами становятся и расчетные значения показателей оценки близости выходных параметров системы и ее модели (8)-(9). Поэтому для получения количественной оценки близости выходных параметров подсистемы и ее модели используются числовые характеристики соответствующих случайных величин. Обычно для этого достаточно использовать их средние значения. Другими словами, вместо максимальной, интегральной абсолютной и интегральной квадратичной оценок невязок будет использоваться следующая совокупность оценок: средняя максимальная невязка (11), средняя интегральная абсолютная невязка (12), средняя интегральная квадратичная невязка (13). Формулы для их определения приведены ниже [6, c. 176]:
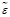 = εmax= M
= εmax= M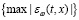 , t∈T, x∈X .(11)
, t∈T, x∈X .(11)
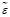 = ε abs = M
= ε abs = M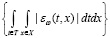 .(12)
.(12)
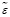 = ε sqr = M
= ε sqr = M 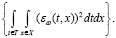 (13)
(13)
В выражениях (11)-(13) символ М означает операцию математического ожидания. В дальнейшем процесс формирования модели для стохастической подсистемы аналогичен рассмотренному выше процессу формирования модели для детерминированной системы. Разница будет заключаться только в том, что минимальное расчетное значение показателя невязки будет определяться среди стохастических операторов выбранного класса. При этом любой выбранный класс операторов должен быть описан в параметризованном виде. Однако, в отличие от детерминированной подсистемы, параметры W рассматриваются как случайные величины, которые характеризуются соответствующими функциями распределения вероятностей p(W,β). Вид функций распределения вероятностей обычно устанавливается на основе качественной априорной информации, а их параметры β (средние значения, дисперсии, высшие моменты) образуют группу неслучайных параметров модели стохастического оператора модели. Они определяются из следующего выражения:
β* = arg min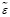 (β), (14)
(β), (14)
где средние невязки будут определяться из выражений (11)-(13).
Случайные параметры модели стохастической подсистемы генерируются с помощью источников случайных чисел и законами распределения вероятностей p(W,β*).
Результаты исследования и их обсуждение
Полученные нами результаты позволяют сделать вывод о том, что в процессе проведения исследований были выявлены особенности моделирования стратегий импортозамещения и развития ведущих секторов российской экономики как детерминированных и стохастических систем и обоснована необходимость их учета функциональных особенностей ведущих секторов российской экономики при моделировании стратегий их развития.
Выводы
Полученные в ходе проведения исследований результаты показывают, что при формировании стратегий импортозамещения и развития ведущих секторов российской экономики вполне применимы такие виды существующего информационно-аналитического инструментария как моделирование детерминированных и стохастических систем. Вместе с учетом функциональных особенностей организации и ведения производственно-хозяйственной деятельности хозяйствующими субъектами ведущих секторов этот инструментарий может использоваться и для оценки разработанных моделей стратегий импортозамещения и развития ведущих секторов российской экономики по минимизации расчетных значений показателей невязки.
Благодарности
Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований, проект № 17-06-00029а «Оценка эффективности стратегий развития ведущих секторов российской экономики в условиях санкций при помощи инструментария информационно-аналитического моделирования».
Библиографическая ссылка
Знаменская А.Н., Ларин С.Н., Стебеняева Т.В. ИНСТРУМЕНТАРИЙ ИНФОРМАЦИОННО-АНАЛИТИЧЕСКОГО МОДЕЛИРОВАНИЯ СТРАТЕГИЙ ИМПОРТОЗАМЕЩЕНИЯ И РАЗВИТИЯ ВЕДУЩИХ СЕКТОРОВ РОССИЙСКОЙ ЭКОНОМИКИ // Вестник Алтайской академии экономики и права. 2019. № 3-2. С. 72-76;URL: https://vaael.ru/ru/article/view?id=374 (дата обращения: 11.03.2026).
DOI: https://doi.org/10.17513/vaael.374

