Введение
При определении места расположения центра распределения необходимо учитывать возможные ограничения. Как минимум область, на которой производится решение, должна обладать разветвленной сетью дорог с целью организации транспортного взаимодействия. Также необходимо учитывать особенности регионального законодательства, учитывать ограничения по грузоподъемности, технические характеристики дорожного полотна и т.п. Все эти факторы в конечном счете определят возможность расположения распределительного центра с учет влияния случайных компонент в окрестности. Подобные задачи возникают во многих областях логистики. Особенное значение они имеют в транспортной логистике, управлении цепями поставок, а также в задачах планирования, моделях экономических систем [1,2].
Цель исследования – предложить поправки к алгоритму нахождения координат месторасположения распределительного центра относительно набора поставщиков ресурсов с учетом случайной составляющей.
Материалы и методы исследования
Существует достаточно много способов решения задач различных областей логистики. Решаются транспортные задачи, задачи логистики, связанные с оптимизацией материальных потоков и другие [3]. Сама по себе задача определения местоположение распределительного центра также имеет свое прикладное значение и в приложениях обычно решается геометрическим методов определения центра масс [5].
Общая постановка задачи определить координаты «центра масс» для вероятного, возможного размещения распределительного центра. Общий алгоритм подобного поиска состоит из шагов:
1) Строим многоугольник, в который увязывают точки, в которые необходимо организовать поставку из распределительного центра (рис. 1). Определяем координаты вершин многоугольника в привязке к масштабу конкретной карты, фрагмента карты.
2) В случае необходимости перестроить полученный многоугольник, включив любой резервный объект и рассчитать новый «центр масс».
3) Определить возможность организации распределительного центра (РЦ), склада в радиусе определенного центра масс.
4) Построить окрестности полученных точек, для этого необходимо в окрестности разместить вероятные координаты резервных точек. В этих точках могут быть размещены резервные объекты, планируемые объекты, центры распределения или потребители ресурсов.
5) Этот пункт алгоритма призван учесть случайную природу координат точек, которые анализируются в рамках задачи. Более подробно он будет представлен далее.
Приведем пример расположение на плоскости многоугольника, вершинами которого являются объекты, относительно которых необходимо определить координаты распределительного центра (рис. 1).
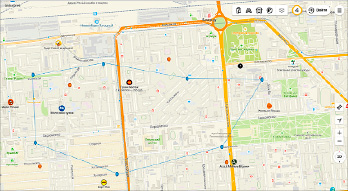
Рис. 1. Многоугольник с вершинами поставщиков ресурсов в привязке к условному фрагменту карты
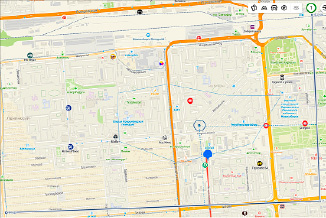
Рис. 2. Многоугольник с вершинами поставщиков ресурсов в привязке к условному фрагменту карты и системе координат с заранее выбранным масштабом
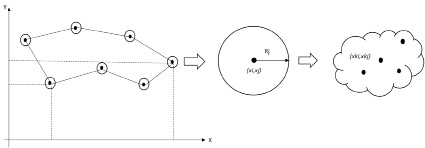
Рис. 3. Распределение точек на координатной плоскости (X;Y), окрестность с постоянным радиусом Rj с координатами (xi,xj), и окрестность случайных n точек, с координатами (xki,xkj), где k – номер окрестности
Для определения координат объектов на плоскости и определения масштаба, в рамках которого проводят расчеты необходимо нанести на карту расположения объектов координатные оси с отложенными на них расстояниями (рис. 2).
В задачах логистики часто приходится иметь дело с вычислением оптимального расположения того или иного объекта.
На первом этапе при выполнении алгоритма поиска центра масс необходимо определится с координатной сеткой и ее масштабом. Для этого изучаемый полигон помещаем в декартову координатную сеть. Для определенности будем исходить из масштаба 1 см. равен 1 км. Каждая вершина полигона находится в некоторой окрестности. Дело в том, что иногда невозможно жестко привязать объект к координатам.
Схематичное представление окрестности координат места расположения объекта со случайным радиусом представлен на рис. 3.
Случайность в определении «центра масс» замкнутого контура (замкнутого графа) или полигона. При определении необходимо учитывать возможность смещения «центра» в пределах некоторой окрестности радиус которой определяется случайной величиной. Случайные величины при решении задачи логистики определения «центра масс» – оптимального расположение распределительного центра.
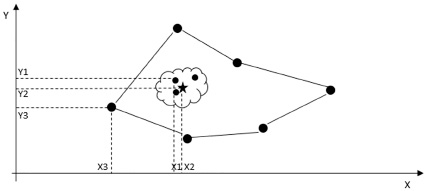
Рис. 4. Схема с координатами геометрического центра (X2, Y2), координат точек объектов распределения ресурсов (X3, Y3), координат точек области – случайных величин группируемых внутри окрестности
Укажем формулы для расчета координат (Xц, Yц) центра распределения классическим способом, формула 1:
Xц =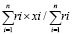 
;
Yц =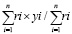 
(1)
Дадим описание пункта 5 алгоритма решения задачи определения центра распределения с учетом того, что координаты анализируемых точек случайные величины. Скорректируем алгоритм вычисления координат центра распределения с учетом случайной составляющей понимая тот факт, что координаты xi, yi есть суть случайные величины. Итак, пусть X и Y – случайные величины, представленные наборами данных X = (x1, x2,…,xn), Y = (y1, y2,…,yn). Также необходимо учитывать, что эти данные в зависимости от влияния внешних и внутренних факторов могут манятся, могут появляется новые точки с новыми координатами и исключаться старые. Так как X и Y увязаны в одну координатную плоскость, то они могут быть связанные между собой функцией, а в случае случайных величин моделью.
Схематически подобная окрестность, включающая координаты, полученные в результате моделирования случайных величин показана на рисунке 4.
С помощью модели могут быть вычислены координаты новых точек в окрестности центра распределения. В случае случайных величин координаты Y связаны c X через модель Ŷ, тогда новая точка в случайной окрестности будет иметь координаты (xi;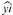
). После этого новые координаты подставляются в формулу 1 для вычисления координат центра распределения. При получении новой информации, новых данных координаты корректируются. Так получается окрестность координат центра распределения, в эту окрестность входят точки, в которых потенциально он может быть размещен.
Результаты исследования и их обсуждение
Учет случайности, внедрение в алгоритм решения задачи специального шага, что усовершенствует решение задачи и позволит сделать алгоритм вычисления координат распределительного центра более универсальным. В случае классического определения координат месторасположения распределительного центра итогом вычислений является точка. На практике же достаточно сложно определить координаты с точность до метров, до десятков метров и т.д. Распределительный центр чаще будет расположен в некоторой окрестности точек. Множество этих точек, их координаты в общем случае случайны и представляют собой варианты координат расположения распределительного центра. В некоторых случаях разброс координат на плоскости может быть существенным. Это связано с точность вычислений, а также с плотностью обозначенных и уже существующих природных и техногенных объектов на исследуемой карте местности. Учтем тот факт, что в некоторых случаях, для конкретных наборов координат размещение распределительного центра на конкретной местности может быть признано невозможным.
Используя такой подход для определения координат распределительного центра, появляется возможность предложить для его местоположения набор координат с учетом влияния различных факторов [5,6]. Например, при изменении формы многоугольника, добавления вершин, появление каких-либо объектов на карте, к которой привязан многоугольник: новых дорог, новых водных объектов, изменение связанные с текущей застройкой, учет влияния последствий чрезвычайных ситуаций и т.п. Все эти факторы и их составляющие приводят к тому, что геометрические координаты распределительного центра будут смещаться случайным образом. В этом случае для определения набора вероятных координат места распределительного центра может быть применен метод статистического моделирования. Именно он призван учесть влияние случайности при определении координат.
Заключение
Во многих экономических задачах часто пренебрегают тем, что данные, которые формируются за счет влияния различных групп факторов и являются по своей природе случайными величинами. Это с одной стороны накладывает на решение задачи дополнительные условия, с другой позволяют сделать подход к ее решению более универсальным. Классическая задача определения местоположения распределительного центра с учетом того, что координаты точек поставщиков ресурсов будут случайными, позволит решить более универсальным способом и определить не только координаты центра, а сформировать целую окрестность наиболее подходящих точек. Формируется несколько вариантов выбора координат для распределительного центра.
Другими словами, необходимо в привязке к конкретной карте местности предложить несколько вариантов размещения центра распределения. Причем некоторые точки окрестности могут быть исключены на первичном этапе обработки, их координаты могут совпасть с уже существующими объектами и расположение центра распределения в этих координатах невозможно. Исключив эти точки и их окрестности, в наборе точек остаются подходящие и их окрестности со случайными радиусами. Из этих точек осуществляется выбор наиболее подходящего места размещения распределительного центра с учетом их случайных окрестностей.
Библиографическая ссылка
Убоженко Е.В., Соловьева Ю.Ю., Вдовин С.А. ОПРЕДЕЛЕНИЕ КООРДИНАТ МЕСТОПОЛОЖЕНИЯ РАСПРЕДЕЛИТЕЛЬНОГО ЦЕНТРА В ЛОГИСТИКЕ С УЧЕТОМ СЛУЧАЙНОЙ СОСТАВЛЯЮЩЕЙ // Вестник Алтайской академии экономики и права. – 2024. – № 3-3. – С. 499-503;URL: https://vaael.ru/ru/article/view?id=3375 (дата обращения: 18.05.2024).