Научный журнал

Вестник Алтайской академии экономики и права

Print ISSN 1818-4057

Online ISSN 2226-3977

Перечень ВАК

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Тинякова В.И. 1 Мирошников Е.В. 2

---

1 ФГБОУ ВО «Российский государственный социальный университет»

2 ФГАОУ ВО «Белгородский государственный национальный исследовательский университет»

Глобализация продолжает усиливать взаимосвязи между национальными рынками, углубляя их интегрированность в единый мировой финансовый рынок. Особо высокой динамичностью отличается рынок ценных бумаг. Именно в этом сегменте финансового рынка можно обнаружить влияние эффектов глобализации на инвестиционные решения. Процесс глобализации формируется множеством достаточно большого числа фондовых рынков и, следовательно, на формальном языке эконометрики, является многофакторным процессом. В то же время воздействие этого многофакторного процесса обладает синергетическим эффектом, который, по сути, и следует считать причиной эффектов глобализации. Предлагаемый авторами статьи подход предусматривает в качестве инструмента, позволяющего реализовать идею построения фактора, в котором в концентрированном виде отражен эффект глобализации, использовать аппарат главных компонент, а для их прогнозирования – процедуру адаптивного моделирования. Представленные в статье расчеты ориентированы на иллюстрацию предлагаемой методики адаптивного моделирования эффектов глобализации в задачах портфельного инвестирования. Прогнозные оценки главных компонент были рассчитаны для индексов, характеризующих среднюю доходность на фондовых рынках Франции (САС40), США (D&J-IND), Англии (FUTESEE-100) и России (RTSSTD). Полученные прогнозные оценки предполагается использовать в качестве факторов в модели прогнозирования доходности финансовых активов, что позволит рассчитать ожидаемые оценки доходности этих активов и уже на основе упреждающей информации построить инвестиционный портфель. Так построенный инвестиционный портфель, по замыслу авторов, будет иметь большую доходность, чем портфель, сформированный по ретроспективным данным.

Статья в формате PDF

481 KB

моделирование

прогнозирование

главные компоненты

биржевой индекс

портфельное инвестирование

1. Прикладная статистика, классификация и снижение размерности / С.А. Айвазян, В.М. Бухштабер, И.С. Енюков, Л.Д. Мешалкин. – М.: Финансы и статистика, 1989. – 607 с.

2. Андерсон Т. Введение в многомерный статистический анализ. – М.: Физматгиз, 1963. – 500 с.

3. Давнис В.В., Бахолдин С.В. Адаптивный подход к обоснованию инвестиционных решений на фондовом рынке // Современная экономика. – 2011. – №5 (17). – С. 146-152.

4. Давнис В.В., Зироян М.А., Комарова Е.В., Тинякова В.И. Прогнозное обоснование инвестиционных решений на финансовых рынках: монография. – М.: Русайнс, 2015. – 220 с.

5. Давнис В.В., Фетисов В.А. Эффекты глобализации и их воздействие на рынок ценных бумаг России // Современная экономика: проблемы и решения. – 2012. – № 12 (36). – С. 145-150.

6. Мирошников Е.В. Моделирование ожидаемых эффектов глобализации в задачах портфельного инвестирования // Современная экономика: проблемы и решения. – 2017. – № 11(95). – С. 8-19.

7. Полякова Е.В., Парфенова В.В Понятие и последствия финансовой глобализации // Актуальные проблемы экономики и менеджмента. – 2017. – № 1(13). – С 55-59.

8. Сорокоумов В.С., Жаркова Ю.С. Глобализация мировых финансовых рынков // Проблемы науки. – 2018. – № 8(32). – С. 38-41.

9. Davnis V.V., Ziroyan M.A., Vladika M.V., Kamyshanchenko E.N., Tinyakova V.I. A situational model of investment portfolio // International Business Management. – 2015. – Т. 9. – № 5. – С. 948-954.

10. Roll R. A Critique of Asset Pricing Theory’s Tests // Journal of Finance and Economics. – 1977. – March. – P. 129-176.

11. Sharpe W.F. A Simplified Model for Portfolio Analysis // Management Science. – 1963. – Vol. 9. – № 2. – P. 277-293.

12. Tinyakova V.I., Maloletko A.N., Kaurova O.V., Vinogradova M.V., Larionova A.A. Model of evaluation of influence of globalization on the national stock market // Contributions to Economics. – 2017. – С. 261-272.

Введение

В настоящее время глобализация стала интегрирующим фактором, который оказывает влияние на развитие и функционирование всех национальных экономик [7]. Прежде всего влияние этого фактора ощущается на фондовых рынках [8]. Поэтому все решения, которые принимают инвесторы должны в своем обосновании учитывать влияние этого фактора.

В тоже время в подавляющем большинстве моделей и методик обоснования инвестиционных решений возможные эффекты глобализацией не учитываются. Естественно, это снижает эффективность принимаемых решений и актуализирует вопрос о внесении соответствующих изменений в модели эффективного рынка.

Глобализация определила новое направление в развитии фондовых рынков. Теперь они не только регулируют эффективное функционирование реального сектора экономики, но и реализует собственную самодостаточность путем создания новых рыночных инструментов, значительным увеличением инвестиционных возможностей и хеджирующих стратегий, а также растущим многообразием всевозможных рисков. Появление новых возможностей и неизвестных ранее рисков ставят перед инвесторами задачи, решение которых требует специальных исследований.

Происходящее под воздействием глобализации объединение финансовых национальных рынков в единый мировой практически завершилось и инвесторы вправе надеяться на то, что рекомендации, которым они следуют в своей инвестиционной деятельности, учитывают этот факт. К сожалению, это не так.

Действие эффектов глобализации диверсифицировано по национальным рынкам. Фактор глобализации формируется, по преимуществу, западными центрами экономики, а эффекты глобализации проявляют себя на национальных рынках. В то же время современная теория портфельного инвестирования в своих моделях не предусматривает механизмы, отражающие эту неоднородность. В первую очередь эта проблема касается самого молодого российского фондового рынка. Поэтому в силу своей актуальности данный вопрос требует проведения научных исследований, которые, безусловно будут востребованы современной практикой инвестиционных решений.

Цель исследования – предложить подход к моделированию прогнозных оценок главных компонент биржевых индексов зарубежных финансовых рынков для получения упреждающих оценок доходности национальных финансовых активов, обеспечивая тем самым учет эффектов глобализации в процессе формирования портфеля ценных бумаг и повышая степень обоснованности инвестиционных решений.

Материал, методы и результаты исследования

Разработанная авторами данной статьи адаптивная модель портфельного инвестирования, отражающая эффекты глобализации [6], имеет ту же самую структуру, что и известная диагональная модель У. Шарпа [11]. Однако смысл символов, с помощью которых записана модель, другой. В них отражена специфика модели, в которой, прежде всего, учтены эффекты глобализации.

Аппарат отражения эффектов глобализации в данной работе основан на использование главных компонент биржевых индексов зарубежных финансовых рынков. Обоснованность использования для этих целей именно главных компонент вытекает из следующих фактов и рассуждений.

Логика и алгоритм построения диагональной модели У. Шарпа предусматривают использование однофакторных регрессионных моделей, описывающих механизм формирования доходности финансовых активов. Не случайно эту модель иногда называют одноиндексной.

По поводу использования для построения данной модели единственного фактора известна так называемая «критика Ролла» [10]. Понятно без дополнительных объяснений, что описать эффект воздействия глобализации с помощью одного фактора, невозможно. Глобализация – это многофакторный процесс. И поэтому, естественно, описание эффектов глобализации должно отражать эту многофакторность.

Компромисс между многофакторной природой глобализации и однофакторным принципом логико-алгоритмической схемы построения модели портфельного инвестирования, предложенной Шарпом, можно достичь с помощью аппарата главных компонент, хорошо описанного в работах [1, 2].

Обычно необходимый компромиссный результат получается при использовании первой главной компоненты, с помощью которой удается наиболее полно отразить совместную вариацию иностранных индексов. Причем, не без основания, можно утверждать, что главная компонента отражает и синергетический эффект глобализации [5]. Во всяком случае вариация, воспроизводимая с помощью первой главной компоненты, значительно превосходит вариацию любого из индексов, которые были использованы для ее формирования. А это является одним из основных признаков, которыми характеризуется синергетический эффект.

Построению главных компонент предшествует процедура предварительной обработки данных. Результаты всех котировок финансовых активов приводятся в стоимостном выражении. Инвесторов, как правило, интересует доходность. Поэтому первым шагом предварительной обработки является расчет доходностей. Если через Sit обозначить стоимость i-го актива, то его доходность в процентах определяется в соответствии со следующим выражением:

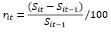. (1)

Доходность финансового актива, как и его цена, является случайной величиной. А это значит, что применение эконометрических моделей требует специального подхода для получения адекватных моделей, с помощью которых можно осуществлять анализ и прогнозные расчеты.

Одним из приемов, который чаще других и не безуспешно используется при эконометрическом моделировании финансовых временных рядов, является процедура скользящего среднего. В результате применения данной процедуры исходный временной ряд превращается во временной ряд с памятью.

Свойства временного рядf с памятью хорошо демонстрирует пример:

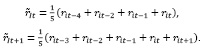
иллюстрирующий отличие двух соседних наблюдений сглаженного ряда. Суммы, из которых сформированы эти наблюдения, отличаются только одним наблюдением. Как правило, такие временные ряды хорошо прогнозируются, что является важным моментом при решении задач портфельного инвестирования.

Здесь уместно заметить, что построение портфеля осуществляется на данных исторического периода, но доход от такого инвестиционного решения является ожидаемым. А наиболее объективной оценкой ожидаемой величины является прогноз. Следовательно, использование временных рядов с памятью, которые хорошо прогнозируются, приводит к значительному повышению надежности инвестиционных решений [4, 9, 12].

Второй положительный результат от применения временных рядов с памятью заключается в том, что переформирование портфеля не осуществляется ежедневно. Поэтому построение портфеля с ориентацией на получение средней доходности за некоторый период находится в полном соответствии с использованием предварительно сглаженных исходных данных.

Построение главных компонент основано на известном методе многомерной математической статистики и практически реализуется с помощью специального программного обеспечения. Главные компоненты были построены для индексов, характеризующих среднюю доходность на фондовых рынках Франции (САС40), США (D&J-IND), Англии (FUTESEE-100) и России (RTSSTD) за период с 04.01.2016 г. по 13.07.2016 г. (табл. 1).

Представленные ниже расчеты, проведенные по данным табл. 1, в основном ориентированы на иллюстрацию предлагаемой методики адаптивного моделирования эффектов глобализации в задачах портфельного инвестирования.

Таблица 1

Динамика биржевых индексов

Принципиальных ограничений на количество учитываемых зарубежных рынков, также как и на количество включаемых в портфель активов, нет.

Методика является универсальным инструментом для решения задач портфельного инвестирования в современных условиях глобализации. Естественно, если расширить количество учитываемых индексов и включаемых в портфель активов, то значительно возрастает только объем вычислений.

Построенные по сглаженным данным главные компоненты могут быть записаны следующим образом:

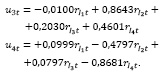
В значениях первой главной компоненты в соответствии с ее весовыми коэффициентами отражено влияние индексов на совокупную вариацию глобализации соответствующих национальных рынков. Самый большой вклад с точностью до знака вносит французский рынок, затем английский, американский и российский. Это позволяет сделать два вывода.

Первый, состоит в том, что происходящие на международных рынках изменения по своей величине превосходят вариации российского рынка, в силу чего должны учитываться при обосновании инвестиционных решений.

Таблица 2

Характеристики вариации главных компонент и индексов

Второй вывод корреспондируется с первым. Его смысл в том, что инвестиционные риски российского рынка ниже инвестиционных рисков иностранных рынков. Во всяком случае на исследуемом промежутке времени это факт.

Для сравнения между собой значения характеристик вариации индексов и главных компонент приведем в виде табл. 2.

Если ориентироваться только на долю вариации, то можно в процедуре дальнейшего моделирования ограничиться применением первой и второй главных компонент. Их совместная доля вариации в общей динамике глобализации занимает 75%.

При построении адаптивной модели портфельного инвестирования главные компоненты используются дважды: при определении упреждающих расчетных значений доходности каждого финансового актива, включаемого в портфель, и при оценке ожидаемого значения этой же доходности. Возникает естественный вопрос о различии между расчетной прогнозной величиной и ожидаемой, которая, по сути, тоже является прогнозной.

Основное различие – в моделях, с помощью которых осуществляется расчет этих величин. Случай, когда эти расчетные величины могут совпасть, не исключается. Но природа этих величин, в данном исследовании, различна. Прогнозная оценка – это результат хотя и адаптивного, но все же детерминированного моделирования с использованием усреднения выборочной совокупности, а ожидаемая – это величина с вероятностной природой возможного своего значения. Но для получения и прогнозного, и ожидаемого значений необходимо иметь упреждающее значение главных компонент, а значит, модель прогнозирования главной компоненты.

Рассмотрим процедуру прогнозирования главных компонент. Сложность данной процедуры в том, что каждая главная компонента формируется из индексов, которые имеют свою собственную динамику, оказывая, с одной стороны, влияние на процесс глобализации, а с другой, – испытывая воздействие глобализации. Поэтому в модели для прогнозирования главной компоненты должны быть учтены и характеристики индивидуального плана, и системные характеристики, отражающие развитие глобального процесса.

Прежде всего при построении такой модели нужно понять принципы отражения собственной динамики и принципы отражения системной динамики. Однозначного понимания этих принципов, скорее всего, нет. Поэтому далее изложим суть своего предложения по построению подобной модели.

Очевидно, что в такой модели должно быть, как минимум, две составляющих, одна из которых отражает изменения в собственной динамике, а вторая – изменения в системной динамике. Собственную динамику проще всего воспроизводить с помощью авторегрессионного процесса первого порядка, модель которого записывается следующим образом:

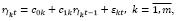(2)

где rIkt – значение k–го индекса в момент времени t; с0k, c1k – оцениваемые коэффициенты авторегрессионной модели; ε_kt – ненаблюдаемая случайная величина, характеризующая ту часть изменения моделируемого показателя, которая не объясняется моделью.

Для воспроизведения системной динамики предлагается использовать косвенные темпы прироста. С помощью косвенных темпов прироста действительно удается отразить согласованность роста моделируемых показателей, но для этого нужно использовать не отдельные модели, а систему взаимосвязанных моделей. Для реализации механизма согласования введем в каждой модели (2) дополнительный член, для чего запаздывающее значение моделируемого показателя представим в следующем виде:

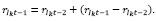(3)

Использование выражения (3) позволяет авторегрессионную модель (2) преобразовать в двухфакторную следующего вида

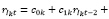
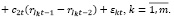(4)

Дополнительный член этой модели предназначен для реализации процедуры, позволяющей осуществить системную сбалансированность прогнозных траекторий. Как уже отмечалось, возможность получения системно сбалансированных прогнозных расчетов основана на использовании косвенных темпов прироста.

Введенный дополнительный член в прогнозные модели позволяет в рамках системы моделей сформировать матрицу косвенных темпов прироста и использовать ее для получения системно сбалансированных прогнозных оценок. Как нетрудно понять, эта возможность реализуема только в рамках всей системы прогнозных моделей. Поэтому все m моделей, после их построения объединяют в одну матричную модель

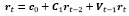, (5)

теоретическое обоснование которой и подробное описание изложено выше. Здесь же мы обсудим практическое использование этой модели на примере данных, с помощью которых иллюстрируется предлагаемая методика адаптивного портфельного моделирования в условиях глобализации.

Сначала выпишем все оцененные двухфакторные модели для каждого индекса

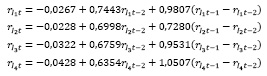
Все характеристики статистической надежности этих моделей приведены в табл. 3.

Таблица 3

Оценки коэффициентов и статистические характеристики надежности авторегрессионно-матричных моделей рыночных индексов

Все коэффициенты моделей, за исключением свободных членов, статистически значимы, а сами модели в соответствии с критерием Фишера адекватны. Относительно статистической незначимости свободных членов у некоторых оцененных регрессионных уравнений, следует дать следующее пояснение. В практике эконометрического моделирования в тех случаях, когда свободный член не значим, а в целом уравнение адекватно, принято допускать использование таких уравнений в практических расчетах.

Изложим детали вычислительного процесса по определению прогнозных значений первых двух компонент. Для записи системы построенных регрессионных уравнений в матричной форме будем использовать следующие данные соответствующие ранее введенным обозначениям, с помощью которых записана модель (5)

Таблица 4

Данные по регрессионным моделям и значениям индексов, необходимые для прогнозных расчетов

Для удобства дальнейшей иллюстрации вычислительного процесса сформируем табл. 4, в которой будут представлены все необходимые для расчетов величины.

Используя данные, приведенные в таблице, проиллюстрируем расчеты, которые были выполнены для формирования матрицы косвенных темпов прироста V. Эта иллюстрация имеет смысл, так как логика процедуры вычисления коэффициентов этой матрицы не совсем очевидна. Ниже приведена последовательность этих расчетов:

Далее определяется обратная матрица

и рассчитывается правая часть выражения

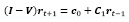(6)

которое получается из (5) для случая, когда осуществляется расчет прогнозного значения.

Таким образом, получены прогнозные оценки всех четырех индексов. С их помощью легко рассчитываются прогнозные значения главных компонент. Имеет смысл рассчитывать прогнозные значения не одной первой, а первой и второй главных компонент, так как они только вместе воспроизводят 75% вариации глобального рынка. Итак, получаем

Заключение

Столь сложный расчет был необходим для того, чтобы прогнозные оценки были системно сбалансированы. Сбалансированность обеспечивалась применением матрицы косвенных темпов прироста, формирование которой осуществлялось по специальному алгоритму, подробное описание которого приведено выше.

Заметим, что сбалансированность – это не искусственно создаваемое с помощью специальной модели свойство рыночных индексов, а естественное направление динамики рынков в глобальной среде их взаимодействия, которое необходимо учитывать для адекватного воспроизведения этих процессов с помощью математических моделей.

Полученные прогнозные оценки главных компонент предполагается использоваться последующих расчетах прогнозных оценок доходности национальных финансовых активов, обеспечивая тем самым учет эффектов глобализации, а значит, повышая степень обоснованности принимаемых инвестиционных решений.

Библиографическая ссылка