Введение
Человечество представляет собой сложную систему, которая постоянно развивается и изменяется. Динамика численности населения каждого региона обладает своей спецификой в силу влияния различных факторов: уровень развития региона, благосостояние населения, болезни и эпидемии, стихийные бедствия. Различные виды математических моделей позволяют выявлять закономерности развития тех или иных демографических процессов, а также служат для анализа состава населения в целом. Развитие теории прогнозирования в последние десятилетия привело к разработке многих методов, процедур и приемов построения прогнозов, различных по своим параметрам [1-3, 5-8, 10, 11, 13-15, 17-19].
К основным моделям численности населения, используемым в демографии, относятся модели стабильного и стационарного населения, экспоненциального и гиперболического роста. Экспоненциальная модель не учитывает факторы окружающей среды и поэтому подходит для малого периода времени прогнозирования. Логистическая модель показывает, что рост численности населения уменьшается по мере того, как население достигает пропускной способности или предельной точки окружающей среды. Широкое распространение имеет логистическая модель с применением уравнения ошибки [2, 6]. Подобная модель также была открыта американским экологом Р.Перлем, в которой отображена зависимость темпов роста от численности населения в конкретный момент и от наличия «неиспользованных резервов жизнеобеспечения населения», например, в виде невозделанных земель. В 1945 г Лесли были предложены матричные модели, в основе которых лежит понятие популяционной системы, описывающей основные взаимосвязи между представителями той или иной группы особей, проживающие на одной территории, имеющие единое происхождение и свободно скрещивающиеся. Матричный способ затрагивает возрастную структуру наблюдаемого объекта. Носовой М.Г. разработана и исследована математическая модель процесса изменения демографической ситуации в виде автономной немарковской системы массового обслуживания с неограниченным числом приборов и РН-распределением времени обслуживания заявок [11].
В работе «A Mathematical and Statistical Approach for Predicting the Population Growth» для прогнозирования численности населения применены модель Мальтуса (простой экспоненциальный рост), логистическая модель и уравнение Ферхюльста, проведено сравнение результатов расчетов трех моделей [1]. Tsoularis A. показал, что наиболее успешные прогностические модели основаны на уравнении логистического роста Ферхюльста, модель простого экспоненциального роста может быть использована для начального периода [13].
В XX веке работы Маккендрика внесли важный вклад в современную экологию и демографию, так с помощью модели эпидемии возможно предсказать количество и распределение случаев инфекционного заболевания [7]. Модели Malthusian, Logistic, Logistic controlled by resources, Biotic interactions, LotkaVolterra, Leslie, Leslie controlled by resources, Ricker, McKendrick проанализированы Rui Dilao с учетом возможности описания вымирания и взрыва популяций, ненулевых состояний равновесия, колебаний, хаоса и квазипериодичности [14].
В работе Иванюка В.А. и Андрейчикова А.В. для полноценного прогнозирования и анализа предложено использовать комбинированную систему нейронная сеть – статистические методы – генетический алгоритм. Генетический алгоритм в данной системе настроен на уборку мусора в данных и выявление наиболее жизнеспособных особей среди данных. Оптимизация и ускорение вычислений в системе способствуют получению наиболее достоверных и точных прогнозов [5].
Основными показателями демографической статистики являются показатели численности и состава населения, количество родившихся, умерших, браков, разводов, миграционного движения. Перечисленные показатели позволяют формировать производные и расчетные показатели, которые способствуют в полном объеме отразить структуру и движение населения, социально-демографические процессы. При анализе социально-экономической ситуации, сложившейся в рассматриваемой территории, численность населения выступает исходным базисным показателем.
Актуальность работы обусловлена необходимостью формирования целостной структуры социально-демографических групп, которые в свою очередь служат основой для формирования социально-экономической политики региона и государства. Для развития национальной экономики, экономического планирования территории и анализа перспектив развития необходима разработка инструментария, позволяющего прогнозировать численность населения региона.
В данном исследовании разработаны модели прогноза численности населения на основе модели Лотки-Вольерры и генетического алгоритма, программно реализованы алгоритмы расчета построенных моделей, проведена оценка точности прогнозирования и получен краткосрочный прогноз численности населения Республики Бурятия.
В качестве исходных данных для прогнозирования численности населения используются показатели рождаемости, смертности и миграции по региону за длительный период. Исследование состоит из двух направлений (рис. 1).
Одним из известных примеров описания динамики взаимодействующих популяций являются уравнения Лотки-Вольтерры, модель взаимодействия двух видов типа «хищник-жертва» (1):
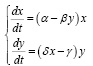 (1)
(1)
где x – число жертв; y – число хищников; t – время; α, β, γ, δ – коэффициенты взаимодействия между видами.
Система уравнений Лотки – Вольтерры находит применение не только в природе, но также часто используется при моделировании экономических систем [17]. Она применима для описания различных процессов в биологии, экологии, медицине, в социальных исследованиях и других науках. Варианты этой модели и сходных с ней применительно к анализу ряда природных и социальных явлений исследованы Д.И. Трубецковым. Так, например, в математической модели взаимодействия загрязнений с окружающей средой в качестве жертвы выступает природа, а в качестве хищника загрязнение. В модели классовой борьбы хищник – земельная рента, жертва – площадь землепользования [18].
В данной работе предложено рассматривать в качестве видов «хищник-жертва» показатели рождаемости, смертности и миграции, так эти показатели попарно являются переменными системы типа (1). Таким образом, построены модели (рис. 2): (differential equations system, DES) Рождаемость-Смертность DES Birth rate-Mortality (DES Br-Mo) (2), Рождаемость-Миграция DES Birth rate-Migraition (DES Br-Mi) (3) и Смертность-Миграция DES Mortality-Migration (DES Mo-Mi) (4). При построении моделей учтена взаимосвязь переменных в каждой паре показателей. Например, в модели Рождаемость-Миграция в первом уравнении коэффициенты при переменных х (рождаемость) и переменной y (миграция) положительные, так как положительный миграционный прирост увеличивает рождаемость.
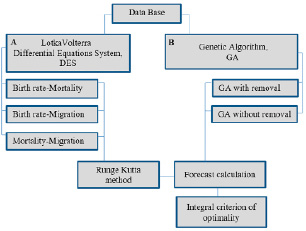
Рис. 1. Схема исследования
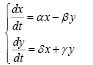 (2)
(2)
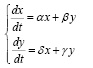 (3)
(3)
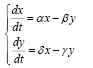 (4)
(4)
Рис. 2. Модели DES рождаемости, смертности и коэффициента миграции
Для решения систем (2-4) использован метода Рунге-Кутта четвертого порядка [12].
В настоящее время для решения задач прогнозирования применяют методы машинного обучения, и одним из его методов, является нейросетевое моделирование. Для обучения и совершенствования нейронных сетей используется генетический алгоритм [3].
Генетический алгоритм (GA) основывается на идее эволюции с помощью естественного отбора и работает с совокупностью особей – популяцией, где каждая особь представляет возможное решение данной проблемы. GA включает в себя следующие этапы: начальная популяция, селекция (отбор), скрещивание (кроссинговер), мутация, формирование нового поколения. Алгоритм повторяется до тех пор, пока будет получен удовлетворительный результат или не произойдет одно из условий: количество поколений (циклов) достигнет заранее выбранного максимума или исчерпано время на мутацию. Основным блоком в GA является блок генетических операторов, который выполняет преобразование популяции альтернативных решений задач оптимизации и искусственного интеллекта [4, 9].
В качестве оператора кроссинговера выбран оператор на основе деления значения пополам и обмена полученных значений между родителями. На этом этапе у двух родителей будет один потомок, за счет повтора результативных значений.
Оператор мутации реализован на основе изменения хромосомы случайным выбором числа из интервала [0,1] для каждой особи и отбором для выполнения этой операции тех особей, для которых случайное число оказывается меньшим значению вероятности мутации.
Следует отметить, что вероятность мутации устанавливается весьма малой (обычно 0 ≤ р ≤ 0.1) и именно от нее зависит, будет данная особь мутировать или нет. Это следует из аналогии с миром живых организмов, где мутации происходят чрезвычайно редко.
Для оценки погрешностей прогнозируемых показателей рассчитаны прогнозы для временных периодов, на которых значения показателей известны. ля прогнозирования показателей демографических процессов исследован GA алгоритм с применением метода удаления лишних особей и без удаления. Входными данными выступали данные за предшествующие 3 или 5 лет прогноза.
Для анализа точности алгоритмов рассчитана площадь под кривой прогнозной функции, вычисленная по методу трапеций для определенного интеграла по каждому показателю [12]. В качестве критерия оптимальности принято отклонение площади прогнозной функции от площади функции реальных значений.
Материалы и методы исследования
Генетический алгоритм и решение модели Лотки Вольтерры методом Рунге-Кутта реализованы на языке С++ в среде разработки Visual Studio 2019. Проведены тестовые расчеты показателей рождаемости, смертности и миграции по данным Республики Бурятия за период 2000-2018 гг. [16]. Расчеты проведены с применением нескольких моделей: Генетический алгоритм без удаления лишних особей GA 1, Генетический алгоритм с удалением лишних особей GA 2, Лотки Вольтерры differential equations system (DES) Рождаемость-Смертность DES Birth rate-Mortality (DES Br-Mo), Рождаемость-Миграция DES Birth rate-Migraition (DES Br-Mi) и Смертность-Миграция DES Mortality-Migration (DES Mo-Mi). Проведена оценка погрешностей прогнозируемых показателей относительно реальных данных.
Прогнозирование на основе модели Лотки Вольтера (DES) в качестве начальных условий взяты значения показателей за предшествующий год. Результаты расчета модели DES Birth rate-Mortality за период 2003-2017 гг. Максимальная погрешность составляет 10,95% для показателя рождаемости и 9,17% для показателя смертности (рис. 3).
Результаты расчета модели DES рождаемости, миграции за период 2003-2017 гг. Для показателя рождаемости максимальное значение погрешности составляет 11,35% и 21,75% для показателя миграции (рис. 4).
Результаты расчета модели DES Mortality-Migration за период 2003-2017 гг. Максимальная погрешность для показателя смертности равна 8,18% и 20,72% для показателя миграции (рис. 5).
Так же проведены расчеты Генетическим алгоритмом без удаления лишних особей GA 1. Показатели рождаемости и смертности варьируются в диапазоне от 0,18% до 15,2%. Показатель миграции имеет значительные отклонения от 0,48% до 28,7% (рис. 6).
Результаты расчета Генетическим алгоритмом с удалением лишних особей GA 2. Погрешности показателей рождаемости и смертности варьируются в диапазоне от 1,12% до 17,36%. Погрешность прогнозирования показателя миграции достаточно велика от 16,82% до 43,27% (рис.7).
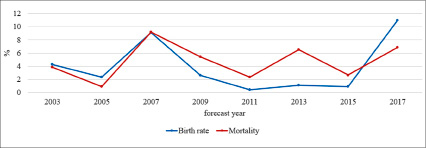
Рис. 3. Значения погрешности DES модели рождаемости, смертности
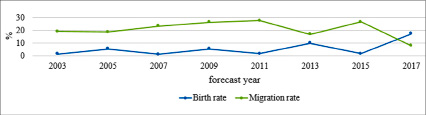
Рис. 4. Значения погрешности DES модели рождаемости, миграции
Рис. 5. Значения погрешности DES модели смертности, миграции
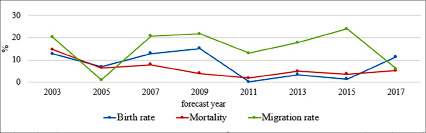
Рис. 6. Значения погрешности GA 1
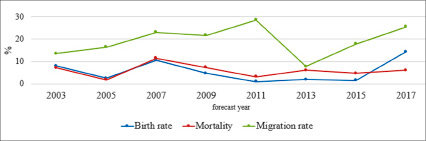
Рис. 7. Значения погрешности GA 2
Результаты прогнозирования позволяют сделать вывод, что применение метода GA 2 дает более точный результат.
Результаты исследования и их обсуждение
Анализ точности алгоритмов
Для анализа точности генетического алгоритма и модели Лотки Вольтерра каждого прогнозируемого показателя методом трапеций вычисляется определенный интеграл [12]. Определяется минимальное отклонение площади прогнозной функции от площади функции реальных значений показателей. Также вычисляется погрешность прогнозирования на каждом шаге расчетов и итоговая средняя погрешность. Результаты оценки точности прогнозных расчетов для двух диапазонов (трехгодичный и пяти годичный) на рис. 8.
Прогнозные расчеты показателя миграции модели GA 2 имеют наименьшее значение отклонения площади для трехлетнего периода 0,58% (средняя погрешность 12,61%) и для пятилетнего периода 5,46% (средняя погрешность 15,97%). Однако, наименьшую среднюю погрешность в пятилетнем периоде имеет модель GA 1 (9.63%). Этот факт позволяет предположить, что процесс пятилетнего прогнозирования показателя миграции с помощью GA 1 содержит точечные пики больших значений погрешности (рис. 9), которые влияют на увеличение площади под расчетной кривой. Таким образом, использование значения отклонения площади позволяет определить резкие скачки расчетных данных.
Демографические данные обладают рядом особенностей: предсказуемость пределов изменений, отсутствие значительных перепадов между ближайшими значениями, временная упорядоченность, зависимость от социально-экономических и политических процессов. Нейросетевое моделирование и машинное обучение позволяют на основе большого числа накопленных данных выявлять закономерности процессов. Но прогнозирования с применением этих технологий необходима предварительная обработка и подготовка данных [6].
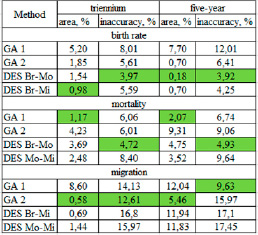
Рис. 8. Результаты точности оценки
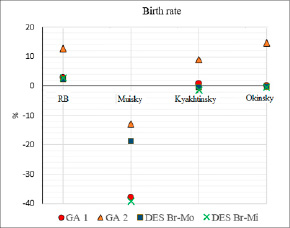
Рис. 9. Ошибка прогноза скорости миграции GA 1 и GA 2
Прогнозные расчеты
По трехлетнему периоду исходных данных (за 2015-2017 гг.) представлены прогнозные расчеты на 2018 год для трех районов Республики Бурятия имеющих различное географическое расположение: Муйский – северный район, Кяхтинский – южный район, Окинский – западный район. Прогноз рассчитан для показателей рождаемости, смертности и миграции по нескольким моделям (рис. 10-12). Показатели рождаемости и смертности для Республики Бурятия и Кяхтинского района прогнозируются практически всеми моделями с достаточной точностью (уровень значимости 0,05). Точность результатов прогнозирования показателя миграции для всех рассматриваемых территорий оказалась более 10 %, можно отметить достаточно кучное расположение погрешностей всех моделей.
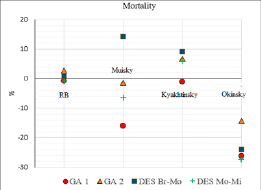
Рис. 10. Ошибка прогноза рождаемости
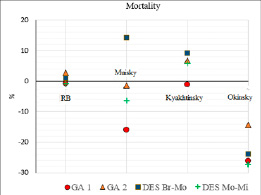
Рис. 11. Ошибка прогноза смертности
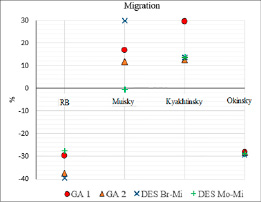
Рис. 12. Ошибка прогноза миграции
Также по результатам расчетов можно сделать вывод об уникальности каждой территории, так для Муйского района погрешности всех моделей имеют отрицательные значения и очевиден разброс значений.
На основе данных за 2016-2018 годы получен прогноза численности населения Республики Бурятия на 2019,2020 и 2021 годы (рис. 13).
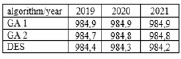
Рис. 13. Прогнозные значения численности населения Республики Бурятия, тыс. чел.
Заключение
Разработка математической модели является основной составляющей моделирования процессов демографического развития территории. В свою очередь, моделирование демографического прогноза является важной частью при формировании демографической политики определенной территории. Выявлена необходимость применения в рассматриваемой области информационных технологий, а именно разработка инструментария для анализа и прогнозирования показателей.
Разработаны и программно реализованы алгоритмы прогнозирования показателей рождаемости, смертности и миграции на основе генетического алгоритма и математической модели в виде системы дифференциальных уравнений. Также произведен анализ показателей и оценка точности алгоритмов. По результатам оценки точности прогнозных расчетов показателей рождаемости, смертности и миграции сделан вывод о том, что для прогнозирования показателя рождаемости лучше применять модель DES, для показателя смертности GA 1 и для миграции GA 2. Выполнен прогнозный расчет численности населения Республики Бурятия на 2021 год.
Библиографическая ссылка
Михайлова С.С., Шулунова И.Р., Балданова М.В. РАЗРАБОТКА МОДЕЛЕЙ, АЛГОРИТМОВ И ПРОГРАММНЫХ СРЕДСТВ ПРОГНОЗИРОВАНИЯ ЧИСЛЕННОСТИ НАСЕЛЕНИЯ РЕГИОНА // Вестник Алтайской академии экономики и права. 2023. № 3. С. 87-96;URL: https://vaael.ru/ru/article/view?id=2745 (дата обращения: 23.02.2026).
DOI: https://doi.org/10.17513/vaael.2745

