Введение
В процессе принятия оптимальных управленческих решений наибольший интерес представляет эффективное решение задач прогнозирования, которое позволяет существенно сэкономить материальные, временные и человеческие ресурсы. При этом методы прогнозирования зачастую основаны на ретроспективных данных о результатах и показателях ведения хозяйственной деятельности экономического субъекта, а точнее на выборке этих показателей за определенный период времени.
Для реализации известных методов прогнозирования исходная информация должна отражать наиболее характерные черты изучаемой совокупности социально-экономических явлений, процессов или показателей, а число наблюдений должно быть достаточно большим [1].
Однако зачастую возникают такие ситуации, когда для выполнения последующего точного прогноза и анализа недостаточно объема данных выборки, но при этом необходимо построить вероятностные высказывания на основе ретроспективных данных. В этом случае используются инструментальные методы виртуального увеличения объема выборки [2].
Целью исследования является разработка методики прогнозирования редких продаж товаров с использованием методов виртуального увеличения статистической выборки на основе модели поведения участников рынка в условиях информационной асимметрии.
Материал и методы исследования
К одному из наиболее популярных и несложных подходов по увеличению объема выборки относится процедура «бутстрэппинга» [2,3], который позволяет строить эмпирическое распределение вероятностей случайных событий, необходимое для оценки точности выборочного параметра с использованием случайного возврата значений из имеющегося набора данных.
При проведении такой процедуры истинное распределение заменяется выборочным, и вместо истинных параметров необходимо использовать данные по полной выборке. Кроме того, полученный расширенный набор случайных значений позволяет более точно проверить разработанную социально-экономическую модель.
Рассмотрим возможности увеличения объема выборки на примере оценки неопределенности объема будущих продаж и экономических рисков в условиях асимметрии информации на рынке.
В качестве примера возьмем рынок новых автомобилей и проанализируем объёмы продаж за определенный период времени. Зачастую автодилеру необходимо выстроить прогноз продаж каждой марки и/или модели автомобиля, к примеру, на два квартала вперед. Для сравнения возьмем три популярных в России модели марки Lada: vesta, granta и largus. Выборка по объемам продаж этих трех моделей с января 2016 г. и по декабрь 2018 г приведена на рисунке 1. На основе этих данных можно рассчитать измерение объема продаж как отношение разности продаж в конце текущего и в конце предыдущего месяца к объему продаж в конце предыдущего месяца.
Для выполнения качественного прогноза необходимо исследовать структуру временного ряда, выбрать трендовую модель, проверить ее на адекватность, исследовать точностные характеристики и т.д. Бутстрэппинг же позволяет без построения прогнозной модели сделать вероятностные высказывания относительно изменения интересующей величины. Рассмотрим, как применяется метод бутстрэппинга для краткосрочного прогнозирования редких продаж с использованием инструментария электронных таблиц [3,4].
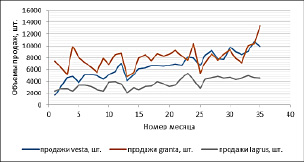
Рис. 1. Объемы продаж новых автомобилей трех марок
Для выполнения качественного прогноза необходимо исследовать структуру временного ряда, выбрать трендовую модель, проверить ее на адекватность, исследовать точностные характеристики и т.д. Бутстрэппинг же позволяет без построения прогнозной модели сделать вероятностные высказывания относительно изменения интересующей величины. Рассмотрим, как применяется метод бутстрэппинга для краткосрочного прогнозирования редких продаж с использованием инструментария электронных таблиц [3,4].
Идея прогнозирования заключается в имитации возможных сценариев поведения кривой продаж, которые берутся из исходного набора данных за 36 месяцев. Причем применение сценария для каждого последующего периода прогнозирования также выбирается из исходного набора. Точкой отсчета для прогноза является значение показателя в конце последнего периода исходных данных. Итак, стоит задача выстроить вероятностные высказывания относительно снижения/роста продаж автомобилей через 2 квартала. Во-первых, необходимо указать начальный объем продаж для каждой модели авто (ячейка N10 на рисунке 2). Во-вторых, смоделировать повторение сценария за месяцы 1-36 в ячейках Q10:Q15. Причем сценарии по месяцам могут повторяться неоднократно. В ячейках R10:R15 указаны сценарии роста или снижения продаж в соответствии с номером месяца из исходной выборки, так, например, во втором месяце (февраль 2016 г.) наблюдался рост продаж модели lada vesta на 79,9% (рисунок 1). Это с связано с выходом данной модели на рынок и повышенным интересом покупателей. Объем продаж в конце указанного периода увеличивается/уменьшается в соответствии с возвращенным из исходной выборки сценарием. Объем продаж в начале следующего периода равен объему продаж в конце предыдущего (рисунок 2а). Таким образом можно определить объем продаж на несколько периодов вперед.
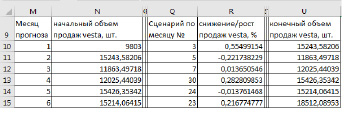
а)
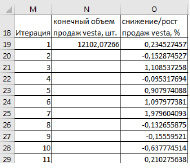
б)
Рис. 2. Модель снижения/роста продаж на 6 периодов в перед (а) и выборка повторения сценариев через 6 месяцев на 1500 значений (часть данных скрыта) (б)
Затем можно непосредственно перейти к самому процессу виртуального увеличения выборки. Для этого необходимо сгенерировать большое количество сценариев объема продаж через 6 месяцев (рисунок 2б). Конечный объем продаж берется на конец 6-го месяца из ячейки U15 на рисунке 2а, и затем для взятого значения прорабатываются 1500 сценариев изменения объема продаж (этого объема достаточно для получения приемлемого уровня точности прогноза). На основании полученного расширенного массива сценариев выполняется анализ статистических показателей и строятся вероятностные высказывания. Например, если необходимо подсчитать вероятность роста продаж, то для этого достаточно из полученного массива на 1500 сценариев подчитать значения снижения/роста продаж, которые больше нуля и поделить на общий объем расширенной выборки (1500 отсчетов). Если брать вероятность реализации любого сценария из выборки за единицу, то полученный показатель, будет отражать вероятность положительного исхода события, т.е. роста продаж и, например, для модели lada vesta будет составлять 74%. При этом в среднем в последующие 6 мес. будет наблюдаться рост продаж данной модели в среднем на 50% с среднеквадратичным отклонением равным 76%. Это означает что вероятнее всего если закупить большую партию автомобилей, то их удачно удастся реализовать, но при этом высока вероятность риска, мерой которого является среднеквадратическое отклонение.
Результаты исследования и их обсуждение
Вероятностные высказывания на основе увеличенной выборки для автомобилей трех марок показаны на рисунке 3.
Из рисунка 3 видно, что большую вероятность положительной динамики продаж показывает модель vesta, при этом у нее же наблюдаются наименьшие показатели уровня вероятности снижения объемов продаж. Не смотря на то что модели granta и largus показывают практически идентичную отрицательную динамику продаж, то в отношении вероятностных высказываний относительно роста продаж, особенно в больших объемах granta показывает лучшие результаты. Это позволяет сделать соответствующие аналитические выводны относительно количества закупаемых у завода под реализацию автомобилей. Следует отметить что все три модели имеют положительную динамику продаж. Однако модель lada largus показывает более стабильные характеристики относительно прогнозных значений продаж (таблица 1), хотя и средний ежемесячный прирост продаж этой модели этой невелик – 1,8%, в отличии от granta – 10,4% и vesta – 53,4%.
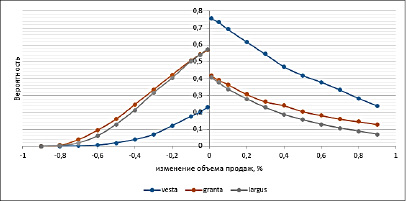
Рис. 3. Вероятность изменения объема продаж для трех моделей авто
Таблица 1
Показатели динамики объема продаж автомобилей
|
Модель авто |
Среднее изменение объема продаж, % |
СКО (мера риска), % |
|
vesta |
0,534 |
0,767 |
|
granta |
0,104 |
0,763 |
|
largus |
0,018 |
0,548 |
Идею бутстрэппинга можно применить также при реализации модели поведения продавцов и покупателей на рынке. Рассмотрим статистику продаж среднего автосалона, который работает на региональном уровне. Кроме него на рынке могут присутствовать несколько автодилеров, предлагающих аналогичную продукцию. Причем в общем случае это могут быть как авто этой же марки, так и аналоги от других производителей, и потребитель в итоге решает для себя какую продукцию выбрать и разумеется главным критерием выбора является соотношение цена/качество. Качество продукта показатель достаточно условный носит интегральный характер, а вот цена является точно измеряемым показателем, который можно смоделировать. И здесь для продавца важно знать оптимальную цену предложения, которая и определяет эффективность продаж.
Построить модель, позволяющую определить оптимальную цену предложения можно на основе метода Монте-Карло [5,6]. Входными данными для модели являются:
– себестоимость продукции для дилера (в нашем случае это отпускная цена завода за автомобиль)
– максимальное количество конкурентных предложений
– вероятность появления конкурентных предложений
– цена предложения дилера за авто. Разумеется, большинство официальных дилеров автомобилей работают по схеме, когда авто предлагается по цене завода, но с дополнительным оборудованием, которое увеличивает его стоимость, поэтому здесь имеется ввиду реальная стоимость, за которую дилер предлагает авто к продаже.
При этом реальное количество конкурентных предложений на рынке, которым отдает предпочтение отдельно взятый покупатель, неизвестно и подчиняется биномиальному закону распределения вероятностей. В модели задается максимальное количество конкурентных предложений, вероятность предпочтения покупателя: этот параметр предполагает, что не всем покупателем нравятся все предложения в городе, обычно они ограничиваются 3-5 предложений из которых выбирают по соотношению цена качество, поэтому данный параметр можно установить на уровне 0,5. Этот показатель по смысловому выражению можно определить, как уровень безразличия предпочтений покупателей, т.е. чем выше это покупатель, тем выше вероятность того, что покупателю для выбора по цене подходит больше конкурентных предложений. Это означает, что, например, из 10 аналогичных предложений средний покупатель выберет 5, которые подходят ему по качеству и дальше будет руководствоваться соображениями стоимости. Выигрышным окажется вариант, который при приемлемом для покупателя уровня качества окажется самым дешевым. Значение критерия α для биномиального распределения позволяет смоделировать случайное поведение покупателей и задается случайным числом с равномерным распределением вероятностей.
Таким образом в каждом отдельном случае проигрывается сценарий поведения покупателя по выбору им автомобиля с устроившими его характеристиками (напомним, что сюда может входить и дополнительное оборудование, подарки, скидки, акции и т.д.) по минимальной цене. Если такой случай произошел, то дилер получает прибыль в размере разности себестоимости и установленной им цены. Если же предложение дилера оказалось не выгодным для покупателя, то дилер не получит прибыли. Теперь остается только понять для какой цены предложения вероятнее всего будет принято решение о покупке авто у интересующего нас дилера с учетом максимального увеличения прибыли. Для этого, как и в предыдущем случае, можно использовать также таблицу сценариев [3,4].
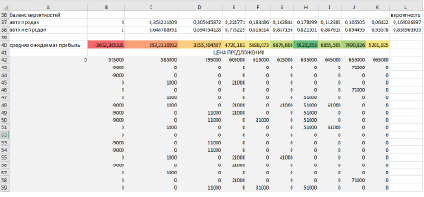
Рис. 4. Таблица сценариев поведения покупателей при разной цене предложения (часть данных скрыта)
На рисунке 4 изображена таблица результатов исхода 1000 сценариев покупки авто при различной цене предложения. При этом наибольшая средняя ожидаемая прибыль в указанном случае соответствует цене предложения 635 тыс. рублей. Данная цена может меняться при изменении условий на рынке. Это может произойти как в результате сговора продавцов, так и в результате появления у покупателей информации о низком качестве товара и т.д. В любом случае такая ситуация приведет к появлению рыночной асимметрии, которая нарушит баланс спроса и предложения на рынке и обеспечит неравномерное распределение между участниками рынка информации об условиях осуществления рыночной сделки и намерениях друг друга. На самом деле такие ситуации часто случаются, их сложно предугадать, но вероятность их появления и степень их влияния на ключевые показатели поведения социально-экономической системы учесть можно.
Рассмотрим пример, когда на рынке появляется больше конкурентных предложений. Так с учетом популярности модели lada vesta в регионе может появиться еще один дилер, который предоставит аналогичный авто к продаже ориентировочно известной нам цене. Это неизбежно приведет к конкурентной борьбе. Если конкурентных предложений будет слишком много, то каждый из дилеров будет терпеть убытки и в итоге кто-то из них уйдет с рынка, что снова приведет его к равновесному состоянию [7,8]. Однако с учетом инерционности социально-экономических систем для этого нужно время. Задача интересующего нас дилера своей ценовой политикой не допустить снижения своих позиций на рынке.
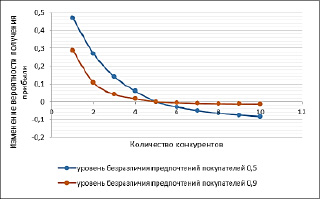
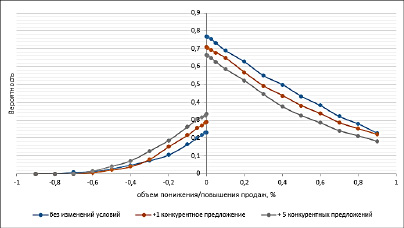
Для решений этой задачи необходимо скорректировать прогноз с учетом изменившихся условий. Это также относится и к рынку авто по всей стране, когда конкурирующий производитель выводит на рынок продукт с аналогичными характеристиками и стоимостью. В этом случае меняется не только количество конкурентных предложений, но и фактор риска [9], определяющий намерения покупателей. В идеальном случае необходимо учитывать условия в которых были получены ретроспективные данные [10,11,12], но это не всегда удается, да и условия внешней среды постоянно изменяются, поэтому для выполнения прогноза достаточно учесть текущие условия на рынке [13]. Пусть сейчас на рынке присутствует 5 конкурентных предложений при этом уровень безразличия предпочтений покупателей равен 0,5. На рисунке 5а. показано как будет изменяться вероятность получения прибыли при изменении количества конкурентов в различных значениях уровня безразличия предпочтений покупателей. Из рисунка 5а видно, что эта вероятность резко изменяется при изменении не только количества предложений на рынке, но и снижении интереса покупателей к конкретному предложению.
а)
б)
Рис. 5. Вероятность получения прибыли при изменении количества конкурентов (а); вероятность получения прибыли при изменении условий на рынке (б)
Выводы или заключение
Таким образом указанные методы позволяют эффективно и точно строить вероятностные высказывания и включать в модель необходимые факторы, в том числе количество конкурентных предложений, которые могут появиться на рынке, а также изменение намерений покупателей относительно выбора подходящего им товара. На основе предложенной модели можно строить оперативные прогнозы не требующие использования сложного инструментария и программного обеспечения. Особенно полезной модель окажется для прогнозирования редких продаж, потому как прогноз только на основе ретроспективных данных при редких продажах будет не столь эффективен, как с использованием данных о состоянии конкурентной среды и намерениях покупателей в условиях информационной асимметрии.
Библиографическая ссылка
Кисляков А.Н. МЕТОД ВИРТУАЛЬНОГО УВЕЛИЧЕНИЯ ВЫБОРКИ ПРИ ПРОГНОЗИРОВАНИИ РЕДКИХ ПРОДАЖ В УСЛОВИЯХ ИНФОРМАЦИОННОЙ АСИММЕТРИИ // Вестник Алтайской академии экономики и права. 2019. № 1-2. С. 47-54;URL: https://vaael.ru/ru/article/view?id=263 (дата обращения: 18.12.2025).

