Введение
В ранних работах одного из авторов и его научного руководителя проф. Халикова М.А. (конкретно, [36,37]) обоснован тезис о преимуществах смешенного финансирования затрат операционного (производственного) сегмента промышленного предприятия корпоративного сектора экономики из собственных и заемных источников с учетом риска структуры рабочего и рассмотрены постановка задачи и математическая модель выбора оптимальной структуры капитала, используемого в покрытии затрат производственной деятельности корпорации (ниже в работе-фирмы) с учетом рисков ее внешней и внутренней сред. В отмеченных работах и в более ранних работах проф. Халикова М.А. и его учеников [1,2,3] как актуальная, теоретически и практически значимая проблема ставилась задача корректной оценки стоимости рабочего капитала, непосредственно влияющая на уровень затрат операционного сегмента и конкурентоспособность фирмы по рентабельности затрат. Также отмечалась актуальность новых знаний в сфере оценки стоимости составляющих пассивов рабочего капитала и, в частности, собственного, в расчетах которого до настоящего времени используется методология и методы, основанные на модели CAPM. Естественно, что для условий современной российской экономики, отличающихся высокой неопределенностью и рисками, необходимы дополнительные исследования теоретического и прикладного характера в направлении уточнения составляющих этой модели и разработки численных методов оценки ее компонент. Решению этой целевой и смежных задач оценки бизнеса и отдельных его сегментов и посвящена настоящая статья.
Материалы и методы исследования
Работа проведена в рамках «неоклассического» подхода, основанного на концепции взаимосвязи эффективности и риска операционного сегмента фирмы, представленной в работах: М.А. Халикова и М.А. Никифоровой [4], А. Минити и Ф. Турино [5], М.А Халикова и М.А. Горского [6].
Широко привлекались работы отечественных и зарубежных исследователей в сферах: оценки и управления стоимостью бизнеса: А.Г. Грязновой.М. Федотовой [7], А. Домодорана [8], Т. Коупленда, Т. Коллера, Д. Муррена [9], Б. Коласса [10]; оценки и управления рисками: М. Круи [11], П. Самуэльсона [12], В. Шарпа и др. [13], А.А. Тимофеевой и И.В. Бурениной [14], Е. Феймы, К. Френча [15], Р. Хамады [16], В. Шарпа [17], Р. Ролла [18], С. Россса [19].
Используемый авторами математический инструментарий методов и численных алгоритмов задач нелинейной (в данном случае, выпуклой) оптимизации и эконометрического моделирования заимствован из работ М.А. Халикова, А. И. Дерябиной, Д. А. Лях и А.М. Антиколь [20,21], Я.Р. Магнуса и др. [22].
В расчетах по приведенным в работе моделям авторы использовали статистическую базу и данные о капитале и рыночной деятельности российских предприятий металлургической отрасли.
Результаты исследования и их обсуждения
1. Модель CAPM и ее критика
Приведем «классический» вариант модели CAPM оценки стоимости собственного капитала компании, предложенной Хамадой (Homada, 1972 г.) [16]:
βL = βu [1 + (1 – t)(D/E)] (1)
где βL – коэффициент бета собственного капитала фирмы с учетом долгового бремени; βu – коэффициент бета фирмы без учета долгового бремени; t – корпоративная налоговая ставка D / E– коэффициент «долг/собственный капитал» (рыночная стоимость).
Коротким ответом на вопрос, является ли CAPM «правильной моделью», является следующий: едва ли мы можем это знать уверено. Проблема- в том, что не известна структура «правильного» рыночного портфеля – все, что мы знаем- лишь приблизительное представление о нем.
Широко известная критика Ролла (1977) [18] показывает, что САРМ не поддается проверке. Поэтому потенциально все проверки могут быть охарактеризованы как несовершенные в тех или иных отношениях.
Одно нз ранних свидетельств показывает, что недиверсифицируемый риск не дает никакой выгоды (что и вытекает из САРМ), и что доход является линейной функцией систематического риска ( как и предсказывала САРМ), хотя известен случай, когда кривая доходов была более плоской и имела более длинный отрезок прямой, чем базовая форма, предсказывавшаяся моделью САРМ.
Более позднее эмпирические исследования САРМ вызвали определенные разногласия. Фейма и Френч заключили, что если учитываются «эффекты масштаба, то «бета» играет незначительную роль в. объяснении сравнительных данных по доходам на акции [15]. Фейма и Френч показали также, что отношение балансовой и рыночной стоимости (BMV) имеет большое значение для объяснения доходов. Это привело к тому, что Wall Street Journal опубликовал даже статью, где говорилось, что фактор «бета» мертв.
Котари, Шенкен и Слоуи (1995) показали, что результаты, полученные Фейма и Фенче в значительной степени зависят от интервала между выплатами доходов, используемого при измерения «беты». Использование годичных интервалов показывает, что «бета» – риск вознаграждается, но что также определенную роль в объяснении доходов играют размеры фирм.
Ким (1995) показал, что главная проблема возникает в том, что коэффициенты «бета» определяются статистически, а следовательно, подвержены ошибкам измерения. тогда как размеры фирм всегда известны точно. Сделав необходимые корректировки, Ким показал, что «бета» важна для объяснения «среза» данных о биржевых доходах в США.
Джаганатан и Вэнг (1996) показали, что если «бета» принимается как фактор экономического риска, а рыночный портфель включает человеческий капитал, то «условная модель CAPM» остается в силе.
Ролл и Росс (1994) [18,19] и Эстон и Типпэт (1998) показали, что оценки «беты» чрезвычайно чувствительны к ошибкам спецификации рыночного портфеля.
Приведенные выше исследования, казалось бы. несут спасение «бете», но проблемы для самого метода САРМ остаются. Проблема «беты» может оказаться неразрешимой, поскольку «бета», как указано выше, чувствительна к недостаткам спецификации действительного рыночного портфеля.
САРМ должен был бы предсказывать все доходы на акции – но представляется очевидным, что на практике существенным дополнительным фактором оказывается различие в размерах фирмы.
Таким образом, нельзя с полной уверенностью утверждать, что модель CAPM является идеальной в своем классе моделй оценки стоимости собственного капитала, она так же имеет свои недостатки, но эта модель позволяет оценить доходность рискового капитала в условиях трансформационных процессов в российской экономике.
2. Направления уточнения модели оценки стоимости привлечения капитала компании
Фирма может привлечь средства из трех источников: собственный капитал, долг и привилегированные акции, следовательно стоимость привлечения капитала определяется как средневзвешанная величина каждого из этих видов издержек. Стоимость привлечения собственного капитала отражает рискованность инвестиции в собственный капитал фирмы, стоимость после уплаты налогов – функция риска дефолта фирмы, а стоимость привилегированых акций есть функция ее промежуточного положения, если судить по риску, между долгом и собственным капиталом. Веса каждого из этих компонентов должны пропорциональным их рыночным стоимостям, поскольку эти пропорции наилучшим образом измеряют то, как финансируется данная фирма.
Выше отмечено, что для оценки стоимости собственного капитала в условиях современной экономики России корректнее использовать модель САРМ (1). Следует отметить, что для ее использования необходимо уточнить методологию вычисления безрисковой ставки, премии и коэффициента бета с учетом специфики трансформационых процессов российской экономики.
Методология оценки собственого капитала Модели риска и доходности в финансах отталкиваются от процентной ставки, доступной инвесторам при безрисковых инвестициях, а также от премии (или премий) за риск, которую инвесторы должны требовать, осуществляя инвестиции при риске, отличном от нулевого. В модели САРМ, где есть только один источник рыночного риска, таковой является премия, которую инвестор запросил бы при инвестировании в этот актив. В многофакторных моделях существует множество премий за риск, каждая из них выражает премию, требуемую инвестором за определенный фактор рыночного риска.
Безрисковая ставка. Актив является безрисковым, если мы с определенностью знаем связанный с ним ожидаемый доход (т. е. фактический доход всегда равен ожидаемому доходу). При каких условиях фактический доход, приходящийся на инвестицию, будет равен ожидаемому доходу? Во-первых, должен отсутствовать риск дефолта. В сущности, это условие исключает любые ценные бумаги, выпущенные частными фирмами, поскольку даже самые крупные и надежные компании в какой-то мере обладают риском дефолта. Единственный вид ценных бумаг с шансом считаться безрисковыми – правительственные ценные бумаги. Правительство вовсе не лучше, чем корпорации, но оно распоряжается печатанием денег, что и является причиной определения таких бумаг, как “безрисковые”. Но крайней мере, хотя бы номинально, правительство должно быть в состоянии выполнить свои обещания. Даже это предположение, каким бы прямолинейным оно ни казалось, не всегда соблюдается, особенно когда правительства отказываются выполнять обязательства, взятые на себя предыдущими режимами, а также в случае заимствования средств в валютах, отличных от национальной денежной единицы.
Существует второе, часто упускаемое из виду условие, которому должны отвечать безрисковые ценные бумаги. Чтобы доход на инвестицию был равен ожидаемому доходу, должен отсутствовать риск реинвестиции. Предположим, что инвестор пытается оценить ожидаемый доход за пятилетний период и безрисковую ставку. Ставка по шестимесячным купонным облигациям, хотя и свободна от риска дефолта, все же не является безрисковой, поскольку существует риск реинвестирования, когда неизвестен размер ставки по облигации через полгода. Даже пятилетние гособлигации не относятся к безрисковым бумагам, поскольку купоны по этим облигациям будут реинвестированы по ставкам, не известным на текущий момент. Безрисковой ставкой для пятилетнего временного горизонта следует считать ожидаемый доход по безрисковой (правительственной) пятилетней облигации с нулевым купоном. Пилотный проект выпуска таких облигаций с аббревиатурой БОБР (Бескупонные облигации Банка России) состоялся в мае 1993 г. Банком России. К сожалению, широкого распространения эти облигации не получили, поэтому в условиях российского рынка не существует инструмента для определения временной структуры безрисковых ставок, которые удовлетворяли бы двум перечисленным выше фундаментальным условиям. Чтобы выйти из этой ситуации можно привлечь к рассмотрению несколько инструментов финансового рынка:
- депозиты Сбербанка РФ и других надежных российских банков;
- ставки по межбанковским кредитам РФ (MIBID, MIBOR, MIACR);
- ставку рефинансирования ЦБ РФ;
- государственные облигации РФ.
Наиболее корректно оценивать безрисковую ставку, исходя из доходности государственных облигаций. На фондовом рынке России обращается несколько видов государственных облиаций :
- ГДО, облигации государственного республиканского внутреннего 30-летнего займа РСФСР. Срок облигаций – с 1 июля 1991 г. по 30 июня 2021 г. Данные облигации обращаются исключительно среди юридических лиц. На торговых площадках не обращаются и не котируются. В расчетах безрисковой ставки использованы быть не могут;
- ОГСЗ, облигации сберегательного займа. Эмитент – Министерство финансов, генеральный агент – Сбербанк РФ. Срок обращения данных ценных бумаг не превышает 1,5 года. Впервые были эмитированы в сентябре 1995 г., эмиссия была возобновлена в 2000 г.;
- ГКО, государственные краткосрочные бескупонные облигации. Эмитент – Министерство финансов РФ. В силу краткосрочного характера использование доходности данного вида ценных бумаг в качестве безрисковой ставки нецелесообразно;
- ОФЗ, облигации федерального займа. Эмитент – Министерство финансов РФ, генеральный агент по обслуживанию выпуска – Центральный Банк РФ. Владельцами данных облигаций могут быть как юридические, так и физические лица, резиденты и нерезиденты. Аукционы и вторичные торги проводятся на ММВБ.
Данный класс облигаций включает финансовые инструменты трех видов: ОФЗ-ПК, ОФЗ-ПД и ОФЗ-ФД.
А) Облигации федерального займа с переменным купоном (ОФЗ-ПК) появились в обращении в июне 1995 г. Процентная ставка купонного дохода рассчитывалась, исходя из доходности по ГКО. В настоящий момент данных ценных бумаг не осталось, их нельзя использовать для расчета безрисковой ставки доходности.
Б) Облигации федерального займа с постоянным купонным доходом (ОФЗ-ПД) впервые были эмитированы в июне 1996 г. для покрытия расходов на компенсацию вкладов в Сбербанке РФ. Срок обращения указанных ценных бумаг составляет от 1 года до 3 лет.
В) Облигации федерального займа с фиксированным купонным доходов (ОФЗ-ФД) появились в январе 1999 г. в результате новации по ГКО после дефолта в августе 1998 г. Срок обращения указанных ценных бумаг составляет 4-5 лет.
На наш взгляд для расчета безрисковой ставки предпочтительнее использовать облигации федерального займа. Эти облигации являются государственными, они номинированы в рублях, что позволяет применить безрисковую ставку к рублевым денежным потокам. Помимо этого на рынке обращаются долгосрочные облигации с датой погашаения вплоть до 2036 г., в следствие чего расчетную безрисковую ставку по ОФЗ можно применять для оценки в долгосрочном периоде. Остальные гособлигации либо номинированы в иностранной валюте, либо являются краткосрочными.
Рассмотрим облигации федерального займа с датой погашения находящейся в промежутке между 2008 и 2036 гг. (таблица 1).
Таблица 1
Облигации федерального займа России
|
Бумага |
Дата |
Дата погашения |
Оборот |
Дох к погаш., эфф. |
Веса |
|
Россия, 25057 |
20.05.2008 |
20.01.2010 |
278123 |
6,11% |
0,0044 |
|
Россия, 25059 |
20.05.2008 |
19.01.2011 |
249985 |
6,24% |
0,0041 |
|
Россия, 25061 |
20.05.2008 |
05.05.2010 |
3977 |
6,26% |
0,0001 |
|
Россия, 25062 |
20.05.2008 |
04.05.2011 |
1976 |
6,39% |
0,0000 |
|
Россия, 26198 |
20.05.2008 |
02.11.2012 |
29341954 |
6,57% |
0,5014 |
|
Россия, 26200 |
20.05.2008 |
17.07.2013 |
99000109 |
6,64% |
1,7098 |
|
Россия, 27026 |
20.05.2008 |
11.03.2009 |
64752580 |
5,82% |
0,9802 |
|
Россия, 46001 |
20.05.2008 |
10.09.2008 |
27954250 |
4,67% |
0,3396 |
|
Россия, 46002 |
20.05.2008 |
08.08.2012 |
54832880 |
6,40% |
0,9128 |
|
Россия, 46003 |
20.05.2008 |
14.07.2010 |
30295950 |
6,00% |
0,4728 |
|
Россия, 46014 |
20.05.2008 |
29.08.2018 |
2110 |
6,61% |
0,0000 |
|
Россия, 46017 |
20.05.2008 |
03.08.2016 |
883405 |
6,55% |
0,0151 |
|
Россия, 46020 |
20.05.2008 |
06.02.2036 |
63332923 |
7,26% |
1,1960 |
|
Россия, 46021 |
20.05.2008 |
08.08.2018 |
13529500 |
6,78% |
0,2386 |
|
Россия, 46014 |
20.05.2008 |
29.08.2018 |
2110 |
6,61% |
0,0000 |
|
Россия, 46017 |
20.05.2008 |
03.08.2016 |
883405 |
6,55% |
0,0151 |
|
Россия, 46020 |
20.05.2008 |
06.02.2036 |
63332923 |
7,26% |
1,1960 |
|
Россия, 46021 |
20.05.2008 |
08.08.2018 |
13529500 |
6,78% |
0,2386 |
Рассчитаем средневзвешанную ставку по ОФЗ с весами, равными доле оборота торгов. Безрисковая ставка составит 6,37%. Эта ставка ниже рассчитанной по депозитам банков с наивысшим кредитным рейтингом, но ниже, чем ставка MIACR, что укладывается в общую канву наших рассуждений.
Премия за риск инвестрования в акции. Мнение о том, что риск имеет значение и более рискованные инвестиции должны обеспечивать повышенную ожидаемую доходность по сравнению с более безопасными инвестициями, кажется понятным на интуитивном уровне. Таким образом, ожидаемый доход на любую инвестицию можно записать как сумму безрисковой ставки и дополнительной доходности, компенсирующей принимаемый риск. Остаются разногласия – как с теоретических, так и с практических позиций относительно того, как измерять этот риск и как обращать его в ожидаемый доход, компенсирующий риск. В данном разделе рассматрим оценку этой премии в модели САРМ.
Модифицированная историческая премия за риск Премию за риск на любом фондовом рынке можно оценить следующим образом [17]:
Премия за риск акций = базовая премия
для зрелого фондового рынка +
+суверенная премия (2)
Суверенная премия отражает дополнительный риск данного рынка. Это предположение сводит проблему оценки к ответу на два вопроса: Какой должна быть базовая премия на зрелом фондовом рынке?
Должна ли в формуле присутствовать суверенная премия, а если да, то как ее оценить?
Для ответа на первый вопрос можно сначала доказать, что фондовый рынок США является зрелым и что есть достаточный объем исторических данных по американскому рынку, чтобы получить приемлемую оценку премии за риск. В действительности, если вернуться к нашему обсуждению исторических премий на рынке США, мы будем использовать среднегеометрическую премию, приносимую казначейскими облигациями и равную 4,71% за период 1928–2007 гг. Мы выбрали столь длительный интервал в целях сокращения стандартной ошибки, согласования существующих казначейских облигаций США с нашим выбором безрисковой ставки, а также с учетом в среднегеометрической премии нашего желания, обусловленного тем, чтобы премию за риск можно было использовать для оценки более долгосрочных ожидаемых доходов.
Следует ли использовать премию за суверенный риск? Являются ли инвестиции в малазийские или бразильские акции более рискованными, чем вложения в американские бумаги? По-видимому, большинство ответило бы на этот вопрос положительно. Тем не менее это еще не дает ответа на вопрос стоит ли использовать дополнительную премию за риск, накладываемую при инвестировании на этих рынках.
Заметим, что единственный риск, имеющий отношение к целям оценки стоимости собственного капитала, – рыночный, который нельзя устранить диверсификацией. В этом случае ключевым становится вопрос о том, является ли риск на российском рынке диверсифицируемым или он не поддается диверсификации. «Средний» российский инвестор размещает денежные средства на внутреннем фондовом рынке и не имеет возможности инвестировать в акции зарубежных компаний, так как это связано с высокими трансакционнымиидержками. Следовательно для него невозможно диверсифицировать рыночный риск. Помимо этого повышение корреляции между рынками привело к тому, что сувеенный риск стал частично недиверсифицируемым.По этой причинемы полагаем, что в условиях российского рынка необходимо использовать премию за страновой риск.
Измерение премий за суверенный риск. Если суверенный риск имеет значение и приводит к более высоким премиям для стран с большим риском, то возникает очевидный вопрос: каким образом измерять эту дополнительную премию.
Известны следующие подходы к измерению премий за суверенный риск:
- спред риска дефолта;
- тносительное стандартное отклонение;
- пред дефолта+относительное стандартное отклонение.
Подход на основе спреда дефолта для облигации и относительного стандартного отклонения цен акций приносят более низкую премию за суверенный риск, чем смешанный поход, когда используются как спред суверенного дефолта по облигации, так и стандартное отклонение по акциям. Мы полагаем, что более значительные премии за суверенный риск, возникающие при использовании смешенного подхода, более реалистичны для условий современной российской экономики, но премии за суверенный риск со временем будут понижаться. Подобно тому, как компании могут стать зрелыми и менее рискованными, страны также могут стать зрелыми и менее рискованными с позиции инвесторов.
Другим аргументом в пользу высказанного тезиса является то,что разница между стандартным отклонением цен акций и облигаций сужается на протяжении более длительных периодов (Джереми Сигел (Jeremy Siegel) приводит данные о стандартных отклонениях на фондовых рынках в монографии Slocks for the Very Long Run, замечая при этом, что они обладают тенденцией снижения со временем).
Таким образом, премия за риск инвестирования в акции будет сходиться со спредом суверенной облигации, когда мы анализируем более долгосрочные ожидаемые доходы.
Спред дефолта + относительное стандартное отклонение. Спред дефолта по стране, согласующийся с рейтингами, измеряет только премию за риск дефолта. Интуитивно можно предположить, что премия за суверенный риск инвестирования в акции будет больше, чем спред риска дефолта по стране. Для рассмотрения вопроса, насколько он будет больше, можно изучить изменчивость национального фондового рынка по отношению к изменчивости суверенных облигаций, используемых для оценки спреда.
Это дает следующую оценку премии за суверенный риск инвестирования в акции:
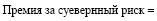
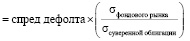 (3)
(3)
В качестве примера рассмотрим Бразилию. В марте 2000 г. Бразилия имела рейтинг, назначенный Moody’s, соответствующий В2, что соответствовало спреду дефолта 4,83%. Стандартное отклонение в годовом выражении бразильского фондового индекса за предыдущий год составляло 30,64%, в то время как стандартное отклонение в годовом выражении для деноминированной в долларах бразильской облигации (C-bond) составило 15,28%.
В итоге премия за суверенный риск инвестирования в акции составила:
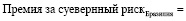
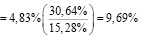 (4)
(4)
Заметим, что премия за суверенный риск повысится, если рейтинг страны падает или в случае повышения относительной изменчивости фондового рынка.
Почему премии за риск инвестирования в акции должны иметь какое бы то ни было отношение к спреду суверенной облигации? Простое объяснение заключается в том, что инвестор, который может заработать 11%, инвестируя в деноминированную в долларах бразильскую государственную облигацию, не согласился бы на ожидаемый доход в 10,5% (в долларовом выражении) от вложения в бразильскую акцию. В действительности, если инвестор желает скорректировать премию за риск облигации, то следует оценить ожидаемый доход на основе ожидаемых денежных потоков с учетом риска дефолта. Следствием будет более низкие спред дефолта и премия за риск инвестирования в акции.
3. Методология уточнения коэффициента бета
Для большинства фирм, акции которых торгуются на открытом рынке, коэффициенты бета могут быть оценены на основе бухгалтерских или рыночных данных, либо на основе восходящего подхода Мы бы почти никогда не стали применять бухгалтерские коэффициенты бета и исторические рыночные коэффициенты бета для отдельных фирм – из-за стандартных ошибок при оценке коэффициента, ошибок в местных индексах (для большинства компаний с формирующихся рынков) и неспособности этих регрессий отразить фундаментальные изменения в комбинации видов деятельности и в финансовом риске фирмы. Наилучшие оценки дают восходящие коэффициенты бета (фундаментальный коэффициент бета) – по причинам:
- позволяют учитывать изменения в комбинации видов деятельности и финансовой сфере компании до моиента осуществления;
- используются средние коэффициенты бета по значительному числу фирм,еоторые имеют меньший уровень шумов, чем коэффициенты бета отдельных фирм;
- позволяют вычислять коэффициенты бета, ориентируясь на сферу бизнеса фирмы, что является полезным в контексте анализа инвестиций и их оценки.
Фундаментальные коэффициенты бета фирмы определяются следующими тремя переменными: 1) вид (или виды) деятельности; 2) уровень операционного рычага; 3) финансовый рычаг.
Вид деятельности (бизнеса). Коэффициент бета измеряет риск фирмы в сопоставлении с рыночным индексом: чем чувствительнее данный вид деятельности к рыночным обстоятельствам, тем выше коэффициент бета. Таким образом, при прочих равных условиях циклические фирмы обычно имеют более высокий коэффициент бета, чем нециклические. Компании, занимающиеся, например, жилищным строительством и производством автомобилей (два весьма чувствительных к экономическим обстоятельствам этих секторов экономики), должны обладать более высокими коэффициентами бета по сравнению с компаниями, занимающимися переработкой пищевых продуктов или табака, которые относительно нечувствительны к деловым циклам.
Данную точку зрения можно распространить и на продукцию компаний. Фирмы, продукция которых не относится к разряду обязательных покупок потребителей (могут отсрочить или отложить покупку данной продукции), должны обладать более высокими коэффициентами бета, чем фирмы, продукция которых считается необходимой. Таким образом, коэффициент бета компании Procter & Gamble, производящей детские памперсы и продукцию повседневного потребления, должен быть ниже, чем коэффициент бета фирмы Gucci, выпускающей предметы роскоши.
Уровень операционного рычага. Уровень операционного рычага является функцией структуры издержек фирмы и обычно выражается соотношением между постоянными и общими издержками. Предполагается, что фирма, имеющая высокие постоянные издержки по сравнению с общими , обладает высоким операционным рычагом. Фирма с высоким операционным рычагом будет отличаться повышенным непостоянством операционного дохода по сравнению с фирмой, выпускающей аналогичную продукцию, но обладающей низким операционным рычагом.
Хотя операционный рычаг влияет на коэффициент бета, его трудно измерить, поскольку постоянные и переменные издержки часто агрегируются в отчетах о прибылях и убытках в одной группе. Приблизительный уровень операционного рычага фирмы можно получить путем анализа изменений в операционном доходе как функции колебания уровня продаж (5):
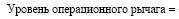
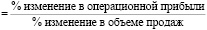
У фирм с высоким операционным рычагом при изменении объема продаж операционная прибыль может изменяться с более ярко выраженной пропорциональностью.
Уровень финансового рычага. При прочих равных условиях урост финансового рычага повысит коэффициент бета собственного капитала фирмы. С интуитивной точки зрения следовало бы ожидать, что фиксированные процентные платежи, возникающие в связи с долгом, приведут к повышению дохода в «хорошие» времена и к снижению – в «плохие». Более значительный финансовый рычаг повышает дисперсию чистой прибыли и делает инвестиции в фирму более рискованными. Если весь риск фирмы возлагается на акционера (т.е. коэффициент бета долга равен нулю) а долг позволяет получить налоговые преимущества, то стоимость собственного капитала оценивается по формуле (1).
Также можно ожидать, что с ростом коэффициента «долг/собственный капитал» инвестор будет подвергаться все большему рыночному риску, приходящемуся на фирму, что отразится более высокими коэффициентами бета.
Коэффициент бета фирмы без учета долгового бремени определяется видами деятельности, фирмы и ее операционным рычагом. Этот коэффициент бета называется «коэффициентом бета активов». Таким образом, коэффициент бета с учетом налогов, который также является коэффициентом бета инвестиций в собственный капитал фирмы, определяется как «рискованность сферы деятельности фирмы» и зависит от уровня риска, связанного с финансовым рычагом.
Финансовый рычаг усиливает базовый риск, связанный с данным видом деятельности. По этой причине предполагается, что фирмы неохотно увеличивают финансовый рычаг. Фирмы, занимающиеся стабильным видом деятельности, в значительно большей степени склонны к повышению доли заемных средств. Например, коммунальные предприятия исторически обладают высокими долговыми коэффициентами, но вовсе не отличаются высокими коэффициентами бета. В основном это обусловлено тем, что их основной вид деятельности стабилен, а результаты предсказуемы.
Восходящие коэффициенты бета. Для развития альтернативного подхода нужно ввести дополнительную характеристику средневзвешенного коэффициента бета совокупности активов, веса которых предлагается определять в соответствии с рыночной стоимостью. Таким образом, коэффициент бета фирмы равен средневзвешенной величине коэффициентов бета, порождаемых видами ее деятельности.
Предлагаемый метод использует численный лгоритм, который включает следующие пять шагов.
1. Определить вид ( виды) деятельности фирмы.
2. Выбрать похожие фирмы, занимающиеся соответствующими видами деятельности, акции которых торгуются на открытом рынке. Получить для них регрессионные коэффициенты бета, которые далее исрлльзуются для вычисления среднего коэффициента бета фирм.
3. Оценить средний коэффициент бета без учета долгового бремени для данного вида деятельности как отношения среднего коэффициента бета фирм и среднего значения коэффициента «долг/собственный капитал». Кроме того, можно оценить коэффициент бета без учета долга для каждой фирмы в отдельности, а затем вычислить средний коэффициент бета без учета долга. Первый подход предпочтительнее, поскольку отношение ошибочно определенного регрессионного коэффициента бета и коэффициента «долг/собственный капитал», по всей вероятности, компенсирует ошибку:
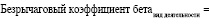
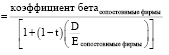 (6)
(6)
4. Оценить коэффициент бета без учета долга для анализируемой фирмы на основе средневзвешенных бездолговых коэффициентов бета для различных видов деятельности, которыми занимается фирма, используя в качестве веса долю стоимости фирмы в каждом сегменте (виде деятельности). Если нет необходимых значений стоимости, то в качестве весов следует использовать операционный доход или выручку. Полученная средневзвешенная величина называется восходящим бездолговым (без-рычаговым) коэффициентом бета (bottom-up unlevered beta):
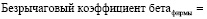
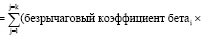
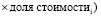 (7)
(7)
В этой формуле предполагается, что фирма участвует в к видах деятельности.
5. Следует оценить текущую рыночную стоимость долга и собственного капитала фирмы, используя коэффициент «долг/ собственный капитал» для оценки коэффициента бета с учетом долга.
На первый взгляд, использование восходящих коэффициентов бета может сохранить проблемы регрессионных коэффициентов бета.. Тем не менее восходящие коэффициенты бета представляют собой значительное усовершенствование по сравнению с регрессионными коэффициентами бета по причинам:
- несмотря на то, что любой регрессионный коэффициент бета оценивается со стандартной ошибкой, среднее из нескольких регрессионных коэффициентов бета имеет значительно более низкую стандартную ошибку. Этот факт объясняется просто. Действительно, если ошибки при оценке коэффициентов бета отдельных фирм не коррелируют между собой, то стандартную ошибку можно представить в виде функции средней стандартной ошибки или оценок коэффициента бета и числа фирм в выборке (8):
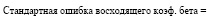

где n – число фирм в выборке;
- восходящий коэффициент бета можно использовать для представления реальных и ожидаемых изменений в комбинации видов деятельности фирмы. Если фирма распродала значительную часть своих операций на прошлой неделе, то веса отдельных видов деятельности должны быть преобразованы для отражения этой распродажи. Также следует обращаться и с приобретениями. Тем самым стратегические планы фирмы по введению новых видов деятельности в будущем могут быть учтены в оценках коэффициентов бета, проводимых для будущих периодов;
- со временем фирмы изменяют долговые коэффициенты. Хотя регрессионные коэффициенты бета отражают средний коэффициент «долг/собственный капитал», наблюдаемый у фирмы в течение периода регрессии, в восходящих коэффициентах бета используется текущий коэффициент «долг/собственный капитал». Если фирма в будущем планирует изменить коэффициент «долг/собственный капитал», то коэффициент бета может быть скорректирован с учетом этих изменений;
- восходящие коэффициенты бета освобождают от зависимости в исторических ценах на акции. Хотя нам по-прежнему нужны цены для получения коэффициентов бета сопоставимых фирм, непосредственно для анализа фирмы нам требуется лишь классификация их видов деятельности.. Таким образом, восходящие коэффициенты бета можно оценить для частных фирм, филиалов и акций, которые только что появились в продаже на финансовом рынке.
Хотя идея, лежащая в основе восходящих коэффициентов бета, довольно проста, есть несколько особенностей приведенного выше алгоритма, заслуживающих внимания:
Определение сопоставимых фирм. Во-первых, нам следует решить, насколько широко или узко мы желаем оценить бизнес. Для примера рассмотрим фирму, которая производит развлекательное программное обеспечение. Мы хотим определить бизнес как «развлекательное программное обеспечение» и рассматривать в качестве сопоставимых фирм только те компании, которые производят в основном такое же программное обеспечение. Но мы можем пойти дальше и считать подходящими для сравнения такие фирмы, которые производят развлекательное программное обеспечение и обладают доходами, аналогичными доходам анализируемой компании. Если этим видом деятельности занимаются сотни фирм, как это наблюдается в секторе программного обеспечения, то можно позволить себе избирательно подходить к формированию выборки. Если существует относительно небольшое число фирм, то потребуется не только стать менее избирательным, но и, вполне вероятно, расширить определение сопоставимых фирм для внесения других фирм в комбинацию.
Оценка коэффициентов бета. После того, как определены сопоставимые фирмы в данном бизнесе, необходимо оценить коэффициенты бета этих фирм. Можно оценить коэффициент бета для каждой из этих фирм в сопоставлении с широким, диверсифицированным индексом акций, предлагается использовать коэффициенты бета для каждой из этих фирм, предоставляемые специализированными службами. Эти коэффициенты бета могут иметь оценку в сопоставлении с различными индексами. Например, если вы относите бизнес к глобальным телекоммуникациям и получаете коэффициенты бета для глобальных телекоммуникационных фирм в агентстве Bloomberg, то эти коэффициенты бета могут быть оценены в сопоставлении с местными индексами. Обычно это не является серьезной проблемой, особенно в случае больших выборок, поскольку ошибки в оценке обычно усредняются.
Метод усреднения. Средний коэффициент бета для фирм в секторе можно вычислить тремя способами. Можно использовать средневзвешенные величины на основе рыночных стоимостей, но снижение стандартной ошибки будет смазано, особенно если в выборке присутствуют одна или несколько крупных фирм. Можно оценить простой средний коэффициент бета компаний, назначая всем коэффициентам бета одинаковые веса. Взвешивание самых небольших фирм в выборке происходит непропорционально их рыночной стоимости, но экономия на стандартной ошибке будет, скорее всего, увеличена.
Учет различий. В сущности, используя коэффициенты бета сопоставимых фирм, мы предполагаем, что все фирмы, которые занимаются определенным видом деятельности, в одинаковой мере подвержены риску, связанному с этим видом деятельности, и имеют одинаковый операционный рычаг. Заметим, что процесс «обременения» и «разгрузки» коэффициентов бета для фирм с долгом позволяет учитывать различия в финансовом рычаге. Если наблюдаются значительные различия в операционном рычаге ( в силу различий в структуре издержек) – они также могут быть учтены. Для этого потребуется оценить коэффициент бета для вида деятельности, где воздействия операционного рычага исследуются на основе безрычагового коэффициента бета:
 (9)
(9)
Отметим здесь схожесть с корректировкой финансового рычага. Единственное различие заключается в том, что посточнные и переменные издержки могут не облагаться налогом, и налоговая ставка, таким образом, больше не рассматривается как фактор воздействия. Коэффициент бета вида деятельности может быть приведен к виду, учитывающему налоги, с целью отразить различия фирм в операционном рычаге.
4. Практические расчеты коэффициента бета с использованием модифицированного алгоритма (на примере ОАО «Полиметалл»).
Стоимость собственного капитала в абсолютном выражении. Стоимость собственного капитала в абсолютном выражении можно найти, перемножив количество акций, выпущенных компаний на рыночную цену: количество акций ОАО «Полиметалл» – 315 000 000шт., средневзвешанная цена торгов за 26.05. 2018 г. на ММВБ составляла 207,81 руб. Стоимость собственного капитала ОАО «Полиметалл» на уквзанную дату составила 31500000х207,81 руб.
Оценка коэффициента бета. Для рассчета восходящего бета коэффицииента будем следовать предложенному вышеалгориму.
1. ОАО «Полиметалл» занимается металлургической деятельностью.
2. Расчет коэффициента бета для акций компании ОАО «Полиметалл» базируется на среднем коэффициенте бета для отрасли компания (металлургия). Рассмотрены тринадцать компаний: Магнитагорский металлургический комбинат (ММК), Новолипецкий металлургический комбинат (НЛМК), ВСМПО-АВИСМА, ГМК Норникель, Полюс Золото, Ашинский металлургический завод, ВМЗ.
Для каждой из компаний рассчитан коэффициент бета, исходя из исторических данных за 2015-2018 гг.(представлены на сайтах [23-35]). В качастве индекса фондового рынка использовали значения индекса ММВБ за соответствующие даты. Чтобы избежать проблемы неликвидности торгов, по некоторым акциям было решено использовать месячные интервалы. Также для расчетов необходимы значения заемного и собственного капитала и операционного рычага (таблица 2). По этим данным необходимо расчитать средние значения по отрасли. Результаты вычислений представлены в таблице 3.
Таблица 2
Сводные данные по компаниям метаооургической отрасли [23-35]
|
Компания |
Коэффициент Бета |
коэффициент «долг/собственный капитал» (%) |
Налоговая ставка |
Фиксированные/ переменные издержки (%) |
|
ММК |
0,37 |
30,77% |
24,00% |
53,69% |
|
НЛМК |
0,91 |
7,43% |
24,00% |
78,50% |
|
Северсталь |
0,68 |
17,74% |
24,00% |
28,26% |
|
ВСМПО-АВИСМА |
0,26 |
39,67% |
24,00% |
112,18% |
|
ГМК Норникель |
1,09 |
36,40% |
24,00% |
45,21% |
|
Полюс Золото |
0,74 |
0,24% |
24,00% |
20,80% |
|
Ашинский |
1,10 |
29,32% |
24,00% |
19,16% |
|
Выксунский |
0,80 |
100,36% |
24,00% |
37,79% |
|
Мечел |
1,41 |
29,50% |
24,00% |
8,77% |
|
Первоуральский НТЗ |
0,67 |
53,62% |
24,00% |
32,84% |
|
Челябинский цинкзавод |
0,42 |
58,65% |
24,00% |
8,67% |
|
Синарский трубный |
0,84 |
47,34% |
24,00% |
15,91% |
|
Гайский ГОК |
0,79 |
54,26% |
24,00% |
11,69% |
|
Средняя величина (прстая) |
0,78 |
38,87% |
24,00% |
36,42% |
|
ОАО Полиметалл |
0,65 |
63,07% |
24,00% |
27,10% |
Таблица 3
Статистические данные регрессионных моделей для компаний металлургической отрасли
|
ММК |
НЛМК |
Север-сталь |
ВСМПО- АВИСМА |
ГМК Норникель |
Поли-металл |
Полюс Золото |
Ашинский |
Выксунский |
Мечел |
Перво-уральский НТЗ |
Челябинский ТПЗ |
Синарский трубный |
Гайский ГОК |
|
|
Параметр а |
0,0010 |
0,0011 |
0,0006 |
-0,0002 |
0,0003 |
-0,0001 |
-0,0007 |
-0,0029 |
0,0310 |
0,0535 |
0,0390 |
0,0047 |
0,0490 |
0,0298 |
|
Параметр бета |
0,3738 |
0,9092 |
0,6761 |
0,2580 |
1,0945 |
0,6538 |
0,7385 |
1,1035 |
0,7994 |
1,4101 |
0,6735 |
0,4234 |
0,8359 |
0,7896 |
|
Статистика вариации |
||||||||||||||
|
Стандартное отклонение фондового рынка |
0,0008 |
0,0007 |
0,0005 |
0,0003 |
0,0007 |
0,0005 |
0,0005 |
0,0331 |
0,0079 |
0,0701 |
0,0167 |
0,0575 |
0,0715 |
0,0204 |
|
Стандартное отклонение акции |
0,0004 |
0,0004 |
0,0004 |
0,0004 |
0,0004 |
0,0003 |
0,0004 |
0,0044 |
0,0044 |
0,0047 |
0,0044 |
0,0044 |
0,0037 |
0,0044 |
|
Систематическая вариация |
0,0001 |
0,0003 |
0,0002 |
0,0000 |
0,0005 |
0,0001 |
0,0002 |
0,0053 |
0,0028 |
0,0094 |
0,0020 |
0,0008 |
0,0026 |
0,0027 |
|
Несистематическая вариация |
0,0008 |
0,0004 |
0,0003 |
0,0003 |
0,0002 |
0,0004 |
0,0003 |
0,0278 |
0,0051 |
0,0607 |
0,0147 |
0,0567 |
0,0689 |
0,0176 |
|
R-квадрат |
6,77% |
44,97% |
35,47% |
7,79% |
68,38% |
22,44% |
45,30% |
16,04% |
35,53% |
13,38% |
11,85% |
1,37% |
3,63% |
13,43% |
2. По формуле (6) найдем безрычаговый коэффициент бета для отрасли:
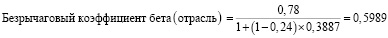 (10)
(10)
Пересчитаем этот коэффциент с учетом операционного рычага:
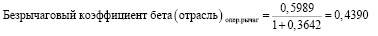 (11)
(11)
4. По формуле (7) найдем восходящий бездолговой (безрычаговый) коэффициент бета для ОАО «Полиметалл»:
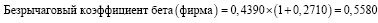 (12)
(12)
5. Рассчитаем рычаговый (восходящий) коэффициент бета для ОАО «Полиметалл»:
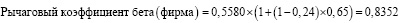 (13)
(13)
По формуле (1) рассчитаем стоимость собственного капитала компании ОАО «Полиметалл» на конец 2018 г.:
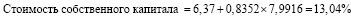 (14)
(14)
Следует подчеркнуть, что обслуживание собственного капитала по ставке 13,04%-весьма удовлетворительный для российской металлургической отрасли показатель, демонстрирующий наличие перспектив роста конкурентоспособности оцениваемой фирмы по затратам в условиях возможности привлечения с финансового рынка «недорогих» кредитов и повышения гибкости производства.
В заключении отметим, что основная цель исследования, заключавшаяся в анализе практики применения в российской экономике и выбора направлений модернизации методологии CAPM с учетом российских реалий, достигнута: предложен пятишаговый апгоритм оценки стоимости собственного капитала производственной корпорации с учетом восходящего бета-коэффициента и проведено его тестирование на примере компании металлургической отрасли. Предложенный метод позволяет повысить точность оценок стоимости составляющих капитала компании и качество принимаемых на их основе решений по управлению ее денежными потоками.
Библиографическая ссылка
Аббясова Д.Р., Воротникова Д.В., Струкова А.А. СОВРЕМЕННОЕ СОСТОЯНИЕ ПРОБЛЕМАТИКИ ОЦЕНКИ СТОИМОСТИ СОБСТВЕННОГО КАПИТАЛА КОРПОРАЦИИ И НАПРАВЛЕНИЯ СОВЕРШЕНСТВОВАНИЯ МОДЕЛИ CAPM // Вестник Алтайской академии экономики и права. 2022. № 9-1. С. 5-18;URL: https://vaael.ru/ru/article/view?id=2385 (дата обращения: 11.02.2026).
DOI: https://doi.org/10.17513/vaael.2385

